疊層板狀結構的非線性振動特性分析★
付 超
0 引言
工程實際中存在著大量的流固耦合振動現(xiàn)象,是設計和應用時必須考慮的重要因素。流固耦合力學的重要特征就是固—液兩相介質之間的交互作用,并通過其耦合面的變形和協(xié)調關系體現(xiàn)于控制方程中。
1 模型的建立
核反應堆中的疊層板元件是由多層薄窄板疊合而成,相鄰板間一般僅有毫米級的間隙供冷卻劑流過。本文采用一個置于剛性矩形槽的兩端簡支板狀結構模型進行模擬,并在板的中間位置設置彈簧支承。如圖1所示,板只在xoz平面內振動。
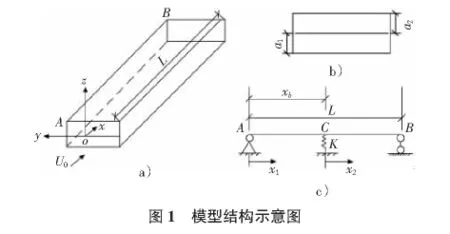
流體以平均流速U0,從A端流入,B端流出。并假設:
2)各板在流場中自由振動時橫向振型完全相同;
3)流體為x和z方向流動的二維不可壓縮無粘性流體。
2 理論分析
若假定各板具有相同的相位和振幅,根據(jù)經(jīng)典小薄板彈性理論可得到流體動壓力的表達式:
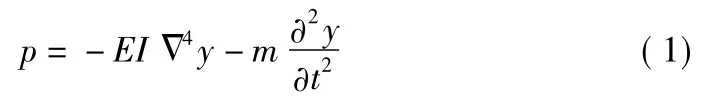
其中,EI為單塊板的抗彎剛度;y為板的橫向位移;m為單位面積上板的質量;p為板上、下表面的壓力差。
考慮勢流理論,流致振動的運動方程可表示為:
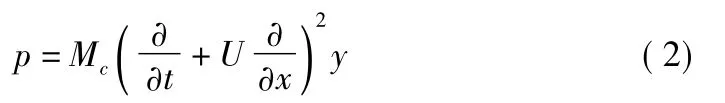
其中,Mc為流道內流體單位長度的質量;U為流體沿疊層板狀結構長度方向的流速。
將式(2)代入式(1),流致振動控制方程可表示為:
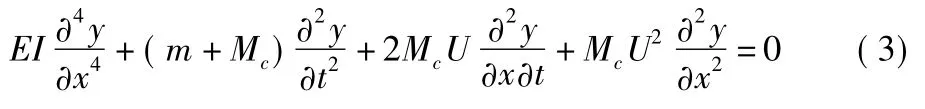
受振蕩流的影響,假定速度U為:
面對市場環(huán)境和消費趨勢的變化,海爾廚電積極整合斐雪派克等全球頂級品牌資源,以智慧大成套解決方案豐富海爾系廚電的內涵,引領世界廚電產(chǎn)業(yè)發(fā)展趨勢。目前,海爾系廚電已擁有煙、灶、消、烤、蒸、微波爐、咖啡機、廚凈寶、冰箱、洗碗機、酒柜11大品類,在2018年廚電市場整體下滑的態(tài)勢下,海爾系廚電截止至11月集體實現(xiàn)逆勢增長,背后源于海爾廚電以用戶為中心的開放生態(tài)體系。

其中,ε為微小量;v為頻率參數(shù)。
在板的中間支承處添加彈簧支承,并考慮阻尼系數(shù)的影響,則板狀結構的流致振動控制方程為:
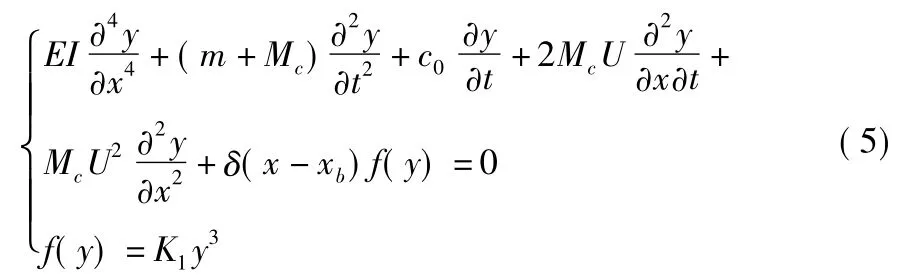
其中,EI為板的抗彎剛度;m為板的單位長度質量;c0為結構阻尼系數(shù);δ為DIRAC函數(shù);K0為彈簧的線性剛度系數(shù);K1為非線性剛度系數(shù);y為板的共同振幅。運用RITZ-GALERKIN離散化方法,將式(5)離散化,可假設:
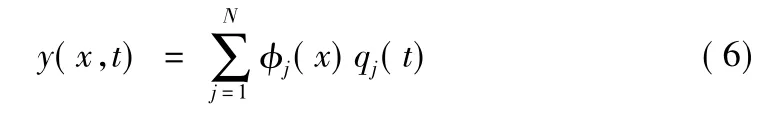
其中,φj(x)=Asin(jЛ/L)
考慮模態(tài)的對稱與反對稱性,取兩個自由度,即N=2。將式(6)代入式(5),再利用主振型的正交性,在方程兩邊同時乘以φj(x)=Asin(jЛ/L),j=1,2,并沿板長取(0,L)進行積分,將式(4)代入方程,整理得到:
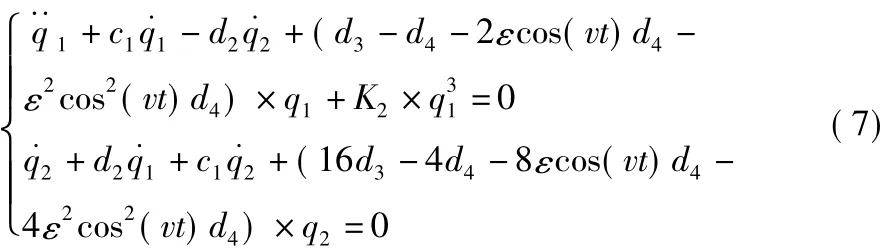
其中,d1=m+Mc;c1=c0/d1;d2=16McU/(3Ld1);d3=EIЛ4/(L4d1);K2=2K1/(Ld1);d4=McU20Л2/(L2d1)。當結構阻尼和剛度系數(shù)較小時,可設:c1=ε×c,K2=ε×K3。
根據(jù)多尺度理論方法,首先假設考慮基本參數(shù)共振:
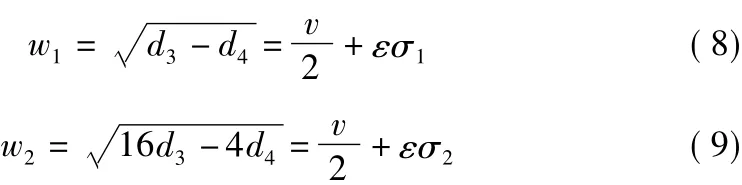
其中,σ為調諧參數(shù),只取一階近似值。令T0=t,T1=εt,并同時引進算子:
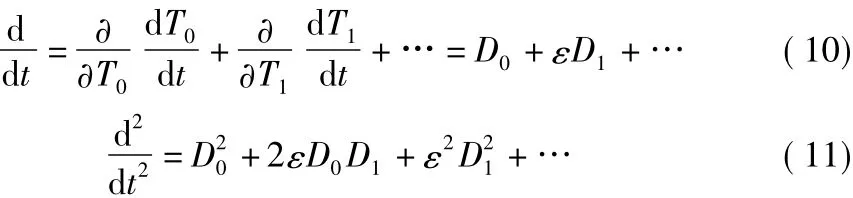
將式(8)~式(11)的關系方程代入式(7),整理并消去違背保守系統(tǒng)機械能守恒的物理定律的永年項后,得到自治微分方程:
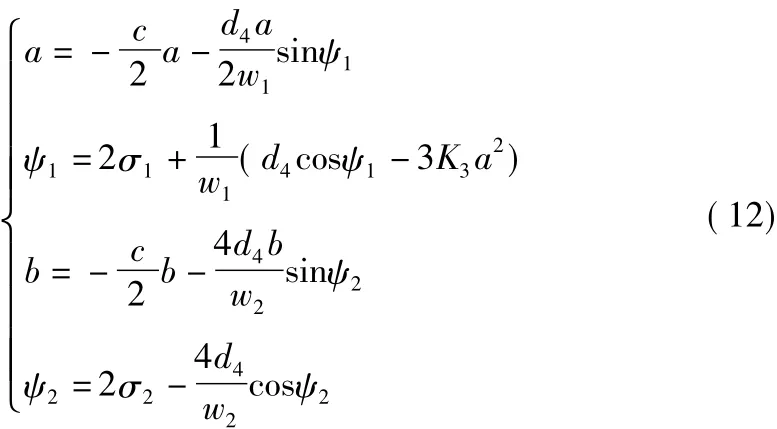
由式(12)可見,非線性剛度項沒有直接作用在振幅上,而是通過相位間接影響振幅。另若假定a=ψ1=b=ψ2=0,可得其一階振幅的定常解為:

式(13)中由于幅值必須是一個大于零的實數(shù),只需考慮振幅a滿足條件,即要求 d24≥c2ω21。即:ε≥c1ω1/d4,并且得到式(13)的非零解:

令E=εσ1=v/2-ω1,E為一階振動的頻率差,表示激勵頻率的1/2與線性頻率的差。則式(13)變?yōu)?
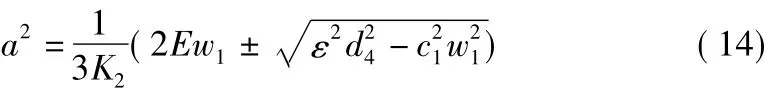
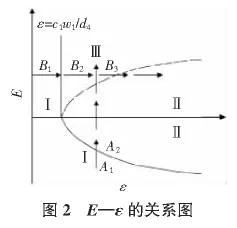
由式(14)可知,當a=0時,得:

另外,由式(15)可看出,當系統(tǒng)共振時,即各階模態(tài)不存在相位差(E=0)時,振幅a與微量ε和參數(shù)d4成正比,與頻率參數(shù)v和參數(shù) c1成反比,其中 d4=Mc2/(L2d1),c1=c0/(m+Mc);若取Mc/(m+Mc)為質量比,則振幅a還與質量比、流速U0成正比關系,而與阻尼系數(shù)c0、板長L成反比;且振幅隨相位差E的增大而不斷增大。
3 結語
1)利用多尺度的分析方法,發(fā)現(xiàn)非線性剛度對振幅的影響,體現(xiàn)為通過相位間接的影響振幅。
2)系統(tǒng)共振時,即各階模態(tài)間不存在相位差(E=0)時;振幅a與微量ε、參數(shù)d4、質量比和流速U0成正比,而與頻率參數(shù)v和參數(shù)c1、阻尼系數(shù)c0以及板長L成反比;且振幅a隨相位差E的增大而不斷增加。
[1]Guo C Q,Paidoussis M P.Stability of Rectangular Plates with Free Side-Edges in Two-Dimensional Inviscid Channel Flow[J].Journal of Applied Mechanics,2000,67(1):171-176.
[2]Guo C Q,Paidoussis M P.Analysis of Hydroelastic Instabilities of Rectangular Parallel-Plate Assemblies[J].Journal of Pressure Vessel Technology,2000(122):502-508.
[3]陳貴清,楊翊仁.振蕩流作用下的非線性板狀梁結構參數(shù)共振研究[J].西南交通大學學報,2002,37(sup):18-22.
[4]王 琳.流動壓力作用下板狀疊層結構的分岔和混沌[J].動力學與控制學報,2006,4(1):93-96.
[5]陳貴清,楊翊仁.受非線性支承的板狀梁結構流致振動研究[J].固體力學學報,2003,24(3):108-117.
[6]張鳳翔,陳貴清.板狀結構流致振動的研究[J].振動與沖擊,2004,23(2):11-15.
[7]郭長青.疊層板型元件模型干模態(tài)固有頻率與振型分析[J].中南工學院,1995(6):17-23.

