FP-SSA框架中Au3Cu型有序合金相的特征原子勢能配分函數

謝佑卿 ，聶耀莊，李小波，劉心筆 ，彭紅建，李艷芬

(1. 中南大學 材料科學與研究工程學院，長沙 410083；2. 中南大學 粉末冶金國家重點實驗室，長沙 410083；3. 中南大學 物理科學與技術學院，長沙 410083；4. 湘潭大學 機械工程學院，湘潭 411105；5. 中南大學 化學化工學院，長沙 410083)

依據一般系統科學的3個哲學命題，建立了系統合金科學(SSA)框架。這3個命題是：1)任何一個系統中其結構的多樣性歸因于結構單元序列中結構單元的組合和排列；2)系統的性質多樣性歸因于結構單元之間的相互作用內容和方式；3)多組元系統的復雜性和整體性歸因于結構和性質的多層次性，不同結構層次之間的相關性以及系統與環境合一的開放性。

SSA框架包含兩部分：SSA理論框架和合金特征原子排列設計應用工程。SSA理論框架分為兩個分支：以第一原理(FP)——合金電子理論和以實驗測量技術(EX)為基礎的SSA理論框架。它包含6個彼此相關聯的層次理論(見圖1)[1]，它們之間的關系用結構單元序列鏈、公式鏈和信息鏈描述。其目的之一是闡明合金系統3個結構層次的結構和性質的多樣性。這3個結構層次是：1)組織結構，組成單元為相；2)合金相結構，組成單元為原子；3)合金相中原子的電子結構，組成單元為電子和原子核。

合金相是組元原子在基本點陣中排列的溶體。發展 SSA框架中的合金相溶體理論就是要按照系統科學的3個哲學命題在相應的3個方面創新，建立配分函數，然后導出系列公式，如Gibbs能函數等。對于單相j的溶體，有

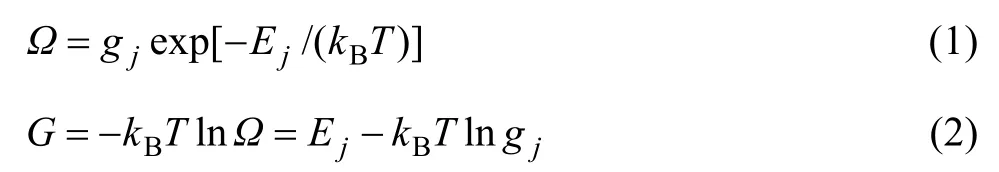
式中：?為勢能配分函數；gj為原子排列簡并因數；Ej為合金能量狀態；kB為Baltzman常數；T為熱力學溫度；G為Gibbs自由能。

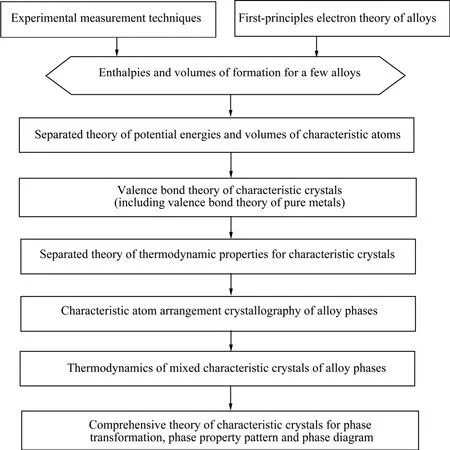
圖1 以實驗技術和第一原理金屬間化合物電子理論為基礎的SSA理論框架的層次理論Fig.1 Theoretical levels of SSA framework based on experimental measurement techniques and first principle electron theory of alloys

這3個方面是：1) 尋找能夠闡明合金相結構多樣性的結構單元序列，建立結構模型；2) 選擇能量相互作用方式，確定組元(α)的結構單元能級()和相應的原子濃度()；3)建立與合金相能量狀態Ej(Ej=相應的原子排列簡并因數gj和熵的計算方法。

配分函數是相結構層次公式鏈中的基本函數。CAPE配分函數的建立，不僅能為建立特征原子Gibbs能配分函數奠定基礎，而且能揭示當今流行的相圖計算(CALPHAD)評估[2]和它與原子集團變分法(CVM)[3]結合的 CALPHD-CVM 理論[4]以及 FP-電子結構計算與CVM法結合的FP-CVM理論[5]的不足之處。它們是過去20多年來正在形成的新方向，這是因為在高溫下組態熵對合金相的Gibbs能起重要作用[6]。

本文作者將以 Au3Cu型有序合金為例，介紹CAPE配分函數、特征原子濃度分布函數、特征原子勢能分布函數以及與特征原子能級相應的原子排列簡并因數，計算合金相及其組元的平均原子勢能、摩爾生成焓和摩爾組態熵。

1 結構單元和結構單元的勢能能級

在FCC基本格子Au-Cu系中，每個原子受最近鄰配位原子團 [( I - i )Au,i Cu]包圍，這里，i是Cu原子數，(I?i)是Au原子數，I是配位數，其值等于12。因此， 能夠描述合金相中原子空間排列的幾何特征和原子之間相互作用方式的結構單元是基本原子團和

在L12-Au3Cu化合物中，每個Au原子(稱為特征原子)由配位原子團[8Au, 4Cu]包圍，每個Cu原子(稱之為特征原子)由配位原子團[12Au, 0Cu]包圍。L12-Au3Cu的FCC基本格子由兩個亞點陣組合形成，一個由原子占據，另一個由原子占據(見圖2)。當L12-Au3Cu變成Au0.75Cu0.25無序合金時，基本原子團={·[8Au, 4Cu]}和{·[12Au, 0Cu]}分裂成為和序列。由于配位原子團[8Au,4Cu]和[12Au, 0Cu]分裂成配位原子團 [( I -i )Au, iC u]序列，導致作用于和特征原子的勢場發生變化；特征原子和分裂成和特征原子序列，它們的勢能和分裂成和序列，體積和分裂成和序列。

根據這一分析, 本文作者提出了闡明合金相結構和性質多樣性的3個相互關聯的模型[7?11]：1) 基本原子團交疊(BCO)模型，合金相由基本原子團交疊形成，其結構單元為一對基本原子團和序列；2)特征原子排列(CAA)模型，合金相由特征原子排列形成，其結構單元為一對特征原子和序列；3)特征晶體混合(CCM)模型，合金相由特征晶體混合形成，其結構單元是特征原子組成的和序列。此模型是緣于以下啟示提出的：純金屬FCC-Au和FCC-Cu是Au-Cu系中的子系統，它們分別由Au-Cu系中特征原子和排列形成的特征晶體和。因此，13種和特征原子可分別形成13種虛擬的特征晶體和13種虛擬的特征晶體。

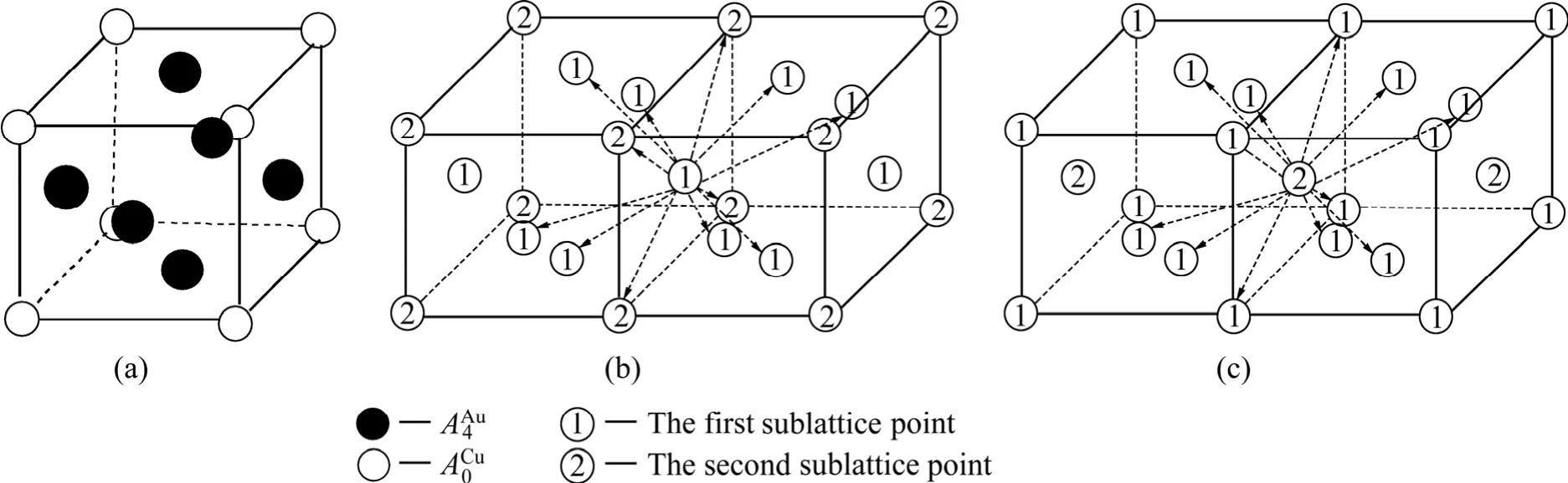
圖2 L12-Au3Cu化合物特征原子排列晶體結構、以第一類亞格點為中心的最近鄰配位格點及以第二類亞格點為中心的最近鄰配位格點Fig.2 Characteristic atom occupation structure of L12-Au3Cu compound (a), the first and second sublattice points in coordinative cluster surrounding the first sublattice point (b), and the first and second sublattice points in coordinative cluster surrounding the second sublattice point (c)

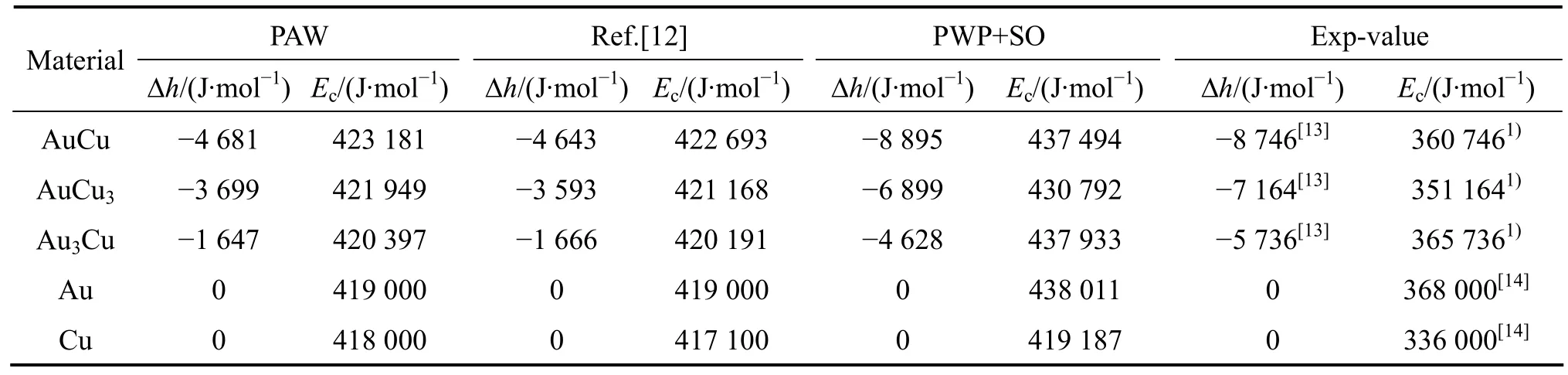
表1 0 K時采用第一原理計算的L10-AuCu、L12-Au3Cu和L12-AuCu3化合物以及純Au和純Cu的生成焓、結合能及其實驗值Table 1 Heats of formation (Δh)and cohesive energies (Ec)of L10-AuCu, L12-Au3Cu and L12-AuCu3 compounds, Au, and Cu metals at 0 K calculated by FP-electron theory and measured by experimental techniques

表2 合金的平均原子勢能函數Table 2 Average atomic potential energy functions of alloy phases

1) 直線關系(Ⅰ型)

2) 凹型拋物線關系(Ⅱ型)

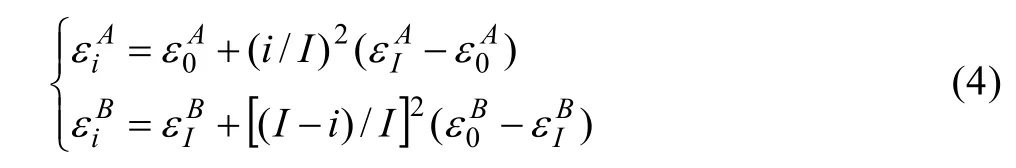
3) 凸型拋物線關系(Ⅲ型)

按以下步驟分離出Au-Cu系中特征原子勢能：

1) 采用結構單元反算法，應用9個ε(x, 0, )σ函數從第一原理計算的L10-AuCu、L12-Au3Cu和L12-AuCu3化合物以及純Au和純Cu的總勢能中分離出特征原子勢能。

2) 由9個ε(x, 0, )σ函數和相應的特征原子勢能計算最大有序度Au3Cu、AuCu和Au3Cu型有序合金，無序合金的生成焓，以及它們的差值(即過剩勢能)。

3) 在不考慮振動對焓和熵的貢獻，且假設合金的最大有序度(計算公式見第 3節)不隨溫度變化的情況下，由式(6)計算有序?無序轉變臨界溫度Tc：

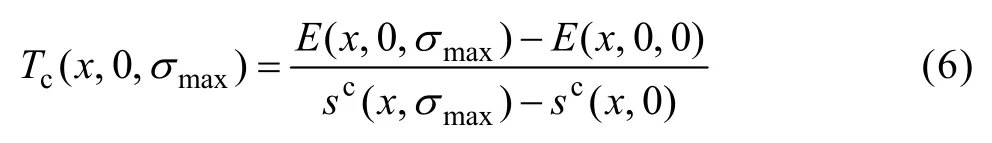
計算結果表明， 由第5E函數獲得的Tc溫度較其他E函數獲得的Tc溫度更接近實驗值(見圖3)。與此函數對應的特征原子勢能之間的關系為

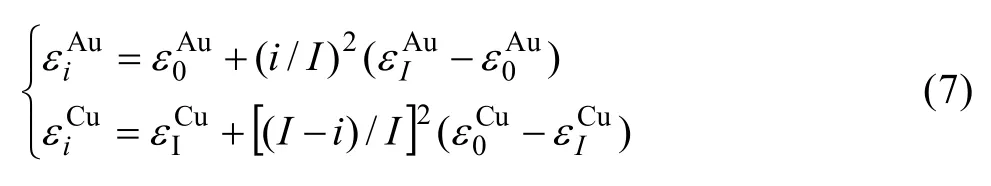
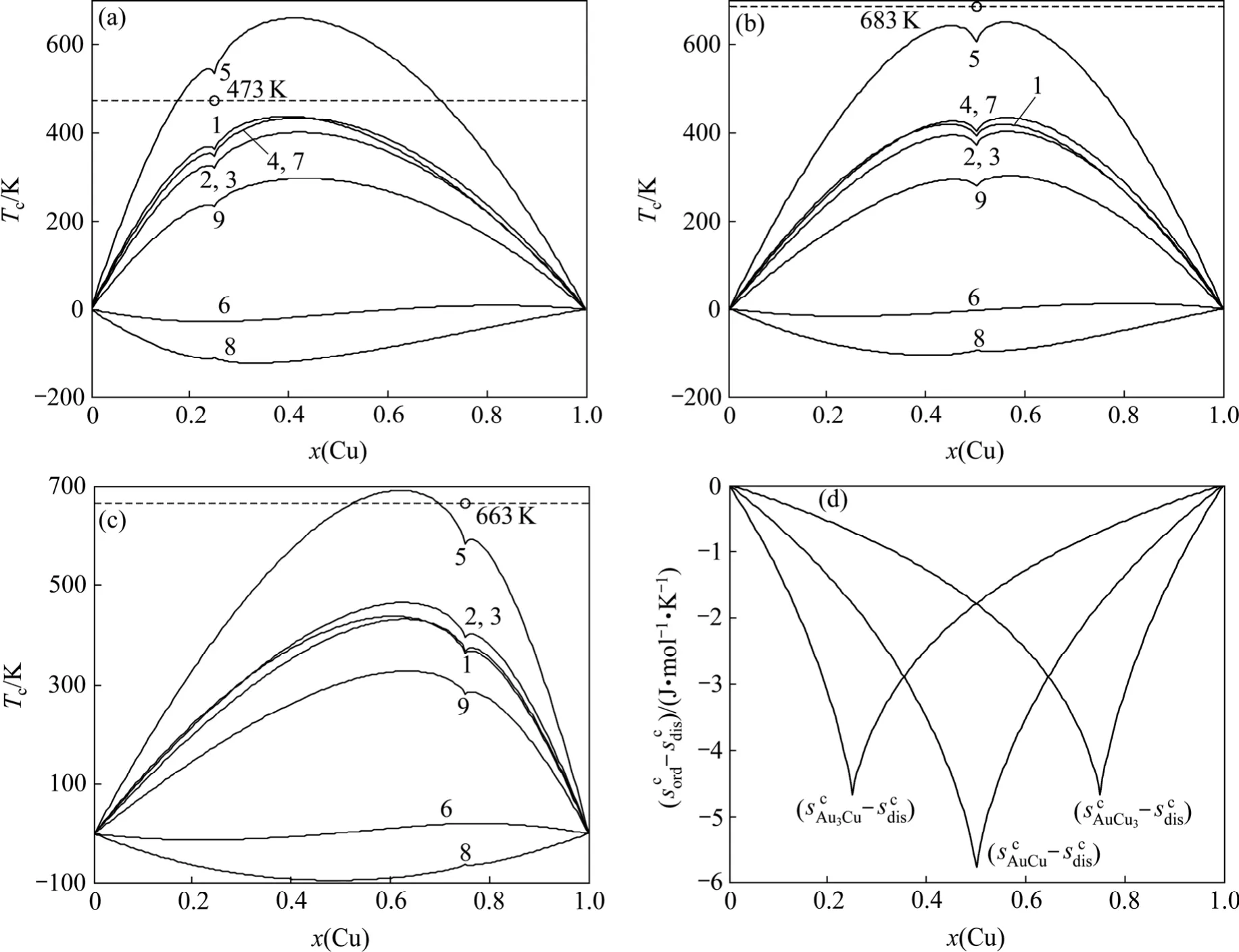
圖3 最大有序度Au3Cu、AuCu和Au3Cu型合金有序?無序轉變臨界溫度和熵差值Fig.3 Critical temperatures Tc ((a), (b), (c))and configurational entropies sc(x, σmax)differences (d)of Au3Cu- (a), AuCu- (b)and AuCu3- (c)type ordered alloys with maximum ordering degrees relative to disordered Au(1?x)Cux alloys (Dotted lines are experimental critical temperatures Tc of Au3Cu, AuCu and AuCu3 compounds)

Au-Cu系中特征原子的勢能列于表3[1]。它們屬于Au-Cu系的能級，適用于所有合金相：Au3Cu、AuCu和AuCu3化合物，成分可變的Au3Cu、AuCu和AuCu3型有序合金以及無序Au(1?x)Cux合金。

表3 Au-Cu系中特征原子 和的摩爾勢能Table 3 Potential energies of and characteristic atoms in Au-Cu system

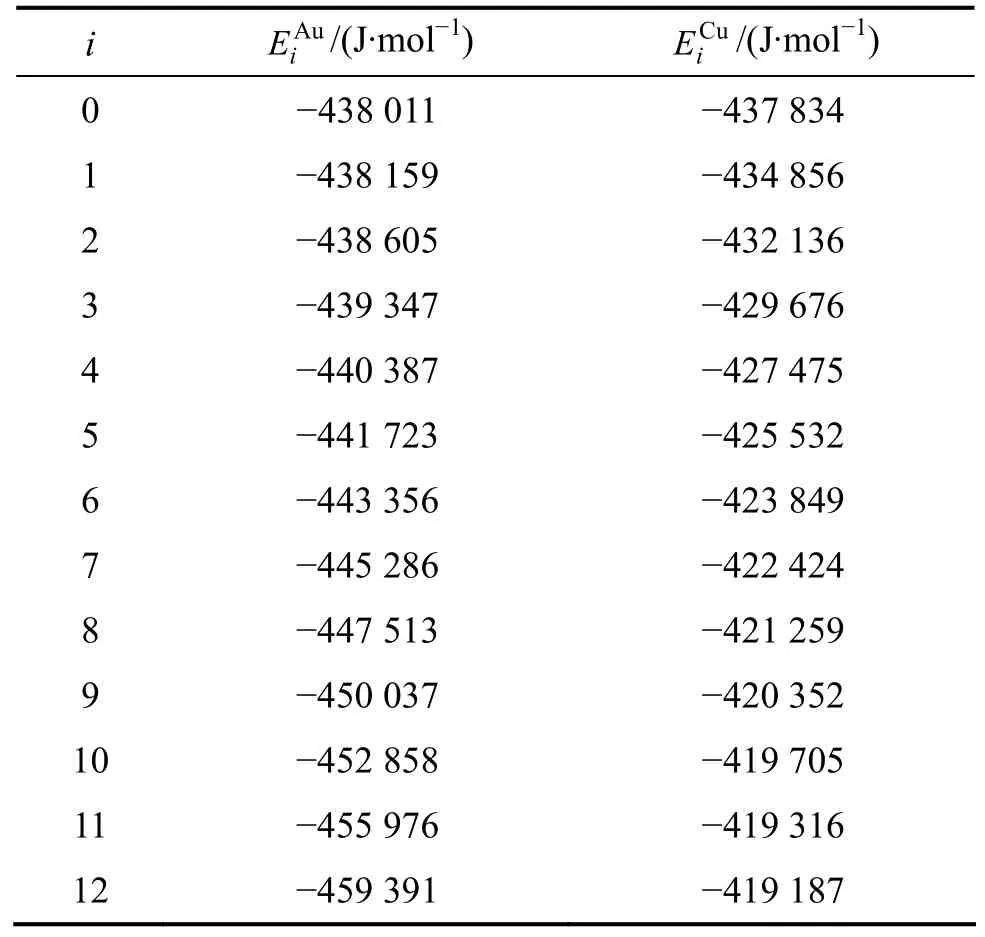
表3 Au-Cu系中特征原子 和的摩爾勢能Table 3 Potential energies of and characteristic atoms in Au-Cu system

i EAu i/(J·mol?1)ECui/(J·mol?1)

2 Au3Cu型有序合金相的 CAPE配分函數公式鏈

公式鏈表明，CAA模型本質上等同于 Bragg-Williams模型[15]和中心原子模型[16]的組合。CAPE配分函數考慮了特征原子的勢能能級和原子排列簡并因子之間的一致性。

1) CAPE配分函數

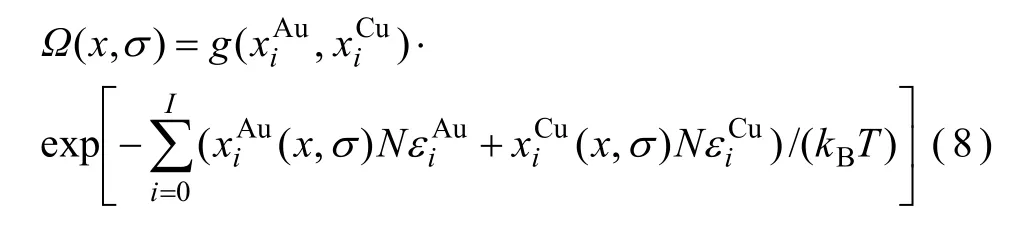
2) 簡并因數函數

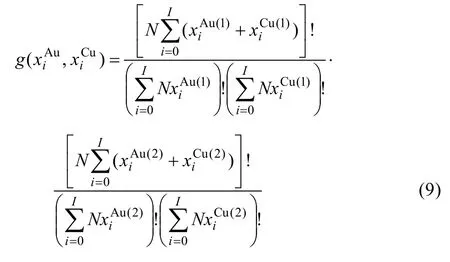
3) 組態熵函數

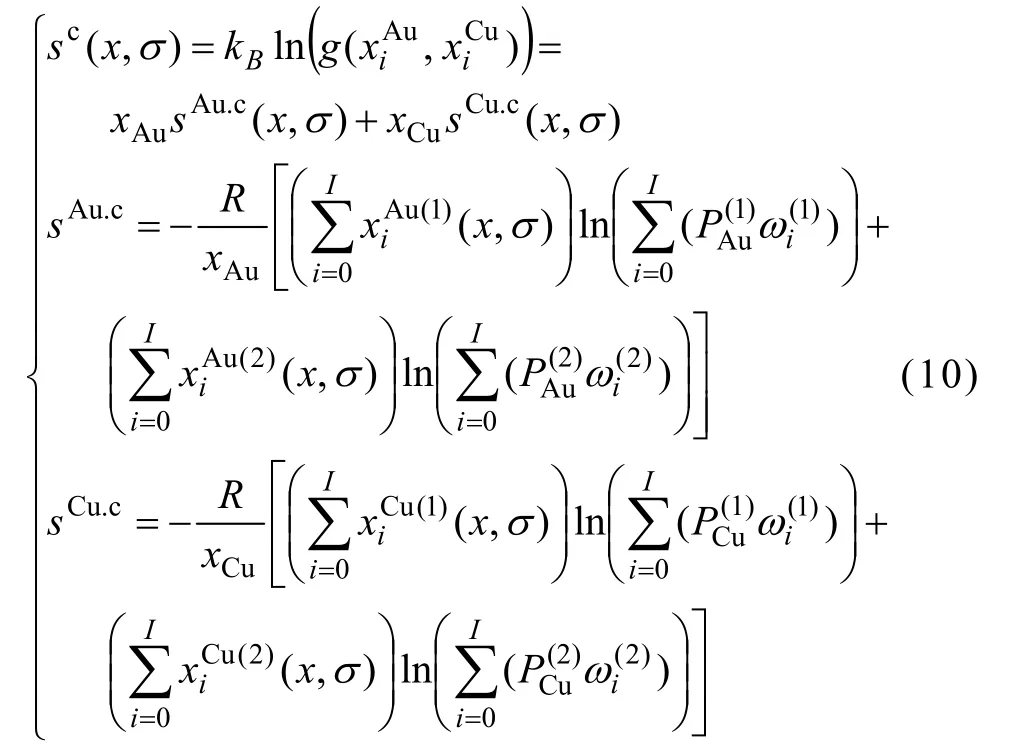
4) 特征原子濃度分布函數

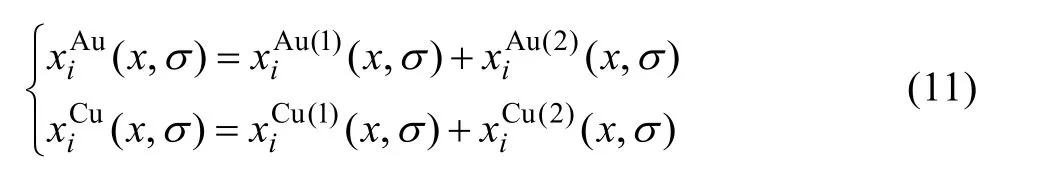
5) 占居第(1)和第(2)亞格點的特征原子濃度

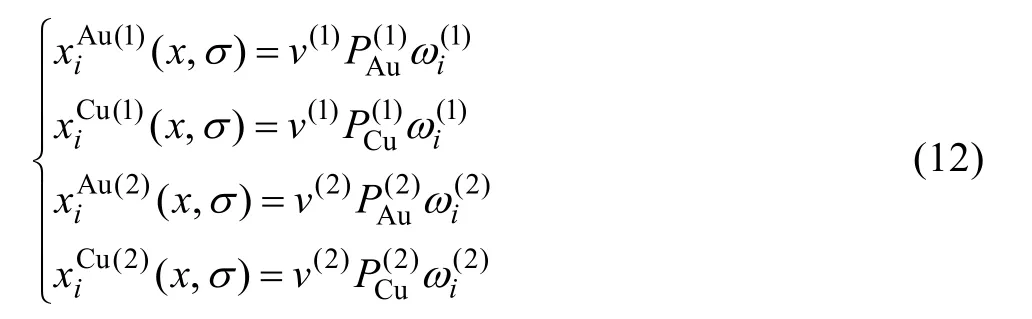
6) Au和Cu原子占居第(1)和第(2)亞格點概率

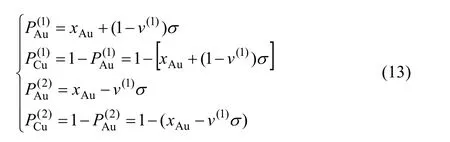
7) Au3Cu型有序合金的第(1)和第(2)亞格點分數

8) 有序度的定義

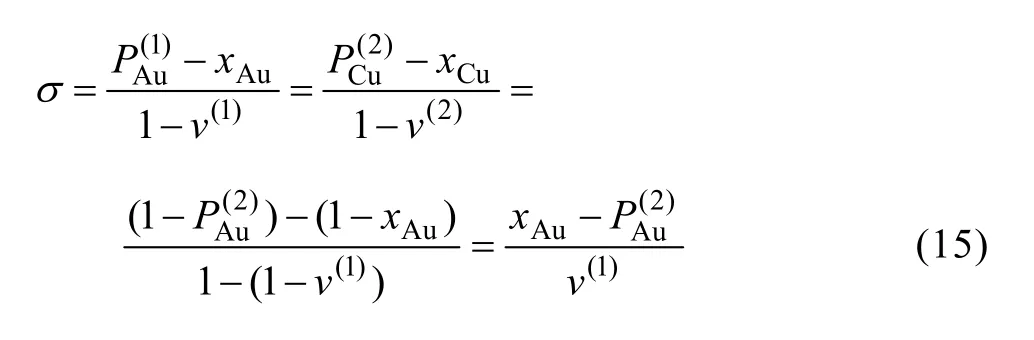
9) 圍繞第(1)亞格點的配位原子團 [( I -i )Au,iC u]的概率

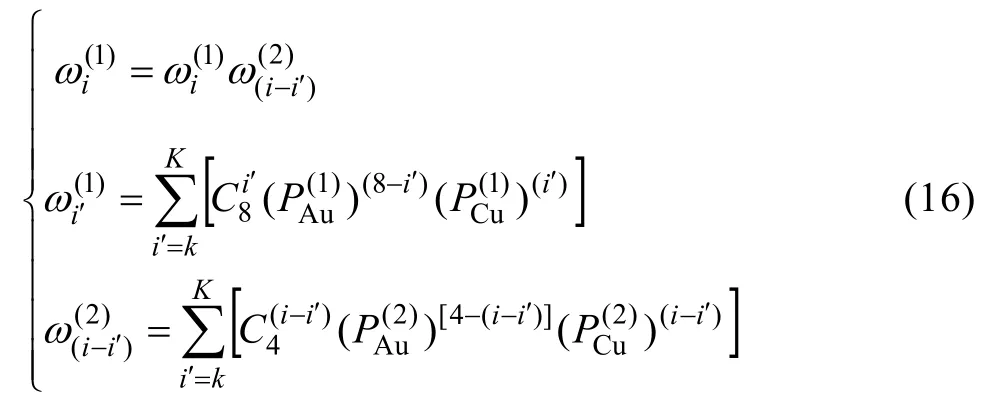
10) 圍繞第(2)亞格點的配位原子團[(I - i )Au,iCu]的概率

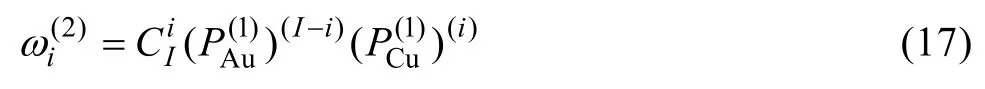
式(16)和(17)中，k和K按下列規則取值：

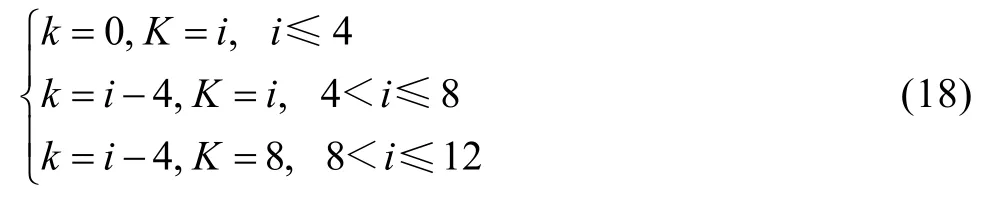
11) Au3Cu型有序合金最大有序度σmax與組元濃度的關系由式(15)得到：

12) 合金和組元的平均勢能(特征原子勢能相加定律)

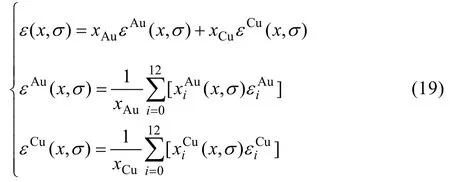
13) 0 K時合金和組元的平均生成焓

式(19)和(20)表明，Au組元和Cu組元的平均原子勢能(εAu，εCu)和生成焓( Δ hAu，ΔhCu)可直接獲得。而在傳統溶體理論中，組元的平均性質是由偏摩爾性質理論間接獲得，而這已證明是不正確的[1]。

應當指出的是，特征原子Gibbs能(CAGE)配分函數已經建立，但建立和說明它并不容易。

3 結果

應用 CAPE配分函數，計算 Au3Cu型有序合金Au(1?x)Cux的特征原子濃度(x,σ)和(x,σ)在勢能能級上的能級分布、特征原子勢能分布、合金及組元的勢能、生成焓和組態熵隨成分和有序度的變化，結果如圖4～8所示。

結果表明，CAPE配分函數考慮了特征原子的勢能能級和原子排列簡并因子之間的一致性，并且組元的平均勢能和平均生成焓不必采用偏摩爾性質理論可以直接得到。

4 討論

由特征原子勢能可建立由“特征原子對鍵能”描述的合金摩爾勢能公式：

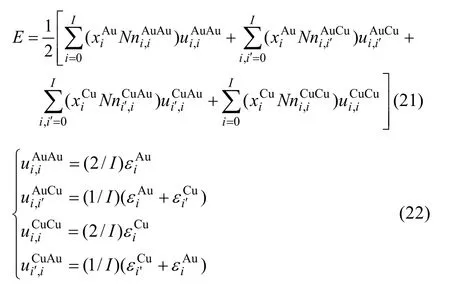
由L12-Au3Cu化合物中的摩爾勢能、特征原子勢能和特征原子對鍵能的關系可證明式(21)等同于式(19)：

表4 Au3Cu型有序合金中，圍繞第(1)亞格點的配位原子團[(I?i)Au, iCu]的概率的計算方法Table 4 Methods for calculating probability of coordinative cluster [(I?i)Au, iCu]surrounding (1)-sublattice point in Au3Cu-type ordered alloys

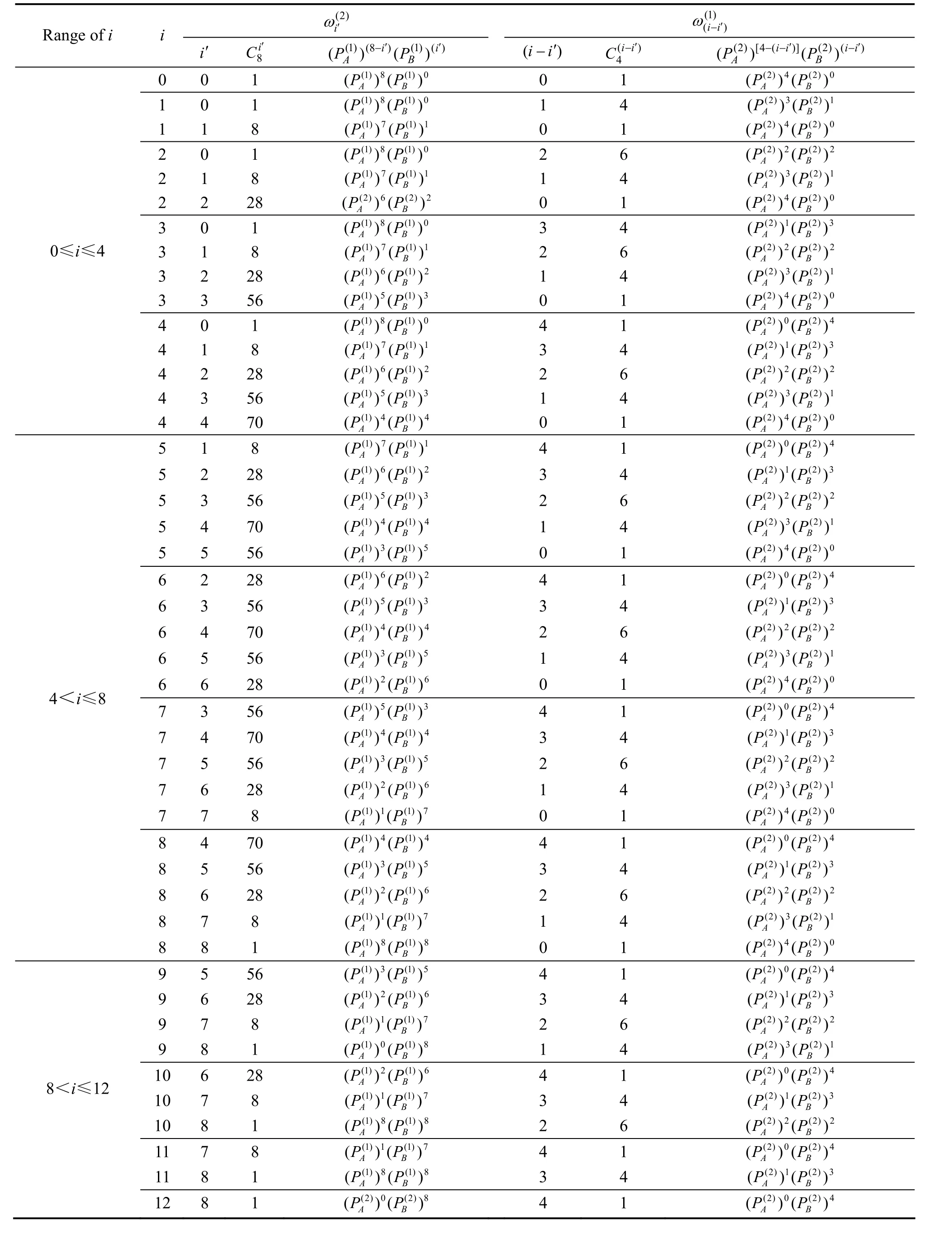
表4 Au3Cu型有序合金中，圍繞第(1)亞格點的配位原子團[(I?i)Au, iCu]的概率的計算方法Table 4 Methods for calculating probability of coordinative cluster [(I?i)Au, iCu]surrounding (1)-sublattice point in Au3Cu-type ordered alloys

0≤i≤4 4＜i≤8 8＜i≤12

表5 Au3Cu型有序合金中圍繞第(2)亞格點的配位原子團[(I?i)Au, iCu]概率的計算方法Table 5 Methods for calculating probability of coordinative cluster [(I?i)Au, iCu]surrounding (2)-sublattice point in Au3Cu-type ordered alloys

表5 Au3Cu型有序合金中圍繞第(2)亞格點的配位原子團[(I?i)Au, iCu]概率的計算方法Table 5 Methods for calculating probability of coordinative cluster [(I?i)Au, iCu]surrounding (2)-sublattice point in Au3Cu-type ordered alloys

i i C12 (1)()(P - i i A P(1)(I)i)(i A P)C12 (1)()(P -)(1)(I)i i B (B )

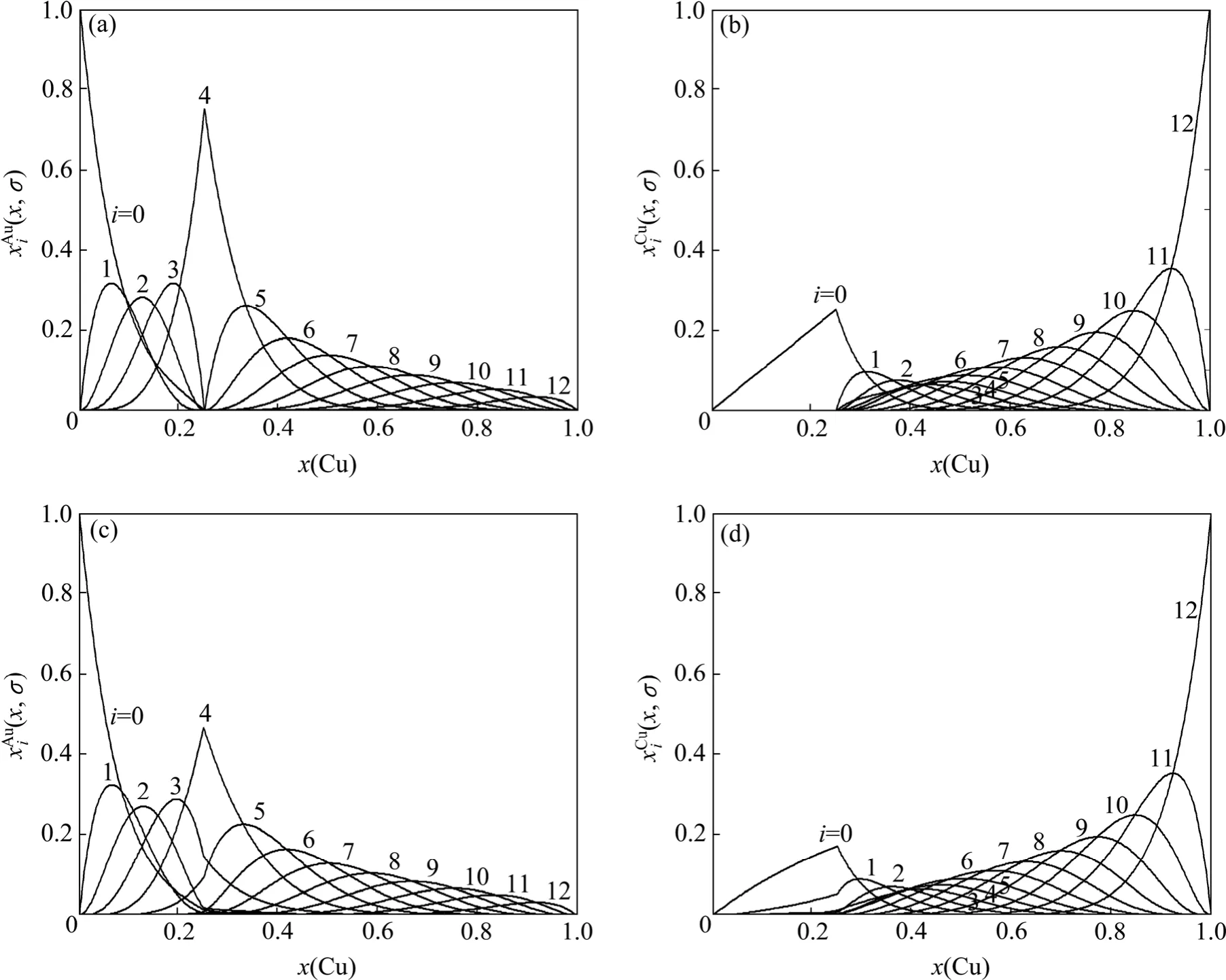
圖4 Au3Cu型有序合金Au(1?x)Cux的特征原子濃度(x,σ)和(x,σ)的分布Fig.4 Concentrational (x,σ)and (x,σ)distributions of characteristic atoms in Au3Cu-type ordered Au(1?x)Cux alloys corresponding to potential energy levels: (a)(x,σ), σ=σmax; (b)(x,σ), σ=σmax; (c)(x,σ), σ=0.9σmax; (d)(x,σ), σ=0.9σmax

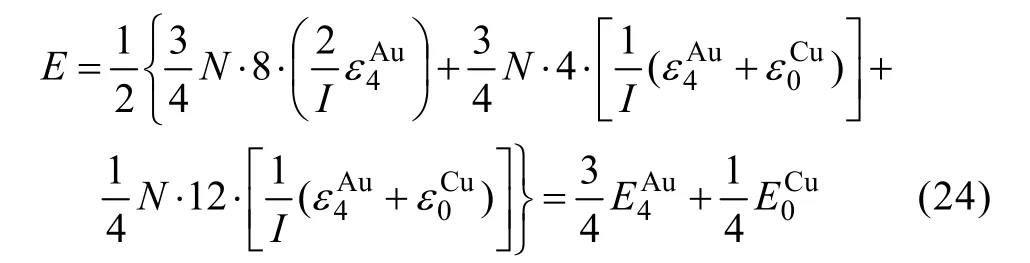
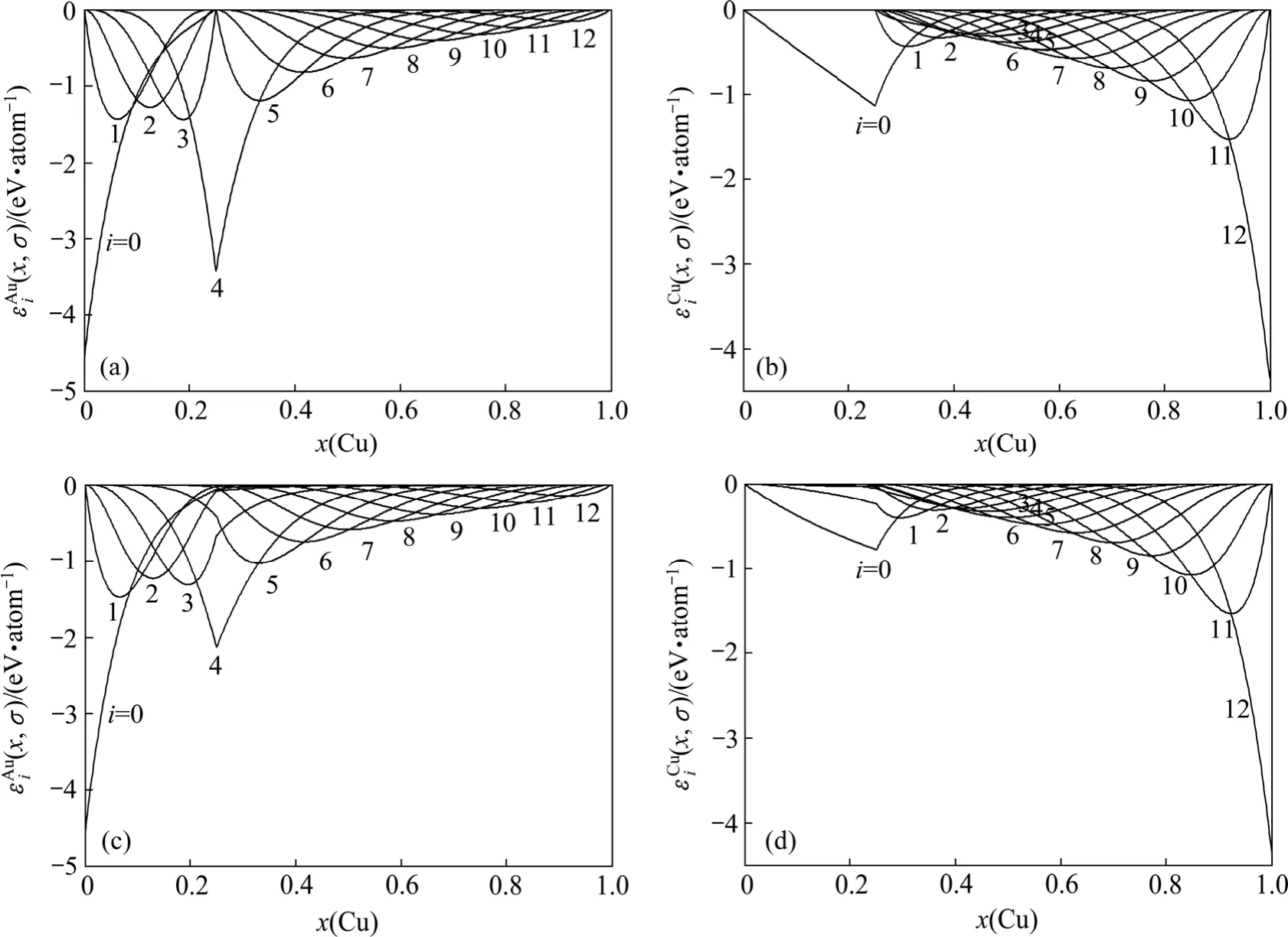
圖5 Au3Cu型有序合金Au(1?x)Cux中對應于勢能能級的勢能 (x,σ)= (x,σ)和 (x,σ)=(x,σ) 的分布Fig.5 Potential energy (x,σ)= (x,σ) and (x,σ)= (x,σ) distributions of characteristic atoms in Au3Cu-type ordered Au(1?x)Cux alloys corresponding to potential energy levels: (a) x,σ), σ=σmax; (b) (x,σ), σ=σmax;(c) ( x,σ), σ=0.9σmax; (d) (x,σ), σ=0.9σmax

圖6 Au3Cu型有序合金Au(1?x)Cux中合金和組元的摩爾勢能E(x,σ)、E A u(x,σ)和E C u(x,σ)與成分和有序度的關系Fig.6 Molar potential energies E(x,σ),E A u(x,σ)and E C u(x,σ)of Au3Cu-type ordered Au(1?x)Cux alloys and their components as functions of composition and ordering degree: (a)σ=σmax; (b)σ=0.9σmax; (c)σ=0.5σmax; (d)σ=0σmax

圖7 0 K時Au3Cu型有序合金Au(1?x)Cux中合金和組元的平均生成焓Δh(x,σ)、Δ h Au(x,σ)和Δ h Cu(x,σ)與成分和有序度的關系Fig.7 Molar formation enthalpies Δh(x,σ),Δ h Au(x,σ)and Δ h Cu(x,σ)of Au3Cu-type ordered Au(1?x)Cux alloys and their components as functions of composition and ordering degree at 0 K: (a)σ=σmax; (b)σ=0.9σmax; (c)σ=0σmax; (d)Δh(x,σ)at different σ values

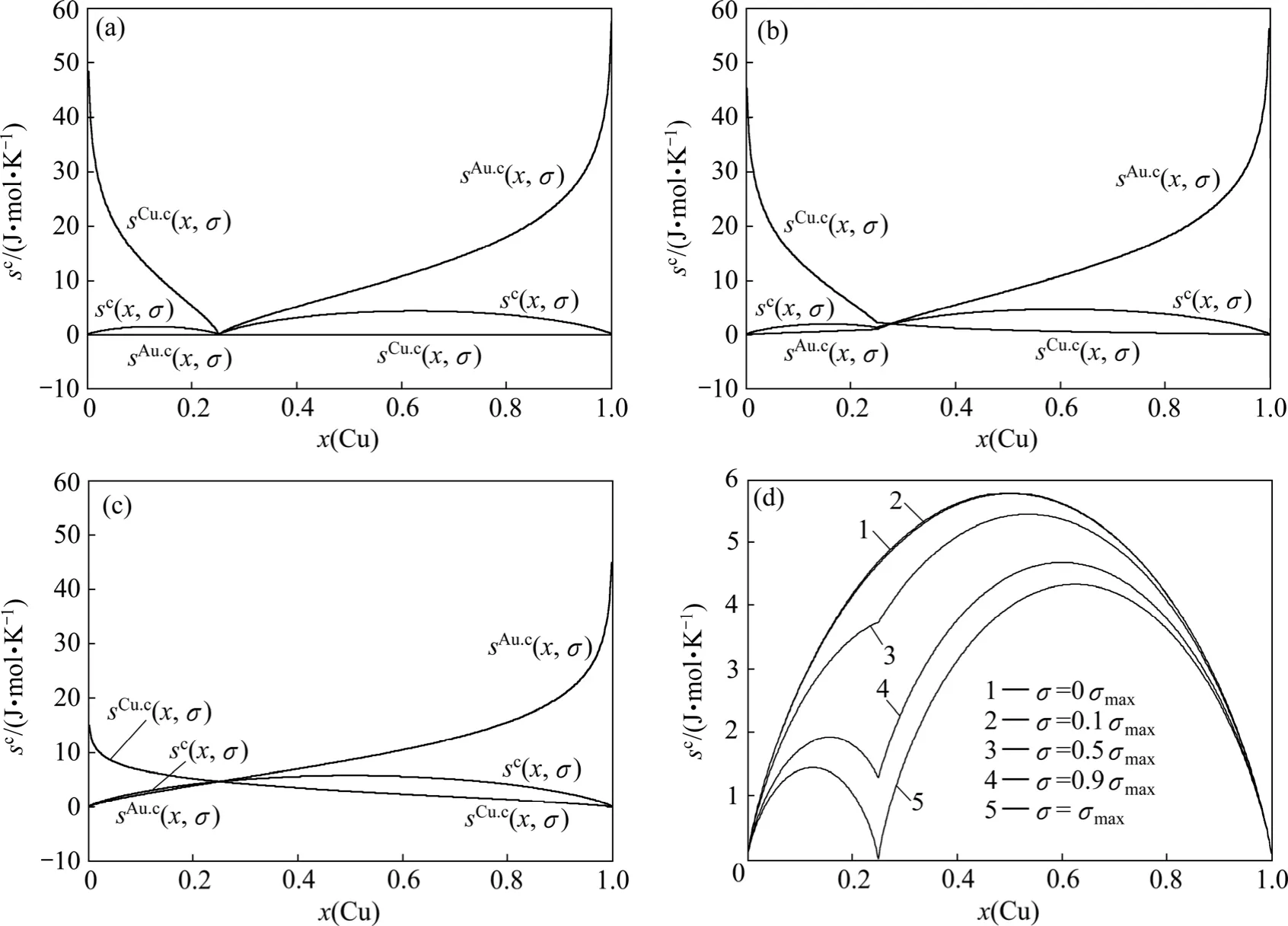
圖8 Au3Cu型有序合金Au(1?x)Cux中合金和組元的組態熵 s c(x,σ)、sA u.c(x,σ)和sC u.c(x,σ)與成分和有序度的關系Fig.8 Configurational entropies sc (x,σ), s A u.c(x,σ)and sC u.c(x,σ)of Au3Cu-type ordered Au(1?x)Cux alloys and their components as functions of composition and ordering degree: (a)σ=σmax; (b)σ=0.9σmax; (c)σ=0σmax; (d)s c (x,σ)at different σ values

比較式(21)和式(25)可知，CAA 模型和Bragg-Williams 模型的區別如下：CAA模型中，Au-Cu系的鍵能級別和是恒定的，其對應的原子數分別為和在 Bragg-Williams模型中，Au-Cu系的鍵能級別uAuAu、uAuCu、uCuAu和uCuCu不是恒定的，其對應的原子數分別為和

采用類似方法，可以確定特征原子團模型中合金相的摩爾勢能與特征原子團勢能的關系式。

根據以上分析，可得如下認識：

1) 在SSA框架中FCC基本格子Au-Cu系的基本結構單元是特征原子和序列，基本能級是和序列。它們可分別組成“組合結構單元序列”和“組合能級序列”。由13種和13種特征原子勢能可組合成=325種特征原子對鍵能和計算合金組態熵時應采用特征原子簡并因數，即式(9)。

因為合金相(即使為化合物)是組元原子按基本格子排列的溶體，所以，應該采用和特征原子作為最小結構單元描述各種不同相結構：Au3Cu、AuCu、AuCu3化合物，Au3Cu、AuCu、AuCu3型有序合金和無序合金。同理，應采用特征原子的勢能和作為描述這些合金系統的最精細能級。

2) 不難認識當今流行的 CALPHAD-CVM 和FP-CVM理論的不足之處：由于采用“組合結構單元”，組態熵值往往估算過大；由于采用組合能級使得這些理論均為總能框架，組元的平均能量性質只能間接地由偏摩爾性質理論獲得，然而，已經證明這是不正確的[1]。SSA則是能量可分離的框架。

5 結論

Au3Cu型有序合金特征原子勢能配分函數的創新體現在如下 3個方面：1) 以基本原子團和序列的中心特征原子和為結構單元序列，替代原子對和原子團，建立能闡明合金多樣性的特征原子排列模型。2) 以配位原子組態 [( I - i )Au, iC u]決定中心特征原子勢能的方式替代原子對能量相互作用方式和原子團之間能量相互作用方式，以特征原子勢能的基本能級替代“組元原子對”和“組元原子團”的能級，提出了以成分和有序度為變量的“特征原子勢能相加定律”，計算合金相及其組元的平均勢能。3)在保持特征原子濃度與特征原子勢能能級對應的條件下建立配分函數和計算組態熵。CAPE配分函數的重要意義在于它有可能推動材料科學由 CALPHAD-CVM 和FP-CVM 總能量框架向能量可分離的 EX-SSA和FP-SSA框架發展，使SSA框架具有堅實的哲學和物理學的基礎。

[1]XIE You-qing. Systematic science of alloy[M]. Changsha:Central South University Press, 2010: 29?48, 405?427,335?345.

[2]SUNDMAN B, FRIES S G, OATES A W. A thermodynamic assessment of the Au-Cu system[J]. CALPHAD, 1998, 22:335?354.

[3]KIKUCHI R. A theory of cooperative phenomena[J]. Phys Rev,1951, 81: 988?1003.

[4]SUNDMAN B, FRIES S G, OATES A W. A CALPHAD assessment of the Au-Cu system using the cluster variation method[J]. Z Metalkd, 1999, 90(4): 267?273.

[5]SATA M, de FONTAINE D, van SCHILFAARDE M.First-principles study of phase stability of Ti-Al intermetallic compounds[J]. J Mater Res, 1993, 8(10): 2554?2568.

[6]OATES W A. Configurational entropies of mixing in solid alloys[J]. Journal of Phase Equilibria and Diffusion, 2007, 28(1):79?89.

[7]XIE You-qing, PENG Kun, LIU Xin-bi. Influences of xTi/xAl on atomic states, lattice constants and potential energy planes of ordered FCC TiAl-type alloys[J]. Physica B, 2004, 344: 5?20.

[8]XIE You-qing, LIU Xin-bi, PENG Kun, PENG Hong-jian.Atomic states, potential energies, volumes, stability and brittleness of ordered FCC TiAl3-type alloys[J]. Physica B, 2004,353: 15?33.

[9]XIE You-qing, PENG Hong-jian, LIU Xin-bi, PENG Kun.Atomic states, potential energies, volumes, stability and brittleness of ordered FCC Ti3Al-type alloys[J]. Physica B, 2005,362: 1?17.

[10]XIE You-qing, TAO Hui-jing, PENG Hong-jian, LI Xiao-bo,LIU Xin-bi, PENG Kun. Atomic states, potential energies,volumes, stability and brittleness of ordered FCC TiAl2type alloys[J]. Physica B, 2005, 366: 17?37.

[11]XIE You-qing. Atomic energies and Gibbs energy functions of Ag-Cu alloys[J]. Science in China: E, 1998, 41: 146?156.

[12]OZOLIN? V, WOLVERTON C, ZUNGER A. Cu-Au, Ag-Au,Cu-Ag and Ni-Au intermetallics: First-principles study of temperature-composition phase diagrams and structure[J]. Phys Rev B, 1998, 57: 6427?6442.

[13]HULTGREN R, DESAI P D, HAWKINS D T, GLEISER M,KELLEY K K. Selected values of thermodynamic properties of binary metals and alloys[M]. OH: American Society for Metals,1963: 462.

[14]KITTEL C. Solid state physics[M]. 5th ed. New York: Wiley,1976: 74.

[15]BRAGG W H, WILLIAMS E J. The effect of thermal agitation on atomic arrangement in alloys[J]. Proc Roy Soc A, 1934, 145:699?730.

[16]LUPIS CHP. Chemical thermodynamics of materials[M].Amsterdam: North-Holland, 1983: 452?469.