橢圓曲線上的信息論安全的可驗證秘密共享方案

田有亮，馬建峰，彭長根，陳曦

（1. 西安電子科技大學 通信工程學院，陜西 西安 710071；2. 西安電子科技大學 計算機學院，陜西 西安 710071；3. 貴州大學 理學院，貴州 貴陽 550025）

1 引言

在密碼體制中，可以將關鍵控制和權利分發給團體中的成員進行管理，以分散加/解密、簽名和驗證權利。1979年，Shamir[1]和 Blakley[2]分別基于Lagrange插值多項式和射影幾何理論提出門限秘密共享方案，就是為了解決此類問題。Stadler[3]提出在線秘密共享機制，引入公告牌（NB）發布一些輔助信息。文獻[4,5]研究了將模運算用于秘密共享，提出了基于中國剩余定理的秘密共享方案。文獻[6]討論了多項式的運算與數的運算以及Lagrange 插值多項式與中國剩余定理的相似性。近年來，研究人員主要針對多秘密共享、防欺騙等方面展開研究[7,8]。

為了解決在Shamir的秘密共享方案中存在的2個問題。1)莊家（秘密的持有者）的誠實性：若莊家將錯誤的子秘密分發給部分或全部成員，各成員如何驗證莊家發送來的子秘密是正確的？2)成員的誠實性：在恢復秘密階段，若某些惡意的成員提供的是假的子秘密，其他成員如何鑒別？對這2個問題的研究，就形成了可驗證的秘密共享方案（簡記作VSS）。首次提出這種思想的是文獻[9]，而Feldman[10]的工作則使這種秘密共享方案受到了眾多密碼研究者的重視。隨后，Pedersen[11,12]給出了更為簡潔、實用的方案。但是，無論在Shamir的一般秘密共享方案中，還是在VSS方案中，都需要假設莊家和各成員之間有秘密信道（private channel）,以便分發子秘鑰。在文獻[13～15]中，也對該問題進行了研究，但都存在諸多缺點：文獻[13]中需對每個共享秘密作預計算，而且子秘密的認證需要各方在線合作，從而計算量和通信量都很大；Harn提出的方案[14]，其安全性是基于離散對數的難解性，為了防止參與者之間的欺詐，需要執行一個交互式驗證協議，計算量非常大；Hwang和Chang[15]提出了一個多重秘密共享方案，但該方案存在分發者計算量大，效率不高等缺點。

眾所周知，橢圓曲線密碼系統在密鑰長度、安全性等方面都比基于大整數分解和離散對數的密碼系統更具有優勢。而橢圓曲線上的雙線性對是構造加密、簽名等諸多密碼算法的重要工具，如：代數曲線上的Weil Pairing和Tate Paring。在2000年，Weil Pairing被用來構造Key Agreement[16]，這是Key Agreement協議的一個突破；在2001年的密碼學會上，Boneh和Franklin利用橢圓曲線上的雙線性對設計了基于身份的加密方案[17]；同年的亞密會上，Boneh、Lynn和Shacham提出基于雙線性對的短簽名方案[18]；此后，許多基于BLS短簽名方案被提出。雙線性對技術成為構造諸多密碼算法的重要工具，同時也促進這些方面的蓬勃發展。然而，基于雙線性對技術對秘密共享進行研究相對較少。最近，Shi等[19]基于橢圓曲線上的離散對數問題提出了(t, n)門限可驗證多秘密共享方案；Wang等[20]用雙線性對提出了動態可驗證多秘密共享方案；田有亮等基于雙線性對技術研究了秘密共享方案的可驗證性[21～23]和可公開驗證性[24]問題，有效地將雙線性對技術引入到秘密共享方案中以解決秘密共享的可驗證性及可公開驗證性；他們提出用雙線性對的雙線性性質解決秘密共享的可驗證性問題[25,26]。李慧賢等[23]利用雙線性對構建可證明安全的秘密共享方案的新方法，基于公鑰密碼體制的語義安全的標準定義，提出了適合秘密共享方案的語義安全定義，并提出了一個新的基于雙線性對的門限秘密共享方案，對其正確性、安全性和性能進行分析討論和證明。

可見，以雙線性對技術為工具深入研究秘密共享方案，無論是在理論上，還是在實際應用中都具有重要的價值和意義。本文針對上述提到的問題，在田有亮等工作[25]的基礎上，從不同的角度，提出一種橢圓曲線上的信息論安全的可驗證秘密共享方案及無可信中心的可驗證密碼共享方案。本文也間接提出了一種基于雙線性對的完備隱藏、完美綁定的知識承諾方案。秘密共享方案在防止莊家及參與者之間的欺詐行為時，與文獻[25]一樣，不需要執行復雜的交互式協議，僅通過雙線性對的雙線性性質就可以實現，避免了以往很多方案為了實現可驗證行而需要交互大量信及秘密分發者計算量大的缺點。性能分析表明該方案具有較小的計算量和通信量，提高了秘密共享方案的效率。

2 準備知識

2.1 雙線性對

定義1 設G1、G2是2個相同素數階為q的加法群和乘法群，q是一大素數。設P為G1的任一生成元。aP記為a個P相加。假設在群G1和G2上的離散對數問題（DLP）都是困難的。映射e: G1×G1→G2滿足如下性質①～③被稱為密碼學上的雙線性映射。

①雙線性：對?P,Q∈ G1和a, b∈, e( aP, bQ)=e( P, Q)ab；或者對?P, Q, R∈G1,e( P+Q, R)=e( P, R) e( Q, R)和e( P, Q+R)=e( P, Q) e( P, R)。

②非退化性：如果P是G1的生成元，則e( P, P)是G2的生成元，也即e( P, P)≠1。

③可計算性：對?P, Q∈G1，都存在有效的算法來計算e( P, Q)。

2.2 Diffie-Hellman問題

Diffie-Hellman問題定義如下：考慮加法群G =＜g＞，G的2個元素g1:= ag和g2:=bg，并且知道生成元g，但不知道a和b。問題是：計算g3=(ab)g。有如下相關定義。

定義2 設G是有限循環群，g是G的生成元。

1) 離散對數問題(DLP)：給定(g, ag)，對任意的a∈，求a。

2) 計算性Diffie-Hellman問題(CDHP)：給定(g, ag, bg)，對任意的a, b∈，計算(ab) g。

3) 判定性Diffie-Hellman問題(DDHP)：給定(g, ag, bg)，對任意的a, b∈，判斷 (ab) g=cg是否成立。

在群G上，DDHP是易解的，即DDHP在多項式時間內能夠被解決；而CDHP是難解的，即沒有任何可能的算法可以解決CDHP。此時稱群G為GDH群。

2.3 雙線性Diffie-Hellman問題

有許多密碼體制（如基于身份的加密體制、短簽名方案等）的安全性是基于雙線性對的相關Diffie-Hellman問題的。雙線性Diffie-Hellman問題首先是在文獻[17]中被提出的。考慮G1是素數階的加法群，其階為q，并且P是它的生成元。設q階乘法群G2且它們之間存在雙線性映射e：G1×G1→G2，能被有效計算。

定義3 雙線性Diffie-Hellman問題(BDHP) 描述如下 ：在(G1, G2, e)中，給定(P, aP, bP, cP)，對任意的a, b, c∈R,計算e( P, P)abc∈G2。

算法Α在解決BDH問題被稱為有優勢ε，如果

Pr[Α(P, aP, bP, cP)=e( P, P)abc]≥ε

其中，a, b, c∈R,P∈G1。

BDH假設可描述為：在求解BDH問題上，沒有概率多項式時間算法有不可忽略的優勢。

3 可驗證密碼共享方案

3.1 方案描述

假設有莊家D需在n個參與者U={U1,…,Un}間共享秘密S，僅當t個或t個以上的參與者聯合起來才能恢復共享秘密，少于t個參與者的任何組合都無法得到關于秘密的任何信息。具體方案由4個子協議組成：系統初始化、秘密分發協議、子密鑰的驗證協議和秘密重構協議。

系統初始化。G1是素數階的加法群（這里為橢圓曲線群），其階為q；P和Q是它的2個生成元，且任何人都不知道n∈，滿足Q=nP；設q階乘法群G2且它們之間存在雙線性映射e：G1×G1→G2，能被有效計算；G1和G2上的離散對數（G1上是橢圓曲線離散對數）都是難解的；秘密S∈G1。

秘密分發協議。分發協議分為以下5步。

1) 莊家D公布秘密S的承諾：C0=C(S,r)= e(S+rQ,P), ?r∈R。

2) 莊家D選取G1[x]上的次數最多為t-1的秘密多項式F( x)=S+F1x+…+Ft-1xt-1滿足S=F(0)(這里Ft-1xt-1表示在橢圓曲線群G1上xt-1個Ft-1相加)，并計算Si=F(i)，i=1,…,n 。

3) 莊家D隨機選取g1,…,gt-1∈R，并廣播Ci=C(Fi,gi)=e(Fi+giQ P），i=1,…,t-1。

5) 莊家D秘密發送(Si,ri)給Ui,i=1,…,n。

子密鑰的驗證協議。Ui接受到(Si,ri)后，可通過式（1）驗證子密鑰的正確性：

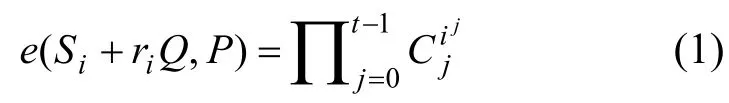
秘密重構協議 當至少t個成員iU(iB∈且||Bt≥)提供他們各自的子密鑰),(iirS后，即可利用Lagrange插值函數來計算出秘密S和r：

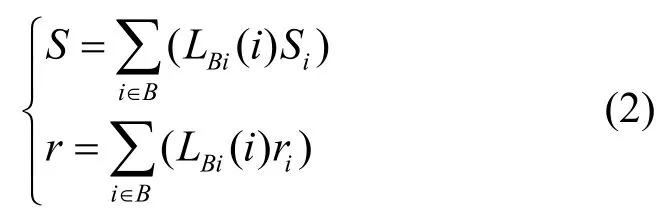
其中，LBi(i)為插值系數，。

隨后可利用公開信息0C驗證),(iirS的正確性：C0=e(S+rQ,P)。

3.2 安全性與正確性分析

首先證明式(1)的正確性。

證明 因為Si=F( i)和ri=g(i)，所以有:

e(Si+riQ,P)=e(Si,P)e(riQ,P)

=e( F( i), P) e( g( i) Q, P)

=e( S, P) e( iF1, P)…e( it-1Ft-1,P)

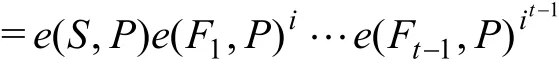
同理，e( g( i) Q, P)=e(rQ,P)e(g1Q,P)i…e(gt-1Q,P)it-1

所以e( F( i), P) e( g( i) Q, P)證畢。

下面分析方案的安全性。

引理1 上述VSS方案中，對在G1上的多項式F( x)的系數F0, F1,…,Ft-1承諾C0, C1,…,Ct-1是安全的?BDH假設成立。

證明 ?用反證法。假設上述方案中的承諾算法是安全的，但BDH假設不成立。則由BDH假設不成立知，存在算法A：對于G1中給定的P, aP, bP, cP，算法A能以成功率ε計算出e( P, P)abc。現在證明，利用算法A可以破解上述承諾算法。要破解上述承諾算法，只需從Ci中計算出Fi即可。為此，隨機選取元素α,β,γ,α',β',γ'∈R，然后分別將(P,αP,βP,γP)和(P,α'P,β'P,γ'P)作為輸入提供給算法A。由于該輸入是隨機的，故算法A將以成功率ε分別輸出e(P,P)αβγ和e(P,P)α'β'γ'。又由于Ci=e(P,P)αβγe(P,P)α'β'γ'，則e((αβγ)P, P)=Ci/e(P,P)α'β'γ', 從而可求出。這與承諾算法是安全的相矛盾。因此，若上述方案中的承諾算法是安全的，則BDH假設必然成立。

?同樣用反證法。假設BDH假設成立，但上述方案中的承諾算法是不安全的。那么由承諾算法不安全知，存在算法B：將任何G1中的隨機元素Q1,Q2,Q3∈RG1作為算法B的輸入時，算法B能以成功率ε計算出Fi，滿足：Ci= e(Fi+riP,P)=e(Q1+Q2,Q3)。若設Fi=αP，riP=βP，α,β∈和Q1=α1P ，Q2=α2P，Q3=α3P，α1,α2,α3,∈R，則算法B能以成功率ε計算出Fi滿足：e((α1+α2)P,α3P)=e((α+β)P,P)。由此我們可得=e(P,P)。令a=(α1+α2)，b=α3，c=(α+β)-1，這就表明算法B對于G1中給定的(P, aP, bP, cP)，算法B能以成功率ε計算出(,)abce P P。這與假設矛盾！因此，若假設BDH假設成立，則上述方案中的承諾算法就是安全的。

綜上所述，方案中的承諾算法就是安全的?BDH假設成立。證畢。

引理2 上述VSS方案中，若BDH假設成立，則任何1t-個成員聯合都不能恢復秘密S。

證明 用反證法。假設t-1個成員聯合能夠恢復秘密S。不失一般性，假設這t-1個成員就記為：U1,…,Ut-1。現要證明，對任給的αP,βP,γP，攻擊者I利用這t-1個成員作為預言機（Oracle），就能計算出e( P, P)αβγ。不妨設α, β, γ是隨機元素，否則，就用3個隨機元素α', β', γ'∈R對αP,βP,γP進行隨機化。

現在來為攻擊者I設置一個模擬的VSS系統，使得當U1,…,Ut-1作為預言機時，就可以計算出e( P, P)αβγ。模擬系統的設置分為以下5步。

1) 攻擊者I置C0=e(αP +βP,γP)；這樣，C0的設置就隱含地確定了F(0)=αγP和g(0)Q=βγP。

3) I計算前t-1個e(Si+riQ,P)i=1,…,t-1的值。

4) 由于F(0)和g(0)是隱含在C0中的，故I沒法計算(F(t),g(t)),…,(F(n),g(n))的值；但是，I可利用Lagrange插值公式計算出余下的e(Si+riQ,P)(i=t,…,n)。

5) 計算Ci( i=1,2,…,t -1)。由于F(x)=S和，故可得如下方程組：

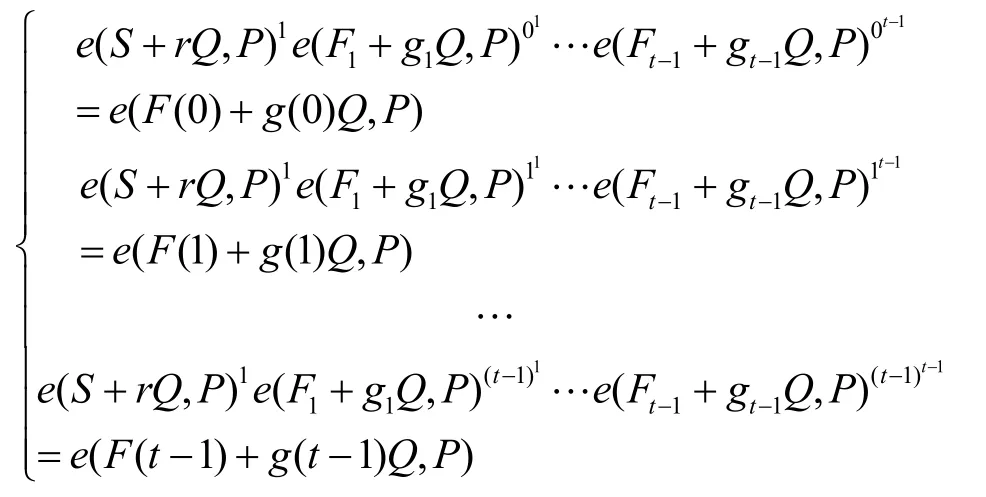
在上述方程組中，敵手I只知道(F(1),g(1))，…，(F(t -1),g(t-1))的值，不知道(F(0),g(0))的值。因此，I不能解出S,F1,…,Ft-1和r,g1,…,gt-1的值。然而I知道C0，故I利用C0和方程組就可以計算出Cj(j=1,…,t-1)。

這樣，一個模擬的VSS系統就設置完成了。當攻擊者I將這一系統的相關信息提供給這t-1個成員U1,…,Ut-1時，他們的個人觀察（private view）是相互一致的。那么根據假設，這t-1個成員U1,…,Ut-1就可以計算出秘密F(0)滿足：e(αP+βP ,γP)=e(F(0)+g(0)Q,P)?e(P,P)αβγ=e(β-1(F(0)+g(0)Q),P)e(P,γP)-1。由于系統中的雙線性對是能被有效計算的，這就表明這t-1個成員能求解BDH問題。這與BDH假設成立相矛盾，從而命題成立。證畢。

利用引理1和定理2，有如下定理。

定理3 VSS方案是信息論安全的，也就是說，任何t個成員聯合都可以重構莊家分發的秘密S，而任何1t-個成員構成的子集都不能得到該秘密的任何信息。

證明 設任意的B?{U1,…,Un}，且|B|=t-1。B的觀察viewB(C0,…,Ct-1;(Si,Ti)i∈B)，則命題需證明：Pr[UigetsS|viewB]= Pr[UigetsS]＜ε，?Ui∈B。

根據引理1知道，對任意的S∈RG1，若是隨機、均勻選取的，則C(S,r)=e(S+rQ,P)均勻分布于G2中。若BDH假設成立，則莊家D不能用2種方式打開C(S,r)。由于C(S,r)具有良好的隨機性，故有Pr[Dhassecret S|viewB]=Pr[Dhassec ret S]。

由引理2有，若BDH假設成立，對于?Ui∈B，Pr[UigetsS]=Pr[UigetsS|viewB]=；另一方面，對于?Ui∈B，Pr[UigetsS]=。因此，Pr[UigetsS]=Pr[UigetsS|viewB]=。從而命題得證。

3.3 信息率

本節主要考慮方案的信息率(information rate)。在本文方案中，其共享秘密S∈G1，所以|S|=2|q|；方案中其共享子密鑰為(Si,ri)，而Si∈G1，ri∈。因此，|(Si,ri)|=|Si|+|ri|= 3|q|。根據信息率的定義知，其信息率為

文獻[11]和文獻[24]中方案的信息率都是1/2；文獻[23]中方案的信息率是1/5；而本文方案的信息率為2/3。可見，在相同安全等級下（都是信息論安全的），本文方案有較高的信息率。

3.4 性能分析

本節通過與現有方案進行比較來簡單分析本文方案的性能。為了便于與現有方案的比較，主要選取基于離散對數問題及其相應困難性假設的秘密共享方案進行類比。例如，基于離散對數問題(DLP)的方案選取文獻[14]為代表，基于橢圓曲線離散對數問題(ECDLP)及相應假設的選取文獻[22]和文獻[24]為代表。這里，主要考慮方案的計算、通信等方面性能比較。眾所周知，基于DLP的方案，其最為耗時的運算是冪模運算，用pT表示；基于ECDLP的方案，其最為耗時的運算是點乘運算，用Ta表示；基于雙線性對技術的方案，最耗時的運算包括：群1G(設其為有限域上的橢圓曲線群)上的點乘運算(aT)、群2G(設其為有限域)上的冪模運算(pT)及之間的對運算(記為eT)；其他計算開銷忽略不計。下面，通過表1將本文方案與這些方案做一簡單比較。

通過表1做如下兩方面的分析比較。

1) 計算量方面。在系統建立過程中，本文方案的莊家D不需要為各位參與者計算相應的密鑰，此時的計算開銷可以不加考慮。而文獻[14]、文獻[22]和文獻[24]中均需為各參與者計算相應的密鑰，這是本方案在計算上占優的一個方面。在秘密分發階段(因文獻[14]是一個多秘密共享方案，為了與本方案具有可比性，表1中僅列出該方案共享子密鑰Si(=F(i))及公開信息Ci(i=0,…,t-1)，所共享單個秘密計算量及通信量等)，莊家D需要為每一位參與者計需要的群G1上的點乘運算次數及雙線性對計算次數分別為t(n+1)和 2t次；從表1可以看出本文方案在這方面沒有明顯優勢。在子秘密驗證階段，共需要n次對運算、n次點乘運算和群G2上tn次指數運算，本文方案僅與文獻[24]中的方案有明顯優勢。在秘密重構階段，計算代價可以表示成群G1上t次點乘運算。可見，本文方案在這方面有明顯的計算優勢。盡管如此，但可以發現，本文方案的主要運算開銷與參與者數目成線性關系；而且在秘密分發階段有些計算可以作預處理，這樣可以大大提高秘密分發的效率。

表1 本文方案與現有方案的性能比較

2) 通信量方面。本文方案在莊家分發子密鑰時，需要點對點通信。分發公開信息可以采取廣播方式。在秘密重構時，亦需要點對點的單播通信。因此總通信次數為1nt++。本文方案的通信次數遠遠低于文獻[14]中方案的通信次數，主要在子秘密驗證通信方面具有非常大的優勢；與文獻[22]和文獻[24]中方案通信次數相同(但在子秘密驗證的計算開銷方面本文方案有較大的優勢)。從表1可以看出，在總體通信開銷上本文方案具有非常明顯的優勢。

綜合以上兩方面的分析表明，本文方案具有相對較小的計算開銷及通信開銷，具有更好的實際應用價值。同時，方案具有線性性質，很容易推廣到無可信中心(無莊家)的情況，第4節的無可信中心的秘密共享方案也具有這些優點。

4 無可信中心的秘密共享方案

無論在一般的秘密共享，還是在可驗證的秘密共享方案中，都需要有一個莊家D（或者叫可信第三方：TTP）來分發秘密。一般假設莊家D是誠實的并且各參與者都信任D。但是，在現實中很難找到這樣的一個可信中心；這就成為了秘密共享方案發展中的一個瓶頸。本節將上節的方案推廣到無可信第三方的情況。

為了方便，記上節的秘密共享方案為：BDHVSS((S,r);Ci,(Si,ri);(F(x),g(x)))，其中，S：共享秘密，r：隨機數；Ci：公共信息；(Si,ri)：Ui的分享子密鑰；(F(x),g(x))：莊家D選取的兩隨機函數。顯然，本文方案是線性的，因此有如下結論。

定理2 給定2個執行實例：Instance 1：BDHVSS((S,r);Ci,(Si,ri);(F(x),g(x))) 和Instance 2：BDHVSS((S',r');Ci',(S'i,r'i);(F'(x),g'(x)))?一個執行實例Instance 3： BD H VSS((S+S',r+r');CiCi',(Si+Si',ri+ri');(F'( x)+F'( x), g( x)+g'( x)))。

證明 因秘密共享方案具有線性性質，所以該定理顯然成立。

下面設計無可信中心的可驗證秘密共享方案。假設秘密S∈G1要在n個成員間共享。所有假設同上節，則其無可信中心的秘密共享方案如下。

方案包括3步：秘密的分發、計算子密鑰和秘密的重構。

秘密的分發。成員Ui(i=1,…,n)執行協議：

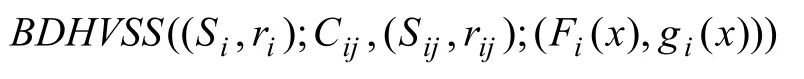
計算子密鑰。所有的成員成功分發了他們的子密鑰后，參與者(i=1,…,n)Ui通過下式計算他的共享份額(Si,ri)：

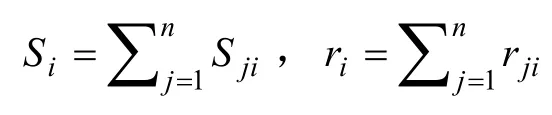
秘密的重構。當至少t個成員iU(iB∈且||Bt≥)提供他們各自的子密鑰),(iirS后，即可利用Lagrange插值函數來計算出秘密(S, r)。

記上述無可信中心的可驗證秘密共享方案為：NDVSS((Si,ri);Cij,(Sij,rij);(Fi(x),gi(x)))。很容易得到如下定理。

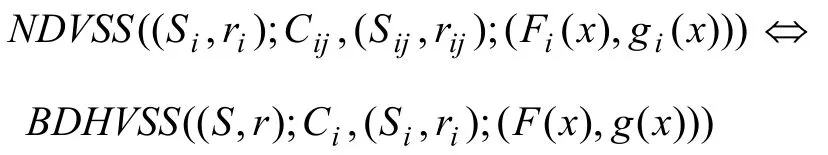
證明 該結論是定理2的自然推廣，證明略。

5 結束語

橢圓曲線上的雙線性對是構造諸多密碼算法的重要工具。本文基于該技術研究可驗證秘密共享方案，構造了通信效率高、安全性更好的可驗證及無可信中心的可驗證秘密共享方案。利用雙線性對的雙線性性質，提高了方案中子秘密驗證的有效性。再者，通過對方案的有效性和安全行分析顯示，所提方案均滿足可驗證秘密共享方案的特性，同時在BDH困難性假設下本文方案是信息論安全的。與已有方案的對比顯示，所提方案具有較小的計算開銷和通信開銷，并提高了信息率。

[1] SHAMIR A. How to share a secret[J]. Communications of the ACM,1979, 22(11): 612-613.

[2] BLAKLEY G. Safeguarding cryptographic keys[A]. Proceedings of the National Computer Conference[C]. AFIPS, 1979.313-317.

[3] STADLER M. Publicly verifiable secret sharing[A]. Cryptology-EUROCRYPT’96[C]. Berlin, 1996. 190-199.

[4] ASMUTH C, BLOOM J. A modular approach to key safeguarding[J].IEEE Trans on Information Theory, 1983, 29(2): 208-210.

[5] HWANG R J, CHANG C C. An improved threshold scheme based on modular arithmetic[J]. Journal of Information Science and Engineering,1999, 15(5): 691-699.

[6] AH O, ULLMAN J. The Design and Analysis of Computer Algorithms[R]. Reading, MA: Addison-Wesley, 1974.

[7] CHAN C W, CHANG C C. A scheme for threshold multi-secret sharing[J]. Applied Mathematics and Computation, 2005, 166(1): 1-14.

[8] CHANG T Y, HWANG M S, et al. An improvement on the LinWu (t,n) threshold verifiable multi-secret sharing scheme[J]. Applied Mathematics and Computation, 2005, 163(1): 169-178.

[9] CHOR B, DOLDWASSER S, MICALI S, et al. Verifiable secret sharing and achieving simultaneity in the presence of faults[A]. Proc 26th IEEE Symposium on Foundations of Computer Sciences(FOCS'85)[C]. Los Angeles, 1985. 383-395.

[10] FELDMAN P. A practical scheme for non-interactive verifiable secret sharing[A]. Proc 28th IEEE Symposium on Foundations of Computer Science (FOCS’87)[C]. 1987. 427-437.

[11] PEDERSON T P. Non-interactive and information-theoretic secure verifiable secret sharing[A]. Cryptology-CRYPTO’91[C]. Berlin:Springer-Verlag, 1992. 129-140.

[12] PEDERSON T P. Distributed Provers and Verifiable Secret Sharing Based on the Discrete Logarithm Problem[D]. Aarhus, Denmark:Aarhus University, Computer Science Department, 1992.

[13] MTOPA H. How to share a secret with cheaters[J]. Journal of Cryptology, 1988, 1(2): 133-138.

[14] HARM L. Efficient sharing (broadcasting) of multiple secrets[J]. IEEE Proc Comput Digital Tech, 1995, 142(3): 237-240.

[15] HWANG R J, CHANG C C. An on-line secret sharing scheme for multi-secrets[J]. Computer Communications, 1998, 21(13): 1170-1176.

[16] JOU X. A one round protocol for tripartite Diffie-Hellman[A]. Proceedings of ANTS 4[C]. 2000. 385-394.

[17] BONEH D, FRANKLIN M. Identity based encryption from the Weil pairing[A]. Extended Abstract in Crypto 2001[C]. 2001. 586-615.

[18] BONEH D, LYNN B, SHACHAM H. Short signatures from the Weil pairing[A]. Journal of Cryptology, 2004, 17:297-319.

[19] SHI R H, ZHONG H, HUANG L S. A (t, n)-threshold verified multi-secret sharing scheme based on ECDLP[A]. The Eighth ACIS International Conference on Software Engineering, Artificial Intelligence,Networking, and Parallel/Distributed Computting[C]. 2007. 9-13.

[20] WANG S J, TSAI Y R, SHEN J J. Dynamic threshold multi-secret sharing scheme using elliptic curve and bilinear paring[A]. 2008 Second International Conference on Future Generation Communication and Networking[C]. 2008. 405-410.

[21] TIAN Y L, PENG C G, et al. A practical publicly verifiable secret sharing scheme based on bilinear pairing[A]. Proceedings of the 2nd International of Conference on Anticounterfeiting, Security, and Identification (2008ASID)[C]. Guiyang, China, 2008. 71-75.

[22] 田有亮, 彭長根. 基于雙線性對的可驗證秘密共享方案[J]. 計算機應用, 2007, 27 (B12): 125-127.TIAN Y L, PENG C G. Verifiable secret sharing scheme based on bilinear pairing[J]. Computer Applications, 2007, 27(B12): 125-127.

[23] 李慧賢, 龐遼軍. 基于雙線性變換的可證明安全的秘密共享方案[J]. 通信學報, 2008, 29(10): 45-49.LI H X, PANG L J. Provably secure secret sharing scheme based on bilinear maps[J]. Journal on Communication, 2008, 29(10): 45-50.

[24] 田有亮, 彭長根. 基于雙線性對的可驗證秘密共享方案及其應用[J]. 計算機工程, 2009, 35 (10): 158-161.TIAN Y L, PENG C G. Verifiable secret sharing and its applications based on bilinear pairings[J]. Computer Engineering, 2009, 35(10):158-161.

[25] 田有亮, 馬建峰, 彭長根. 基于雙線性 Diffie-Hellman問題的可驗證秘密共享方案[A]. 2009年中國密碼學會議[C]. 廣州，中國，2009.170-179.TIAN Y L, MA J F, PENG C G. Verifiable secret sharing based on bilinear Diffie-Hellman problem[A]. Chinacrypto2009[C]. Guanzhou,China, 2009. 170-179.

[26] 田有亮. 基于雙線性對的分布式密碼系統與應用研究[D]. 貴陽：貴州大學碩士學位論文, 2009.TIAN Y L. The Study on Distributed Cryptosystem and Its Application Based on Bilinear Paring[D]. Guiyang: Master Thesis Guizhou University, 2009.