基于卡爾曼濾波的潛器運動狀態觀測器*
劉常波 劉 培 丁風雷
(海軍潛艇學院作戰指揮系1) 青島 266071)(海軍潛艇學院研究生隊2) 青島 266071)
1 引言
潛器的自動控制,多是采用基于反饋構成的閉環結構,這種結構對內部參數變動和外部環境影響都有良好的抑制作用。反饋的基本類型包括“狀態反饋”和“輸出反饋”,狀態反饋可以完整的反饋系統的結構信息,在性能上也遠優于輸出反饋。
但某些狀態變量在系統中不可測量,需要引入附加的狀態觀測器。潛器的運動方程是非線性微分方程,經典的卡爾曼濾波只能處理線性方程,通過對潛器運動方程線性化,建立相應的狀態觀測器,給出狀態變量的估計值。
在弱機動時潛器的運動可以分解成垂直面運動和水平面運動,本文以航速穩定的垂直面運動方程為例,設計其狀態觀測器,并根據某一給出水動力系數的深潛器,建立模型,給出仿真結果。
2 潛器垂直面運動方程及其線性化
考慮潛器的垂直面運動,假定航速近似穩定,對潛器六自由度方程簡化,建立運動方程如式(1)所示,取潛器的重心為坐標原點。

方程組(1)是簡化的垂直面潛器運動方程,將其看作一個系統的狀態方程,狀態變量為垂向速度w,縱傾角速度q,縱傾角θ,深度ζ。縱傾角θ和深度ζ可由儀器直接測量,為系統輸出。在一定航速u下,系統的輸入是首升降舵角δb和尾升降舵角δs。狀態w和q,不能直接測量,是需要估計的量。理論上對輸出的縱傾角θ和深度ζ求導可以得出w和q,但潛器上的深度計和縱傾儀精度有限,對其求導不能得到較為精確的W和q,可以用卡爾曼濾波建立相應的狀態觀測器估計w和q。經典的卡爾曼濾波只能處理線性系統,狀態方程(1)是一組非線性方程,對其線性化得到垂直面線性運動方程(2)。

整理成標準形式如式(3)所示,由卡爾曼濾波,即可給出潛器垂直面運動的狀態觀測器

3 潛器垂直面運動的狀態觀測器
采用連續系統的卡爾曼濾波,潛器垂直面運動非線性系統的數學模型如下:
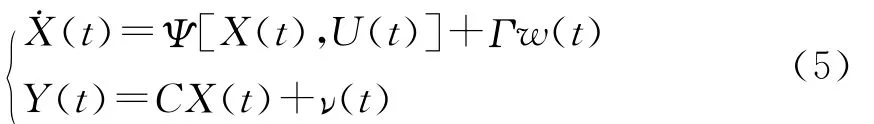
w(t)為隨機性的干擾輸入,ν(t)為量測噪聲,其噪聲統計特性如下:

其中,R1(t),R2(t)分別是w(t)及ν(t)的譜密度,δ(t)是置于t=0處的一階脈沖函數。

圖1 潛器垂直面運動狀態觀測器框圖
潛器在水中的運動,可分成水平面運動和垂直面運動,以垂直面運動方程為例,建立狀態觀測器,框圖如圖1所示。
狀態估計方程如式(7)所示,估計誤差協方差陣P(t)的傳播方程如式(8)所示,卡爾曼增益陣K(t)如式(9)所示,初始條件如式(10)所示:

式中A,B,C,如式(4)所示,過程噪聲w(t)的統計特性R1(t)由潛器航行時的內外環境所定,量測噪聲ν(t)的統計特性R2(t)由縱傾角θ深度ζ的精度確定。由框圖可知,狀態觀測器通過簡化的線性模型預測狀態值,然后通過量測信息更新預測值,得到估計的狀態值。以上采用的線性模型比較簡單,由此得出的預測值不夠精確,主要靠量測信息來修正。量測信息(深度和縱傾)的精度高,其中包含的信息就多,由此得到的狀態估計值就準確。
以Fossen在“Guidance and Control of Ocean Vehicles”書中給出的水下潛體為例,建立模型仿真。建立非線性運動方程,描述潛體的真實運動,用上述狀態觀測器,給出系統狀態的估計值。
4 仿真結果
編程仿真,分析比較非線性模型計算出的系統狀態量和觀測器給出的狀態估計量,狀態量縱傾角θ和深度ζ可由儀器量測,只比較垂向速度w和縱傾角速度q的估計值與真實值。
運行程序,給出量測輸出θ(縱傾角)和ζ(深度)的精度分別為1、0.1、0.001、0.001(度或米)的仿真結果,潛器速度4節,艏升降舵0°,艉升降舵打上浮舵5°。
潛器速度4節,艏升降舵0度,艉升降舵打上浮舵5度時,不同量測精度下,狀態觀測器的估計誤差,如表1所示。

表1 不同精度下狀態觀測器的估計誤差

圖2 縱傾角速度q的真實值與估計值比較

圖3 垂向速度w的真實值與估計值比較
5 結語
根據實際的仿真結果可以看出,觀測器的估計誤差與量測輸出的精度有關,量測輸出的精度越高,觀測器的估計誤差就越小。因此采用高精度的深度計和縱傾儀,可以降低觀測器的估計誤差。卡爾曼濾波主要靠模型預測和新的信息修正來估計狀態,優化預測模型,采用擴展卡爾曼濾波,能得到更好的效果。由仿真結果還可以看出,當潛器的運動狀態變化緩慢時,觀測器能更好地跟蹤潛器的真實運動狀態。
[1]施生達.潛艇操縱性[M].北京:國防工業出版社,1995
[2]胡坤,吳超.潛艇垂直面運動仿真及分析[J].青島大學學報,2003,16(4)
[3]張晶.潛艇運動建模及簡化技術研究[D].哈爾濱工程大學碩士研究生學位論文,2009
[4]賈欣樂,楊鹽生.船舶運動數學模型[M].大連:大連海事出版社,1999
[5]Thor I.Fossen.Guidance and Control of Ocean Vehicles[M].University of Trondheim,1994

