三角域上三次DP曲面的擴展

吳曉勤1，唐運梅1，韓旭里2

?

三角域上三次DP曲面的擴展

吳曉勤，唐運梅，韓旭里

（1. 湖南科技大學數學與計算科學學院，湖南湘潭411201; 2. 中南大學數學科學與計算技術學院，湖南長沙410083）

給出了三角域上帶雙參數的四次DP混合函數，它是三角域上三次DP 基函數的擴展。分析了該組混合函數的性質并定義了三角域上帶雙形狀參數的四次DP參數曲面。該組混合函數及其參數曲面分別具有與三次DP基函數及三次DP參數曲面類似的性質。當兩參數為0時，可分別退化到三次DP基函數及三次DP參數曲面。研究表明，通過改變兩個形狀參數的取值，既可整體又可局部調整曲面的形狀。

計算機應用；曲面設計；DP曲面；三角域；形狀參數

隨著幾何造型工業的發展，往往要求調整曲面的形狀或改變曲面的位置。一種方法是引進權因子，此為有理形式的曲線曲面，但有理曲線曲面也有一定的缺陷：如何選取權因子以及權因子對曲面的形狀影響還不是十分清楚，而且存在求導和求積運算較麻煩等問題。另一種方法是引進形狀參數，典型的有：Barskey的－樣條曲線，通過放松連續性條件，在基函數中引進了兩個參數以調整曲線的形狀；Zhang 提出三次C-曲線，Chen 等推廣到一般的C-Bézier 曲線，呂勇剛等在均勻節點上構造C-B 樣條曲線，Wang 等在一般的非均勻節點C-B 樣條曲線構造方法，其后統一為-B樣條；Han在三角多項式空間給出了帶形狀參數的二次和三次三角多項式樣條曲線等。

帶有形狀參數的曲線，運用張量積方法很自然推廣到矩形域的曲面上；但在三角形域上如何構造帶有形狀參數的曲面片，研究的文獻不多。2006年曹娟等給出了帶一個形狀參數的三角域上三次Bernstein-Bézier參數曲面的擴展；作者給出的帶一個形狀參數的+1次Bézier三角曲面片；鄔弘毅等給出的帶多個形狀參數的Bézier曲線與曲面的構造方法，由于該方法中的參數較多，從而大大增加了構造曲線與曲面的復雜性。其后，于立萍給出了三角域上帶兩個形狀參數的Bézier 曲面的擴展方法，曹莞薔等在三角多項式空間給出了三角域上擬Bézier基，得到了相應三角域上曲面片。上述曲面片利用形狀參數的不同取值實現對曲面形狀調控。

本文針對三角域上三次DP曲面進行擴展研究。通過提高多項式的次數，得到了三角域上10個帶有兩個參數的混合函數，分析了該組混合函數的性質，基于該組混合函數定義了帶有形狀參數的四次DP曲面，該曲面具有與三次DP曲面類似的性質：如角點插值、對稱性、凸包性、幾何不變和仿射不變性等。當兩參數為0時，曲面可退化為三次DP參數曲面。研究表明，通過改變兩個形狀參數的取值，既可整體又可局部調整曲面的形狀。

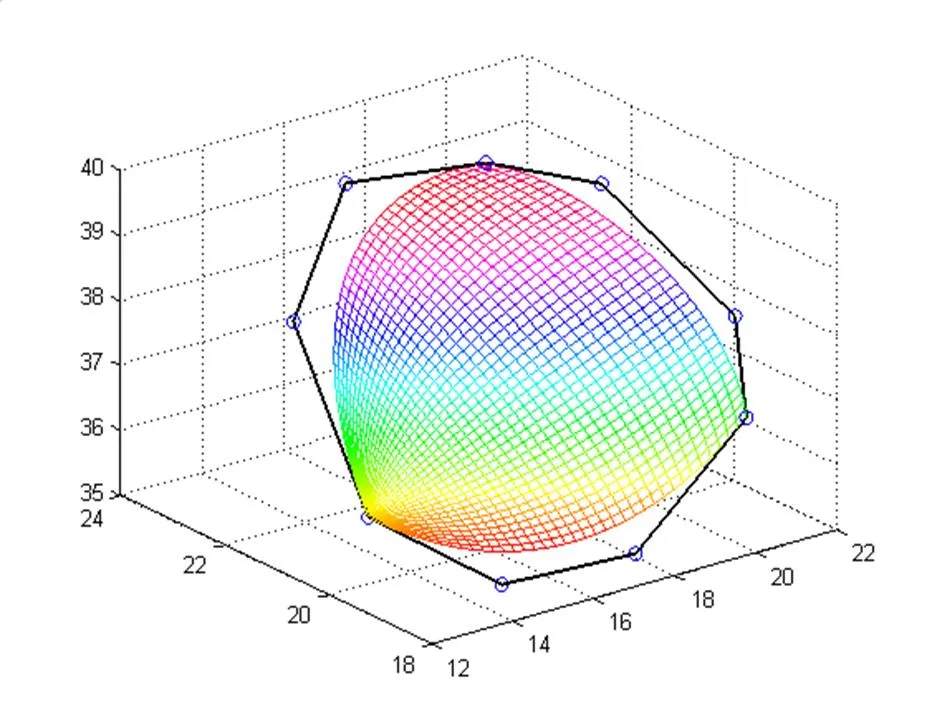
圖1 三角域上三次曲面片（左為三次Bézier曲面片，右為三次DP曲面片）

1 三角域上三次DP曲面片

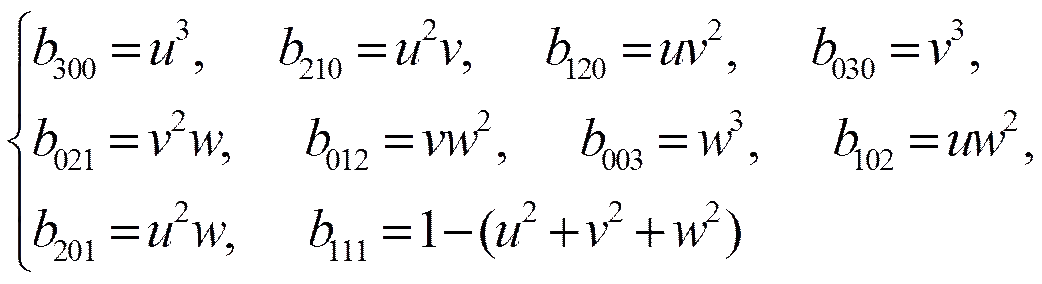
為三角域上三次DP基。

由定義1，給出DP曲面定義。

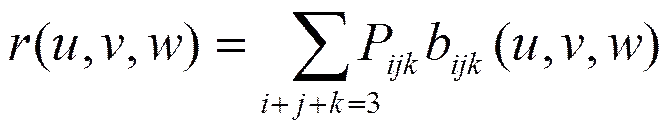
稱式（2）所定義的曲面為三角域上三次DP曲面片。

圖1為在相同控制網格點的三角域上三次Bézier曲面片和三次DP曲面片。

三次DP曲面片具有與三次Bézier曲面片同樣的性質，如：① 角點插值；② 對稱性；③ 凸包性；④ 幾何不變性和仿射不變性等。

2 三次DP曲面片的擴展

2.1 混合函數及其性質

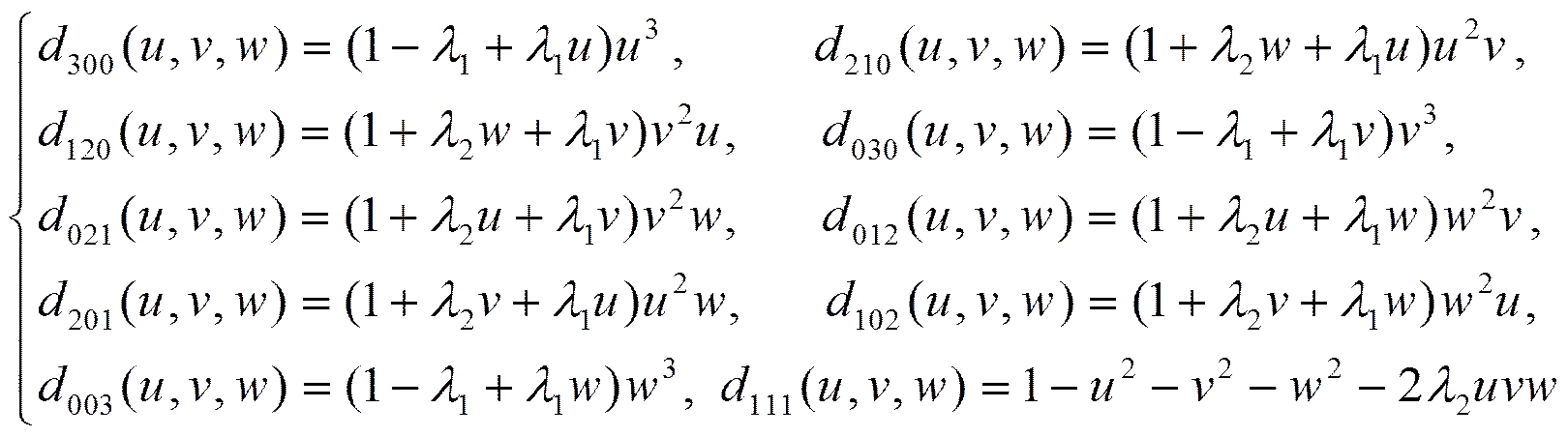
式(3)混合函數具有如下性質：

由式(2)不難驗證。

（3）對稱性，即

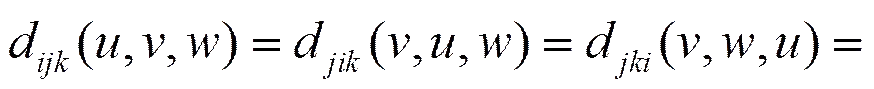
（4）角點性質，即

（5）線性無關性

因此，所給的混合函數是三次三角域上DP基函數的拓展。

2.2 曲面的結構及其性質

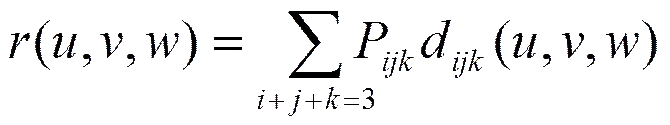
稱式（4）所定義的曲面為帶有形狀參數的四次DP三角曲面片。

由混合函數的性質，可知式（4）定義的曲面片具有與三次DP曲面片相同的性質：① 角點插值性質； ② 對稱性；③ 凸包性；④ 幾何不變性和仿射不變性；此外，還有性質⑤ 局部可調性，即改變參數、的值可局部調控曲面的形狀；⑥ 退化性，即當時，式(4)定義的曲面就是式(2)定義的曲面。

3 參數的幾何意義

（5）

（6）

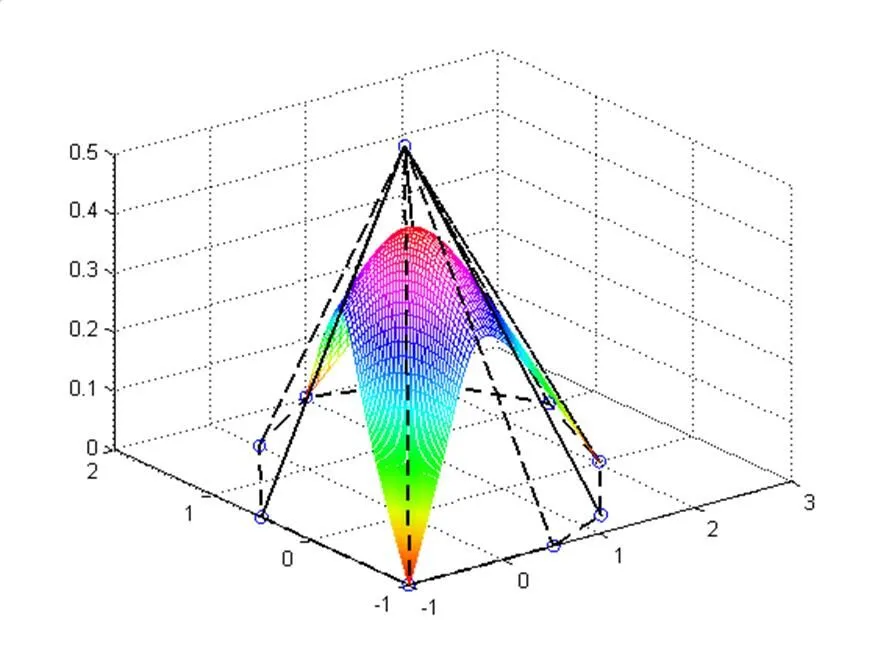
=1,=-1=1,=0

=0,=1=-1,=1

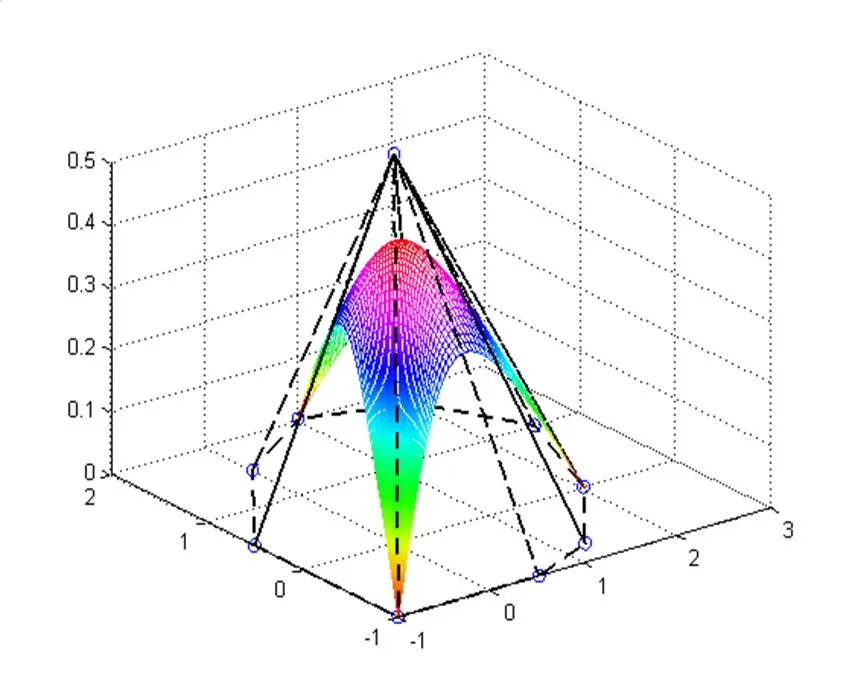
l1=0,l2=-1??????????????l1=-1,l2=0

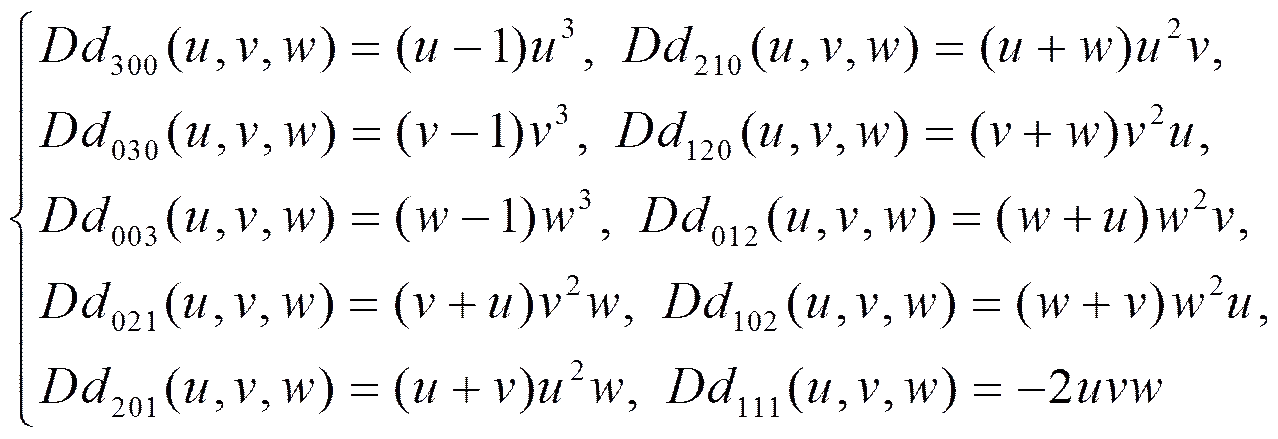
4　結 論

本文提出的三角域上帶兩個形狀參數的四次DP曲面是三次DP曲面的拓展，曲面具有三次DP曲面的特性：如角點插值、對稱性、凸包性、幾何不變和仿射不變性等；兩個參數具有明顯的幾何意義，既能整體又可局部的調控曲面的形狀。因此，可作為一種有效的幾何造型方法應用于曲面設計領域。實例表明引入兩個形狀參數是件有意義的工作。

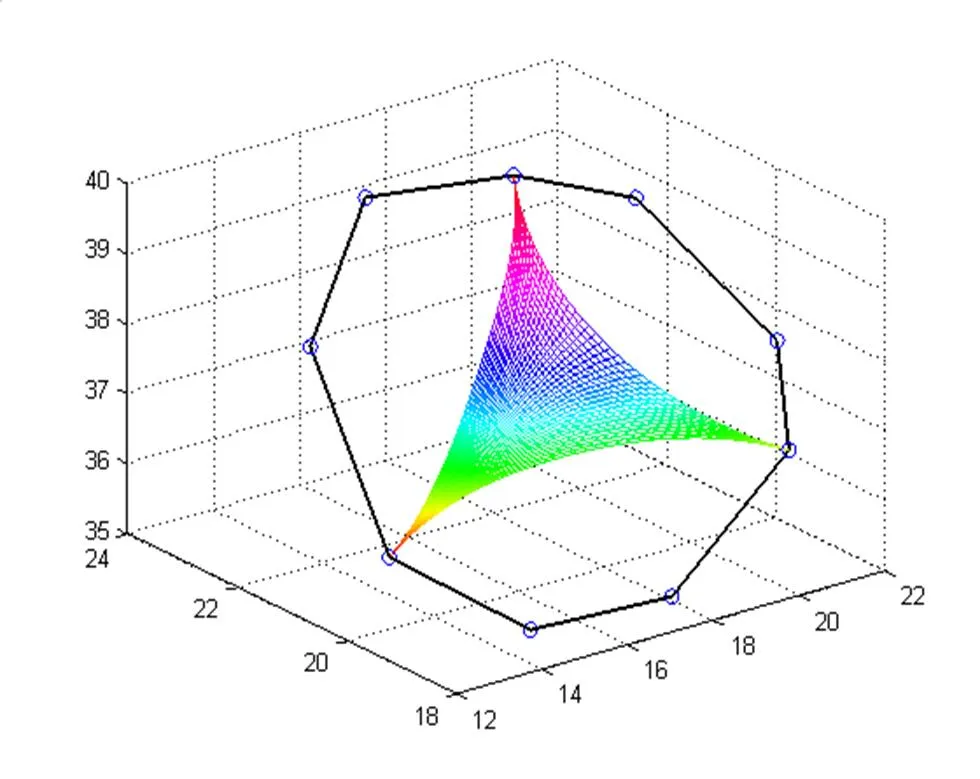
=-1=-0.5

=0.5=1

圖3 單參數值的四次DP曲面片

[3] Chen Jie, Wang Guojin. Construction of triagular DP surface and its application [J]. J. of Computational and Applied Mathematics, 2008, 219(1): 312-326.

[5] Brian A Barsky. Local control of bias and tension in beta-splines [J]. Computer Graphics, 1983, 17(3): 193-218.

[6] Zhang Jiwen. C-curves: an extension of cubic curves [J]. Computer Aided Geometric Design, 1996, 13(3): 199-217.

[7] Chen Qinyu, Wang Guozhao. A class of Bézier-like curves [J]. Computer Aided Geometric Design, 2003, 20(1): 29-39.

[8] 呂勇剛, 汪國昭, 楊勛年. 均勻三角多項式樣條曲線[J]. 中國科學(E輯), 2002, 32(2): 281-288.

[9] Wang Guozhao, Chen Qinyu, Zhou Minghua. NUAT B-spline curves [J]. Computer Aided Geometric Design, 2004, 21(7): 193-205.

[11] Han Xuli.Quadratic trigonometric polynomial curves with a shape parameter [J]. Computer Aided Geometric Design,2002, 19(7): 479-502.

[12] Han Xuli. Cubic trigonometric polynomial curves with a shape parameter [J]. Computer Aided Geometric Design, 2004, 21(6): 535-548.

[13] Han. Xuli.Quadratic trigonometric polynomial curves with local bias [J]. J. Computational and Applied Math, 2005, 180(1): 161-172.

[14] 曹 娟, 汪國昭. 三角域上三次Bernstein-Bézier 參數曲面的擴展[J]. 計算機輔助設計與圖形學學報, 2006, 18(9): 1403-1407.

[15] 吳曉勤, 韓旭里. 帶有形狀參數的Bézier三角曲面片[J]. 計算機輔助設計與圖形學學報, 2006, 18(11): 1735-1740.

[16] 鄔弘毅, 夏成林. 帶多個形狀參數的Bézier曲線與曲面的擴展[J]. 計算機輔助設計與圖形學學報, 2005, 17 (12): 2607-2612.

[17] 于立萍. 三角域上帶兩個形狀參數的Bézier曲面的擴展[J]. 大學數學, 2008, 24(5): 58-62.

[18] 曹莞薔, 汪國昭. 5階三角多項式空間中的擬Bézier 在三角域上推廣[C]//王文平等編. 第四屆全國幾何設計與計算學術會議論文集, 廈門, 2009: 61-67.

Extension of Cubic DP Surfaces over Triangular Domain

WU Xiao-qin, TANG Yun-mei, HAN Xu-li

( 1. School of Mathematics and Computation Science, Hunan University of Science and Technology, Xiangtan Hunan 411201, China;2. School of Mathematical Science and Computing Technology, Central South University, Changsha Hunan 410083, China )

A Class of quartic DP blending functions with two shape parametersis presented, which is an extension of the cubic DP basis functions defined over the triangular domain; Properties of this new blending function are analyzed and the quartic DP parametric surface with two shape parameters over the triangular domain is defined. The surfaces' properties are similar with the cubic DP parametric surfaces. In particular, when the two shape parameters vanish, they degenerate to the cubic DP basis functions and the cubic DP parametric surfaces individually; by changing the two shape parameters, the shape of surface can be adjusted both wholly and locally in invariable control net.

computer application; surface design; DP surface; triangular domain; shape parameter

TP 391.72

A

1003-0158(2011)03-0035-06

2009-10-13

國家自然科學基金資助項目（10871208）；湖南省教育廳科研資助項目（08B027）；湖南科技大學科研啟動金

吳曉勤（1968-），男，湖南懷化人，副教授，博士，主要研究方向為計算機輔助幾何設計，計算機圖形學等。