一種二元有理插值曲面的兩個性質和點控制問題

陸海波1，鄧四清2，方 逵3，謝 進4

?

一種二元有理插值曲面的兩個性質和點控制問題

（1. 湘南學院數學系，湖南郴州423000；2. 韶關學院數學與信息科學學院，廣東韶關 512005；3. 湖南農業大學信息科學技術學院，湖南長沙 410128；4. 合肥學院數理系，安徽合肥 230601）

文獻[22]中已經構造了一種基于函數值的帶參數的二元有理插值樣條，它是分子為雙四次、分母為雙二次的有理樣條。論文研究了該種二元有理插值樣條的有界性，給出了插值的逼近表達式，討論了插值曲面形狀的點控制問題。在插值條件不變的情況下，插值區域內任一點插值函數的值可以根據設計的需要通過對參數的選取修改，從而達到插值曲面局部修改的目的。

二元插值；二元有理樣條；參數；計算機輔助幾何設計

曲線曲面的構造和數學描述是計算機輔助幾何設計中的核心問題。現在已有很多這種方法，如多項式樣條方法、B樣條及非均勻有理B樣條(NURBS)方法、Bézier方法等等。這些方法已廣泛應用于工業產品的形狀設計，如飛機、汽車、輪船的外形設計。通常來說，多項式樣條方法一般都是插值型方法，插值曲線和插值曲面均通過插值點。構造這些多項式樣條，其插值條件除插值點處的函數值外，一般還需要表示方向的導數值。但在很多實際問題中，導數值是很難得到的。同時，多項式樣條方法的一個缺點是它的整體性質，在插值條件不變的情況下，在“插值函數關于插值條件的唯一性”的約束下，無法進行所構造的曲線曲面的整體或局部修改。 NURBS方法和Bézier方法是所謂的非插值型方法，用這些方法所構造出來的曲線曲面一般不通過給定的點，給定的點是作為控制點出現的，通過給定點的變動控制插值曲線曲面的形狀。因此，如果能設計出一種方法，它兼顧以上兩種類型方法的優點，即既是插值型的，又能進行局部或整體修改，同時又是在便于獲取的插值數據下使插值函數具有簡潔的顯示表示，將是非常有意義的。

樣條插值是曲線曲面設計中強有力的工具，十多年來，有理三次插值曲線曲面以及它們在形狀控制中的應用已引起了廣泛的興趣。有理四次插值樣條由于其構造所花費的計算量太大以及在使用上的不方便而讓人們忽視了其重要的應用價值，因此以前很少有人研究它們。但近年來，有理四次插值樣條是比較熱門的研究課題。實際上，在某些情況下有理四次插值樣條有其獨特的應用效果，比如葉懋冬建立的一種具有局部插值性質的分母為二次的有理四次樣條，即一個剖分子區間上的有理插值式只與鄰近區間上的插值點有關，一個插值節點上的數值變動只影響其鄰近的局部范圍；閔杰等構造了一種分母為線性的有理四次插值樣條，研究得到了該種有理四次插值樣條不但具有三次多項式的插值精度而且具有獨特的逼近性質；Wang等先構造了一種有理四次插值樣條，討論了插值樣條的保單調性、連續性以及逼近性質，然后將其推廣到有理雙四次插值曲面；張彩明等討論了連續的四次樣條曲面插值。鄧四清等研究了一種空間曲面插值問題，給出一種新的矩形分劃上的僅基于函數值的分片二元有理插值樣條的構造方法，每片中帶有關于方向兩個參數和關于方向的兩個參數，是分子為雙四次、分母為雙二次的有理函數；導出了關于插值曲面的光滑性定理，該定理指出，當選取其中關于方向的兩個參數滿足一定條件時，插值曲面在插值區域光滑。更有趣的是，當關于方向的兩個參數滿足某種條件時，插值函數可表示為矩陣形式，并且這種表示具有對稱性，最后還討論了插值基函數的性質。該文研究了此種二元有理插值的邊界性質和點控制問題。證明了無論參數取何正值，在給定的插值區域內插值函數均有界，稱之為插值有界性。同時，給出了插值的逼近表達式，且表達式與參數無關。在給定插值數據不變的條件下，選擇適當的參數可于插值區域內修改任意點插值函數值，可將此應用于在實際設計中，不改變插值數據而修改插值曲面。

1 插值函數的構造

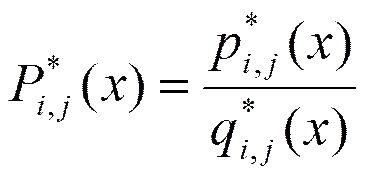
此處

且

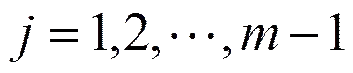
此處

且

2 插值基函數

本文的如下部分，作者總假定分劃是等距的，即考慮矩形插值域上的等距矩形分劃，即對所有的和，有，記之為，且，記之為。對任一和所有，假設常數且=常數，分別記之為與，對任一，假設另一組參數，對所有的亦分別為常數，分別記之為，。于是由文獻[22]知，由式（1）定義的插值函數可以表示為

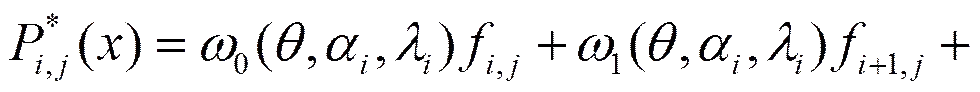
其中

（4）

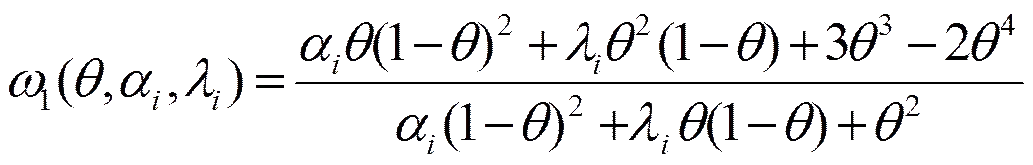
（6）

且

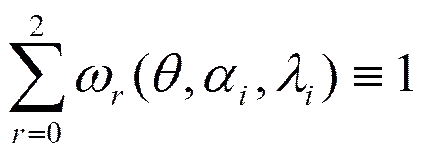
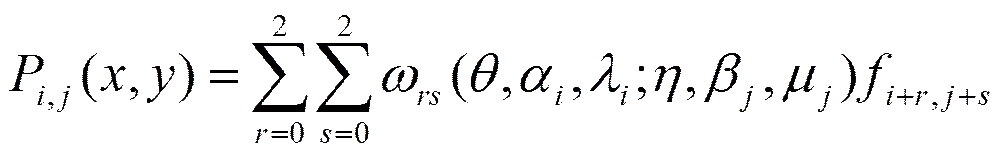
這里

（8）

且

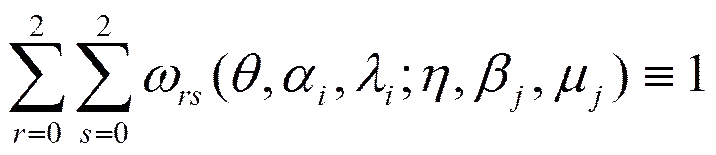
3 插值函數的有界性及逼近性質

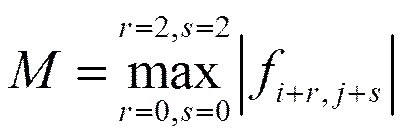
證 明 由式（7）和式（8）得

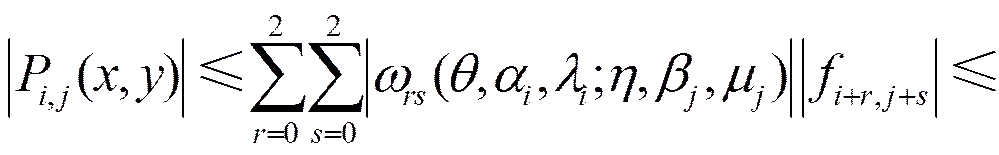
（10）

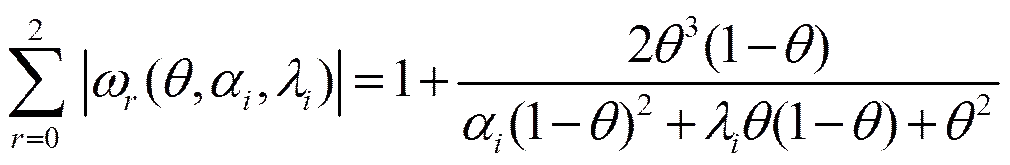
同理可得

（12）

令

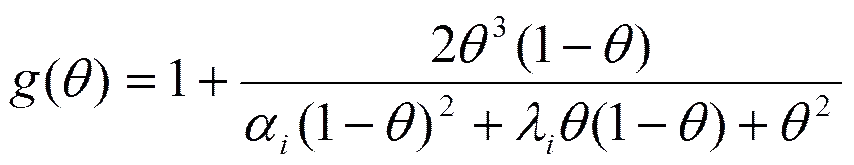
又

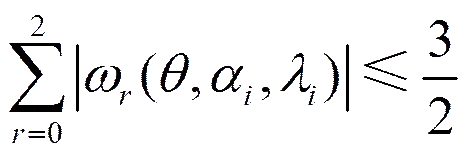
（14）

從而由式（10）知

即定理的結論成立。

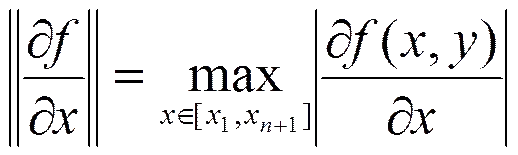
于是有

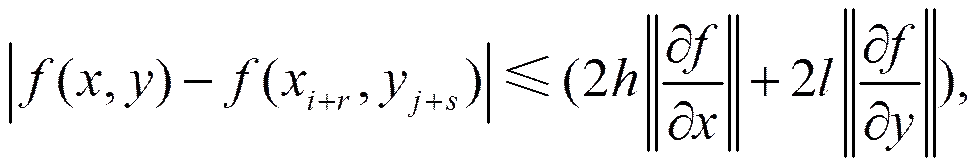
由式（7）和式（9），得

于是有

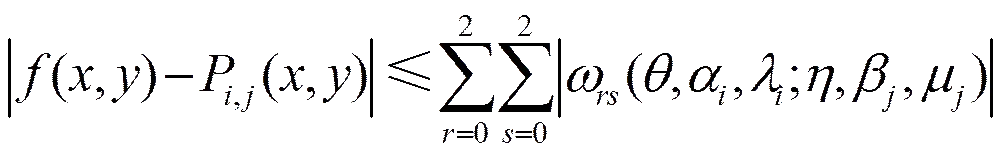
從而由式（13）及式（14），有如下的逼近定理：

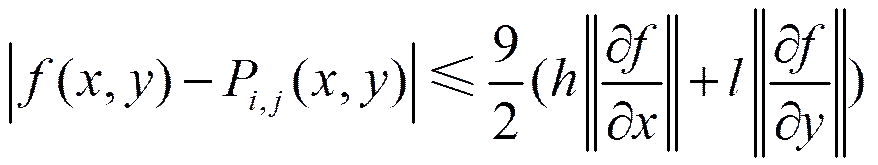
4 插值的中央點控制

一般而言，在插值區域內，插值曲面的形狀依賴于插值數據。由于插值的唯一性，若插值數據給定，則插值曲面的形狀便固定。但是，對于由式（2）所定義的插值，因其含有參數，故在插值數據不變的情況下，當參數變化時插值函數也隨之變化。因此，插值曲面隨參數改變而改變。基于此特點，通過選擇適當的參數能夠修改插值曲面的形狀。

令

所以

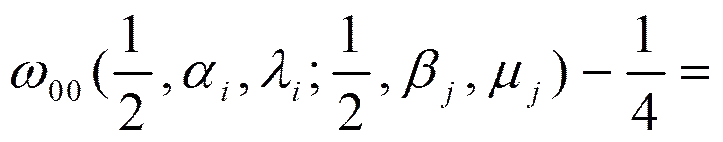
（17）

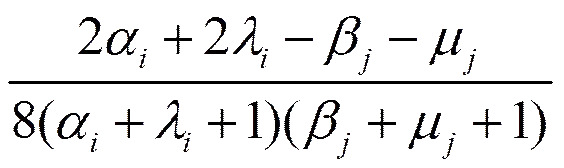
（19）

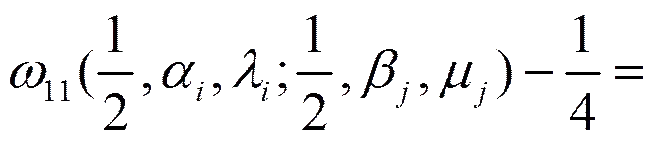
（20）

（22）

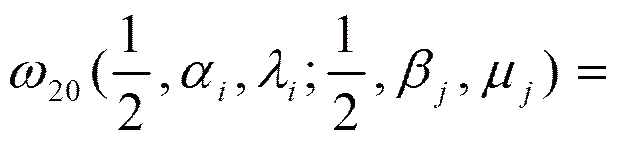
（23）

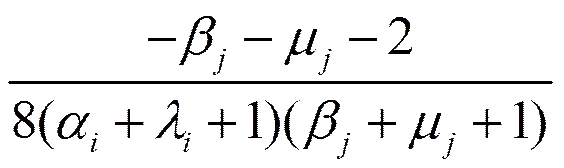
（25）

將式（17）~式（25）代入式（16），并整理得

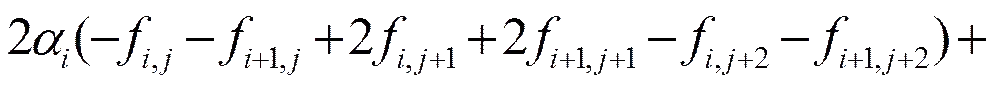
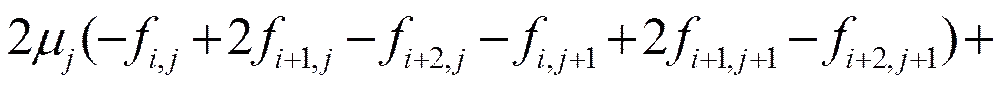
（26）

記

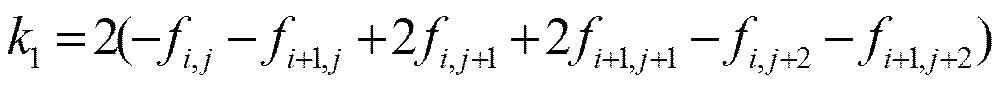
則式（26）變為

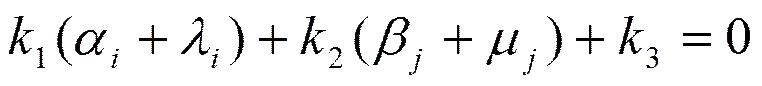
定理3 “中央點－平均值”控制問題有解的充分條件是方程式（27）存在正參數解，，和。

5 結束語

對二元插值而言，通過插值數據確定插值函數表達式的邊界值非常困難，而得到二元插值函數誤差估計的表達式更為困難，這兩個問題該文分別由定理1和定理2圓滿解決。此外，該文還建立了中央點控制的方法，對任意給定的實數，由式（16）可以衍生出多種不同的表達式，因此，通過“中央點－平均值”控制問題的解決，同樣也可以得到多種控制的方案。

[1] Farin G. Curves and surfaces for computer aided geometric design: a practical guide [M]. Academic press, 1988. 28-54.

[2] Foley T A. Local control of interval tension using weighted splines [J]. Computer Aided Geometric Design, 1986, 3(2): 281-294.

[3] Bézier P E. The mathematical basis of the UNISURF CAD system [R]. Butterworth, London, 1986.

[4] Dierck P, Tytgat B. Generating the Bézier points of-spline curve [J]. Computer Aided Geometric Design, 1989, 6(2): 279-291.

[5] Piegl L. On NURBS: a survey [J]. IEEE Computer Graphics and Application, 1991, 11(1): 55-71.

[6] Nielson G M. CAGD’s Top Ten: What to watch [J]. IEEE Computer Graphics and Automation, 1993, 13(1): 35-37.

[7] Kouichi Konno, Hiroaki Chiyokura. An approach of designing and controlling free-form surfaces by using NURBS boundary gregory patches [J]. Computer Aided Geometric Design, 1996, 13(4): 825-849.

[8] Laurie M Wilcox. First and second contributions to surface interpolation [J]. Vision Research, 1999, 39: 2335-2347.

[9] Lin R S. Real-time surface interpolator for 3D parametric surface machining on 3-axis machine tools [J]. Machine Tools and Manufacture, 2000, 40: 1513-1526.

[10] Jiang D H, Liu H N, Wang W G. Test a modified surface wind interpolation scheme for complex terrain in a stable atmosphere [J]. Atmospheric Environment, 2001, 35: 4877-4885.

[11] Peter Comninos. An interpolating piecewise bicubic surface with shape parameters [J]. Computer and Graphics, 2001, 25(4): 463-481.

[12] Rainer Müller. Universal parametrization and interpolation on cubic surfaces [J]. Computer Aided Geometric Design, 2002, 19(4): 479-502.

[13] Duan Qi, Djidjeli K, Price W G, et al. A rational cubic spline based on function values [J]. Computer and Graphics, 1998, 22(4): 479-486.

[14] Duan Qi, Wang L, Twizell E H. A new bivariate rational interpolation based on function values [J]. Information Sciences, 2004, 166: 181-191.

[15] Duan Qi, Zhang Yunfeng, Twizell E H. A bivariate rational interpolation and the properties [J]. Applied Mathematics and Computation, 2006, 179: 190-199.

[16] Duan Qi, Zhang Huanling, Zhang Yunfeng, et al. Bounded property and point control of a bivariate rational interpolating surface [J]. Computers and Mathematics with Applications, 2006, 52: 975-984.

[17] 葉懋冬. 關于具局部插值性質的樣條[J]. 計算數學, 1984, 6(2): 138-147.

[18] 閔 杰, 陳邦考. 一種四次有理插值樣條及其逼近性質[J]. 高等學校計算數學學報, 2007, 29(1): 57-62.

[19] Wang Qiang, Tan Jieqing. Rational quartic spline involving shape parameters [J]. Journal of Information and Computational Science, 2004, 1(1): 127-130.

[20] Wang Qiang, Tan Jieqing. Shape preserving piecewise rational biquartic surfaces [J]. Journal of information and Computational Science, 2006, 3(2): 295-302.

[21] 張彩明, 汪嘉業.連續的四次樣條曲面插值[J]. 中國科學(E輯), 2003, 33(2): 116-126.

[22] 方 逵, 鄧四清, 謝 進, 等. 一種新的二元有理插值及其性質[J]. 工程圖學學報, 2010, 31(4): 116-122.

Two Properties and Point Control of Bivariate Rational Interpolating Surface

LU Hai-bo, DENG Si-qing, FANG Kui, XIE Jin

( 1. Department of Mathematics, Xiangnan University, Chenzhou Hunan 423000,China;2. School of Mathematics and Information Science, Shaoguan University, Shaoguan Guangdong 512005, China;3. School of Information Science and Technology, Hunan Agricultural University, Changsha Hunan 410128, China;4. Department of Mathematics and Physics, Hefei University, Hefei Anhui 230601, China )

A bivariaterational interpolation spline with parameters was created in an earlier work which was based on function values only, and this spline is a rational one with biquartic numerator and biquadratic denominator. This paper discusses the spline’s boundary property, the approximation expression of the interpolation and the point control method of the interpolating surface. It is proved that the values of the interpolating function in the interpolation region are bounded no matter what the parameters might be, which is called the boundary property of the interpolation. Also, the approximation expression of the interpolation are derived, which does not depend on the parameters. More important is that the values of the interpolating function at any point in the interpolating region can be modified under the condition that the interpolating data are not changed by selecting the suitable parameters, so the interpolation surface can be modified for the given interpolation data when needed in practical design.

bivariate interpolation; bivariate rational spline; parameter; computer aided geometric design

TP 391；O 241.3

A

1003-0158(2011)03-0028-07

2008-10-13

國家自然科學基金資助項目（60773110）；湘南學院科研資助項目（2010Y060）；湖南省科技計劃資助項目（2008FJ3046）；韶關學院校級重點扶持學科建設項目；湖南省高校科技創新團隊計劃支持項目；安徽省教育廳自然科研資助項目（KJ2008B250）

陸海波（1962-），男，湖南耒陽人，副教授，主要研究方向為計算機輔助幾何設計。