圓柱滾子軸承滾道圓度誤差對旋轉精度的影響

宋飛，李濟順,2，劉永剛,2

(1.河南科技大學 機電工程學院，河南 洛陽 471003；2.河南省機械設計及傳動系統重點實驗室，河南 洛陽 471003)

滾動軸承的旋轉精度是表征其質量的一個主要指標，既影響軸承運轉時的工作性能，也反映了軸承的制造精度[1-2]。為了提高軸承的旋轉精度，軸承行業從控制軸承零件工作表面的幾何誤差著手，提升零件的制造精度，并取得了顯著的成果[3-5]。對于圓柱滾子軸承，其零件的圓度和圓柱度等可以采用3點法誤差分離技術和提純技術進行精密測量和重構[6-9]。利用GPS標準的數字化計量方法，可以對圓度、圓柱度的誤差進行評定[10-12]。圓柱滾子軸承的內圈、外圈、滾子和保持架等都有其自身的精度，各自精度的差異和運動副間隙及其相互作用必定影響成品軸承的旋轉精度，然而在這方面的研究較少，尤其關于軸承零件的幾何精度與旋轉精度之間的關系方面更是鮮見報道。下文以圓柱滾子軸承為研究對象，在軸承零件形狀誤差研究的基礎上，分析滾道圓度誤差對旋轉精度的影響，為建立圓柱滾子軸承旋轉精度的預測和評價體系，設計和開發高精度圓柱滾子軸承提供理論支持。

1 數學模型的建立

1.1 基本假設

(1)滾子、套圈在軸承徑向平面內做平面運動，內圈有3個自由度,分別為徑向平面內兩垂直方向的平移和繞自身軸線的轉動。

(2)外圈固定，滾子為純滾動，滾子與外圈滾道完全接觸，內圈以恒定的角速度旋轉。

(3)不考慮彈流潤滑條件，不計其他形狀誤差(外圈滾道圓度誤差、滾子的圓柱度誤差等)對旋轉精度的影響。

1.2 內圈滾道圓度誤差簡化

內圈圓度誤差可以表示為Fourier級數形式

(1)

式中：θ為內圈滾道的角度變量；N為圓度誤差諧波分量的最高階數；An和Bn分別為內圈滾道圓度誤差第n階諧波分量的余弦項和正弦項系數。

為簡化計算，內圈滾道曲線形狀可以用標準圓和Fourier級數的諧波分量表示，如圖1所示，則滾道曲線在直角坐標系下的參數方程為

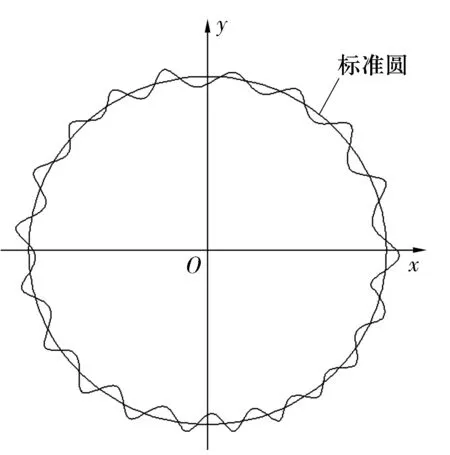
圖1 內滾道圓度誤差簡化

(2)

式中：F為內圈滾道直徑；R(θ)為Fourier級數的諧波分量。

1.3 建立坐標系

為了能方便地描述軸承及其零件的運動，將圓柱滾子軸承放在設定的坐標系中進行分析。根據圓柱滾子軸承的特點，建立整體坐標系(x，y，z)和內圈的局部坐標系(xr，yr，zr)，在整體坐標系中，z軸沿軸承軸線方向，x-y面與軸承滾道的徑向平面重合，如圖2所示。

圖2 坐標系系統

坐標變換的一般形式為

(3)

式中：φ為內圈轉過的角度；δx，δy為內圈圓心相對于軸心的變化量。

1.4 軸承各零件的幾何關系

根據運動幾何關系得

(4)

式中：α為滾子繞軸線轉過的角度；Dpw為滾子組節圓直徑；Dw為滾子直徑。

第i(i=1，2，…，Z)個滾子圓心的坐標為

(5)

滾子圓心到內圈滾道曲線的距離為

(6)

2 數值仿真與模擬

通過建立的數學模型，對圓柱滾子軸承的運動狀態進行數值仿真與模擬，程序流程圖如圖3所示，實現的步驟如下。

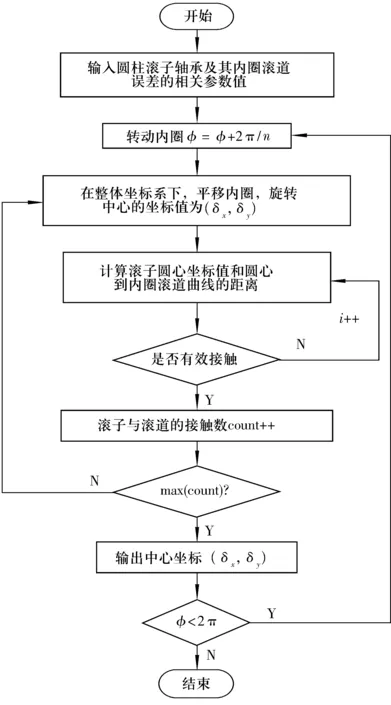
圖3 程序流程圖

(1)設定相關參數。根據軸承設計手冊查得圓柱滾子軸承零件的參數值，比如內徑、外徑和徑向游隙等。在整體坐標系下，設定內圈的轉動步長為h=2π/n(n為正整數)，則轉過的角度為φj=jh(j=1，2，…，n)，取Fourier級數的諧波分量為R(θ)，滾道的圓度誤差用Fourier級數的諧波分量表示。根據 (2)～(5) 式和已知的參數值，可以得到滾道曲線在整體坐標系下的參數方程及滾子的圓心坐標值。

(2)運動仿真。在不考慮載荷作用的情況下，外圈固定，滾子為純滾動，內圈按設定的步長轉動，內圈每轉動一個步長，沿坐標軸方向平移內圈，平移步長為Δx，Δy，旋轉中心相對于整體坐標系原點的變化量為δx，δy，分別計算每個滾子圓心到內圈滾道曲線的距離，進而判斷滾道與滾子的接觸情況。

(3)判斷有效接觸及滾子接觸數。若滾子圓心到滾道曲線的距離與滾子的半徑之差在允許的誤差范圍內(如圓度誤差值的1%)，可認為是有效接觸，由力學平衡條件可知，滾子和套圈至少有兩點接觸時才能處于平衡狀態，在內圈的平移量內，分別記下滾道與滾子的接觸數m≥2的中心坐標值，在內圈轉動的一個步長內，輸出有效接觸數最大值及對應的旋轉中心坐標值(δx,δy)。內圈轉動一周即可得到一系列的坐標值(δx1,δy1)，(δx2,δy2)，…，這些中心坐標點所在的區域即為內圈旋轉中心的取值范圍。

3 計算示例

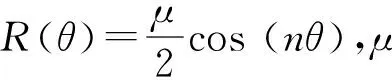
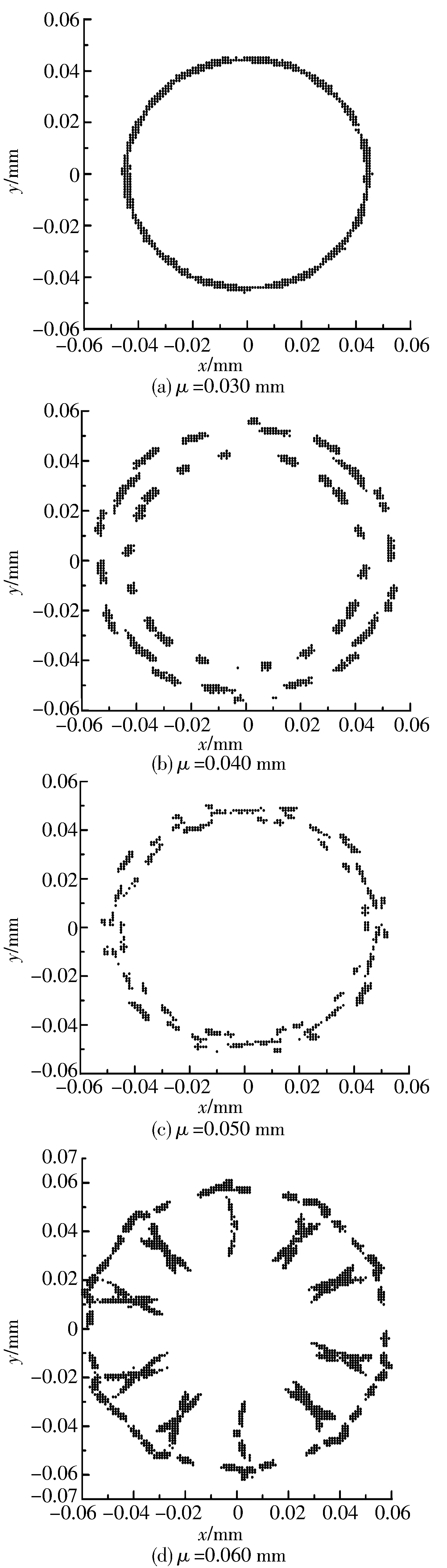
圖4 內圈滾道不同的圓度誤差對應的旋轉中心坐標

表1 軸承的計算參數

由不同圓度誤差的旋轉中心分布特點可知，隨著圓度誤差的增大，中心坐標點分布擴散，內圈旋轉中心的振動幅值增大，在轉動過程中軸承零件的形狀誤差越大，產生的振動特性越明顯，計算結果與實際情況比較吻合。對不同圓度誤差對應的內圈旋轉中心的最大幅值進行曲線擬合，從圖5可以看出，隨著內圈滾道圓度誤差的增大，內圈旋轉中心的幅值增大，旋轉精度降低，圓度誤差越大，旋轉中心幅值上升趨勢越平緩。由此可以推斷，在徑向游隙的范圍內，旋轉中心的最大幅值會隨滾道圓度誤差的增大而達到某一極限值。

圖5 不同圓度誤差對應的旋轉中心幅值

4 結論

(1)軸承零件的圓度誤差是影響其旋轉精度的一個重要因素，根據不同圓度誤差的旋轉中心分布特點及規律，可以有效地預測軸承的旋轉精度。

(2)滾道的圓度誤差越大，旋轉中心的幅值變化越明顯，在徑向游隙的范圍內，旋轉中心的最大幅值隨滾道圓度誤差的增大將達到某一極限值。