高層建筑抗震計算數值方法分析

周清橋

0 引言

結構的抗震計算分析方法有很多，本文根據高層建筑結構的特點，對其進行抗震計算分析。

1 計算模型

多層結構往往采用層剪切模型來計算。而像更高層數的結構，其結構往往是筒體或框架剪力墻結構，則適合采用彎剪層模型。而桿模型以梁、柱等單根構件為基礎單元，將樓層質量分別集中于結構各節點，形成質點。桿模型是較為精確的計算模型，我們采用的計算模型是層剪切模型，其方程如下［1］:

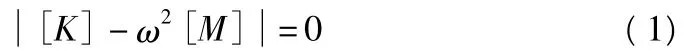
2 數值計算方法

2． 1 結構非線性計算方法

式(1)是非線性方程，需要用數值方法求解。但這里我們采用比較有代表性的Newton-Raphson法，在進行非線性求解時具體采用增量Newton-Raphson方法，此方法是先把荷載分成若干增量(或荷載步)，然后在每個增量步內用Newton-Raphson方法進行迭代求解。

圖1是增量Newton-Raphson方法求解非線性方程F=Kδ的圖解。圖1中荷載 F 分成了 i個增量步(F1，F2，…，Fi-1，Fi)，現以第一增量步為例說明Newton-Raphson方法的迭代過程。在直角坐標系F—δ中，第一增量步內直線F1=R和曲線F=Kδ的交點A的橫坐標δA就是方程F=Kδ在第一增量步內的解。

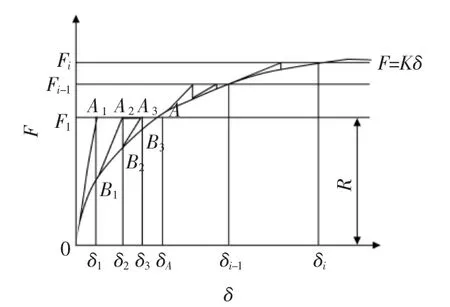
圖1 增量Newton-Raphson方法

在實際使用中，Newton-Raphson法開始需先按線性理論求出位移δ1作為第一次迭代近似值，即圖1中A1點的橫坐標，如果荷載R并不因變形而改變它的數值和方向(假設為小變形)，則得［2］:

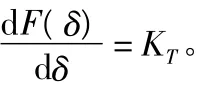
其中，KT為曲線F=Kδ的斜率(或切線剛度)。

第二次迭代從B1點做曲線F=Kδ的切線交直線F1=R于A2點，取A2點的橫坐標δ2，從圖1中可見:

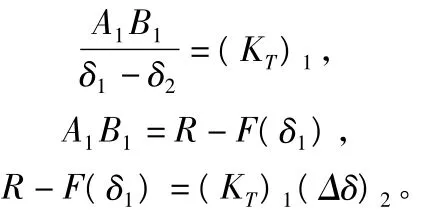
由圖1看出δ2就是位移的第二次迭代近似值。如此重復可得以下迭代公式:

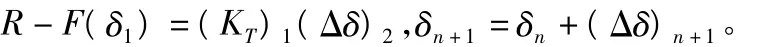
不斷重復迭代直至滿足收斂條件為止，便可得到最終結果。其他增量步內的求解過程與第一增量步內相同，實踐證明該法收斂性較好。

2． 2 矩陣特征值與特征向量的求解

對結構進行振型分析，求特征值:

注意到式(1)并不是標準的特征值表達式，可采用矩陣運算的方法把式(1)化為標準的特征值表達式。

在式(1)左右同時乘以［M-1］，即可化為:

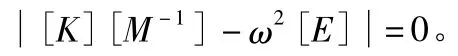
令 A=［K］［M-1］，λ =ω2，式(1)即可變成標準的特征值表達式。這里［E］為單位剛度矩陣。

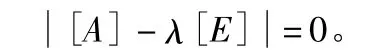
當然也可以左右同時乘以柔度矩陣［K-1］，兩者是等效的。

上式問題常用的解法有雅可比法、迭代法以及近年來發展的子空間迭代法，此處采用的方法屬于迭代法求解。由于總剛矩陣［A］并不是實對稱矩陣，不適用雅可比法，而須先把其化解為赫申伯格矩陣，然后用QR方法來求解其特征值。

1)約化赫申伯格步驟，對k=2，3…作如下變換:

a．從第k-1列的第一個以下的元素中選出絕對值最大的元素 al，k-1。

b．交換第l1行與第k行，交換第l1列與第k列。

c．對于 i=k+1，…，n 作變換:

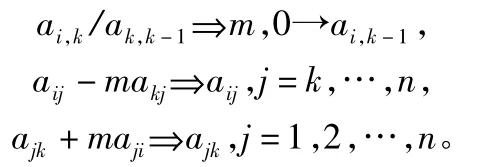
2)求赫申伯格矩陣全部特征值的QR方法步驟:

設不可約的上H矩陣為A。

a．確定一個初等正交矩陣Q0:

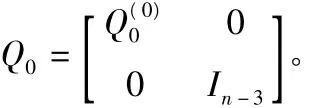
對A作相似變換A1=Q0AQ0。

b．利用同樣的方法確定正交對稱矩陣 Q1，Q2，…，Qn-2，對A1，A2，…，An-2作相似變換:

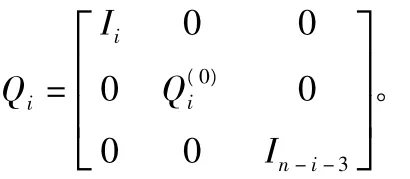
反復進行以上迭代，直到將上H矩陣A變為對角塊全部是一階塊或二階塊為止，此時就可以直接從各一階塊或二階塊解出全部特征值。

3)求特征矩陣的特征向量:

利用求得的特征值代入特征方程，采用全選主元消去法的步驟:

設方程為AX=B。

消去過程:

a．全選主元。即從系數矩陣的第k行、第k列開始的右下子陣中選取絕對值最大的元素，并將它交換到主元素的位置上。

b．歸一化。即:

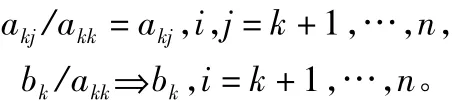
c．消去。即:

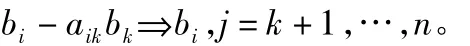
回代過程:

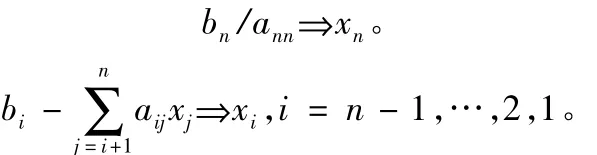
2． 3 結構動力非線性分析的Newmark-β方法

在結構動力非線性分析中，本文使用Newmark-β時間積分方法，在離散的時間點上求解這些方程，在tn+Δt時刻，動力方程式為:

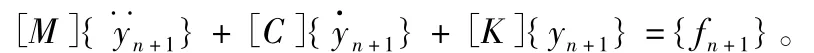
其中，［M］，［C］，［K］分別為質量矩陣、阻尼矩陣和剛度矩陣;{}，}，{y}分別為加速度矢量、速度矢量和位移n+1矢量;{fn+1}為作用力矢量。

主要計算步驟:

1)初始計算。

b．選擇時間步長 Δt，參數 β，γ，計算積分常數。

c．形成等效剛度矩陣［⌒K］=［K］+a0［M］+a1［C］。

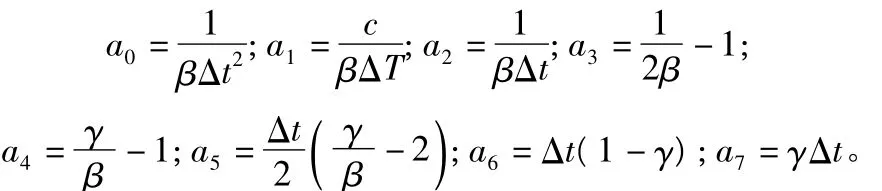
2)對每一時刻計算。

a．計算t+Δt時刻等效荷載:

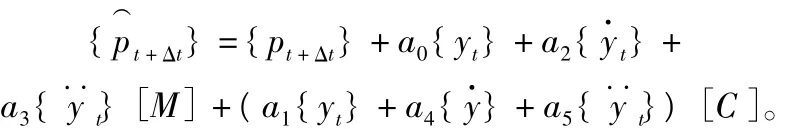
c．計算t+Δt時刻的加速度和速度:

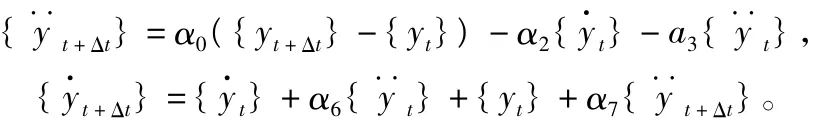
在Newmark-β法中，參數β，γ的取值影響著算法的精度和穩定性，且迭代的步長決定迭代的收性。為保證算法具有不低于二階精度，要求參數β取值為1/2;一般情況下，參數γ取1/8～1/4即可獲得穩定的解。本文中 β取1/2，γ取1/4，為有條件穩定［3，4］。

3 計算結果

以某12層框架結構為例，因為其樓層較低，其抗側力構件薄弱，且層數較低，因此結構的計算模型采用層間剪切模型。鑒于計算結果的工程判斷以模型的層間剪力和層間位移為主，通常以等效層間模型為主要的分析模型，其結果與用桿單元的計算模型精度相差不超過5%。在選用場地波形方面，我們選用最不利波El-Centro波。而El-Centro波計算時原結構的位移反應最大。El-Centro波為振動型破壞地震波。Taft波為沖擊型破壞地震波。人工隨機波為能量型地震波。地震波對結構的作用自然應該首先體現在振動型破壞作用上。為了分析共振效應，我們進一步分析了El-Centro波，下面我們列出這El-Centro波的傅立葉譜，見圖2。

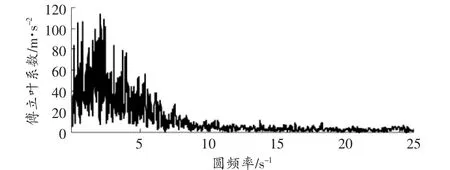
圖2 El-Centro E-W傅立葉譜

經過分析各條波的傅立葉譜，我們發現各條波的卓越圓頻率段為:El-Centro E-W波—0 s-1～3．75 s-1。以上四條波都將波峰集中在結構的圓頻率附近，所以易發生共振［5］。

［1］ 張 敏．高層框架動力分析剛度矩陣的彎剪層模型［J］．華東交通大學學報，2005，22(5):34-36．

［2］ 鐘萬勰，何 窮，劉正興．數值計算方法［M］．北京:中國建筑工業出版社，1991:130-138．

［3］ 沈聚敏，周錫元．抗震工程學［M］．北京:中國建筑工業出版社，2000:1-299．

［4］ 呂西林．高層建筑結構［M］．武漢:武漢工業大學出版社，2001:44-50．

［5］ 李 輝，曹 亮．在役結構的抗震分析［J］．浙江工業大學學報，2005，33(2):223-226．