基于拓展OWA算子的商業銀行服務質量評價

杜建國，王冰潔，黃后慶

（1.江蘇大學工商管理學院，江蘇鎮江212013;2.南京大學工程管理學院，南京210093）

0 引言

商業銀行作為服務性企業，提供高質量的服務是贏得核心競爭力的關鍵。高質量的服務可以影響客戶的價值觀和客戶滿意度，而客戶的滿意度又直接影響客戶的忠誠度[1]。然而服務的抽象性、無形性和異質性等特性使得服務的定量分析變得復雜。銀行服務同樣面臨著定量分析的困難，其核心問題是服務質量的測定[2]。國內外很多學者對銀行服務質量進行研究，如Athanassopoulos(1997)、Karatepe et al(2007)、陳瑩等(2008)、金文姬(2007)等通過研究影響銀行服務質量的各種因素，分別構建了銀行服務質量的評價指標體系。

從研究方法上看，目前關于評價服務質量的方法很多，如結構方程模型、多元統計等統計方法、數據包絡法(DEA)、網絡分析法(ANP)等。銀行服務質量指標的不易被量化使得評價具有一定程度的模糊性，以及評價過程中評價者受各種因素影響可能會做出過高或過低的不公正評價，都會影響最終的評價結果。針對這類問題，本文將模糊理論與DUOWA算子進行整合，可以很好的解決此類問題。模糊理論以隸屬函數來表達模糊不確定的知識，可有效地對專家評估數據進行處理。DUOWA算子是拓展的OWA算子，其特點是可以用于區間數的計算，同時近似度的引入可降低評估結果受極端評估數據的影響。兩種方法的整合可準確地得到銀行服務質量評價結果，具有一定的實用價值。

1 模糊理論

Zadeh(1965)提出模糊集合理論(Fuzzy Logic)，以處理概念模糊不確定的事物為主要研究目標[3]。模糊集合是對普通集合的延伸，允許中間狀態的存在。針對過于復雜或難以定義的情況，傳統量化表達方式很難合理描述，Zadeh(1975)提出用模糊語義代替[4]。本研究即采用三角模糊數表達模糊信息，三角模糊數與模糊語義的關系見表1。

本研究引入模糊集的α截集的概念,α={|α α∈(0,1)}。假設某三角模糊數為[aL,aM,aU]，可用區間[bL,bU]表達。其中，

采用Facchinetti(1998)提出的解模糊數方法將三角模糊數轉換成明確值，解模糊化公式：

2 拓展OWA算子

Yager(1988)年提出集成離散數據的有序加權平均(OWA)算子[5]，其主要特點是：對一組評估數據從大到小進行排序后加權集成，其權重只與相應的位置有關。

定義1：設OWA:Rn→R，若

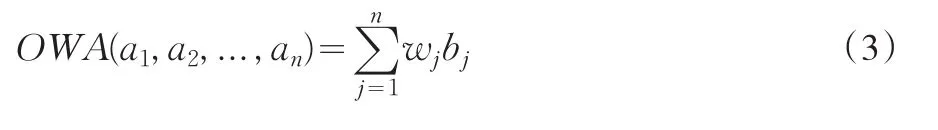
其中：R為實數集，w=(w1,w2,...,wn)T是與OWA函數相關聯的加權變量，wj∈[0,1],1≤j≤n，wj只與第j個位置有關，與aj無關，且bj是(a1,a2,...,an)中第j個最大的元素。OWA算子只能用于明確值的計算，不能用于區間計算。針對不確定環境，Xu和Da(2002)提出了不確定加權平均算子和相關不確定有序加權平均，該算子按照評價者的評估數據情況決定相應的位置權重，可確保評估結果不會受到部分極端評價的影響[6,7]。

定義2：設UOWA:Ωn→Ω ，若：

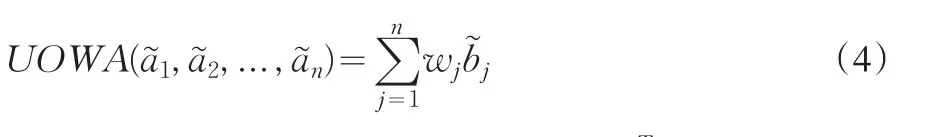
其中：Ω為實數集，w=(w1,w2,...,wn)T是與UOWA函數相關聯的加權變量，是中第j個最大的元素，為區間數。

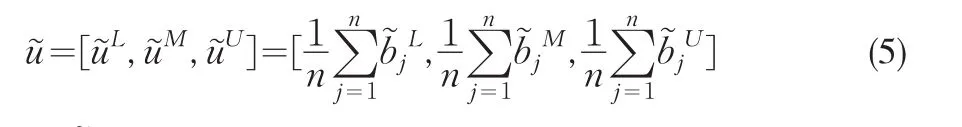
表1 三角模糊數

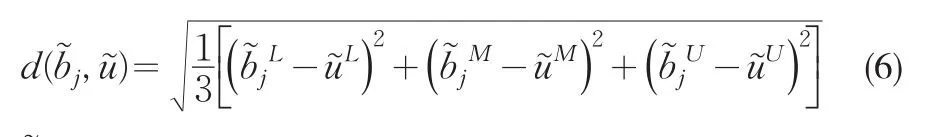
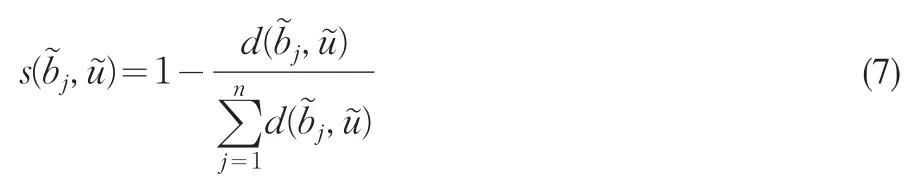
定義4：UOWA函數的加權變量[7]計算為：

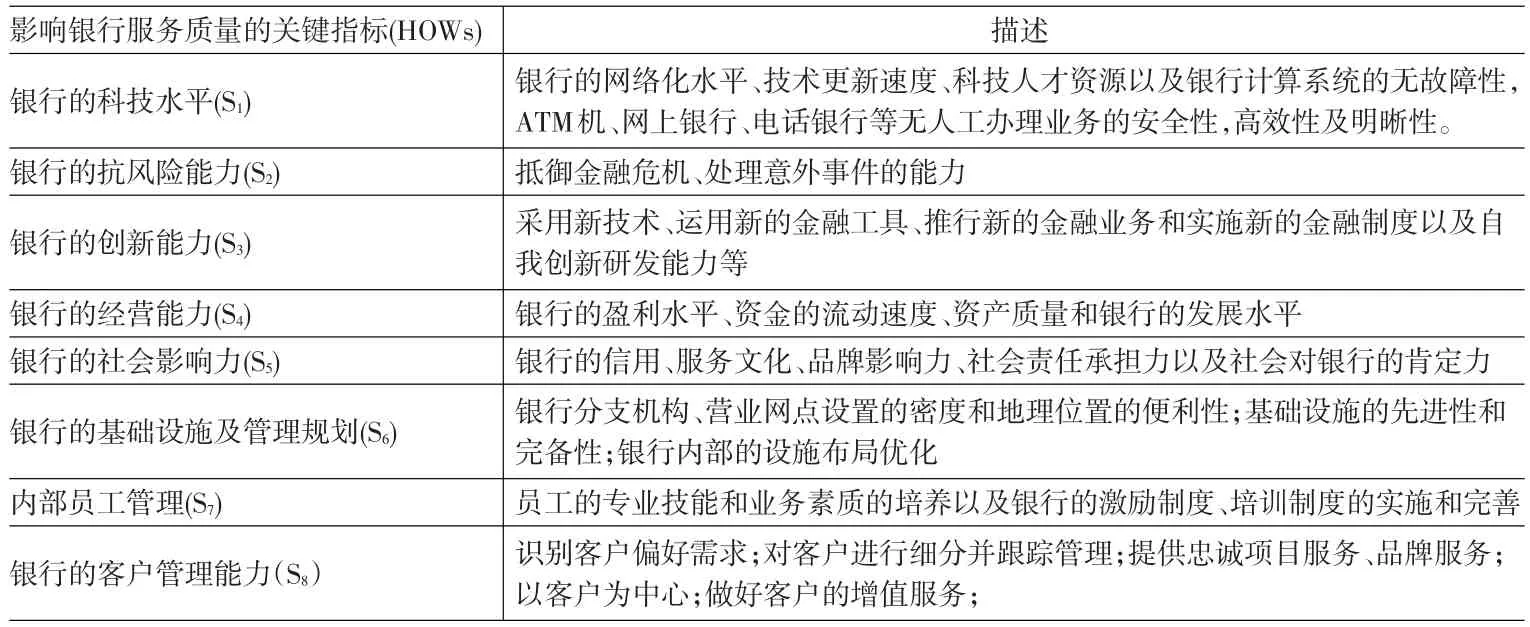
表2 影響商業銀行服務質量的關鍵指標

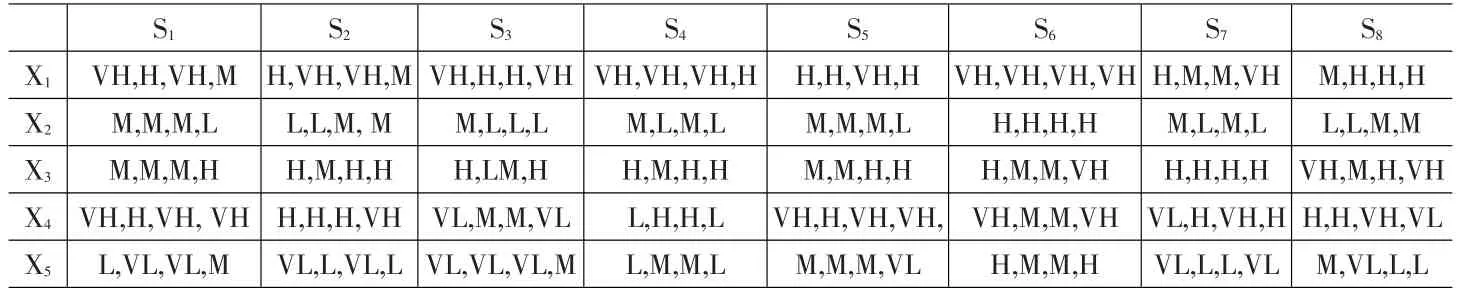
表3 銀行服務質量的原始評估數據

其中，wj表示第j個位置的權重大小，即第j個相似度占所有相似度的比例。wj∈[0,1]且

根據公式(4)和(8)，可得到UOWA值的計算公式[7]為：

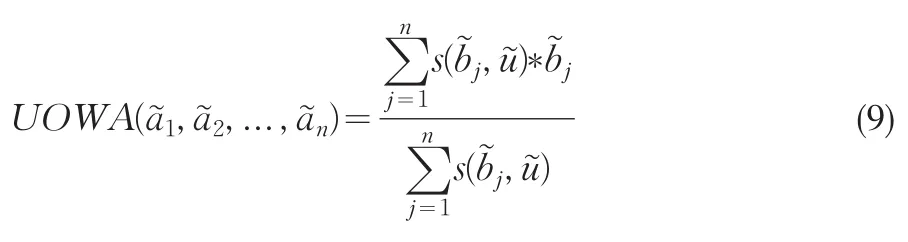
其中，bj是(a1,a2,...,an)中第j個最大的元素。

3 實證分析

某商業銀行為提高自身服務競爭力，組織多位專家對本銀行以及周圍4家主要競爭對手的服務質量進行評估。通過對比評估結果，找出自身服務的劣勢并采取有效措施，達到提高服務水平的目的。本研究在現有研究基礎上，結合實際情況建立了影響銀行服務質量的8個關鍵指標，如表2。

假設評價者集為D={d1,d2,d3,d4}，影響銀行服務質量的8個關鍵指標集為S={S1,S2,S3,S4,S5,S6,S7,S8}，四位專家通過模糊層次分析法確定8個關鍵指標的權重向量為wS=(0.14,0.07,0.06,0.11,0.06,0.17,0.20,0.19)，評價采用模糊語義進行評價，得到原始評價矩陣，如表3。

所有的評估數據均轉換成三角模糊數，通過將各個指標的評估數據與指標權重進行加權，可得到4個評價者對5家銀行的總體服務質量評價區間，如表4。

應用公式(9)，對每家銀行的4個評價區間進行處理，可得到5家銀行最終的UOWA值。設α=0.5，應用公式(1)將三角模糊數轉換成近似區間。應用公式(2)進行解模糊化處理，可到最終的銀行服務質量排序，結果如表5。

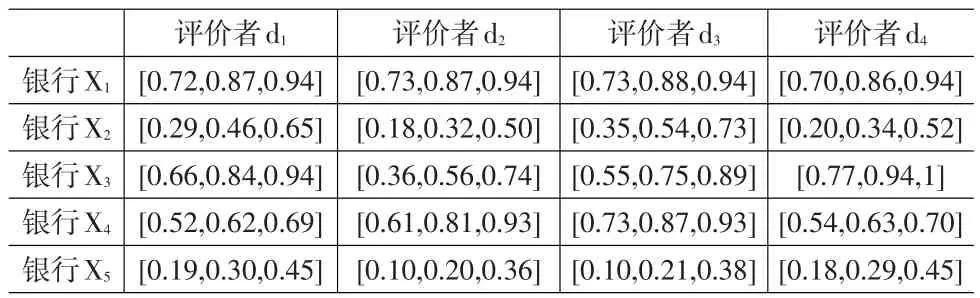
表4 四位評價者對五家銀行的服務質量評價矩陣

應用公式(10)，建立5家銀行服務質量的區間概率比較矩陣，如下：

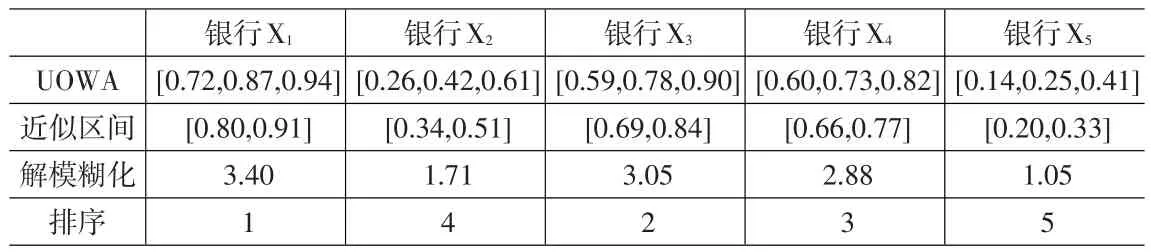
表5 五家銀行的服務質量評價結果及排序

對P矩陣的各行進行橫向累加，得到5家銀行服務質量評 價 的 P值 ：p1=4.3429;p2=1.5;p3=2.9940;p4=2.8370;p5=0.5，排序為：p1≥p3≥p4≥p2≥p5。

通過比較UOWA值和P值排序，得出了同樣的排序結果，即第一家銀行的服務質量總體水平最高，排序為：X1≥X3≥X4≥X2≥X5。排序在前的銀行在權重較大的關鍵指標上的得分相對較高，是這幾家銀行總體服務質量較高的主要原因。

4 結論

模糊理論和拓展OWA算子的整合應用在服務質量的測定方面有著一定的優勢。本研究采用三角模糊數對專家評估數據進行處理避免了信息流失，可最大程度表達出評估者的偏好；DUOWA算子的應用不僅避免了OWA算子不能解決區間值以及運算結果不具有封閉性等問題，而且近似度的引入也確保評估結果不受極端評估數據的影響。兩種方法的結合能夠準確地評價出銀行服務水平，并能避免主觀臆斷和個別不公正評價對評價結果的影響。

銀行的服務質量改進是一個持續改進的過程，同時也是銀行提高競爭力的一個重要的途徑。本研究簡化了指標體系的構建，實際研究中可對指標體系進行完善。研究說明模糊理論和DUOWA算子的整合可有效地分析和評價銀行服務質量，具有一定的實踐意義。

[1] Karatepe O M,Yavas U,Babakus E.Measuring Service Quality of Banks:Scale Development and Validation[J].Journal of Retailing and Consumer Services 2005,(12).

[2] 金文姬.我國國有商業銀行服務質量研究[J].上海金融,2007,(6).

[3] Zadeh,L.A.Fuzzy Sets[J].Information and Control,1965,(8).

[4] Zadeh,L.A.The Concept of a Linguistic Variable and its Application to Approximate Reasoning-I[J].Information Science,1975,(8).

[5] Yager R R.On Ordered Weighted Averaging Aggregation Operators in Multi-criteria Decision Making[J].IEEE Transactions on Systems,Man and Cybernetics,1988,(18).

[6] Xu.Z.S,Da.Q.L.The Uncertain OWA Operator[J].International Journal of Intelligent Systems，2002，（17）.

[7] Xu.Z.S.Dependent Uncertain Ordered Weighted Aggregation Operators[J].Information Fusion，2008，（9）.