高超聲速飛行器非線性H∞姿態控制設計

王 延，周鳳岐，周 軍，郭建國

（西北工業大學 精確制導與控制研究所，710072 西安，wangyan991926@sina.com）

由式(1)可得:

那么式(2)中的各個函數計算為

閉環非線性系統式(2)，式(9)漸近穩定.

2)當w≠0，得出

高超聲速飛行器非線性H∞姿態控制設計

王 延，周鳳岐，周 軍，郭建國

（西北工業大學 精確制導與控制研究所，710072 西安，wangyan991926@sina.com）

針對高超聲速飛行器傾斜轉彎姿態跟蹤控制問題，將非線性耦合系統的姿態跟蹤控制表述為非線性H∞控制的指令誤差狀態空間實現形式.基于非線性系統γ－耗散性及L2增益設計準則，設計滿足Hamilton-Jacobi-Isaacs不等式的光滑可微儲能函數.在一定假設條件下，利用非線性系統在局部空間內線性伴隨系統的Riccati微分方程，獲得非線性H∞控制問題在鄰近指令誤差狀態空間的局部空間解，來解決非線性耦合系統的H∞控制問題.實驗結果表明，該方案避免了復雜的Hamilton-Jacobi-Isaacs不等式求解過程.

高超聲速飛行器;非線性H∞控制;L2增益;Hamilton-Jacobi-Isaacs不等式

高超聲速飛行器控制問題中穩定性、控制性能以及魯棒性等是其主要關心的問題.目前對高超聲速飛行器魯棒控制研究大部分集中在縱向模態，且大部分都是以忽略模型之間相互耦合影響為前提的［1－3］，而非線性魯棒控制方法普遍是基于動態逆或基于微分幾何精確反饋線性化的控制策略［4－7］.

基于微分幾何的精確反饋線性化過程中要進行大量繁瑣的高階微分運算，動態逆方法對建模誤差非常敏感［8］，需要實現系統精確建模.傾斜轉彎技術能夠適應高超聲速飛行器氣動外形對空氣動力學參數以及大氣條件變化敏感、氣動特性復雜等特性要求，其動力學系統快時變、強耦合.從已有文獻可以看出高超聲速飛行器縱向控制問題已經相當復雜，考慮非線性耦合模型時，控制問題將變得更復雜，這給實際應用帶來較大的難度.

非線性H∞控制作為一種先進的魯棒控制方法，其應用因為繁瑣的 HJI(Hamilton-Jacobi-I-saacs)不等式求解而受限.文獻［9－10］基于L2增益分析，提出了平滑仿射非線性系統H∞控制的完整解決方案.文獻［11－12］將上述方法擴展到含有非光滑摩擦力的動力學模型，并應用于機械控制.本文針對高超聲速飛行器非線性耦合系統傾斜轉彎姿態跟蹤控制問題，建立高超聲速飛行器H∞傾斜轉彎姿態跟蹤模型，為了解決該非線性耦合系統控制問題，放寬文獻［11－12］的應用條件，設計非線性H∞姿態跟蹤控制器.該方案通過求解非線性H∞控制問題在鄰近指令狀態點的局部空間解，避免非線性H∞控制設計中復雜的HJI不等式求解過程，通過仿真驗證了該方法滿足高超聲速飛行器傾斜轉彎姿態跟蹤控制設計要求，具備較好的魯棒性能.

1 高超聲速飛行器姿態跟蹤動力學模型

高超聲速飛行器傾斜轉彎H∞姿態控制設計目的是設計H∞控制器使得飛行器滾轉角γ跟蹤滾轉角指令γc，攻角α跟蹤攻角指令αc，保持側滑角β跟蹤βc=0，且系統內部漸近穩定.因此選取狀態變量為

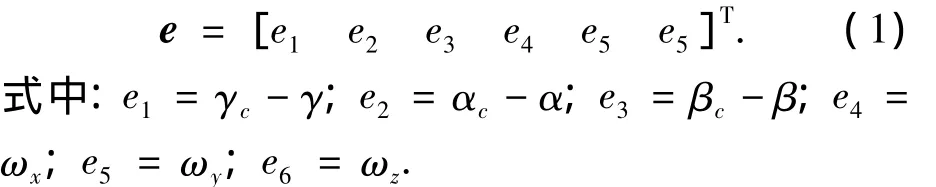
建立高超聲速飛行器傾斜轉彎姿態跟蹤動力學模型為

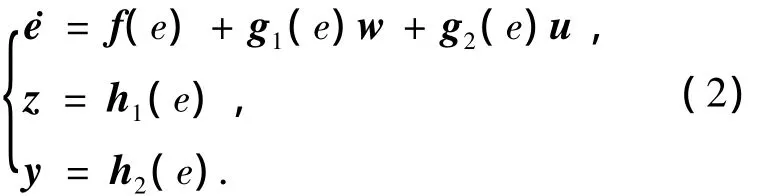
由式(1)可得:

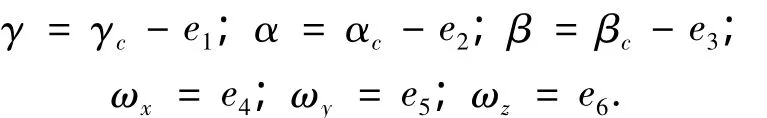
那么式(2)中的各個函數計算為

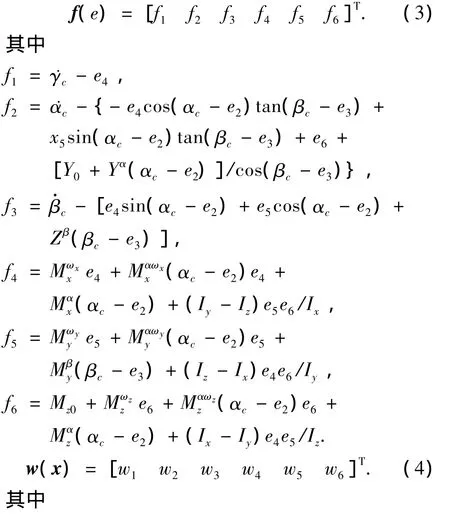
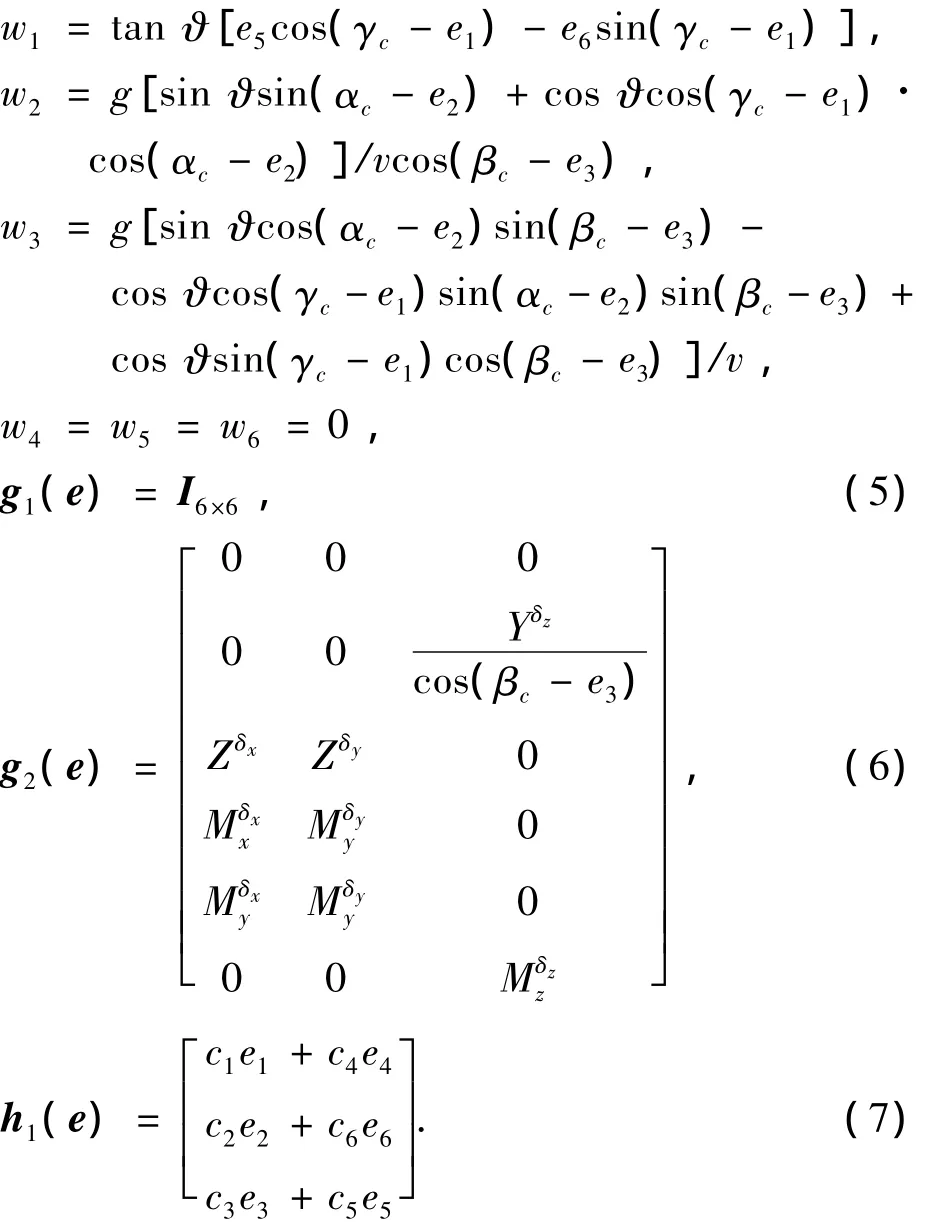
式中c1～c6為常數參量.

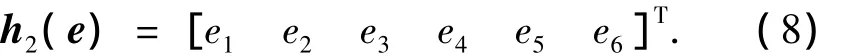
跟蹤動力學模型式(2)沒有作γ、α、β小角度假設，沒有作三通道解耦處理，是一個嚴重非線性耦合系統，其中耦合包含了慣性耦合、氣動耦合及控制量耦合.

2 一種非線性H∞控制方法的全局解

文獻［11－12］中為了解決包含非光滑摩擦力的非線性機械模型H∞控制問題，對被控模型做出了很多的假設限制條件.為了借鑒其控制方案設計思路應用于連續光滑的高超聲速飛行器非線性姿態跟蹤動力學模型，放寬其應用限制條件，對于形如式(2)的光滑非線性耦合系統，做出如下假設為:

假設1 e∈ Rn，u ∈ Rm，w ∈ Rr，z∈ Rl，y∈Rp;

假設 2 f(e)，g1(e)，g2(e)，h1(e)，h2(e)是分段連續函數，且滿足局部Lipschitz條件;

假設3 存在反饋控制u使得式(2)漸近穩定.

那么非線性系統式(2)的H∞控制問題表述為:給定正數λ＞0，設計反饋控制器為

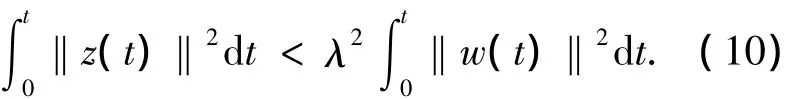
使得對任意給定的t＞0，當初始狀態e0=0，初始內狀態ξ0=0時，表示為即使得閉環非線性耦合系統式(2)，式(9)的L2增益 ＜λ.這樣，如果該系統是零狀態可檢測的(即當z(t)→0時，e(t)→0成立)，根據La Salla定理可知e0=0是該系統的漸近穩定平衡點［14］.

為了解決上述問題，做出下述2個假設:

假設4 存在平滑正定函數V(e)，使得HJI不等式成立.

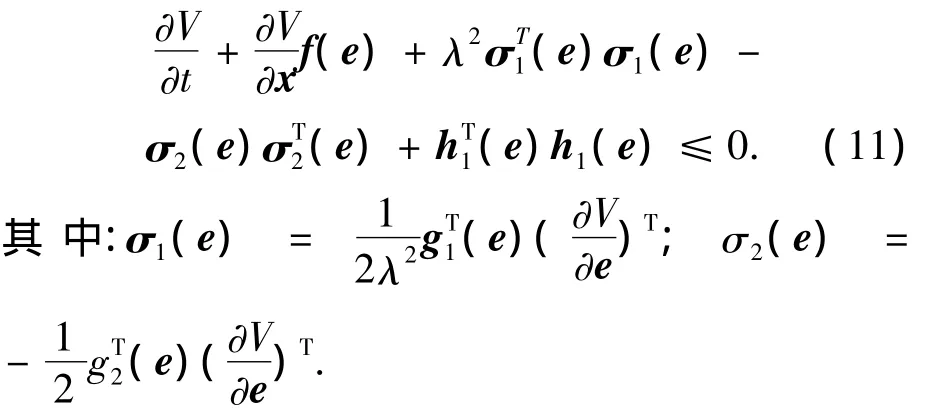
假設5 存在分段連續函數，平滑半正定函數W(e，ξ)且 W(e0，ξ)正定，使得 HJI不等式成立為

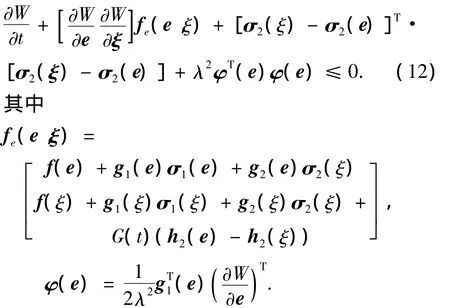
在假設4，5基礎上有下列定理:

定理1 若假設4)，5)對于非線性耦合系統式(2)成立，那么存在反饋控制為

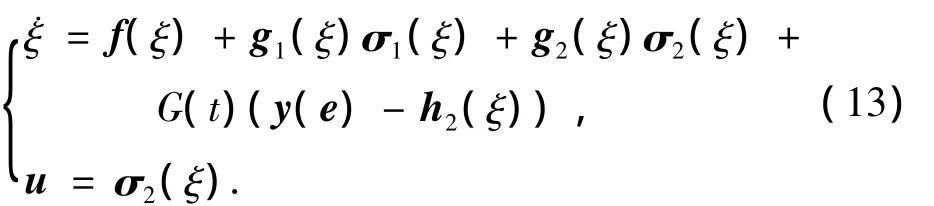
使得非線性耦合系統式(2)全局漸近穩定，閉環系統式(2)，式(9)的L2增益 ＜λ.

證明 首先定義函數為

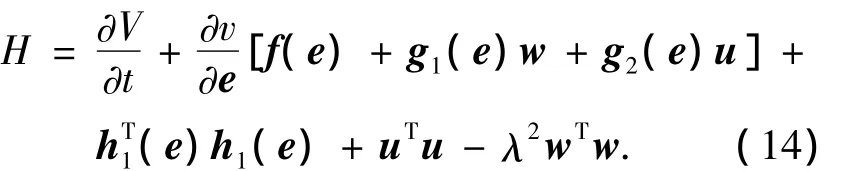
將式(14)分別對w、u求導，得出

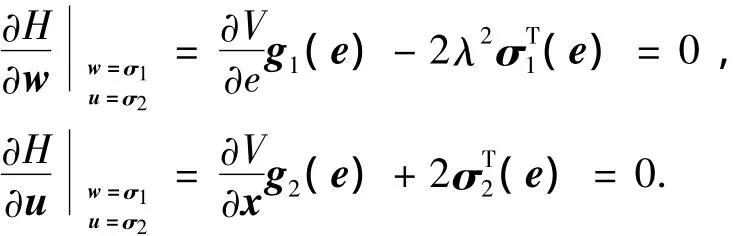
將式(14)用泰勒級數展開為

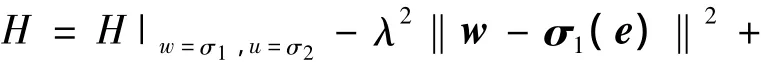
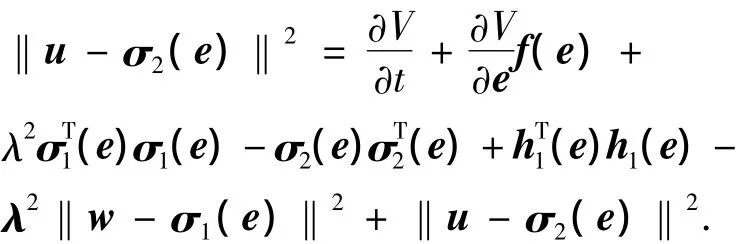
假設4，計算為

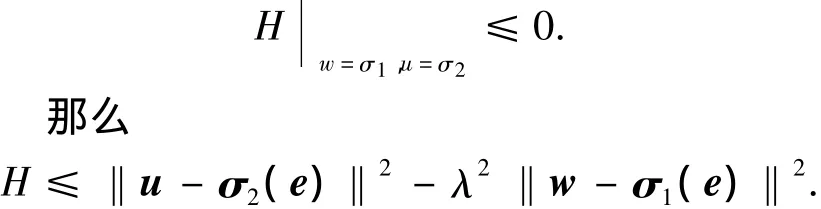
因此得到:

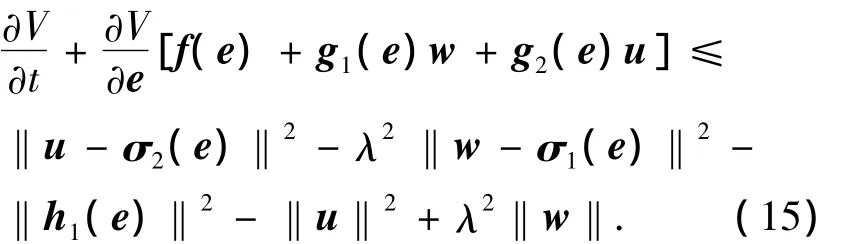
接著，定義函數為

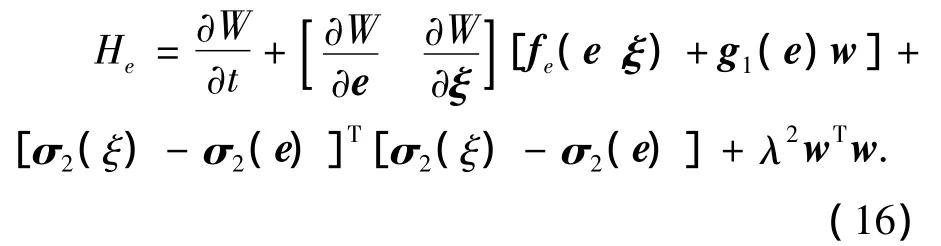
同理可得

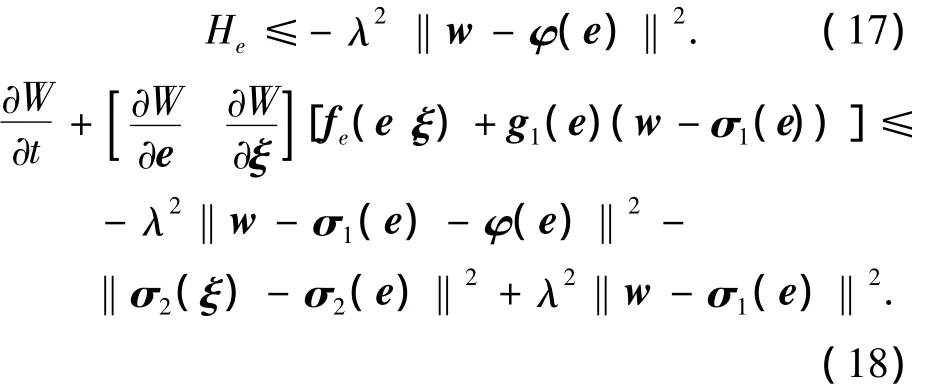
那么構造有界正定函數為

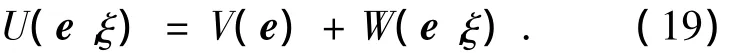
將式(19)對時間t求導為:

1)當w=0，得出

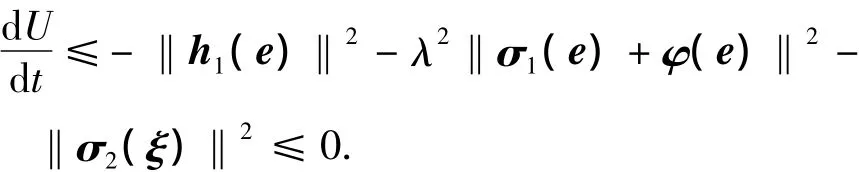
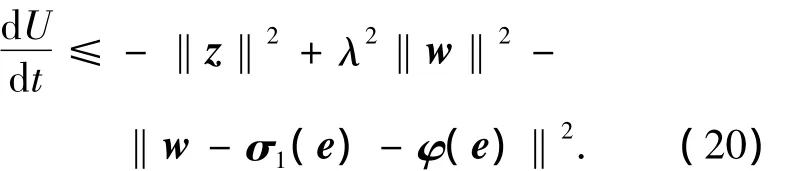
任意給定的t＞ 0，當初始狀態(e0，ξ0)=(0，0)時，對式(20)積分得出

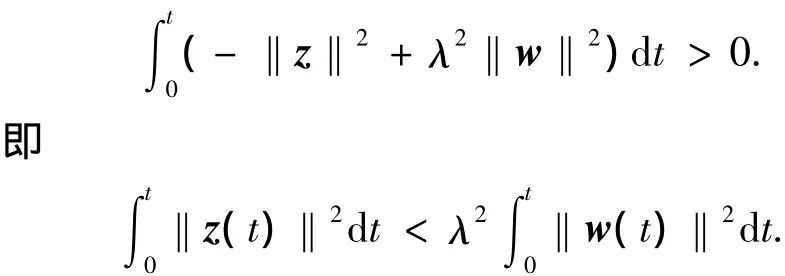
閉環非線性系統式(2)，式(9)漸近穩定.

2)當w≠0，得出

閉環非線性系統式(2)，式(9)的L2增益 ＜λ.

證畢.

因此，式(13)即為上述非線性H∞控制問題的全局解.實際上，在飛行器控制應用中不是必須得到全局解，而只需要在飛行航跡附近的局部空間內使得系統漸近穩定，L2增益 ＜λ即能夠滿足飛行器飛行要求，這樣將大大簡化控制器設計的難度.

3 非線性控制的局部狀態空間解

若非線性系統式(2)同時滿足下述假設:

假設6 對任意給定的t＞0，函數g1(e)，g2(e)，h1(e)，h2(e)在鄰近e0=0的局部狀態空間內關于e二次連續可微，且在某一給定的局部狀態空間內，一階、二階導數分段連續且一致有界.

若滿足假設6，則在鄰近e0=0的局部狀態空間內，存在非線性系統式(2)的線性伴隨系統為

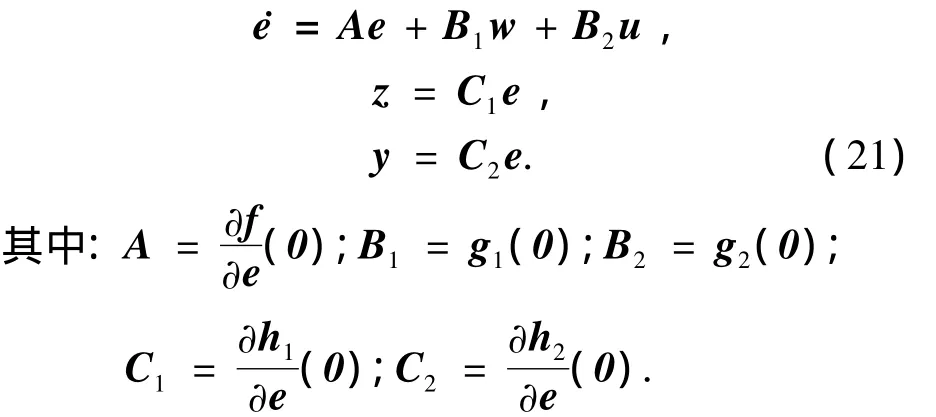
若在鄰近e0=0的局部狀態空間內，線性伴隨系統式(21)滿足可穩定可觀測條件，那么文獻［15］得出了如下結論:

結論1 存在對稱半正定矩陣解P使得指數穩定為

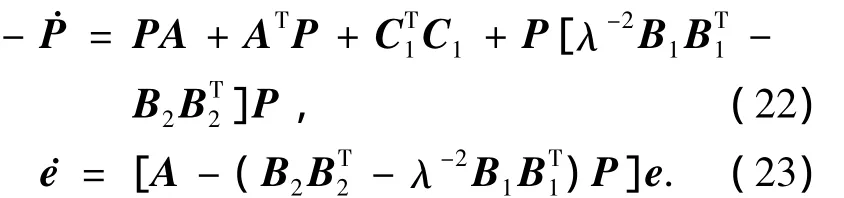
結論2 存在對稱半正定矩陣解P使得指數穩定為

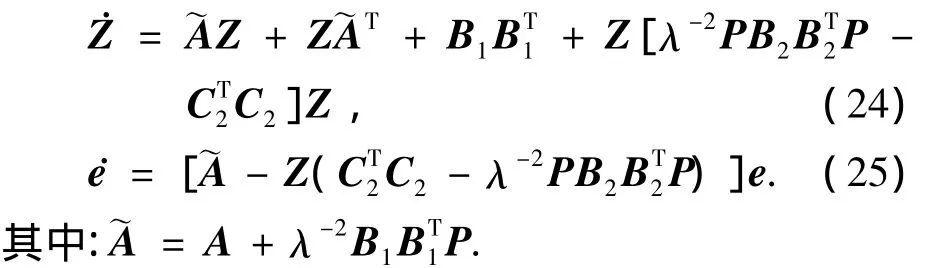
由結論1，2可以得出下列推論:

推論2 存在一個正常數ε0，當ε∈(0，ε0)時，局部伴隨線性系統式(21)的Riccati方程存在唯一的有界對稱正定解(Pε，Zε)為

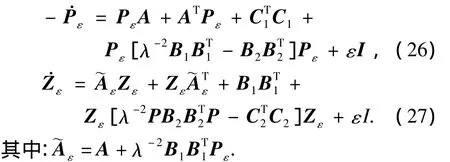
定理3 若滿足推論2，那么給定正數常λ＞0，ε＞0，由式(26)，(27)解得有界對稱正定解(Pε，Zε)，反饋控制為

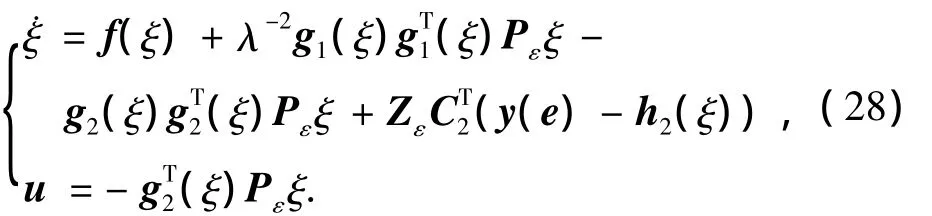
使得閉環非線性系統式(2)，式(28)在鄰近(e，ξ)=(0，0)的局部狀態空間內漸近穩定、L2增益 ＜λ.

證明 由推論2，在(e，ξ)=(0，0)周圍的局部空間，依據假設條件4，5定義如下函數:

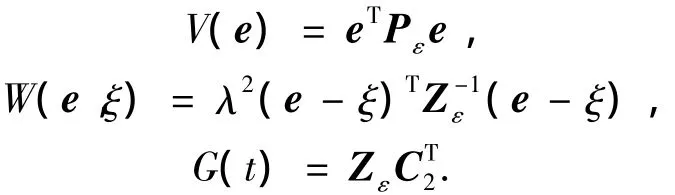
對應HJI不等式式(11)得到:

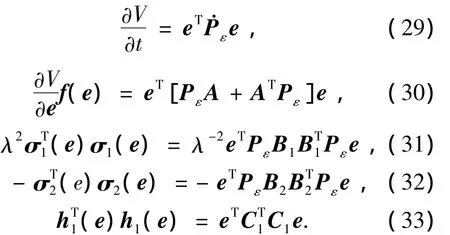
將式(29)～(33)代入式(11)得到:

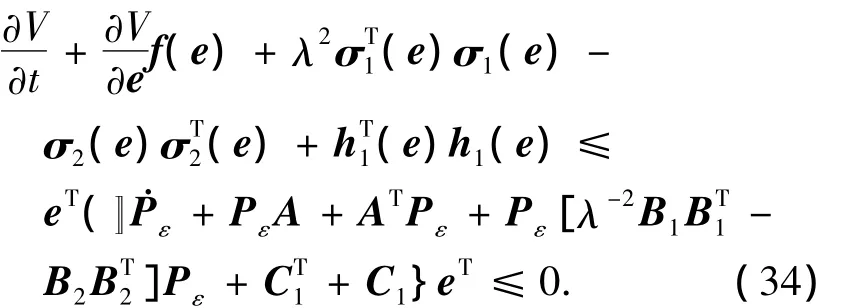
對應不等式HJI式(12)得到:

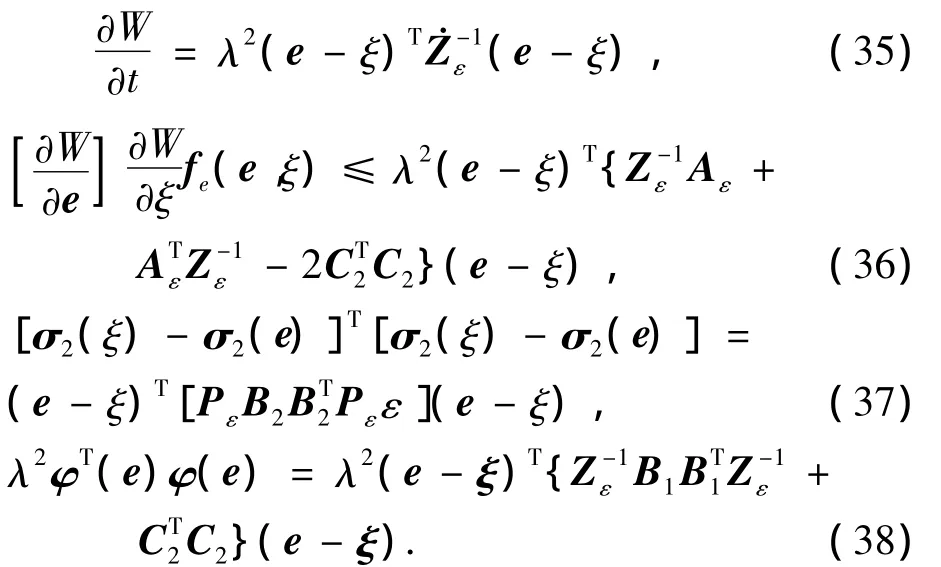
由式(27)得到方程:

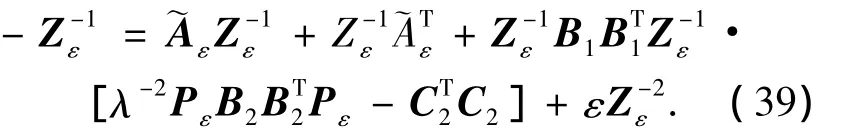
將式(35)～(39)代入式(12)得到:

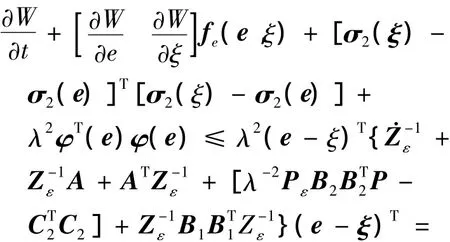
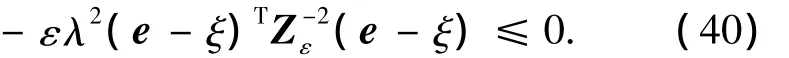
根據定理1，由式(34)，(40)得出反饋控制式(28)是式(2)的非線性H∞控制問題在鄰近(e，ξ)=(0，0)的局部狀態空間內的局部解.

證畢.

實際應用中，根據高超聲速飛行器H∞傾斜轉彎姿態跟蹤控制系統模型式(2)，在飛行航跡附近的狀態空間內，求解鄰近指令狀態點(e，ξ)=(0，0)的局部狀態空間解式(28)，使得閉環非線性系統式(2)，式(28)在上述局部空間內L2增益 ＜λ，系統漸近穩定.

4 仿真結果

選擇仿真條件:飛行高度h=50 km，馬赫數M=20.應用Matlab軟件進行跟蹤10°滾轉角方波指令、10°攻角方波指令和0°側滑角指令控制系統仿真驗證.仿真中，三通道舵偏與實際中3個舵面舵偏的關系為

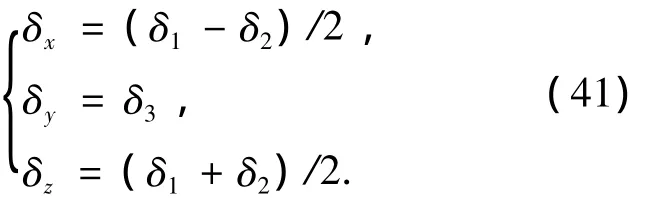
如圖1，當從彈身后方沿機體系X軸向前觀察時，安裝在右翼后緣的右側升降舵記為δ1，安裝在左翼后緣的左側升降舵記為δ2，安裝在垂尾后緣的方向舵記為δ3.左、右升降舵后緣下偏為正偏轉，方向舵后緣右偏為正偏轉.

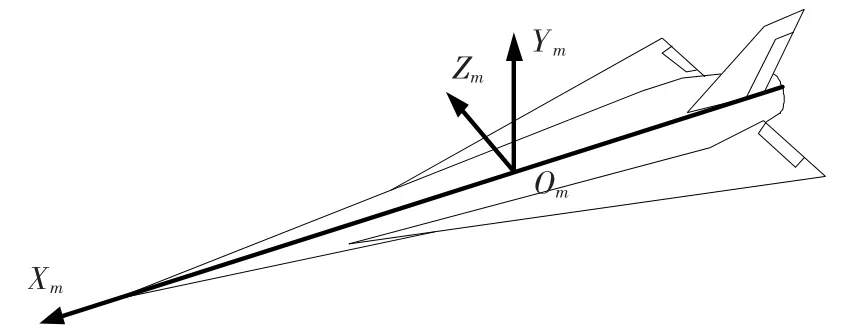
圖1 高超聲速飛行器

仿真中，假設實際舵系統為二階環節，舵系統的輸入指令與實際輸出之間的傳遞函數為

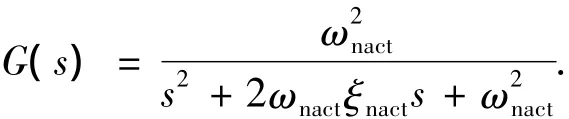
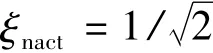
仿真結果如圖2～7所示，設計的控制方法滿足設計要求:控制系統具有良好的指令跟蹤能力，側滑角β趨近于0°，最大誤差 ＜2°;跟蹤攻角α方波指令，穩態誤差 ＜2%;跟蹤滾轉角γ穩態誤差 ＜1%，γ響應有些緩慢，是因為系統實際舵面控制作用耦合，按照式(41)的實際舵面分配，舵效無法同時使2個通道的跟蹤效果達到最優;控制系統具備很好的魯棒性能，當氣動參數攝動±30%時，跟蹤控制效果影響很小.

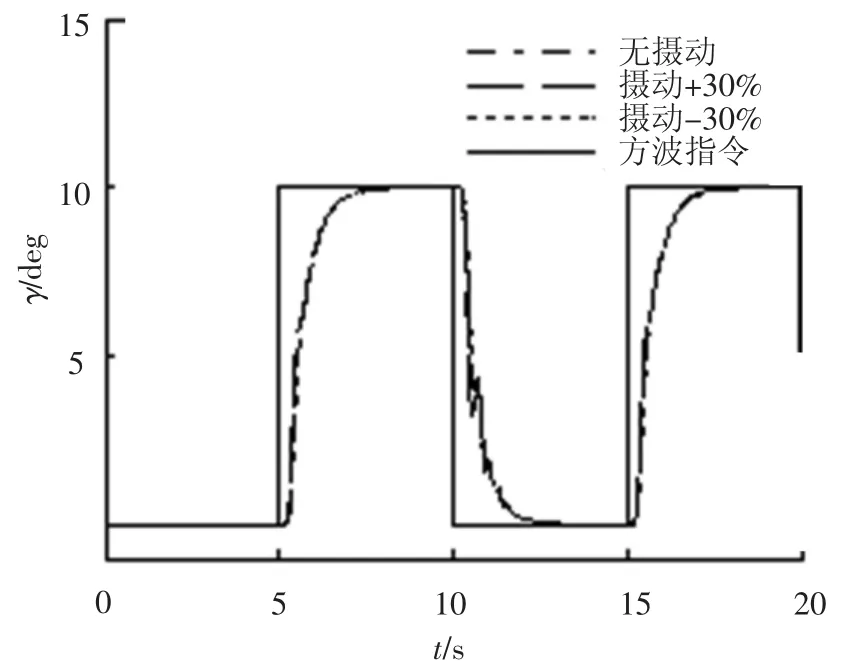
圖2 滾轉角響應

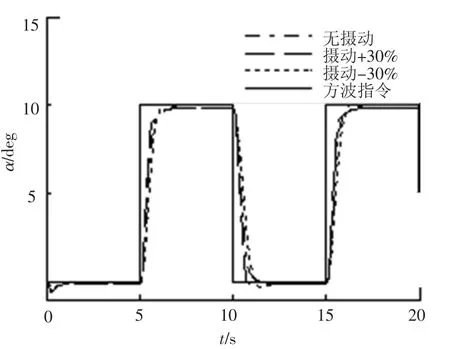
圖3 攻角響應

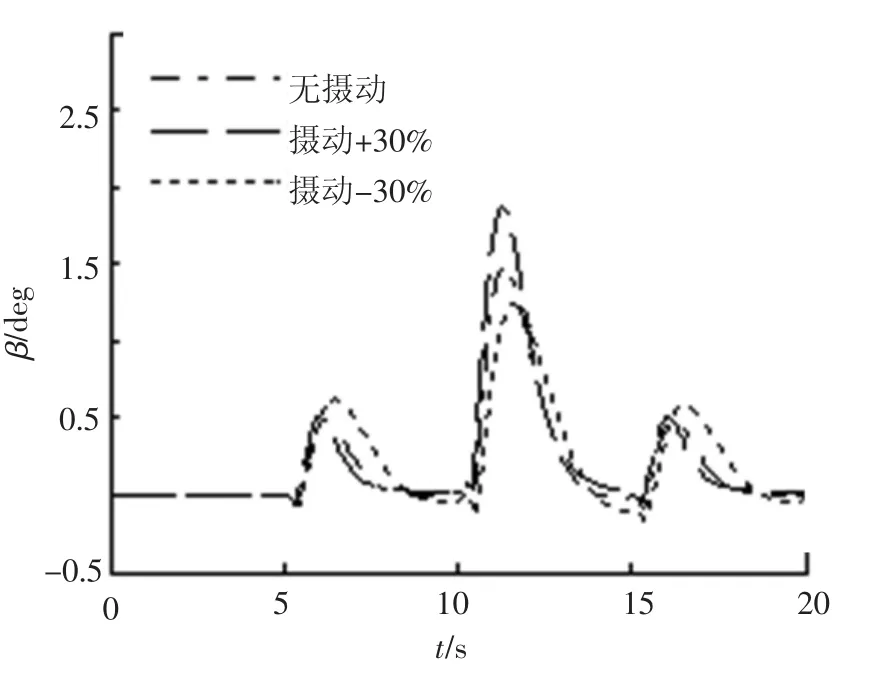
圖4 側滑角響應

實際上，仿真中可實現氣動參數攝動±38%時仍有較好的魯棒性能，當超出這個范圍控制結果將發散.即參數攝動＜±38%，系統處于滿足本文控制策略的局部狀態空間內，參數攝動 ＞±38%，系統就超出了非線性控制器局部狀態空間解的設計范圍.實際工程中該控制策略在多大范圍的局部狀態空間內可行，還與具體被控對象模型有關.

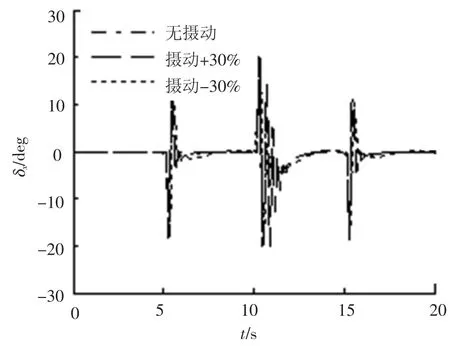
圖5 滾轉通道舵偏

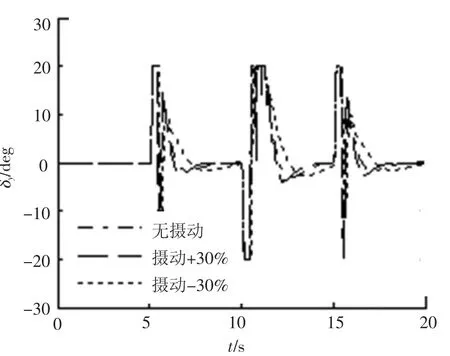
圖6 偏航通道舵偏

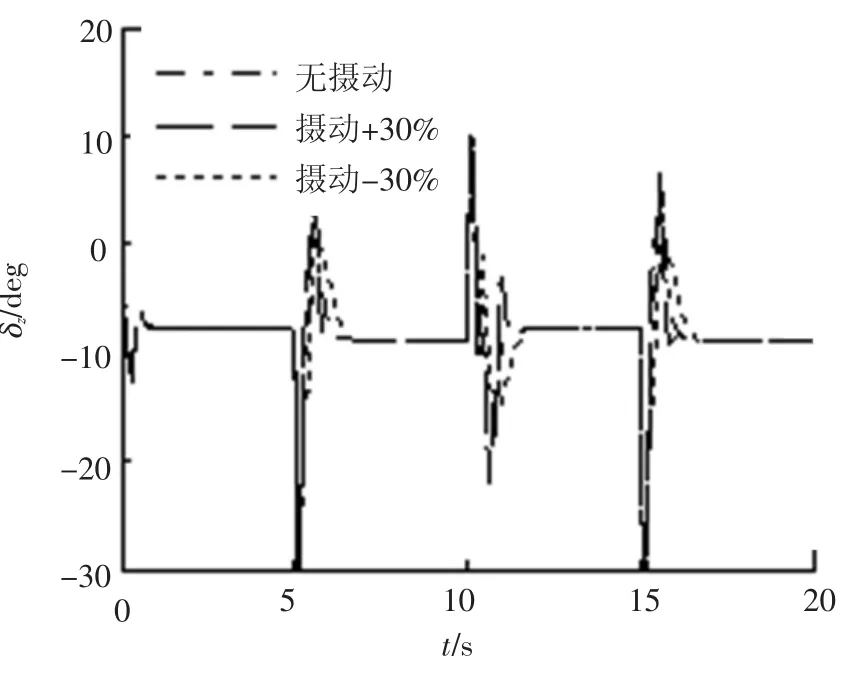
圖7 俯仰通道舵偏

5 結 論

1)針對高超聲速飛行器非線性耦合系統姿態跟蹤控制問題，建立高超聲速飛行器H∞傾斜轉彎姿態跟蹤控制系統模型，設計非線性H∞姿態跟蹤控制器.

2)該方法利用局部空間內伴隨系統的Riccati微分方程，避免了非線性H∞控制問題中復雜繁瑣的HJI不等式解算過程，便于實際應用.仿真驗證了該方法滿足性能設計要求，具備較強的魯棒性能.

［1］GREGORY I M，MCMINN J D，SHAUGHNESSY J D.Hypersonic vehicle control law development using H∞and μ-synthesis［R］.NASA TM －4562，1994.

［2］BUSHCEK H，CALISE A J.Uncertainty modeling and fixed-order controller design for a hypersonic vehicle model［J］.Journal of Guidance，Control，and Dynamics，1997，20(1):42 －48.

［3］LOHSOONTHORN P，JONCKHEERE E，DALZELL S.Eigenstructure vs constrained Hxdesign for hypersonic winged cone ［J］.Journal of Guidance，Control，and Dynamics，2001，24(4):648 －658.

［4］HELLER M，SACHS G.Flight dynamics and robust control of a hypersonic test vehicle with ramjet propulsion［C］//AIAA International Space Planes and Hypersonic Systems and Technologies Conference.Norfolk:AIAA，1998:126－136.

［5］JENNIFER G，JOHN V.Selection of longitudinal desired dynamics for dynamic inversion controlled re-entry vehicles［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.USA:AIAA，2001:1－11.

［6］XU H J，IOANNOU P A，MIRMIRANI M.Adaptive sliding mode control design for a hypersonic flight vehicle［J］.Journal of Guidance，Control and Dynamics，2004，27(5):829－838.

［7］WANG Q，STENGEL R F.Robust nonlinear control of a hypersonic aircraft［J］.Journal of Guidance，Control and Dynamics，2000，23(4):577 －584.

［8］BRINKER J S，WISE K A.Stability and flying qualities robustness of a dynamic inversion aircraft control law［J］.Journal of Guidance，Control and Dynamics，1996，19(6):1270－1277.

［9］ISIDORI A，ASTOLFI A.Disturbance attenuation and H∞－control via measurement feedback in nonlinear systems［J］.IEEE Transactions Automatic Control，1992，37(9):1283－1293.

［10］Van Der SCHAFT A J.L2－gain analysis of nonlinear systems and nonlinear state feedback H∞control［J］.IEEE Transactions on Automatic Control，1992，37(6):770－784.

［11］ORLOV Y，ACHO L，SOLIS V.Nonlinear H∞－control oftime-varying systems［C］//Proceedings of the 38th conference on decision and control.Canada:AIAA，1999:3764－3769.

［12］AGUILAR L T，ORLOV Y，ACHO L.Nonlinear H∞－control of nonsmooth time-varying systems with application to friction mechanical manipulators［J］.Automatica，2003，39(7):1530－1542.

［13］彭冠一.防空導彈制導控制系統設計［M］.北京:宇航出版社，1996:236－240.

［14］梅生偉，申鐵龍，劉康志.現代魯棒控制理論與應用［M］.北京:清華大學出版社，2003:172－182.

［15］RAVI R，NAGPAL K，KHARGONEKAR P.H∞control of linear time-varying systems［C］//Proceedings of the 29th Conformer on Decision and Control.USA:AIAA，1990:1796－1801.

Design of nonlinear H∞controller for hypersonic vehicle system

WANG Yan，ZHOU Feng-qi，ZHOU Jun，GUO Jian-guo

(Institute for Precision Guidance and Control，Northwestern Polytechnical University，710072 Xi'an，China，wangyan991926@sina.com)

For the BTT attitude tracking control problem of hypersonic vehicle，a state-error-space implementation expression of nonlinear H∞attitude tracking control for above nonlinear coupling system is given firstly.Then basing on γ－energy-dissipation and L2gain performance criterion in nonlinear system theory，the smooth differentiable stored-energy function is designed，which subject to the Hamilton-Jacobi-Isaacs inequality.Following some assumptions，a local state-space solution of nonlinear H∞attitude-tracking control problem for nonlinear coupling hypersonic vehicle system is obtained，by using Riccati differential equation of linear following system in local state-space.The local state-space is the neighborhood around the command state error space.Above approach avoids complicated solving process of Hamilton-Jacobi-Isaacs inequality，thus it's a good reference for engineering.

hypersonic vehicle;nonlinear H∞control;L2gain;Hamilton-Jacobi-Isaacs inequality

V44

A

0367－6234(2011)09－0128－06

2011－06－02.

航天科技創新基金資助項目(N11XW0001).

王 延(1979—)，男，博士研究生;

周鳳岐(1935—)，男，教授，博士生導師;

周 軍(1966—)男，教授，博士生導師.

(編輯 張 紅)