BS 5400規(guī)范中大偏心受壓短柱極限承載能力計算

王青太

1 概述

隨著中國土木工程設(shè)計走出國門，進入更加廣闊的國際市場，面對更加激烈的競爭環(huán)境，要求設(shè)計的產(chǎn)品更加安全、經(jīng)濟、合理，同時，也要求設(shè)計人員在熟練運用國內(nèi)規(guī)范的同時，積極了解、學(xué)習(xí)國外規(guī)范。

在斯里蘭卡鐵路的初步設(shè)計中，深入研究了BS 5400-4規(guī)范中，鋼筋混凝土柱極限承載能力的計算方法，并進行了合理的簡化，總結(jié)整理如下。

2 計算原理及假設(shè)

2.1 計算原則和假設(shè)

根據(jù)BS5400-4中5.5.3.2規(guī)定，柱的截面抵抗力計算假定如下:

1)混凝土的壓應(yīng)變與鋼筋的拉、壓應(yīng)變，符合平截面假定;

2)當橋墩截面為矩形和圓形時，混凝土的應(yīng)力值按整個受壓面積上(0.4×fcu)MPa考慮;在所有情況下，截面最外緣混凝土破壞時的極限壓應(yīng)變值應(yīng)取0.003 5;

3)不考慮混凝土的抗拉強度;

4)鋼筋的應(yīng)力值從圖1得出，其中，γm取1.15。

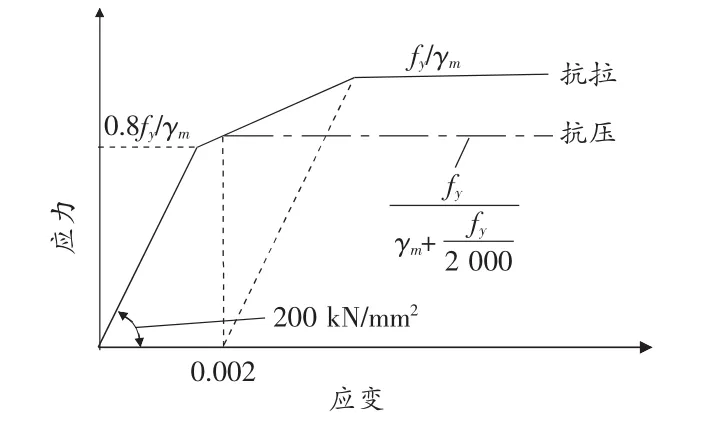
圖1 鋼筋應(yīng)力—應(yīng)變曲線

2.2 計算公式

根據(jù) BS 5400-4∶1990 中 5.5.3.2，5.5.3.3 和 5.5.3.4 條規(guī)定，采用式(1)，式(2)計算截面抵抗力、力矩，步驟如下所述:

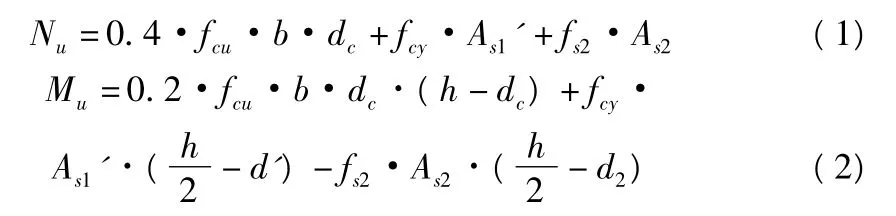
其中，N為由極限荷載組合在檢算截面產(chǎn)生的設(shè)計軸向荷載;M為由極限荷載組合在檢算軸產(chǎn)生的設(shè)計彎矩，包括初始的施工容許誤差;Nu，Mu分別為當dc取合適的假定值時，截面的極限軸向抗力值和極限彎矩抗力值;fcu為混凝土的立方體抗壓強度;b為截面的寬度;dc為截面假定的受壓區(qū)高度，最小值為2d';fcy為受壓較強側(cè)鋼筋的設(shè)計強度值，N/mm2，fcy=fy/(γm+fy/2 000);As1'為受壓較強側(cè)受壓鋼筋的面積;fs2為另一側(cè)的鋼筋應(yīng)力值，拉應(yīng)力取負值;As2為另一側(cè)鋼筋的面積，作用如下:受壓;不起作用;受拉。當荷載合成偏心值增加，此時dc值從h減少到2d'，另一側(cè)鋼筋按順序出現(xiàn)以上三種情況;h為彎曲平面的全截面高度;d'為受壓較強側(cè)截面外緣至鋼筋中心處的距離;d2為另一側(cè)截面外緣至鋼筋中心處的距離。

3 計算公式簡化

3.1 基本假設(shè)

1)鋼筋的拉、壓應(yīng)力極限值都取鋼筋應(yīng)變?yōu)?.002時對應(yīng)的應(yīng)力值。

2)計算Mu時，只計入達到設(shè)計強度鋼筋對抵抗彎矩的貢獻，即只計入L1，L2高度范圍內(nèi)的鋼筋作用(因未達到設(shè)計強度的鋼筋面積很小，可以忽略不計，且檢算結(jié)果偏安全)。

3.2 計算公式和步驟

3.2.1 計算圖示

x—x軸和y—y軸的截面抵抗彎矩值計算原理相同，故以下以x—x軸截面抵抗彎矩計算為例。

由本文2.1節(jié)內(nèi)容，得到x—x軸截面抵抗彎矩值的計算圖示，見圖2。

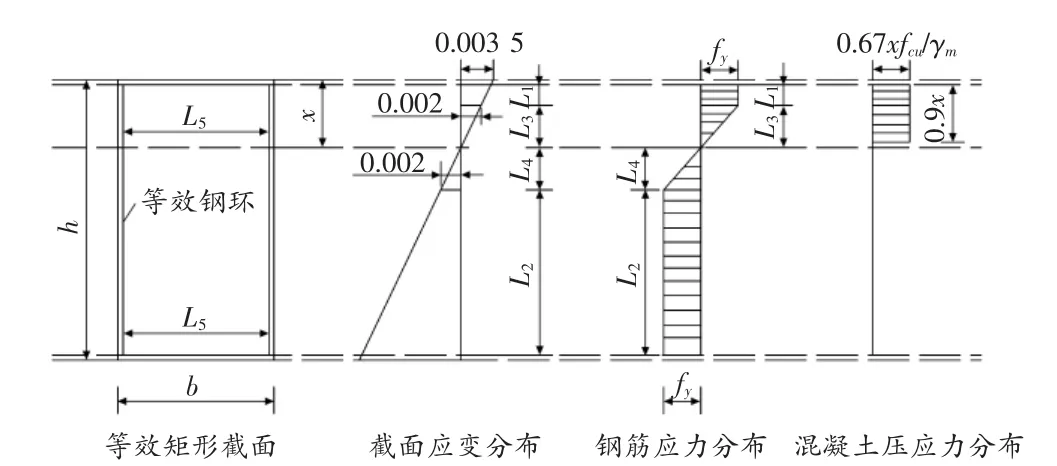
圖2 計算圖示

3.2.2 計算公式整理

1)設(shè)dc≥2d'=2×75 mm=150 mm，此時最外側(cè)受壓鋼筋達到極限應(yīng)變值，即最外側(cè)受壓鋼筋達到設(shè)計強度。

此時:

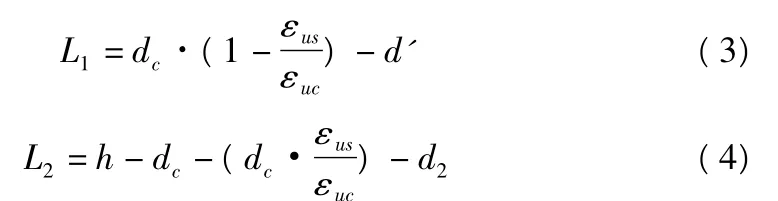
其中，L1，L2分別為達到極限壓應(yīng)變和極限拉應(yīng)變的鋼環(huán)在y軸方向上的高度;dc為截面假定的受壓區(qū)高度，最小值為2d';εus為鋼筋極限應(yīng)變值，本設(shè)計中取0.002;εuc為混凝土極限壓應(yīng)變值，本設(shè)計中取0.003 5;d'為受壓較強側(cè)截面外緣至受壓鋼筋中心處的距離;h為截面高度;d2為另一側(cè)截面外緣至鋼筋中心處的距離。

2)式(1)具體化。

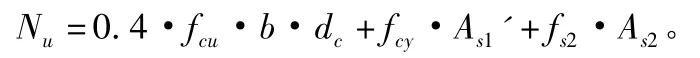
可以具體成:

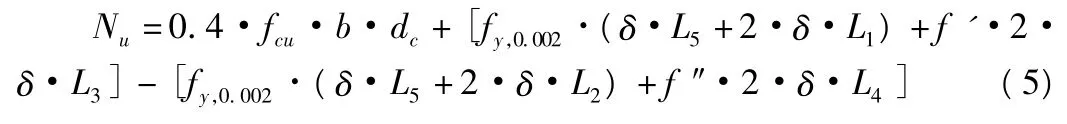
其中，fy，0.002為鋼筋拉、壓強度設(shè)計值2 000);δ為截面配筋等效成鋼環(huán)時的厚度值，δ=［(D/2)2·π］/Δ，D為鋼筋直徑，Δ為鋼筋間距;Nu為截面極限軸向抵抗力;L1為達到受壓強度設(shè)計值鋼環(huán)沿y軸高度;L3為未達到受壓強度設(shè)計值鋼環(huán)沿y軸高度;f'為未達到受壓強度設(shè)計值的鋼筋的平均強度值;f″為未達到受拉強度設(shè)計值的鋼筋的平均強度值;L2為達到受拉強度設(shè)計值鋼環(huán)沿y軸高度;L4為未達到受拉強度設(shè)計值鋼環(huán)沿y軸高度;L5為最外排達到設(shè)計強度的受拉、受壓鋼環(huán)長度。根據(jù)平截面假定，由幾何關(guān)系知:

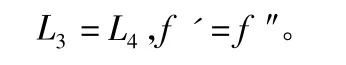
式(5)可以整理為:

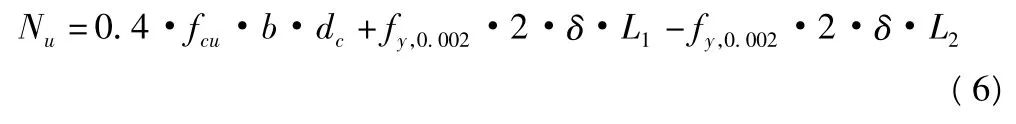
3)式(2)具體化。

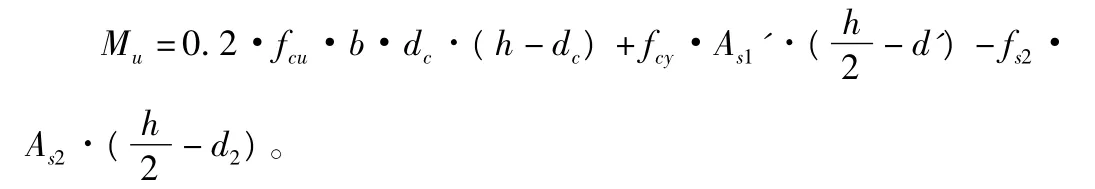
具體成:

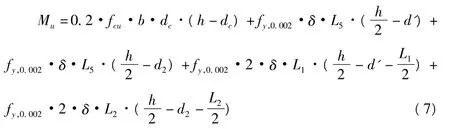
其中，Mu為繞x軸截面極限抵抗力矩。其余參數(shù)定義同上。

3.2.3 計算步驟

大偏心受壓短柱，假定ULS下，軸向荷載設(shè)計值N為截面極限軸向抵抗力 Nu，代入式(6)，同時將式(3)、式(4)也代入式(6)，得到:

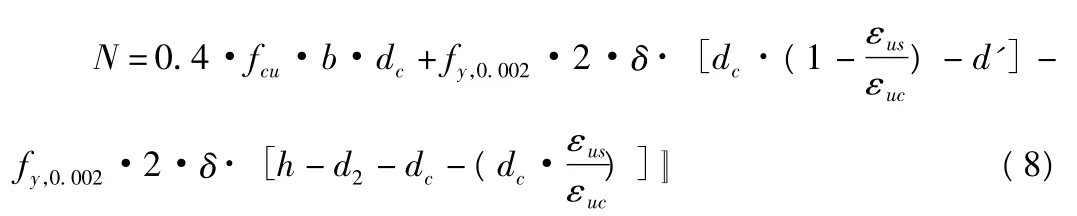
式(8)中，只含有dc一個未知量，故由式(8)可以解得dc，判斷dc滿足下式:

其中，db為當混凝土和受拉鋼筋同時達到極限應(yīng)變值時，截面的受壓區(qū)高度。

將dc代入式(7)，同時將式(3)、式(4)代入式(7)，即可求得截面繞x軸的極限抗彎承載能力。

4 結(jié)語

BS5400-4∶1990規(guī)范中，鋼筋混凝土短柱的極限承載能力，以平截面假定和材料的應(yīng)力、應(yīng)變曲線為基礎(chǔ)，推導(dǎo)出截面的抵抗力，計算方法更加嚴謹、合理，計算結(jié)果較國內(nèi)規(guī)范更加經(jīng)濟。本文提出的簡化方法，在滿足工程精度要求的同時，使計算更加便捷。

［1］ BS5400-4，混凝土橋設(shè)計規(guī)范［S］.

［2］ JTG D62-2004，公路鋼筋混凝土及預(yù)應(yīng)力混凝土橋涵設(shè)計規(guī)范［S］.

［3］ TB 10002.3-2005，鐵路橋涵鋼筋混凝土和預(yù)應(yīng)力混凝土結(jié)構(gòu)設(shè)計規(guī)范［S］.

［4］ 靳 杰，王 濤.鋼筋混凝土異形柱框架地震反應(yīng)譜分析［J］.山西建筑，2010，36(21):62-63.