加筋結構動力特性和動力響應分析

趙望勝 劉 澔 葉建新

在土木工程中，由于基體材料的性能不足，大量使用各種加筋材料來增強和改善結構的力學性能。加筋結構中加筋材料與基本材料作用方式復雜，選擇合理的有限元模型便于模擬加筋構件布置的情況，可以很好的模擬加筋構件與基本材料之間相互作用情況，實現對加筋結構進行動力特性和動力響應分析。

目前，在實際過程中，總伴有不同類型的阻尼力，產生這種阻尼力的因素可歸結為兩個方面:1)外部介質的摩擦阻尼力;2)結構內部變形時的內耗。由于材料結構組成復雜，導致阻尼力性質很復雜，這類振動力學計算尚沒有很好的解決。

1 動力學的精細積分算法

一般而言，確定線性系統的動力方程可寫為:

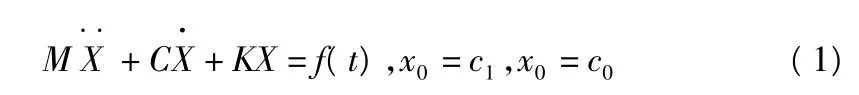
其中，M，C，K分別為質量矩陣、阻尼矩陣、剛度矩陣;f(t)代表激勵，假設自由度為n，將式(1)寫成狀態方程:

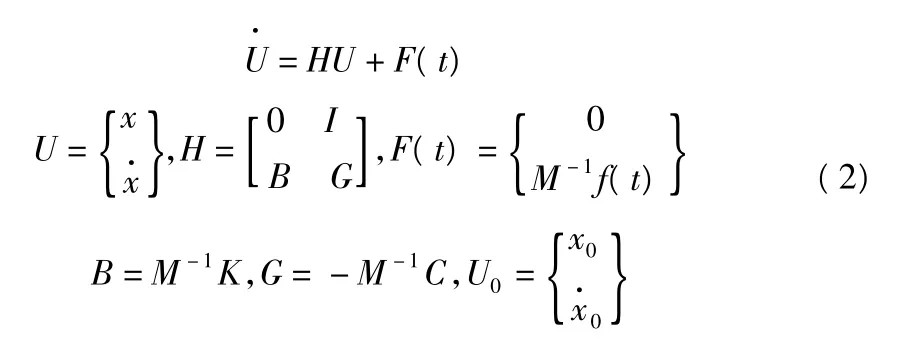
對式(2)，它的解可寫成如下形式:

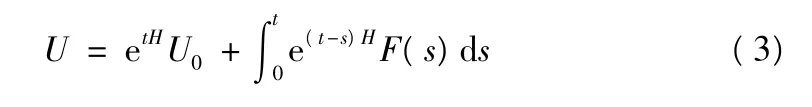
對式(3)進行數值離散，并假設時間步長Δt=tk+1－tk，則第k+1步時的響應公式可寫為:

對式(4)可作如下變形:

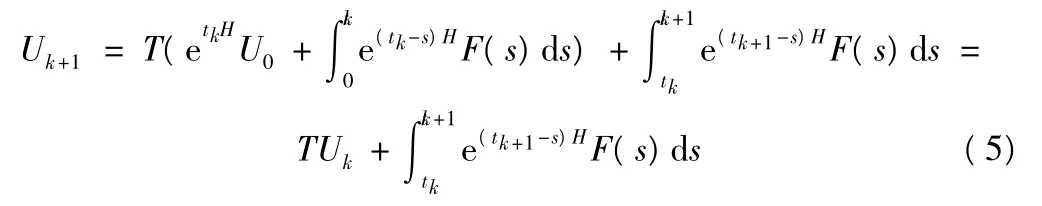
在式(5)中，T=exp(ΔtH)，它可用數值方法精細計算而得。為使式(5)也能直接進行數值計算，可用數值積分方法將其式中的第二項算出。在這里，選用格式較為簡單同時精度又較高的辛普森積分法，也即:

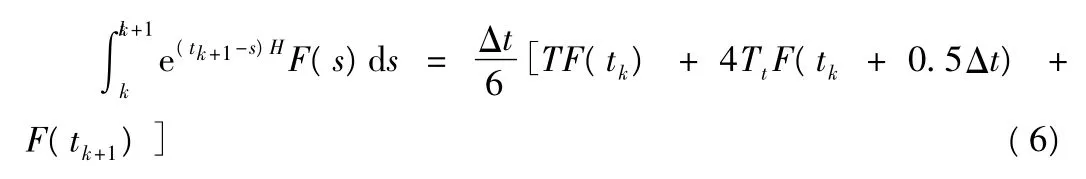
其中，Tt=exp m(0.5ΔtH)，所以式(4)可變為:

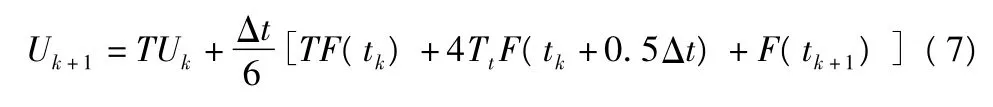
式(7)即是計算系統響應的迭代公式。

2 模型

加筋構件靜力學算例問題，如圖1所示。混凝土一端固定，另一端一節點處受有集中力作用，混凝土的彈性模量E=2.0e10、密度 ρ=2 400 kg/m3、泊松比 v=0.3，鋼筋彈性模量 E=2.0e11、密度 ρ=9 000 kg/m3、截面面積 0.08 m2、泊松比 v=0.3。集中力F=1.0e4。

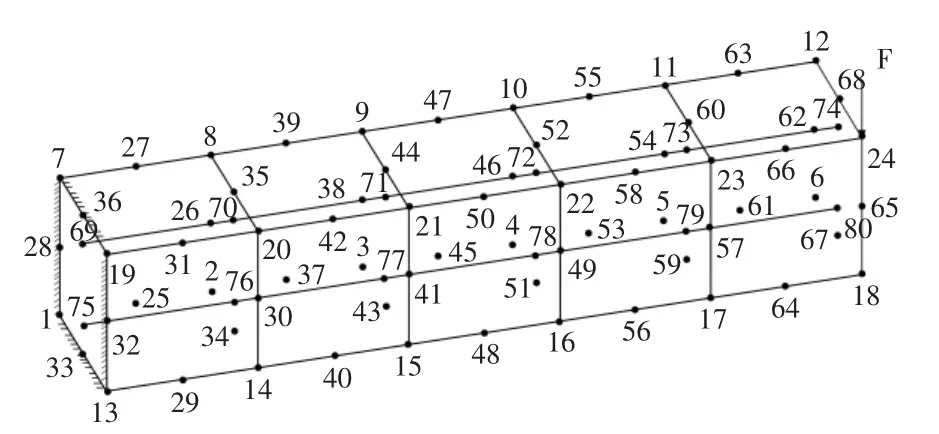
圖1 加筋結構示意圖

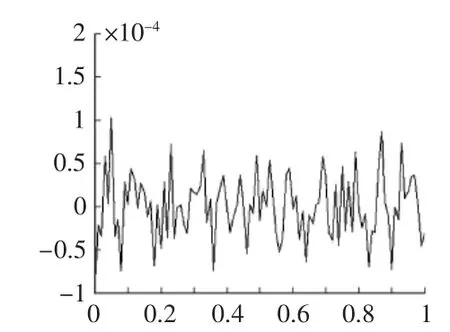
圖2 加筋結構的無阻尼自由振動

圖3 無鋼筋結構的無阻尼自由振動

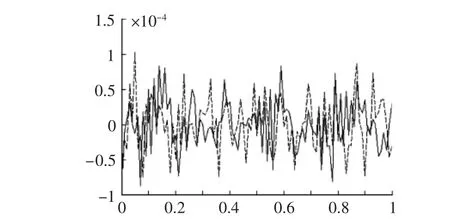
圖4 無鋼筋結構和加筋結構的無阻尼自由振動比較

3 模型結果和分析

針對如圖1所示的模型，在這里為了表示結構自由振動模型的準確性，選取加筋結構在荷載作用下的位移作為結構自由振動的初始位移，而速度假設為0。可以理解為加筋結構受到靜力荷載后突然釋放的自由振動，這種情況更適合實際情況。阻尼C=1.0e－2M+2.0e－4K(M，K分別為結構的質量陣和剛度陣)。圖2，圖3是加筋結構和不考慮加筋結構在初始位移激勵下的無阻尼自由振動，圖4是考慮鋼筋和不考慮鋼筋結構的無阻尼自由振動對比示意圖。

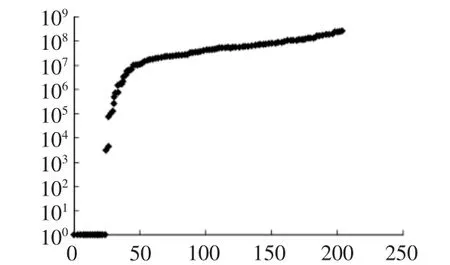
圖5 加筋結構的固有頻率對數曲線

從圖4可以看出，加了鋼筋后，結構抵抗振動的能力變強，也說明鋼筋對整個結構的固有頻率有增大的作用。為了更直觀的說明這個問題，在求解出結構(加筋和非加筋結構)的質量陣和剛度陣之后，就可以得到其固有頻率，如圖5，圖6所示。

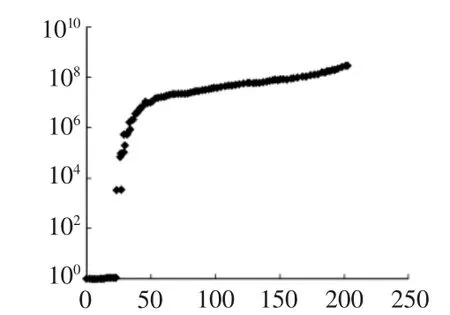
圖6 無筋結構的固有頻率對數曲線

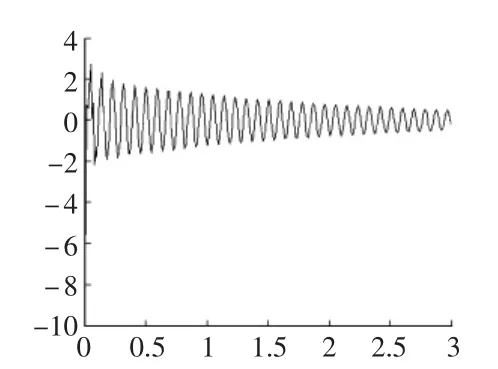
圖7 加筋結構有阻尼自由振動

表1是得到結構的剛度陣和質量陣后，求解出來的結構的部分自振頻率。從表1的頻率對比可以看出，加筋結構的自振頻率比無筋結構的自振頻率要大，這也說明了鋼筋對結構有剛度貢獻，從而提高了結構的自振頻率。圖7是有阻尼的自由振動結構的示意圖，從圖7可以看出位移有規律的逐漸衰減，這正是所期待的結果。

表1 加筋和無筋結構的固有頻率比較

4 結語

狀態方程直接積分法不僅用于求解在線性激勵、簡諧激勵作用下系統的動力響應，還可以求解在一般荷載作用下系統的動力響應;不僅可以用于求解線性系統的動力響應，還可以用于求解非線性系統動力的響應計算，且精度高，速度快。

為有阻尼和無阻尼結構振動計算分析帶來極大的方便，進而解決加筋結構中加筋的布置，從而為提高結構穩定性分析研究做出了理論計算分析價值。算例就是很好表明了加筋后結構的穩定性明顯提高。

［1］ 尹曉芷，劉彥昌.鋼筋混凝土梁動力特性檢測研究［J］.山西建筑，2009，35(4):104-105.

［2］ 夏樟華，宗周紅.預應力對混凝土梁動力特性的影響分析［J］.振動與沖擊，2007，26(7):129-134.

［3］ 杜金龍，郭少華.鋼筋混凝土損傷梁動力特性的有限元分析［J］.石家莊鐵道學院，2007，20(3):18-23.

［4］ 鐘萬勰.暫態歷程的精細計算方法［J］.計算結構力學及其應用，1995，12(1):1-6.

［5］ 鐘萬勰.矩陣黎卡提方程的精細積分［J］.計算結構力學及其應用，1994，11(2):113-119.

［6］ 張森文，曹開彬.計算結構動力響應的狀態方程直接積分法［J］.計算力學學報，2000(2):95-96.

［7］ 張相庭.結構振動力學［M］.上海:同濟大學出版社，2005.