基于加權Voronoi圖的連續型物流節點布局優化＊

王 偉 封學軍

（河海大學港口海岸與近海工程學院水運規劃與物流工程研究所1） 南京 210098）（長沙理工大學公路工程省部共建教育部重點實驗室2） 長沙 410004）

國內外學者采用調查法、雷利法則、引力模型、需求勢能理論、系統建模等方法［1－4］研究了物流節點的合理服務范圍劃分；相關學者還基于物流節點服務范圍的分析，基于重心法、鮑姆爾－沃爾夫法、雙層規劃、混合整數規劃、圖論等方法構建了物流節點布局優化模型［5－6］，系統地研究了物流節點數量、選址、規模的綜合優化問題.現有的研究雖能概要性確定物流節點服務范圍，但未能綜合反映物流節點對服務區域的吸引，難以滿足動態性、系統性的要求，且只是粗略的劃分，在一定程度上限制了物流節點布局優化研究的深度和準確性.

本文采用引力模型來確定物流節點對區域空間的吸引力，引入加權Voronoi圖來實現物流系統空間服務范圍的動態精確劃分，在此基礎上，構建連續型物流節點布局優化模型，提出模型的高效求解算法.

1 加權Voronoi圖

加權Voronoi圖［7］的定義如下：

設P＝（P1，P2，…，Pn），3≤n＜∞為二維歐氏空間上的一個控制點集；λi（i＝1，2，…，n）是給定的n個正實數，則

將平面分成n部分，由V（pi，λi）（i＝1，2，…，n）確定的對平面的分割稱為點上加權的Voronoi圖，稱λi為pi的權重.

加權Voronoi圖的生成可采用離散生成算法，此方法無需復雜的計算，容易實現［8］.同時，考慮到物流節點存在多層級情況，假設物流節點的競爭只存在于同級別的節點之間，對于多層級物流節點服務范圍的劃分可以轉化為多個單層級內物流節點服務范圍劃分問題，通過多次離散生成法來實現.

2 物流節點服務范圍劃分的引力模型

物流節點服務范圍的劃分要考慮到內外部環境中的諸多因素，物流節點服務范圍的確定與節點的層級、功能、規模、服務對象緊密關聯，提出如下假設：物流節點的功能是一致的；只考慮同層級物流節點之間的競爭；物流節點對服務區域的吸引力也存在“規模效應”和“遞遠遞減”的現象.構建物流節點的吸引力模型來解決物流節點服務范圍劃分的問題［9］，設有n個物流節點（同一層級），s個需求點（可將區域物流系統服務區域劃分為若干個小區），則物流節點i對需求點j的吸引力為

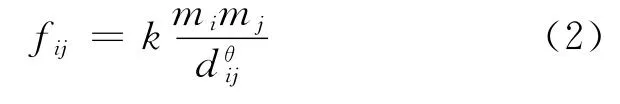
式中：mi為物流節點或其所在區域的“質量”，即物流節點的競爭力，這里選擇物流節點規模、區位交通條件、技術作業水平及效率和所在區域的經濟總量4個因素來確定物流節點綜合競爭力

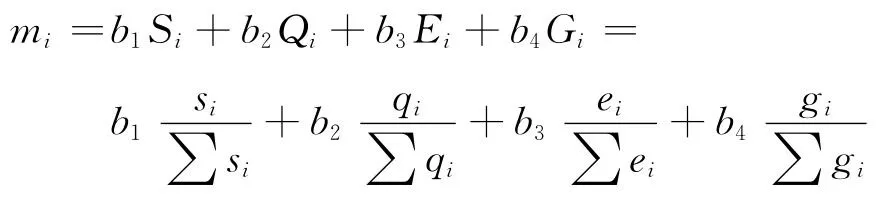
其中：si，qi，ei，gi分別為物流節點i的規模、區位交通條件、技術作業水平、所在區域的經濟總量，Si，Qi，Ei，Gi分別為其歸一化后的值；b1，b2，b3，b4為權重系數，b1＋b2＋b3＋b4＝1，可采用 AHP法確定.

dij為需求點j到物流節點i的廣義費用，這里取運輸里程、運輸時間和運輸費用3個主要因子構建路權函數，dij＝a1Lij＋a2Tij＋a3Fij＝其中：lij，tij，fij分別為需求點j到物流節點i的運輸里程、運輸時間、運輸費用，Lij，Tij，Fij分別為其歸一化后的值；a1，a2，a3為權重系數，a1＋a2＋a3＝1，可采用AHP法確定；

k為引力系數；θ為引力衰減指數，以［1，2］為宜.

同時，考慮到物流節點作業能力限制等條件，對物流節點服務范圍劃分可采用多次劃分的方式，即當物流節點i飽和度大于1時，對需求點j到物流節點 的廣義費用進行動態調整，進行動態劃分.

3 物流節點布局優化

物流節點布局優化問題可描述為：在規劃目標年負荷分布已知的情況下，以最小的投資和年物流運行費用為目標函數，確定物流節點的數量、位置、容量以及物流節點的服務范圍.優化流程如下：首先，根據目標年物流總需求、已有物流節點供給容量以及候選物流節點規模與類型確定新建物流節點的最大個數nmax和最小個數nmin，利用整數規劃技術得到新建物流節點的容量組合；在確定了新建節點的個數及容量組合之后，采用最大空心圓策略產生新建節點初始選址方案，基于加權Voronoi圖和最大空心圓策略，結合模擬退火算法實現新建物流節點的選址、規模與布局的方案優化［10－12］.

3.1 確定初始方案

基于Voronoi圖最大空心圓定位策略的基礎上，給出根據已有節點及負荷分布情況產生新建物流節點初始選址的方法，具體步驟如下.

步驟1以已有物流節點位置為頂點，產生Voronoi圖.

步驟2求出各節點對應的最大空心圓.

步驟3根據規劃目標年負荷分布情況及負荷密度來確定閾值常數ε（ε是2個新建節點間距離的最小允許值），比較節點qi與qj（i≠j；j＝1，2，…，r）間的距離dij；若dij≤ε，再比較qi與qj對應的最大空心圓的半徑，將半徑較小的最大空心圓所對應的節點刪去.

步驟4若新建節點個數為n，取半徑較大的前n個最大空心圓所對應的節點作為新建節點初始選址.

3.2 方案分析及評價

評價函數如下

式中：Ccost為年物流成本；Si為第i個新規劃物流節點的規模；f（Si）為第i個新規劃物流節點的投資；u（Si）為第i個新規劃物流節點的年運行費用；wij為第i個物流節點至第j個需求點之間的單位運輸費用；lij為第i個物流節點至第j個需求點之間的運輸距離；pij為第i個物流節點與第j個需求點間的需求量；r0為貼現率；α為折算系數.

3.3 方案優化步驟

結合加權Voronoi圖與進化策略算法進行多物流節點選址與規模優化的具體步驟如下.

步驟1以已有節點選址和新建節點初始選址為頂點構造加權Voronoi圖，初始權重取1.

步驟2在新建物流節點對應的V曲邊形中，基于模擬退火算法以總物流費用最小為準則對新建節點選址及其規模進行優化.算法步驟如下.

（1）初始化.

（2）生成初始方案S，步驟如下.

①采用Voronoi規則確定各物流節點的位置.

②根據Voronoi規則劃分的物流節點服務范圍需求點的總需求作為節點的規模.

③反復進行②直到各物流節點前后兩次迭代生成的規模相差不大時終止，輸出初始方案.

（3）對k＝1，2，…，L做第（4）至第（7）步.

（4）生成一個新的解S′，步驟如下.

①任去掉一個規劃節點，對其位置重新按照Voronoi圖的原則選擇最佳位置采用Voronoi規則確定物流節點的位置.

②根據Voronoi規則劃分的物流節點服務范圍需求點的總需求作為節點的規模.

③反復進行②直到各物流節點前后兩次迭代生成的規模相差不大時終止，得到新的解S′.

（5）計算增量Δt＝C（S′）－C（S）.

（6）若Δt＜0則接受S′作為新的當前解，否則以概率exp（－Δt／T）接受S′作為新的當前解.

（7）若滿足終止條件則輸出當前解作為最優解，結束程序.終止條件取為連續若干個新解都沒有被接受時或迭代次數達到預計次數時終止算法.

（8）T逐漸減少，且T趨于0，然后轉第（2）步.

對于物流節點需求超過物流節點供給能力限制時采用懲罰函數法進行處理，對于在可行范圍之外的方案進行懲罰.

步驟3再以優化得到的新建節點站址和已有節點站址構造加權Voronoi圖，并計算各物流節點的需求量和負載強度.

步驟4如果新建節點選址變動距離和小于閾值，則結束迭代.

步驟5否則，返回步驟2.

4 實證分析

以區域物流節點布局優化為例進行實證分析，假設規劃區域為640×360的矩形，規劃區域內的每個方格作為一個物流需求點，假設其物流需求量是均勻分布的，各物流節點與需求點間的廣義費用采用物流節點與各網格需求點間的歐式距離來表示。設已有物流節點為10個，其位置見表1，各節點規模服從［100，200］的均勻分布，由計算機隨機生成，規劃節點為40個。通過在Delphi和SQL Server2000平臺下編寫了多級物流節點布局優化系統，在實驗過程中，根據調查情況調整系統參數。

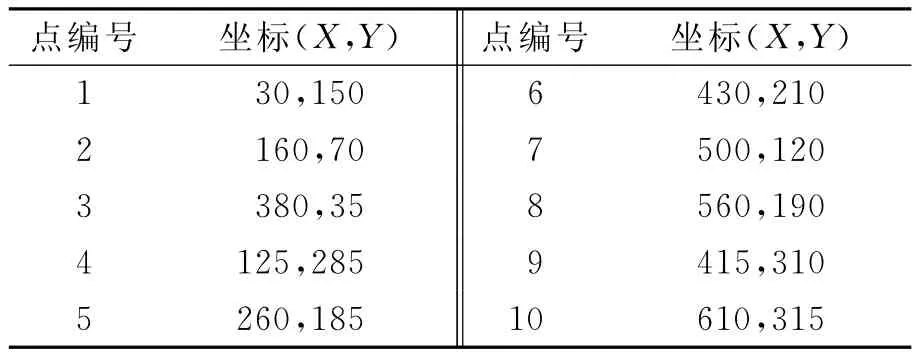
表1 已有物流節點地理位置

1）假設規劃物流節點的規模保持在100，不考慮規劃節點規模優化，重力模型參數θ分別取1和2，現有節點的服務區域劃分結果如圖1所示，生成如圖2所示的初始方案，其目標函數值為126 4762（θ取1）和179 575.5（θ取2）；優化參數為溫度T＝100；Markov鏈長度取50，迭代次數為30次，溫度衰減系數0.95，優化運行過程見圖3.當20次迭代后趨于最優解，其目標函數值為1271 155（θ取1）和179 908.7（θ取2），最終解見圖4.

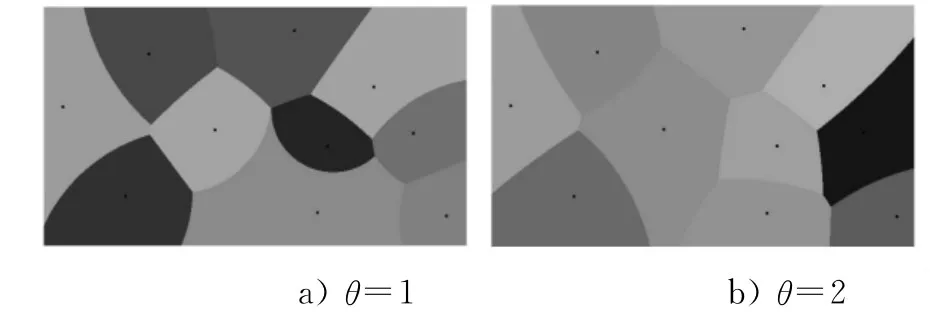
圖1 已有物流節點服務區域劃分結果

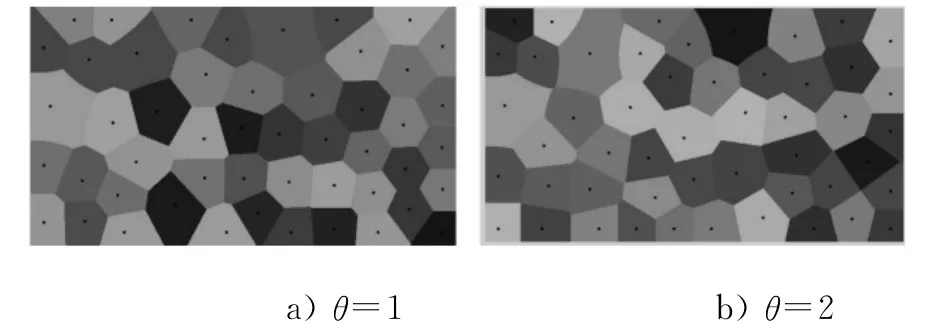
圖2 初始方案物流節點服務區域劃分結果

2）考慮規劃節點規模的優化，重力模型參數θ分別取1和2，則生成如圖5所示的初始方案，其目標函數值為224 488.2（θ＝1）和227 459.3（θ＝2）；優化參數為溫度T＝100；Markov鏈長度取50，迭代次數為30次，溫度衰減系數0.95，優化運行過程見圖6.當θ＝1時，4次迭代后趨于最優解，其目標函數值為266 022.3；當θ＝2時，12次迭代后趨于最優解，其目標函數值為261 239.7.

圖3 規模保持不變情況下的優化過程圖

圖4 規模保持不變情況下迭代20次以后的優化方案

圖5 加入規模優化后的初始方案物流節點服務區域劃分結果

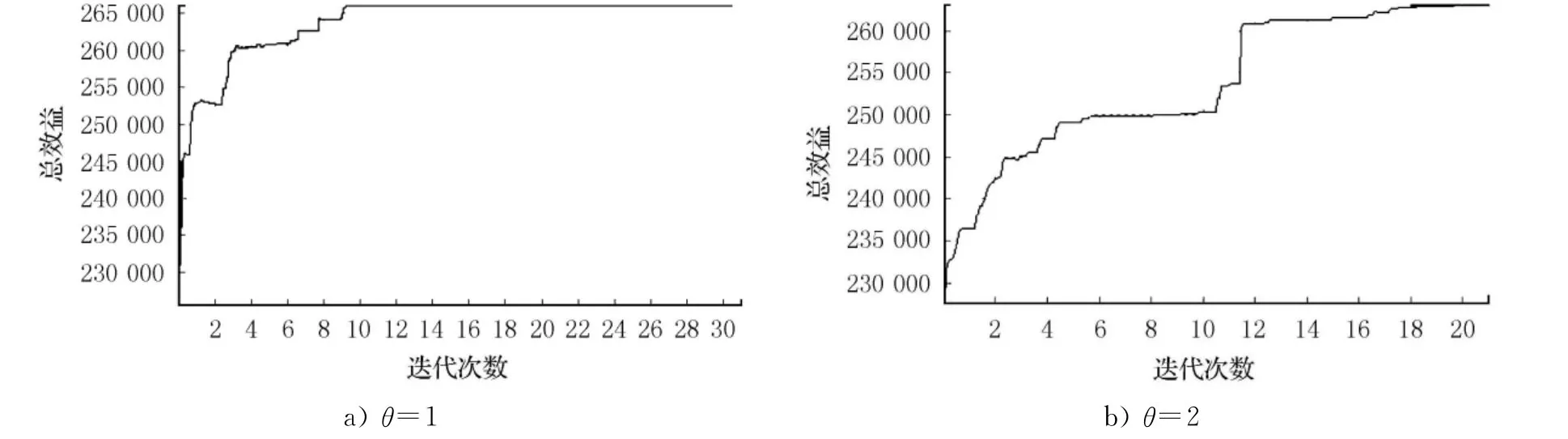
圖6 加入規模優化后的優化過程圖

通過上述優化實例可以看出：

1）與已有的定量劃分方法相比，將GIS技術中的加權Voronoi圖和引力模型相結合，可以實現由多個物流節點構成的區域物流系統動態服務范圍的精確劃分，可以通過多層區域物流體系反映不同等級物流節點服務范圍的層次關系，對于區域物流系統空間服務范圍的劃分，可以基于不同物流節點的功能或者貨種的競爭力、廣義費用等因子，對其進行動態劃分，此方法可用于任意復雜區域物流系統的動態服務范圍劃分，具有較強的實際價值.

2）當不考慮規模優化時，物流節點布局方案中節點布局較為均勻，層次性不明顯；當考慮規模因素時，物流節點布局優化方案中的物流節點呈不均勻布置，物流節點的層次性較為明顯.通過重力模型參數θ的取值不同，可以看出當θ取［1，2］時，θ的值越大，表明物流節點規模對其服務范圍和布局優化的影響越大.通過不同參數條件下SA優化過程對比表明，Markov鏈越長，解質越好但計算時間越長；較小的溫度衰減系數r可以明顯加速算法的進程，但增加了算法陷入局部最優解的可能性.

3）在區域物流節點布局規劃中，考慮到物流需求不是均勻分布的，可以對需求點對應的方格定義一個需求屬性值來表達對應需求點的物流需求量，同時，考慮到物流節點的輻射范圍受到節點到需求點廣義費用的影響，在實際應用中可以在GIS系統中表達區域物流網絡，分析各需求點到物流節點的實際運輸距離、運輸時間以及物流費用來綜合表達各物流節點的引力模型，將更具有實際意義和應用價值.

5 結束語

對物流節點空間服務進行合理劃分能促進物流節點及其服務范圍內相關產業的和諧發展并帶動區域經濟的發展.基于GIS技術中的加權Voronoi圖實現物流節點動態服務范圍的劃分，將加權Voronoi圖與引力模型相結合，充分地考慮了影響物流節點服務范圍的眾多因素，實現了物流節點服務范圍的精確劃分；在此基礎上，構建連續型物流節點協調布局優化模型，結合最大空心圓定位策略和模擬退火算法提出模型的高效求解算法，對解決連續型物流節點資源優化配置是一種嘗試.從算例可以看出，本方法效率高，結果合理，特別是對于區域物流系統，該方法具有其特殊的優勢.

［1］湯宇卿.城市流通空間研究［M］.北京：高等教育出版社，2002.

［2］邱慧芳，郝生躍.基于引力模型的配送中心服務范圍研究［J］.物流技術，2010（2）：82－84.

［3］任冠星，王 轉.需求勢能理論在多級物流網絡預選點中的應用［J］.物流技術，2005（12）：34－36.

［4］張得志，謝如鶴，李雙艷.物流園區布局優化模型及其求解算法研究［J］.武漢理工大學學報：交通科學與工程版，2008，（6）：1 048－1 051.

［5］楊 勇.國內物流中心選址研究方法綜述［J］.物流技術，2008（1）：34－36，43.

［6］黎青松，袁慶達，杜 文.一個結合庫存策略的物流選址模型［J］.西南交通大學學報，2000，35（3）：315－318.

［7］梁 婷.區域物流中心分工布局規劃［D］.長沙：中南大學交通運輸工程學院，2007.

［8］秦 進，史 峰，繆立新，等.考慮隨機需求和庫存決策的多商品物流網絡設計的優化模型與算法［J］.系統工程理論與實踐，2009，29（4）：176－183.

［9］Kobayashi K，Sugihara K.Crystal voronoi diagram and its applications［J］.Future Generation Computer Systems，2002，18（5）：681－692.

［10］趙志輝，李 平，黃曉芹.加權Voronoi圖的離散生成［J］.計算機應用與軟件，2007，24（1）：12－16.

［11］丁鵬飛，王遠飛.基于Relly法則與加權Voronoi圖的連鎖超市商圈分析［J］.上海商學院學報，2005，6（4）：135－139.

［12］葛少云，李 慧，劉 洪.基于加權Voronoi圖的變電站優化規劃［J］.電力系統自動化，2007，31（3）：29－34.