一種基于STL模型的5軸高速加工刀軌優化策略

孫全平， 陳前亮

（淮陰工學院數字化制造技術實驗室，江蘇 淮安 223003）

在過去的幾十年里，CAD/CAM已成為在較短的時間內制造高品質零件的最有力工具。大多數的 CAD/CAM 系統嵌入了支持多種文件格式的數據轉換模塊，以更好地用于航空航天、汽車以及模具領域零部件的設計和制造。三角化（STL）網格格式在近似表達三維曲面上具有很大的優勢。然而，零件越復雜其尺寸精度越高，用于描述的三角片尺寸就越小，大量的微尺寸三角片導致生成的直線段加工刀軌多且短，這不僅影響刀具運轉的穩定性，同時其頻繁的加減速也大幅提高零件的切削時間。因此，對微直線段加工刀軌的數量簡化及其光順性優化就顯得非常重要[1-2]。

相對于3軸加工編程策略，5軸加工的具有加工精度高、周期短、復雜型面更容易的優勢。因此，國內外有不少學者致力于這方面的研究：Langeron and Duc等介紹了一種新的基于B樣條插補用于 5軸加工刀軌計算的后處理格式[3]；Sencer and Altintas提出了一種用于5軸曲面加工的B樣條數控加工刀軌規劃算法[4]；Wang and Liu開發了支持5軸曲線插補功能的控制器[5]。上述學者都是從樣條的光順性角度，研究多軸數控加工，這對于提高切削速度、實現機床的平穩性均有很大幫助，但有點不足的是他們未考慮到基于STL模型規劃的繁多微直線段加工刀軌的簡化，此外，也未考慮到多軸數控加工刀軸矢量的優化。為此，作者提出了多軸數控加工刀軌刀位點簡化算法和刀軸矢量優化算法，給出了支持樣條插補的加工刀軌后處理方法，以適應HEIDENHAIN高速加工數控系統，以最大程度地提高加工效率和表面質量。

1 5軸高速加工刀軌優化

1.1 樣條插補概述

20世紀80年代之后，幾乎所有的CAD/CAM系統都嵌有樣條（Bézier, B-spline和NURBS）的建模功能。為了使數控機床更易于接受和執行從CAD/CAM系統中生成的樣條代碼文件，一些著名的數控系統都嵌入了樣條插補處理器像FANUC 0i的G06.2, SEIMENS 840D的G642以及HEIDENHAIN的SPL。這些插值處理器通常適合樣條建模，若是基于STL建模（見圖1），其后處理過程就相對復雜。首先，在CAM中轉換加工刀軌成 APT代碼，其次，運用直線插補后處理器處理APT代碼為G代碼，接著依靠樣條轉換器轉換G代碼為樣條代碼，最終適應上述數控系統的識讀要求。比較具有相同數量刀位點的G代碼，基于STL模型生成的樣條代碼的數據量明顯增大。

以圖2為例，如果刀具位于OPQRS點，基于直線插補的G代碼可表示如下。

圖1 STL模型

圖2 兩種類型刀軌

由G代碼再轉換成NURBS格式代碼可表示如下。

從此例可看出，樣條插補的代碼量明顯多于直線插補的G代碼量，因此簡化刀位點以提高加工效率就顯得尤為重要，譬如圖2中的 R點，采用樣條插補就可以忽略。

1.2 刀位點簡化

正如圖1所示，如果基于STL模型的三角片都非常小，那么基于這些三角片生成的加工刀軌直線段就很短。為克服繁多微直線段刀軌的缺點，本文把繁多的微直線段刀軌通過加工刀位點簡化算法合并成較長的直線段刀軌（見圖3）。

圖3 微直線段刀軌組合成較長直線段刀軌

其簡化算法的詳細過程敘述如下。

Step 1 從tool-path list中獲取第i行加工刀軌(i=0,2,…, M-1)。

Step 2 計算相鄰兩條直線加工刀軌(tpi, tpi+1)的夾角α 的余弦，如公式（1）所示

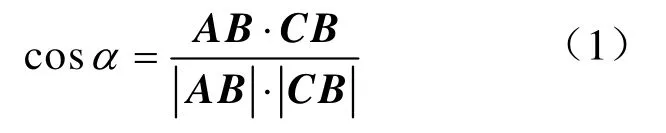
Step 3 如果cosα ≤U，則把相鄰的這兩條直線加工刀軌合并為一條加工刀軌，并把它存入combined- tool-path list。如果cosα >U且相鄰的這兩條加工刀軌是該行起始兩條加工刀軌，就直接將其存入combined-tool-path list，否則，把其后一條加工刀軌存入combined-tool-path list。根據零件的加工精度要求，這里U可取從-0.98到-1之間的某個值。

Step 4 令 i +1 =i，如果 i＜M，返回 Step 2。

Step 5 清空tool-path list，并把combinedtool-path list的數據轉存到tool-path list中，然后清空combined-tool-path list，繼續執行Step1至Step4。

Step 6 運行Step 5三次，結束。

1.3 刀軸矢量優化

通常來說，若一張曲面P(u, v)能用曲線C(u)沿直線 vL(u)掃掠而成，則稱此曲面為直紋面，見公式（2）

式（2）中，u, v：參數變量[6]。

2)第一次空中三角測量，使用POS數據平差(有時這一步驟要反復進行)，主要完成相機校驗和像片模型連接相對定向工作。

如果加工軌跡是直紋面（如圖4），那么刀具的工作平穩性會好，從而其加工的表面質量就高。

圖4 直紋面

刀軸矢量樣條優化，其步驟如下所述。

Step 1 假定原刀軸矢量N(xN, yN, zN)為STL模型上某三角平面片的法向矢量，加工該三角平面片的刀位點為 A(xA, yA, zA)。

Step 2 優化原刀軸矢量N，取原刀軸矢量與Z坐標方向的夾角(θ/2i, i=1,2,…, n)的平分線為臨時刀軸矢量Tj，如圖5所示，它的直角坐標(xTj,yTj, zTj)按公式（3）計算，然后把這些刀軸矢量順序添加到子sub-optimized-orientation list中，接著計算每相鄰刀軸矢量的平均值作為臨時最終的刀軸矢量并添加到 semi-final-orientation list中。

圖5 刀軸矢量的確定

Step 3 對臨時最終的刀軸矢量作干涉檢查，以口腔修復體的三維實體作為毛坯體，刀具的三維實體作為刀具體，進行兩實體的布爾求交運算，如果交集為空，則進入Step 4；否則跳轉Step 5。

Step 4 刀軸矢量進一步優化，清空 suboptimized-orientation list，把 Step 2中的 semifinal-orientation list中的值添加到這個 suboptimized-orientation list中，if i

Step 5 確定最終的刀軸矢量，把 suboptimized-orientation list中的值作為最終的刀軸矢量并添加到final-orientation list中。

Step 6 加工軌跡直紋面擬合，按文獻[6]提出的方法，分別對final-orientation list中的刀位點、矢端點作樣條曲線插值，接著以兩樣條曲線上對應的型值點相連重新生成刀軸矢量，存入axis-orientation list。

1.4 基于優化刀軌的樣條插補計算

為適應 HEIDENHAIN數控系統的樣條插補運算，本文采用三次多項式函數計算 SPL-插補代碼，其插補計算的數學模型為

這里，X、Y、Z、A 和 C：SPL-插補的起始點；X (t)、Y (t)、Z (t)、A (t) 和 Z (t)：SPL-插補的末端點；變量t從0到1變化，t的增量取決于進給率和樣條長度；K3X、K2X、K1X,…K3C、K2C和 K1C：5軸加工刀軌的樣條參數；K3X、K2X和K1X可用公式（4）表示[7]。

圖6表示的是運用SPL-插補方法生成的刀軌樣式。

圖6 5軸聯動樣條刀軌樣式

2 插補精度分析與應用舉例

2.1 精度分析

為證明樣條插補策略用于高速加工的優勢，這里以輪廓加工為例，假定這個圓直徑為20mm，設定用直線離散圓的弦差分別為 2, 1.5, 1, 0.5,0.3, 0.1, 0.05, 0.01, 0.008和0.005（單位：mm），根據這些設定的弦差用直線段逼近這個圓，接著以逼近的直線段的端點作為型值點用樣條曲線插值這個圓，生成的折線與樣條曲線如圖7所示。然后根據所給定弦差計算 SPL-插補策略的圓擬合誤差。兩種插補誤差隨插補點的密化的變化趨勢如圖8所示。

由公式（4）可知，樣條曲線的數量大約是直線段的1/3。從圖8可以看出由樣條插補產生的插值誤差同比直線逼近誤差要小，且有直線逼近誤差越大，相對來說樣條插值精度要高。

這些表明，采用樣條插補生成加工刀軌，不僅加工精度和表面質量較高，而且與直線插補相比，刀具高速運行的穩定性會更好。

圖7 圓的擬合曲線

圖8 兩種插補策略的誤差比較

2.2 應用舉例

為進一步說明樣條插補加工的優越性，基于磨牙冠STL模型，生成了線性插補加工刀軌與樣條插補加工刀軌，進行了加工仿真。結果表明，在磨牙冠的內外表面區域，三角片面的光順性好、三角片的尺寸普遍小（＜0.1mm），兩加工刀軌的一致性好；而在其內外表面的分界處，三角片面的光順性差、三角片的個別尺寸較大（＞0.2mm），兩刀軌明顯不一致，從原始造型的廓形來看，線性插補生成的加工刀軌誤差較大、用于實際加工時刀具易產生顫振。圖9是磨牙冠基于10mm3的毛坯先后采用兩種加工刀軌進行仿真加工的結果。

圖9 仿真加工結果比較

3 結 論

針對三角化網格模型生成加工刀軌多而短的特點以及制作口腔修復體具有精度高、質量好的要求，提出了一種5軸聯動高速加工刀軌優化策略，該策略基于樣條插補，實現了加工刀軌的刀位點的簡化和刀軸矢量的光滑優化，完成了繁多的G代碼向簡捷的樣條代碼轉換。通過理論計算和仿真加工表明，該策略是正確的合理的，不僅可縮短切削時間，而且能避免加工顫振帶來的麻點等表面缺陷。

[1]Su-Jin Kim, Min-Yang Yang. A CL surface deformation approach for constant scallop height tool path generation from triangular mesh [J]. Int J Adv Manuf Technol, 2006, 28: 314-320.

[2]Cheol-Soo Lee, Thu-Thuy Phan, Dong-Soo Kim. 2D curve offset algorithm for pockets with islands using a vertex offset [J]. International Journal of Precision Engineering and Manufacturing, 2009, 10(2): 9-37.

[3]Jean Marie Langerona, Emmanuel Ducb, Claire Lartigue,et al. A new format for 5-axis tool path computation,using Bspline curves [J]. Computer-Aided Design,2004, 36: 1219-1229.

[4]Sencer B, Altintas Y, Croft E. Feed optimization for five-axis CNC machine tools with drive constraints [J].International Journal of Machine Tools & Manufacture,2008, 48: 733-745.

[5]Wang Yongzhang, Liu Yuan, Han Zhenyu. Integration of a 5-axis spline interpolation controller in an open CNC system [J]. Chinese Journal of Aeronautics, 2009,22: 218-224.

[6]施法中. 計算機輔助幾何設計與非均勻有理B樣條[M].北京: 北京航空航天大學出版社, 1994. 452-464.

[7]同濟大學數學系編. 工程數學線性代數[M]. 北京:高等教育出版社, 2007. 21-24.