關于kβ 空間的相關研究

于正文

(山東建筑大學 理學院，山東 濟南 250101)

0 引言

Nagata－空間，k-半分層空間，σ-空間和半分層空間是一類非常重重要的廣義度量空間，作為它們的自然推廣，人們分別引入了wN-空間，kβ-空間，wσ-空間和β-空間，它們在廣義度量空間之間的關系和度量化定理中起著重要作用，但是它們之間的關系并不明確。眾所周知，Nagata-空間?k-半分層空間?σ-空間?半分層空間，且上述關系沒有一個是可逆的。文章探討了wN-空間，kβ-空間，wσ-空間和β-空間之間的關系，并得到類似的結果。

1 定義

定義1［1］空間(X，τ)稱為wN-空間，如果存在映射g:N × X →τ 滿足下列條件:

(1)x ∈g(n，x)，x ∈X，n ∈N;

(2)如果對每個n ∈N，g(n，p)∩g(n，xn)≠?，則{xn}有聚點。

映射g 稱為X 的wN-函數。

定義2［2］空間(X，τ)稱為kβ-空間，如果存在映射g:N × X →τ 滿足下列條件:

(1)x ∈g(n，x)，g(n +1，x)?g(n，x)，x ∈X，n ∈N;

(2)如果對每個n ∈N，K ∩g(n，xn)≠?，這里K 是緊子集，則{xn}有聚點。

映射g 稱為X 的kβ-函數。

定義3［3］空間(X，τ)稱為wσ-空間，如果存在g:N × X →τ 映射使得對每個n ∈N，p ∈g(n，yn)，yn∈g(n，xn)，則{xn}有聚點。

映射g 稱為X 的wσ-函數。

定義4［1］空間(X，τ)稱為β-空間，如果存在映射g:N ×X →τ 使得對每個n ∈N，p ∈g(n，xn)，則{xn}有聚點。

映射g 稱為X 的β-函數。

定義5［4］空間(X，τ)稱為弱子序列式的(weakly subsequential)，如果X 的每個有聚點的序列都有子序列具有緊閉包。

2 主要定理

定理1 每個wN-空間是kβ-空間。

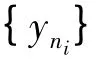
定理2 每個弱子序列式kβ-空間是wσ-空間。

定理3 每個wσ-空間是β-空間。

證明:由wσ-空間和β-空間的定義易驗證定理成立。

3 例子

例1 存在一個kβ-空間不是wN-空間。

設X 是對所有的n ∈N，由［0，∞)粘合1/n 和n 得到的空間，則X 不是wN-空間(見文［5］)。如文［2］所證，X 是k-半分層空間，因此，X 是kβ-空間。

例2 存在一個wσ-空間不是kβ-空間。

空間S 的定義如下:S 的點集是復平面上滿足如下條件的點構成。(1)Imz=0 且Rez 是無理數;或(2)Imz ＞0 且Imz 和Rez 均為有理數。對S 的每個1型的點z(即Imz=0)，定義B(n，z)={x ∈S:Imx＜| Re(x－z)| ＜1/n 或z=x}，n ∈N，為S 的子基元素;對S 的每個2 型的點z，定義以z為中心，半徑為1/n(n ∈N)的開圓盤是S 的子基元素。已知空間S 是正則Lindel?f，第一可數的cosmic 空間，但是，S不是M3-空間［6］，即S 不是Nagata－空間。S 是σ-空間，因此S 是wσ-空間。由命題3.8［7］知，第一可數的kβ-空間是wN-空間，由命題3.6［3］知，正則半分層的wN-空間是Nagata-空間，由此可知，S 不是kβ-空間。

例3 存在一個β-空間不是wσ-空間。

用R2表示平面，令Uε(x)={x}∪{y ∈R2:0＜| y1－x1| ＜ε，| m(x，y)| ＜ε}，這里x ∈R2，ε ＞0，m(x，y)表示通過x，y 直線的斜率。由上述所有水平蝴蝶結鄰域Uε(x)組成的基所生成的拓撲記為τ1，由類似的垂直蝴蝶結鄰域所生成的拓撲記為τ2。

(a)(R2，τ1)，(R2，τ2)是同胚的，它們是完全正則的半度量空間。

(b)如果Q2?Z ?R2且cardZ=2χ0，則(Z，τ1)× (Z，τ2)是非正規的。

(c)(CH)存在R2的不可數子集Z 包含Q2使得(Z，τ1)，(Z，τ2)是同胚的，且是遺傳Lindel?f 的(見例3.6［8］)。

設X 是(Z，τ1)，則X 是完全正則Lindel?f 的半度量空間。X 不是σ-空間［9］，由命題2.3［3］，X 不是wσ-空間。

4 結論

(1)文章探討了wN-空間，kβ-空間，wσ-空間和β-空間之間的關系，得到了它們之間的蘊含關系定理:wN-空間?kβ-空間，弱子序列kβ-空間?wσ-空間并且wσ-空間?β-空間。

(2)舉例說明了上述逆關系不成立，這不僅明確了這幾類廣義度量空間的關系，而且對廣義度量空間的度量化起著積極的作用。

［1］HODEL R E.Spaces defined by sequences of open covers which guarantee that certain sequences have cluster points［J］.Duke Math J，1972，39(2):253－263.

［2］吳利生.關于k-半分層空間［J］.蘇州大學學報:自然科學版，1983(1):1－4.

［3］FLETCHER P，LINDGREN W F.On wΔ－spaces，wσ－spaces and∑#－spaces［J］.Pacific J Math，1977，71(2):419－428.

［4］HOUSE V D.Countable products of generalized countably compact spaecs［J］.Pacific J Math，1975，57(1):183－197.

［5］MARTIN H W.A note on the metrization of γ-spaces［J］.Proc Amer Math Soc，1976，57(2):332－336.

［6］HEATH R W.A paracompact semi－metric space which is not an M3－space［J］.Proc Amer Math Soc，1966，17(4):868－870.

［7］XIA S X.On kβ－spaces［J］.Mathematica Japonica，1995，42(3):557－561.

［8］MICHAEL E.Paracompactness and the Lindel?f property in finite and countable Cartesian products［J］.Compositio Mathematica，1971，23(2):199－214.

［9］OKUYAMA A.Some generalizations of metric spaces，their metrization theorems and products［J］.Sci Rep Tokyo Kyoiku Daigaku Sec A，1967，9(1):236－254.

［10］YUKINOBU Y.Strong beta－spaces and their countable products［J］.Houston Journal of Mathematics，2007，33(2):531－540.

［11］殷艷敏，張明川.弱Hopf 代數上的泛R 矩陣［J］.山東建筑大學學報，2011，26(2):146－148.