基于CG-MSNWF的空時自適應抗干擾算法研究*

潘延明，盧艷娥，駱艷卜，李思佳

(空軍工程大學 電信工程學院，陜西 西安710077)

空時自適應濾波算法的優點是能夠在不增加天線陣元數目的前提下大大提高信號處理的自由度，并可以抵消諸如連續波干擾、調頻干擾等多種窄帶和寬帶干擾。在最小均方誤差MMSE(Minimum Mean Square Error)準則下，維納濾波WF(Wiener Filter)對期望信號的估計是最優的[1,2]。維納濾波僅僅依賴觀測信號的二階統計量，易于實現，因此被廣泛應用于多種場合。但是該方法需要計算觀測信號的自相關矩陣的逆矩陣，這意味著空時自適應濾波的計算量會隨著自相關矩陣維數的增加而急劇增大。因此，在當前硬件條件下，以降低計算量為目的的降秩處理是空時自適應濾波所研究的重要問題之一[3]。

針對空時自適應濾波問題，現有的降秩方法很多，其中應用最廣泛的是多級維納濾波MSNWF。相對于其他的降秩方法，MSNWF有更優的穩態和瞬態性能，能夠在處理器維數遠小于信號空間維數時，使性能接近最佳，并且避免了求解矩陣的逆、特征空間分解等復雜的運算，給計算帶來了方便[4-5]。然而，MSNWF包含前向迭代和后向迭代兩個過程，在陣元數目過多時，雙向迭代過程使MSNWF的計算量大大增加，難以滿足實時性的要求。針對這一問題，本文采用基于共軛梯度的多級維納濾波算法CG-MSNWF,該算法只有前向迭代過程，避免了開放運算，計算量小。在相同的干擾抑制性能條件下，該算法的收斂速度比MSNWF有所提高，能夠快速適應時變的場景，易于實時處理。

1 MSNWF算法

設陣列的陣元數為M,每個陣元含有P個延遲單元。信號經過M個天線陣列進入系統，數據采取分段輸入方式，數據段長度為L。這樣，每次處理的數據量為M×L維，數據經過延遲處理后轉換為N×(LP+1)維矩陣(MP=N),用X表示。處理器權向量為W，接收數據的自相關矩陣為RX=E[XXT],觀測信號與期望信號的互相關為rxd=E[Xd*]。

選擇滿秩矩陣T1=[h1]T作為預濾波,其中h1=/‖‖，B1=null(h1)稱為阻塞矩陣(Blocking Array)。

設對輸入信號X0(n)進行T1變換之后得到的信號為Z1,則：

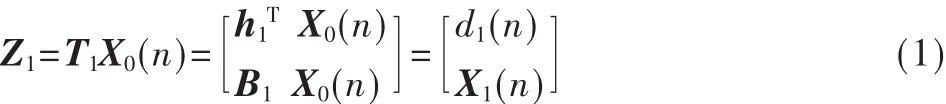
用觀測信號向量X0(n)滿秩變換后的Z1(n)來估計期望信號d0(n)，由維納濾波器的時域解可知：

由此可以看出，N維維納權可以分解為一個標量與一個(N-1)維維納權的形式，即:

其中, 標量 w1=δ1，(N-1) 維矢量為從(N-1)維矢量X1中估計標量d1的維納權。

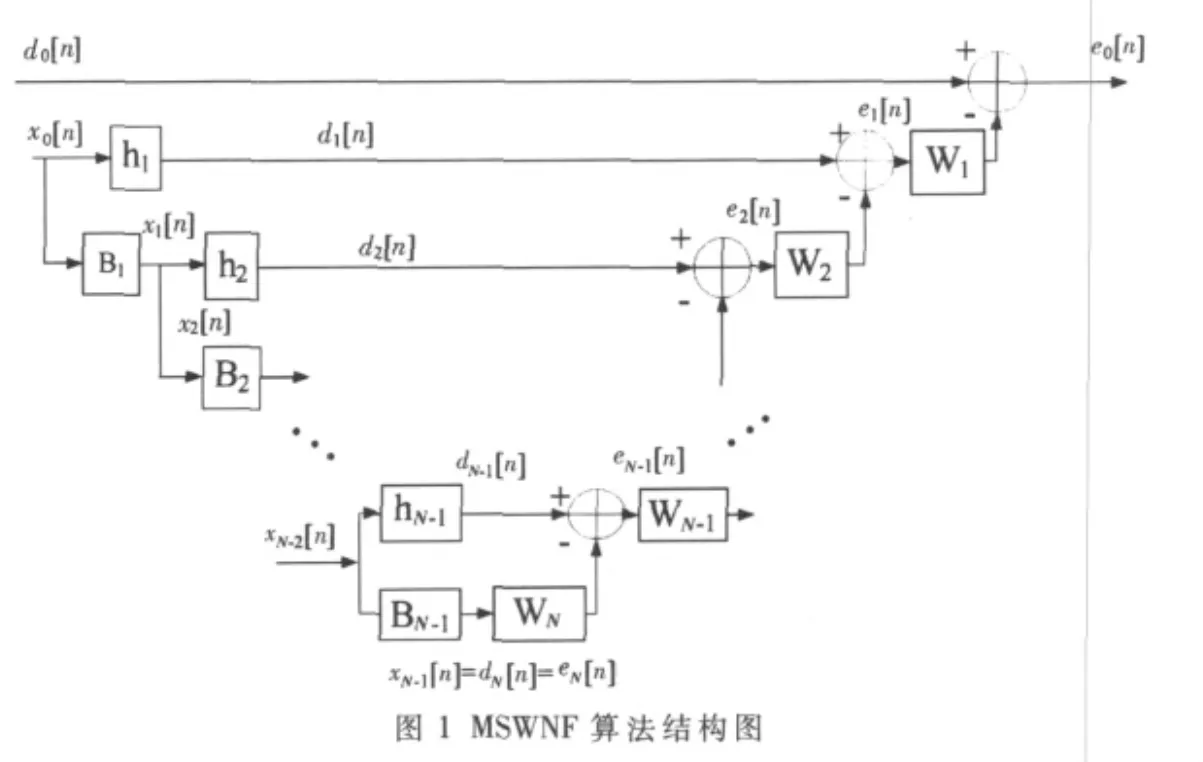
同理，繼續將 X1(n)分解，直到分解到第(N-1)級，如圖1所示。這時，XN-1(n)已經是一個標量，維數等于 1。維的維納濾波器被分解為N個級聯的標量濾波器。由式w1=α1-1δ1可知，每級標量維納濾波器的權值可由兩個標量相乘得到。

圖1表明了MSWNF降秩算法需要有前向迭代和后向迭代兩個過程，前者的作用通過將輸入信號變換到相互正交的子空間進行降秩,后者的作用是用各級的誤差信號加權來估計期望信號[6-8]。估計的誤差為：

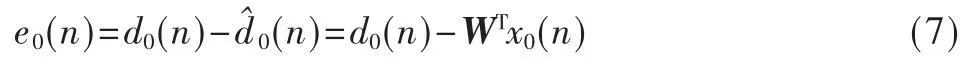
則估計的均方誤差MSE為：

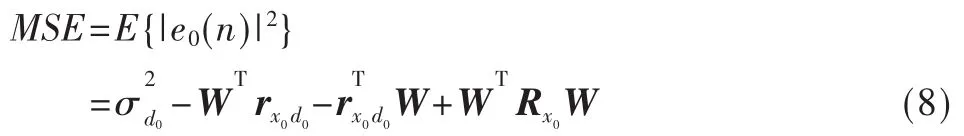
2 MSNWF改進算法

在MSNWF算法中,需要估計觀測信號的自相關矩陣，迭代的最大維數為N-1,在每次迭代時觀察最小均方誤差 αi，當迭代至 D(1≤D≤N-1)時，αi小于預先設定的MMSE門限，迭代即終止[7]。但是在迭代過程中需要反復進行開方運算,不利于硬件實現。J.Scott Goldstein等人針對 EDGE(Enhanced Data rate for GSM Evolution)系統提出一種基于共軛梯度的多級維那濾波算法CGMSNW[9],本文將該濾波算法應用于GPS接收機前端，仿真分析表明，具有很好的抗干擾效果。

2.1 共軛梯度（CG）算法

共軛梯度(CG)算法是Hestenes和 Stiefel在求解 N(N未知)階線性方程組Ax=b時所提出的[9]。求解過程是一個步迭代過程，當第D次迭代之后輸出的最小均方誤差αi小于預先設定的MMSE門限值時，迭代可以終止，此時的解向量xD是方程組的近似解。

共軛梯度算法是以下問題的解：

稱為權重因子，pi稱為導向矢量，xN是第N次迭代之后的近似解向量。

設解向量x的迭代方程為：

現在估計γi的值，使誤差函數f(x)取得最小，可得：

第i-1次迭代之后的剩余誤差為：

將式(12)代入式(14)可得：

2.2 基于CG的MSNWF算法

關于MSNWF和CG算法的分析比較，參考文獻[9，10]給出了詳細的論述。下面直接給出CG-MSNWF的算法流程：

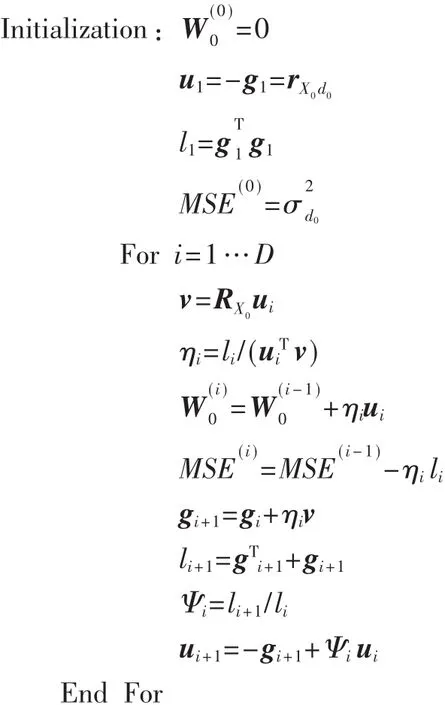
比較CG-MSNWF和MSNWF兩種算法可以發現，前者不僅實現簡單，而且在迭代運算中避免了開方運算，既不需要后向迭代，也不需要計算阻塞矩陣B,從而簡化了運算過程，提高了運算效率。因此，本文采用CGMSNWF算法作為求解維納濾波器權系數的方法。

3 仿真分析

為了充分驗證CG-MSNWF算法的有效性和可靠性，本文對算法的干擾抵消和收斂情況進行了仿真。

3.1 CG-MSNWF對干擾抵消情況

采用陣元數為M=7的均勻線性天線陣，每個天線陣的延遲為P=4。接收機處理帶寬B=20 MHz，中頻 IF=46.52 MHz，采樣率 FS=65.536 MHz。GPS信號的信噪比S/N=-15 dB，DOA為 30°，設 PRN碼偏移量為 0。設干擾個數為10個，如表1所示。

采用CG-MSNWF處理前后的信號頻譜圖如圖2所示。經過CG-MSNWF算法的輸出信號中干擾成分已被有效抑制，在輸出信號的頻譜中，單頻干擾和寬帶干擾均被抵消掉，其中在單頻干擾信號的頻點處產生凹陷，凹陷的幅度約為10 dB，達到了抗干擾的目的。

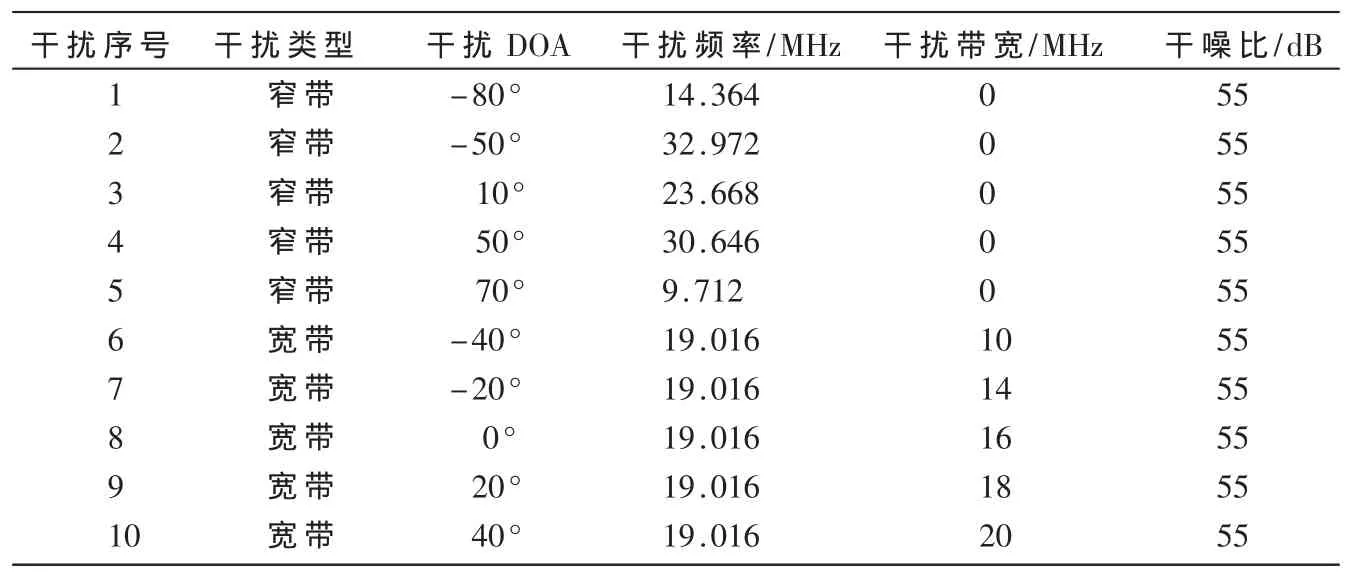
表1 干擾信號信息表

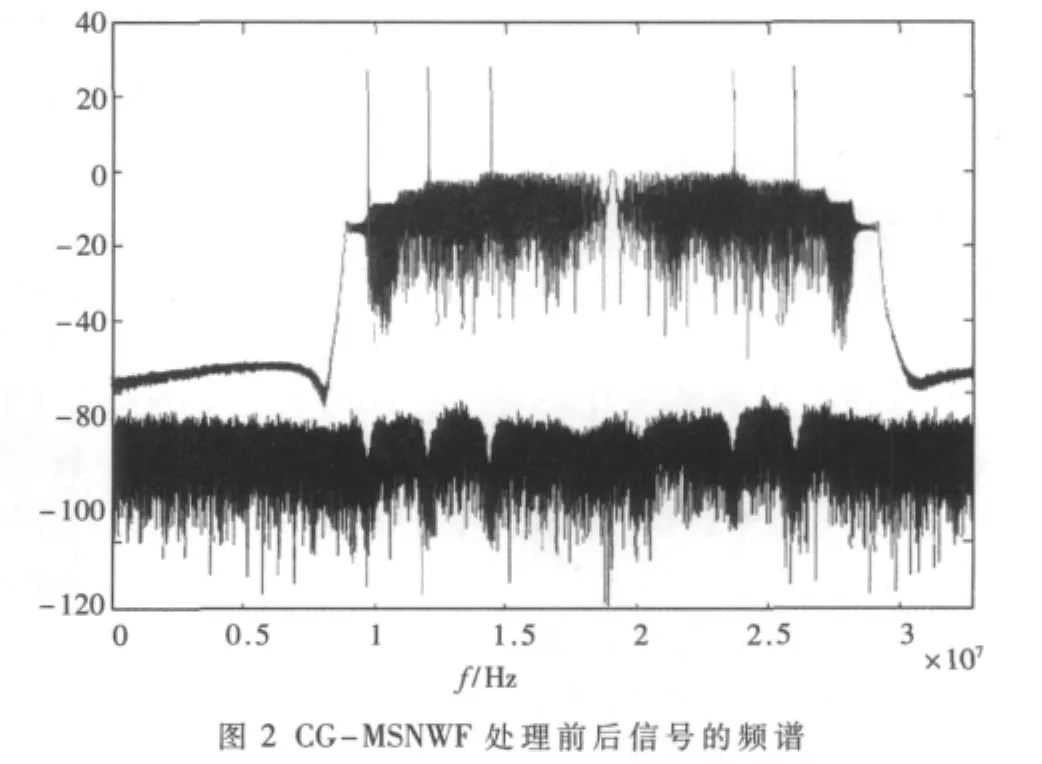
在實際應用中，用PRN自相關的最大峰值與次大峰值的比值[11]來檢驗算法對干擾的抵消情況，判斷是否可以檢測到GPS信號，其經驗判決門限為最大峰值與次大峰值之比等于1.5 dB。在本次仿真試驗中，根據圖3所示，該比值為4.57 dB，所以經過CG-MSNWF算法處理之后,可以檢測到GPS信號,從而證明了算法的有效性。

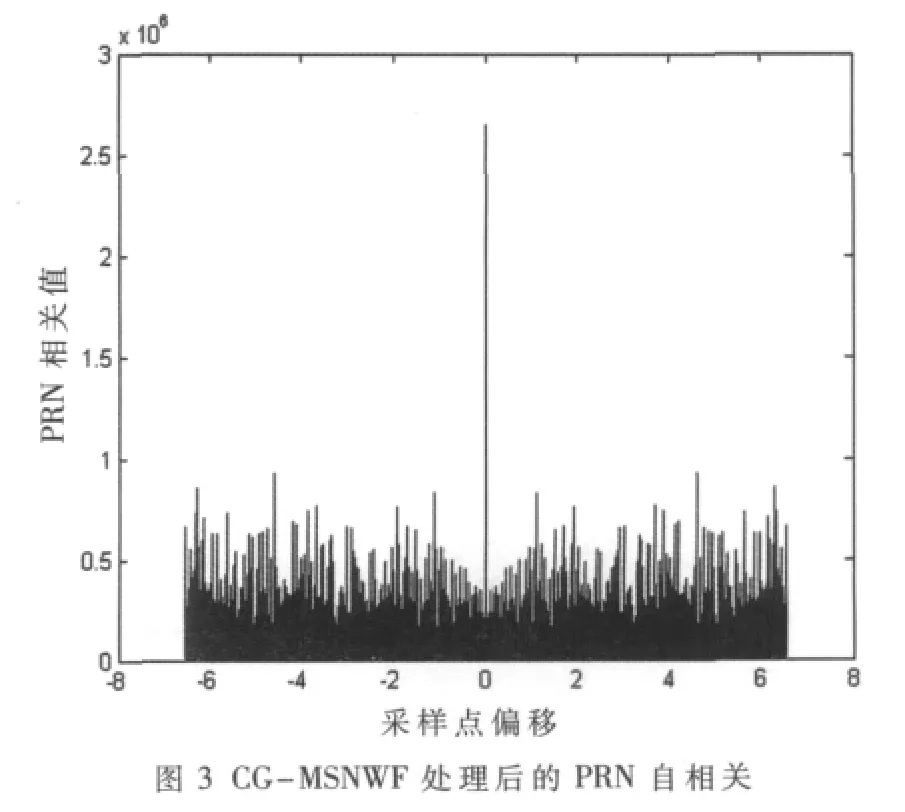
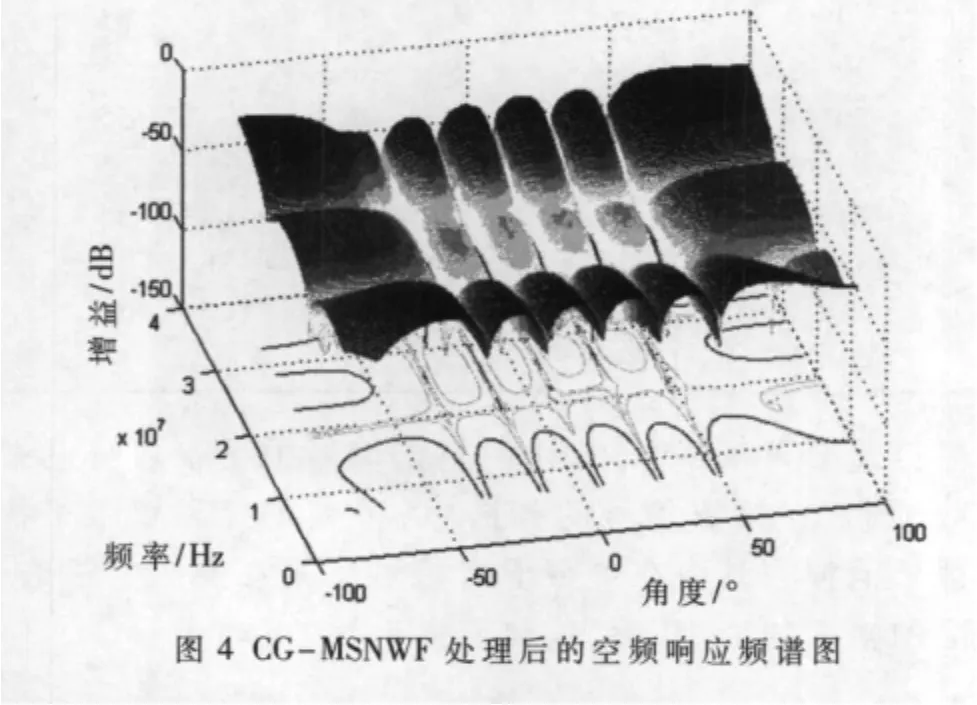
圖4為濾波輸出信號的空頻響應，可見在與表1所對應的干擾DOA和干擾頻率(頻帶)處產生凹陷，進一步證明了該算法對干擾抵消的效果是非常理想的。

3.2 CG-MSNWF的降秩和收斂性能

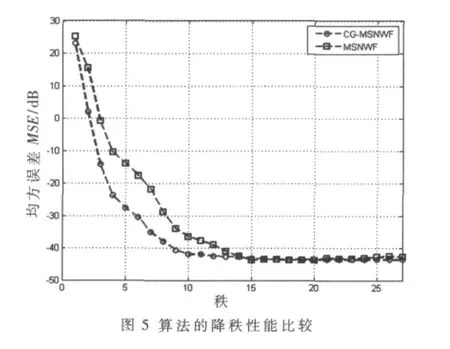
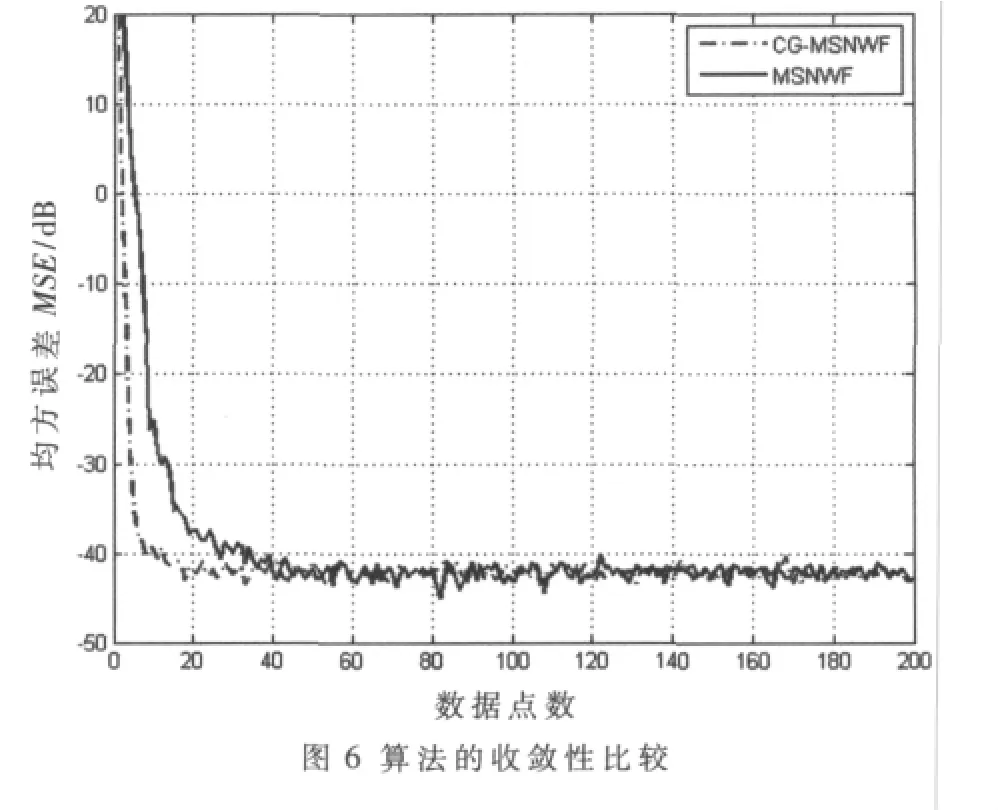
對MSNWF算法的研究表明,MSNWF是一種降秩自適應濾波方法，該算法使系統在秩遠小于信號子空間秩的時候趨于收斂[4,5]。CG-MSNWF是MSNWF基于共軛梯度的改進算法，也是一種降秩自適應濾波方法。CGMSNWF算法不需要后項迭代過程，運算簡單，降秩性能好，從而大大降低了計算量，提高了收斂速度。圖5和圖6分別給出了兩種算法降秩性能和收斂性能比較。可以看出，CG-MSNWF算法在系統的秩R=10時就趨于收斂，降秩性能優于MSNWF算法；系統達到穩態的秩減小了，說明算法的計算量有所減小，實時性有所增加，能夠快速適應時變的場景。

本文針對MSNWF算法計算量大，在處理高維數據時，不能滿足實時性要求這一問題，采用基于共軛梯度的改進算法——CG-MSNWF，該算法是一種降秩自適應算法，省略了后項迭代過程，計算簡單，可以使系統在秩R=10的時候就趨于收斂，且性能與滿秩時相差不大，從而克服了其他空時自適應濾波算法的計算量大的弱點，增強了抗干擾的實時性。本文對該算法的有效性和可靠性進行了仿真,仿真結果證明了該算法的合理性。

[1]盧艷娥.“北斗一號”用戶接收機自適應抗干擾天線半物理仿真系統關鍵技術研究[D].北京：北京航空航天大學博士學位論文，2004.

[2]高增來,盧艷娥.空時自適應抗干擾算法分析與仿真[J].通信技術，2007，40(12)：174-176.

[3] 盧艷娥，談展中.用于雙衛星導航系統用戶接收機抗干擾的自適應干擾正交約束下的最佳信號增強算法[J].電子學報，2004，32(8)：1239-1243.

[4]GOLDSTEIN S J,REED I S.Reduced-rank adaptive filtering[J].IEEE Transactions on Signal Processing 45,February 1997：492-496.

[5]GOLDSTEIN S J,REED I S.SCHARF L L.A multistage representation of the wiener filter based on orthogonal projections[J].IEEE Transactions on Information Theory,1998,44(7):2943-2959.

[6]司曉東，蔚保國.GPS接收機空時二維抗干擾技術研究[J].測控遙感與導航定位，2010，40(3)：34-35.

[7]王永良，丁前軍，李榮鋒.自適應陣列處理[M].北京：清華大學出版社，2009.

[8]周柱，石峰，張爾揚，等.一種GPS接收機級聯抗干擾方法[J].信號處理，2010，26(9)：56-62.

[9]DIETL G.Conjugate gradient implementation multi-stage nested wiener filter for reduced dimension processing[M].Munich University of Technology Institute for Circuit Theory and Signal Processing.2001.

[10]DIETL G,ZOLTOWSKI M D,JOHAM M.Reduced-rank equalization for EDGE via conjugate gradient implementation of multi-stage nested Wiener filter[C].IEEE 2001 VTC.VTS.2001：1912-1916.

[11]鄔迪，陳庭燕.基于通用相關器的高動態GPS信號并行快速捕獲[J].清華大學學報,2007,47(11):2064-2067.