兩輪不平衡小車變結構控制抖振與魯棒性研究

何雅靜，屈勝利，孟祥忠，秦 星

(西安電子科技大學，陜西 西安 710071)

兩輪不平衡小車是一個集環境感知、動態決策與規劃、行為控制與執行等多種功能于一體的綜合系統。它的動力學方程是一個多變量、耦合、時變的非線性高階方程，加上運動學方程中的非完整約束，使它成為一個具體的、實現起來相對簡單的系統。近年來，兩輪不平衡小車作為一個理論與實踐相結合的系統，受到高度重視，它是檢驗各種控制方法處理能力的典型裝置[1]。針對以往[2]通過反饋線性化得到小車系統的線性模型，然后在指數趨近律基礎上進行變結構控制的方法，消抖效果并非很好，而且在削弱系統抖振的同時也削弱了系統的抗干擾能力。為此，本文首先基于飽和特性的準滑模指數趨近律設計出了常規切換面滑模控制器和動態切換面滑模控制器。該控制器較以前的方法更有效地削弱了系統的抖振；然后通過給飽和特性的準滑模指數趨近律中加入擾動跟蹤項，設計出了帶擾動跟蹤項的動態切換面準滑模控制器。該控制器不僅很好地削弱了系統抖振，增大了系統的可控范圍,更重要的是很好地保證了系統的魯棒性。

1 小車系統建模及其反饋線性化

設電機的力矩系數為 km，反電動勢常數為 ke，電機電阻為 R，轉子慣量為 J，接入減速箱的減速比為 kj;小車車體質量為Mp，車輪及軸的質量為Mw，車體質心到車體轉動中心距離為l，車輪半徑為r，車體轉動慣量為Ip，車輪及軸轉動慣量為Iw，重力加速度為g，車輪水平位移為x1，水平速度為 x2，車體偏離垂直方向的角度為 x3，偏離垂直方向角加速度為x4，整個系統的輸入即電機的輸入電壓為u。

取狀態變量X[x1x2x3x4]T，將電機的輸入電壓u作為控制信號。為了便于研究，把系統看作線性化的單輸入單輸出系統。由于角度對系統的影響最大，所以將角度x3作為輸出，它可由傾角傳感器測得[1]。根據力學建模得到系統的非線性方程為[3]：

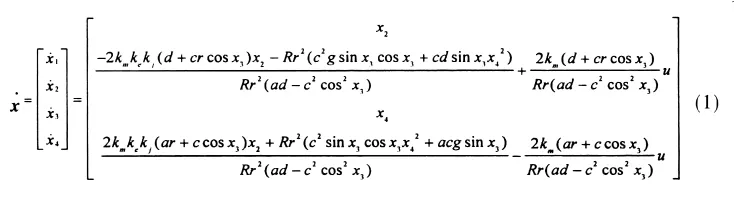
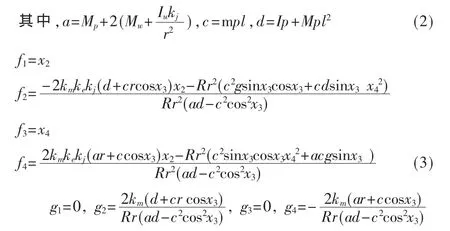
由“相對階定理”得知：該小車模型只能局部線性化。采用“李理論”方法，根據非線性控制理論[4]，取反饋控制律 u：

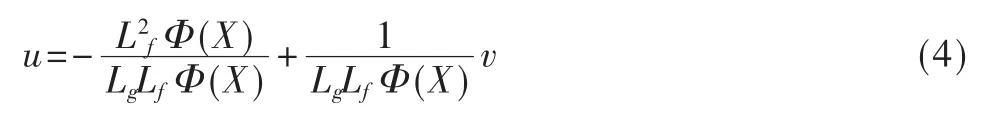
其中v(x)是u的擴展輸入。為了設計方便，取Φ(X)=x1，令，v=v0+x3由式(3)、式(4)得非線性狀態反饋控制器：

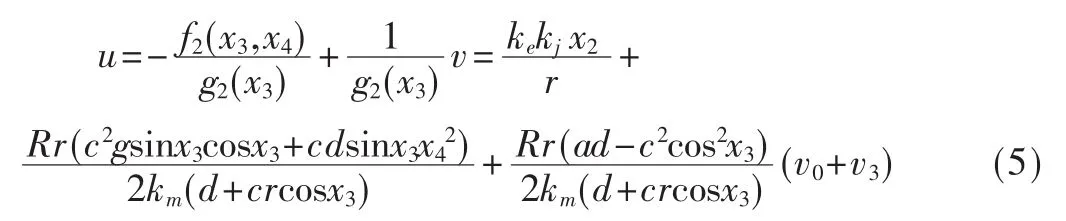
將式(5)代入式(1)，可得：

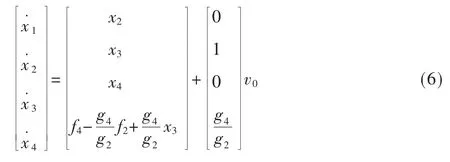
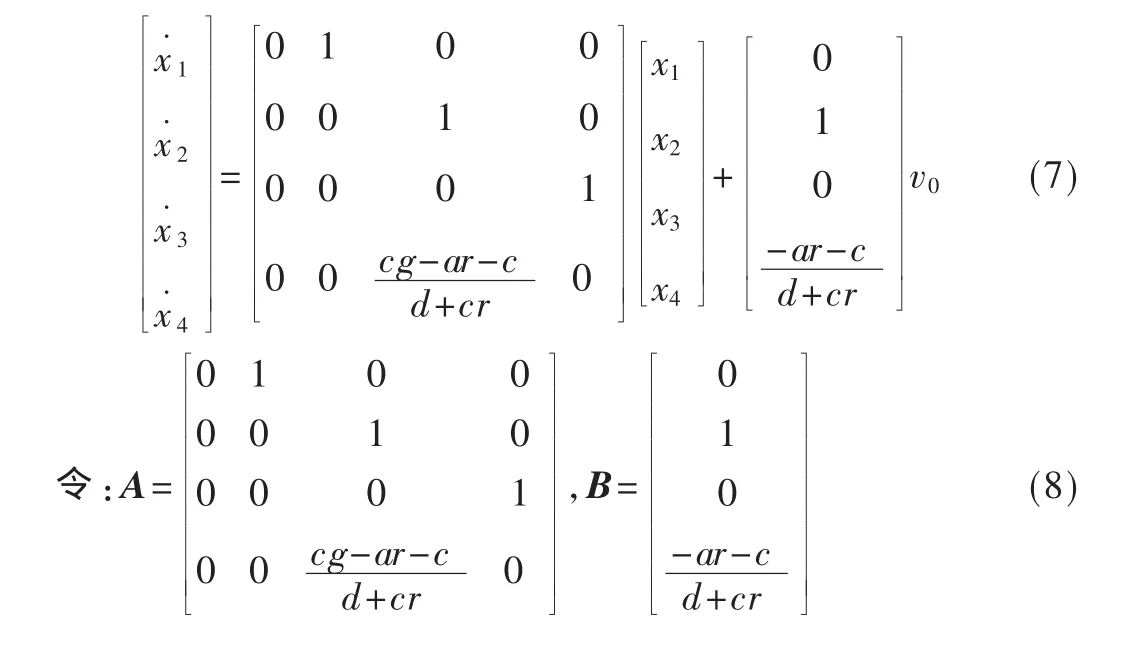
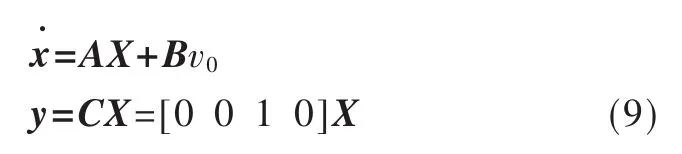
2 不平衡小車的變結構控制器設計[5-7]

為驗證小車系統可控，通過式(8)設計 LQR(線性二次型最優)控制器，得到狀態反饋陣：

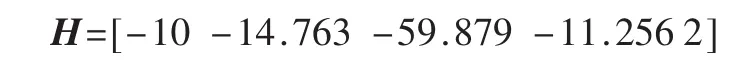
準滑動模態是指系統的運動軌跡被限制在理想滑動模態的某一領域（滑動模態切換面的邊界層）內的模態。在邊界層內，準滑動模態不要求在切換面上進行控制結構的切換，這就已經從根本上削弱了抖振。取飽和特性的準滑動模態指數趨近律為：

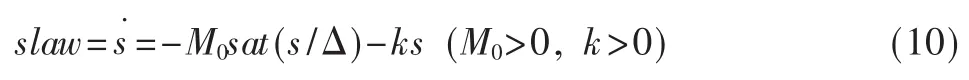
其中，M0為系統趨近切換面的速度，當 M0很小時，調節過程太慢；當M0較大時，到達切換面時系統速度較大，必然引起抖振。線性項保證系統的運動軌跡按指數趨向切換面，從而保證過渡過程有較好的品質，減小抖振。

2.1 基于常規切換面的準滑模控制器的設計

根據變結構理論，常規切換面的選取只依賴于系統的狀態，而與系統的輸入無關。對于本小車系統,設其切換面為：

聯立式(5)、式(10)可得到基于常規切換面的準滑模控制器：

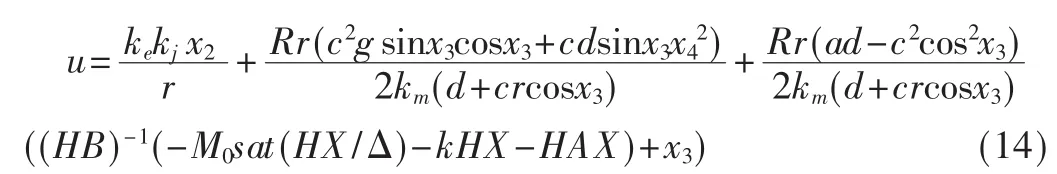
由式(5)可以看到：不連續項 M0sat(HX/Δ)直接含在控制u中，當系統運動到滑模區時，會在不同的控制之間來回切換，引起抖振。

2.2 基于動態切換面的準滑模控制器的設計

根據變結構理論：動態滑模切換面使切換函數與系統控制輸入的一階或高階導數有關，這樣可將不連續項轉移到控制的一階或高階導數中去，得到在時間上本質連續的動態滑模控制律，從而降低抖振。

針對小車系統，設計其動態切換面為：

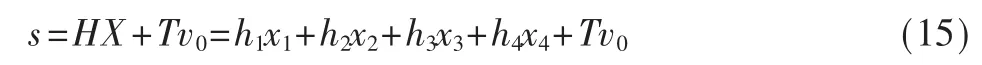
準滑模指數趨近律仍為：

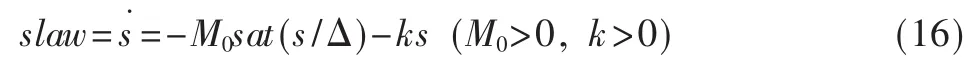
對式(15)求導，將式(9)代入，并聯立式(16)，同 2.1節的計算方法，可得：

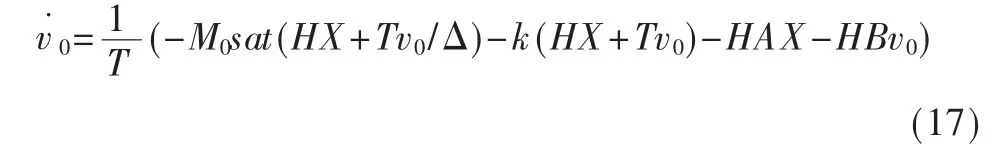
對式(17)積分代入式(5)，即得到基于動態切換面的準滑模控制器：

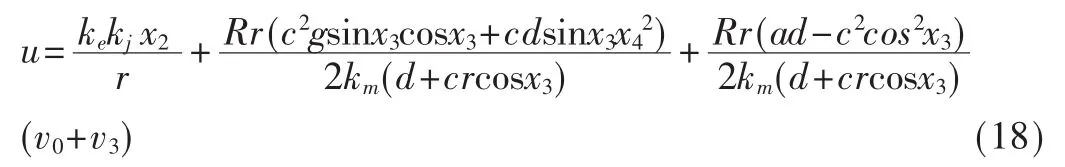
顯然，動態切換面是在常規切換面中加入與控制輸入有關的Tv0項，使得不連續切換項M0sat(HX/Δ)轉移到控制的一階導數v˙0中。因為控制u中不存在不連續切換項，所以有效地降低了抖振。

2.3 帶擾動跟蹤的動態滑模控制器的設計

由于以往的方法在消抖的同時也削弱了系統的抗干擾能力，而擾動的存在會惡化系統的性能。在滑模控制中，擾動會使本來位于滑動面的運動偏離滑動面。從幾何學角度可以將該擾動分解為兩個方向：沿滑動面的切線方向和垂直于該切線的法線方向。從物理學角度,分解在沿滑動面切線方向的擾動將給系統一個繼續沿滑動面運動的加速度，它對系統的影響不大；而分解在垂直于滑動面方向的擾動會給系統一個垂直滑動面方向的加速度，也就是擾動引起系統在滑動面垂直方向上產生遠離滑動面的加速度，使系統脫離滑動面。為了避免擾動造成系統運動偏離滑動面過大，本文在飽和特性的指數趨近律中加入擾動動力跟蹤項來減小系統遠離滑動面運動的加速度，以增強系統的抗干擾能力。

根據上面的分析，擾動會引起系統在垂直滑動面方向的加速度，故根據位置加速度計測得的位置加速度x˙1在垂直滑動面方向的分量 λx¨1(0≤λ≤1)來克服擾動在垂直滑模運動方向上的加速度。在基于飽和特性的準滑模指數趨近率基礎上設計帶擾動跟蹤項的趨近律為：

對式(22)積分，代入式(5)，得到帶擾動跟蹤項的動態切換面滑模控制器：

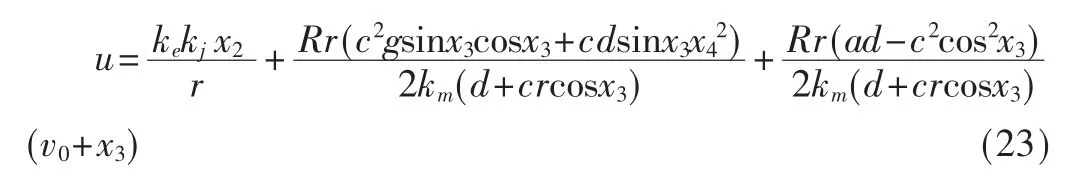
3 仿真比較[8]

由maxon電機手冊得到：額定電壓為30 V,力矩系數km=0.0389 Nm/A,電機電阻R=1.23 Ω,轉子慣量J=0.000 065 5 kgm2，反電動勢常數ke=1/246=0.004 065 V/rpm,接入減速箱的減速比 kj=33,測量得小車車體質量為Mp=10.36 kg，車體質心到車體轉動中心距離l=0.2 m,車輪及軸質量Mw=0.4 kg，車輪半徑r=0.06 m，車輪及軸轉動慣量Iw=0.000 36 kg·m2，車體轉動慣量 Ip=0.037 59 kg·m2，取重力加速度g=9.81 N/kg。

3.1 可控范圍的比較

取 M0=20，k=10，T=0.5，G=0.3,在小車位置、速度、角速度全都為0的情況下,通過不斷變換角度初始值，觀察控制電壓為額定值時的角度值即為小車在此控制器下的最大可控傾角。仿真得到如表1所示的三種控制器的最大可控傾角。

表1 三種控制器的最大可控角

由表1可以看出，系統在帶擾動跟蹤項的動態切換面滑模控制器作用下的可控角最大，動態切換面準滑模控制器次之，而常規切換面準滑模控制器作用下系統的可控角最小。下面對三種控制器控制效果的比較都在其傾角可控范圍內。

3.2 系統抖振的比較

根據變結構理論：系統運動在滑模區時，其特性和參數只取決于切換函數而與其他無關，即滑模具有完全魯棒性。但伴隨滑模的運動,系統會出現抖振，這種高頻振動會嚴重影響系統的性能。下面就上文所設計的三種不同控制器作用系統時所產生的抖振進行觀察比較。

仍取初始狀態X=[0 0 0.45 0]T，其他參數不變，在三種不同控制器控制作用小車角度在10 s內的響應曲線如圖1示。

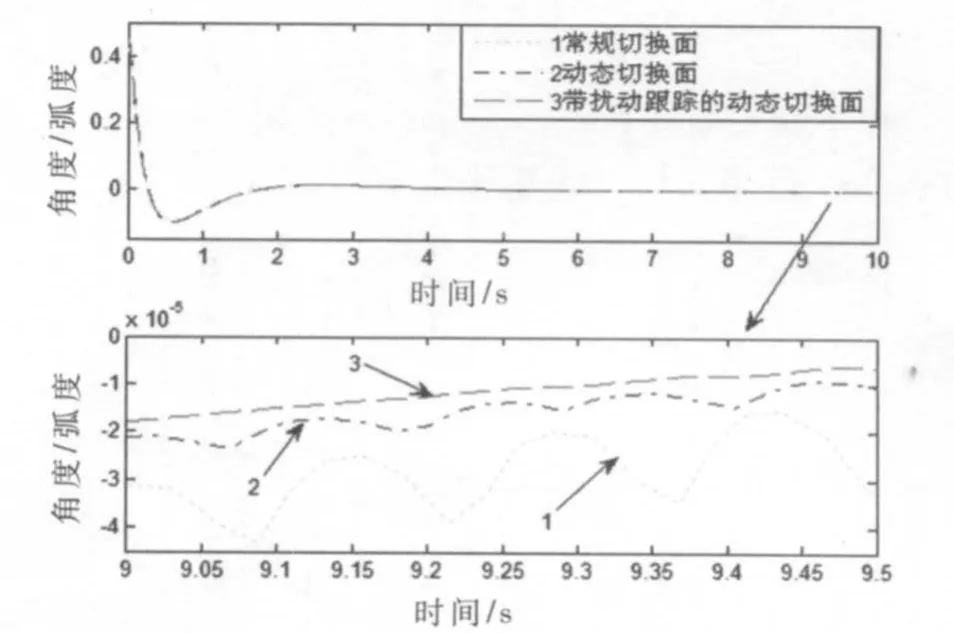
圖1 小車角度響應的比較

由圖1可看出，在三種不同控制器的作用下，系統的位置、速度、角速度以及控制u響應曲線都有圖1所示的特性，即動態切換面滑模控制器比常規切換面滑模控制器在消抖方面有明顯的優勢，而帶擾動跟蹤的動態切換面滑模控制器比不帶擾動跟蹤的動態切換面滑模控制器在消抖方面有明顯的優勢。

3.3 系統抗干擾性比較

設小車位于平衡狀態X=[0 0 0 0]T處，給系統的控制輸入端u處加入幅值為5的隨機干擾信號，在上述三種不同控制器作用下小車速度在3 s內的響應曲線如圖2示。

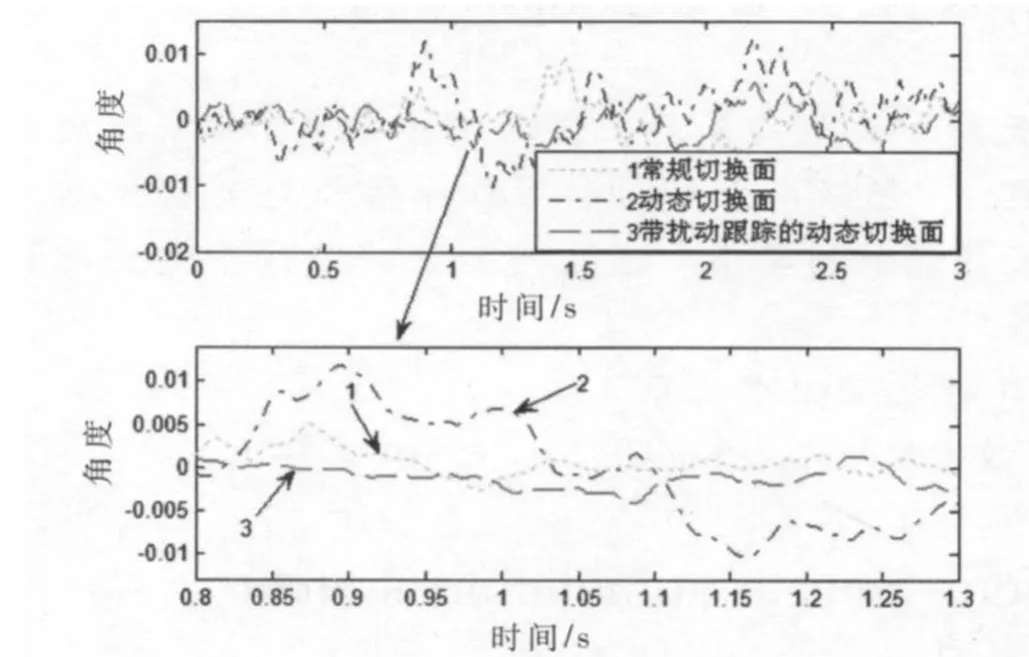
圖2 干擾作用下的小車角度響應比較

由圖2可看出，對于系統角度，動態切換面滑模控制器作用下系統的抗干擾能力比常規切換面滑模控制器作用下系統抗干擾能力弱很多，但是通過增加擾動跟蹤項,可使動態切換面滑模控制器的抗干擾能力又得以顯著地增強。

大量仿真曲線表明：對于相同的趨近律，與常規切換面滑模控制器相比，動態切換面滑模控制器雖然顯著地削弱了系統的抖振，但同時也削弱了系統的抗干擾能力。而通過給趨近律中加入擾動跟蹤項設計的帶擾動跟蹤的動態滑模控制器作用系統時，不僅顯著地削弱了系統的抖振，而且保留了常規切換面滑模控制器較強的抗干擾能力。由此可見，擾動跟蹤項不但很好地補償了變結構控制的抖振缺陷，而且還實現了系統對擾動的不變性，增大了系統的可控范圍。

本文針對反饋線性化得到的小車系統線性模型，設計了基于常規切換面和動態滑模切換面的準滑動模態變結構控制器，并在此基礎上通過給控制u中加入擾動跟蹤項，設計出能同時削弱抖振和保證系統抗干擾能力的控制器，實現了小車的穩定控制。通過仿真比較可以看出，與常規切換面控制器作用相比，在基于動態切換面控制器作用下系統的可控范圍較大、抑制系統抖振能力強，但同時系統的魯棒性變差，即在削弱系統抖振的同時也削弱了系統的魯棒性。而通過給控制u中加入擾動跟蹤項使系統抗干擾能力顯著增強，即具有擾動跟蹤的動態滑模控制器不僅更好地削弱了系統的抖振，同時還保證了滑模對擾動的不變性，實現了滑動模態魯棒性和消除抖振的統一。

[1]Li Yanzhao,Qu Shengli,Zhu Jiahui,et al.Study on the control of a two-wheeled unstable vehicle based on sensitivity Analysis[M].The University of Western Australia School of Mechanical Engineering,IEEE,2009.

[2]OOI R C.Banlancing a two-wheeled autonomous robot[M].IEEE,2003.

[3]朱加輝.兩輪自平衡小車反饋線性化及變結構控制研究[D].西安:西安電子科技大學，2010.

[4]胡躍明.非線性控制系統理論與應用[M].北京：國防工業出版社，2005.

[5]高為炳.變結構控制理論基礎[M].北京：中國科學技術出版社，1990.

[6]姚瓊薈.變結構控制系統[M].重慶：重慶大學出版社，1997.

[7]趙勇.兩輪不穩定機器人載體運動學及動力學變結構控制研究[D].西安：西安電子科技大學，2007.

[8]黃忠霖.控制系統MATLAB計算及仿真[M].北京：國防工業出版社，2004.