重力壩壩踵應力控制標準的研究

楊清平，李俊杰

（大連理工大學，遼寧 大連 116023）

隨著計算機技術的飛快發展，有限元計算方法也得到了迅猛的發展，已經廣泛的運用在各個領域。但用有限元方法求解重力壩壩踵應力時，得不到準確解，應力在此失真，即隨網格的不同，應力在壩踵區有明顯的差別。然而，重力壩設計規范是根據材料力學解出的，有限元方法沒有相配套的設計標準。加之，影響重力壩壩踵應力的因素很多，例如基巖特性、壩體材料分區、地基與壩體彈模比、揚壓力等，所以到目前為止，重力壩壩踵應力控制標準一直沒有得到很好的解決。在閱讀文獻[1]、文獻[2]的基礎上，作者做了一些有意義的工作。由于影響因素眾多，本文的計算荷載僅考慮水平水壓力和壩體自重，為進一步研究其他工況打下一定的基礎。在此引入壩踵主應力區相對寬度的概念，定義壩踵主應力區相對寬度brL為壩踵主應力區寬度b與壩體底寬B的比值，用公式表示為brL=b/B×100%。

1 計算工況和網格剖分

1）壩高。為了考慮在不同壩高的情況下，網格剖分的不同對壩踵應力分布規律的影響，本文計算了幾種壩高的重力壩，其壩高分別為80，110，160，190 m。其典型斷面和計算水位如圖1所示。

2）壩體下游邊坡。為了考慮在不同壩體下游邊坡的情況下，網格剖分的不同對壩踵應力分布規律的影響，對于每種壩高分別進行了3種邊坡的計算，3 種邊坡的大小分別是 1∶0.70，1∶0.75，1∶0.80。

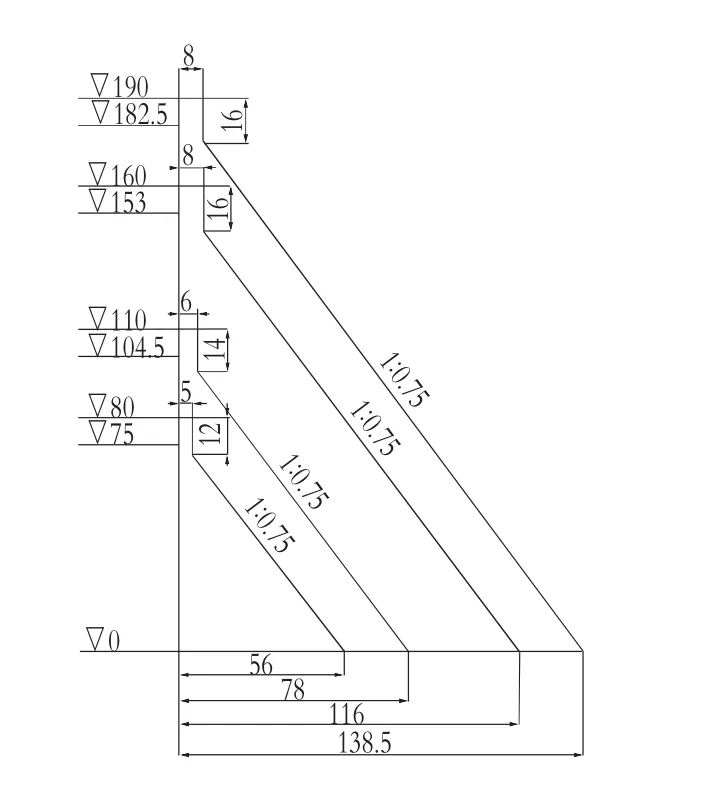
圖14種壩高的典型斷面和計算水位圖

3）壩基與壩體彈模比。為了考慮在不同壩基與壩體彈模比的情況下，網格剖分的不同對壩踵應力分布規律的影響，對每種壩高、每種邊坡計算了3種彈模比的計算，3種彈模比大小分別是0.5，1.0，2.0。對于160 m 的高壩進行了6種彈模比的計算。6 種彈模比分別為 0.5，1.0，2.0，4.0，8.0，10.0。

4）地基剖分區域。為了使計算的結果盡可能的接近實際的情形，在剖分壩基時，壩基上下游剖分長度分別為3倍的壩高，壩基剖分深度為三倍的壩高。

5）地基及壩體網格加密區域。根據以往作的研究表明，一般情況下，重力壩壩踵主拉應力區的相對寬度約為21%，主拉應力區的相對高度約為7%。基于這些結果，壩踵處加密區域采用水平向為壩底寬度的30%，加密區域豎向高度約為壩高的10%。并且，與壩踵及建基面相鄰的地基也進行了加密。

6）網格尺寸。由于有限元方法在分析應力奇異點時，結果失真，網格剖分的不同對結果的影響很大，因此本文在計算時把加密區域的網格分為28組，便于分析網格對應力奇異點的影響。由于數據量很大，本文選用160 m高的壩，網格剖分數據見表1。

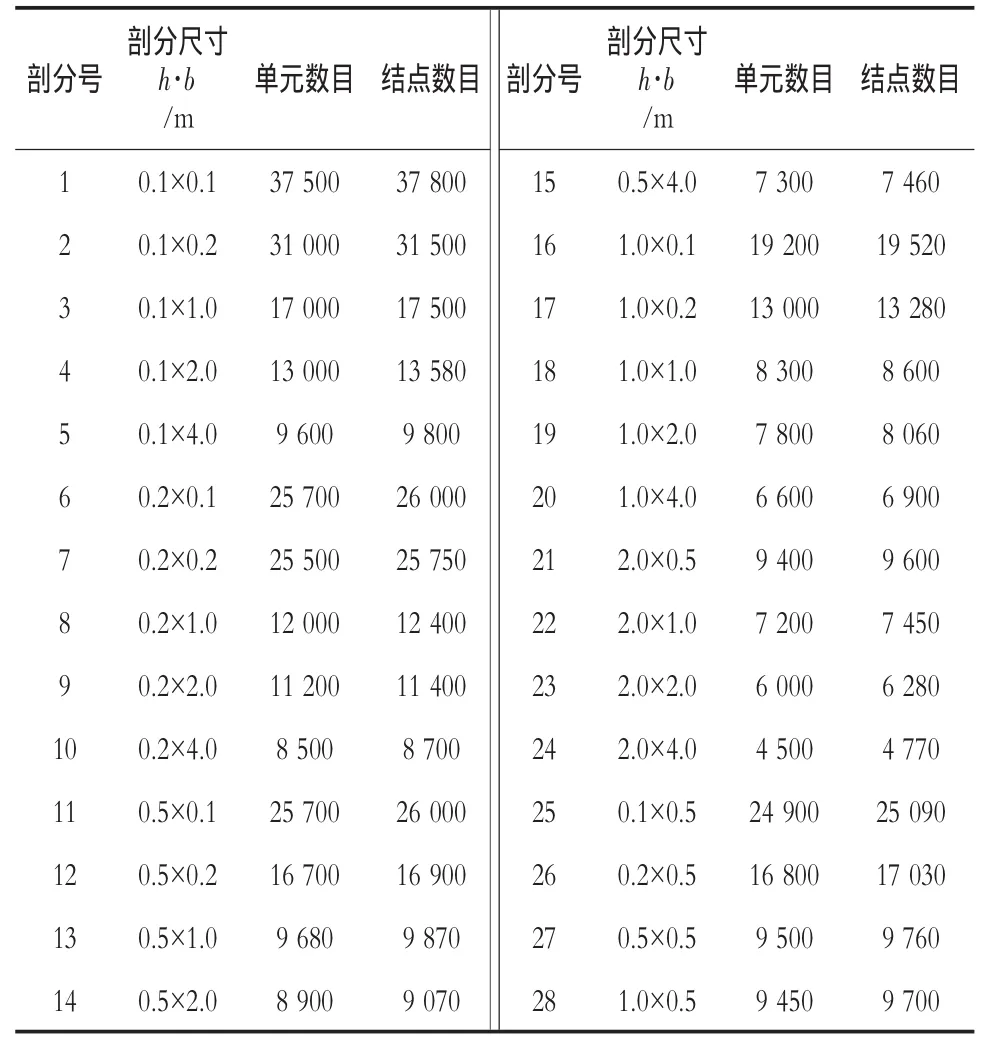
表1160 m高壩網格剖分信息

2 計算參數

由于工況很多，本文采用線彈性的有限元模型進行計算，取壩體混凝土容重γ=23544 N/m3，泊松比μ=0.17，彈性模量Ed=2×1010Pa。取地基容重 γ=0 N/m3，泊松比 μ=0.20，彈性模量 Ef=4×1010Pa。壩體與地基剪切模量按照公式轉換。

3 網格對壩踵主拉應力分布規律的影響

通過對不同壩高、不同下游邊坡、不同地基與壩體彈模比的情況，分別進行了28組網格的計算，計算結果表明：不同情況下，網格對壩踵主拉應力的影響表現出一致性和穩定性。

對于110 m壩、190 m壩，選取下游邊坡為1∶0.75、地基與壩體彈模比為1.0的5組網格的計算結果分別繪于圖2和圖3中。

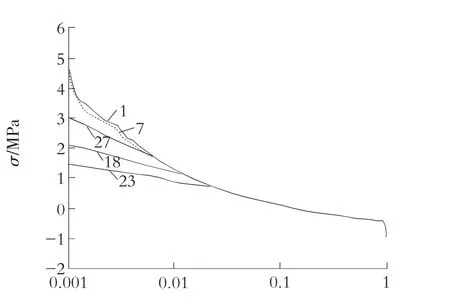
圖2110 m壩五組網格計算的沿壩建基面相對寬度的變化曲線

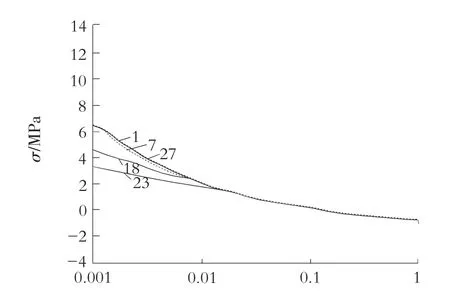
圖3190 m壩五組網格計算的沿壩建基面相對寬度的變化曲線

由圖2和圖3可以看出，在沿建基面距壩踵一定范圍之外，網格剖分的不同對主應力的分布規律的影響非常小，基本可以忽略不計。在沿建基面壩踵主拉應力區的范圍內，網格剖分的不同對主拉應力的大小和分布有一定的影響，在沿建基面距壩踵較小的范圍內，主拉應力隨網格剖分的不同有較大的差異（見表2）。從表2中可以看出，對于110 m高壩，7號網格在壩踵處主拉應力值為5.31 MPa，23號網格在此處的主拉應力值為1.45 MPa，兩者相差了3.86 MPa；對于190 m高壩，1號網格在壩踵處主拉應力值為13.48 MPa，23號網格在此處的主拉應力值為3.14 MPa，兩者相差了10.34 MPa。如果用沿壩建基面相對寬度來度量，從圖1和圖2中也可以看出在距壩踵的相對寬度值大約為7%的范圍以外，網格剖分的不同對主應力的分布規律的影響非常小；在距壩踵的相對寬度值大約為7%的范圍以內，主拉應力隨網格剖分的不同有較大的差異。網格剖分的越細，主拉應力在壩踵處的值也越大，其應力遞減梯度也越大。但網格剖分的不同對壩踵的主拉應力區相對寬度影響較小。也就是說，壩踵的主拉應力區相對寬度相對于壩踵網格剖分的不同是較為穩定的。

4 重力壩壩踵應力控制標準的研究

通過以上的分析，可以知道：網格剖分的不同對主應力的大小和分布沿整個建基面都有不同程度的影響，從壩踵到壩趾這種影響依次減弱，不同網格之間的誤差在距壩踵較近的區域內遞減很快。為了研究這個問題，取80，110，160，190 m等4種不同的壩高、3種不同的地基與壩體彈模比0.5,1.0,2.0、下游邊坡1∶0.75多種不同網格的計算結果來進行分析，為了研究方便，定義主應力σ1的絕對誤差為：在沿建基面距壩踵等距的地方，不同網格計算的主應力值σ1i與這些主應力平均值的差值的最大值，用公式表示為，其中ea為主應力σ1在建基面某處的絕對誤差，在這里，n=28。定義主拉應力σ1相對誤差為：主應力σ1絕對誤差與主應力平均值的比值，用公式表示為，其中，er為主應力σ1在建基面某處的相對誤差。

表2110，190 m高壩在不同網格下主應力相對寬度和對應的值

采用相同壩高，相同地基與壩體彈模比的不同網格之間的主應力σ1的相對誤差來研究重力壩壩踵應力控制標準。本文取了7種主應力σ1的相對誤差作為控制標準和他們對應的建基面相對寬度來分析不同網格之間的差距，其結果見表3。

從表3中數據可以得出：

1）地基與壩體彈模比的不同對網格剖分的影響。對于相同的壩體，不同的網格，在相同的主應力σ1的相對誤差的控制下，地基與壩體的彈模比越大，大于該項誤差的主應力σ1的分布區域越小。地基與壩體的彈模比越小，大于該項誤差的主應力σ1的分布區域延伸的越遠。甚至沿整個建基面都大于該項誤差。也就是說，隨著地基與壩體彈模比的增大，網格剖分的不同對主應力沿建基面的分布和大小的影響相對減弱。

2）壩高的不同對網格剖分的影響。對于相同的地基與壩體的彈模比，不同的壩高，在相同的主應力σ1相對誤差的控制下，壩體越高，大于該項誤差的主應力σ1的分布區域沿建基面相對寬度越小，并且沿整個壩基的主應力σ1的分布是很穩定的。也就是說：壩體越高，網格剖分的不同對主應力σ1沿建基面的分布和大小的影響相對減弱。

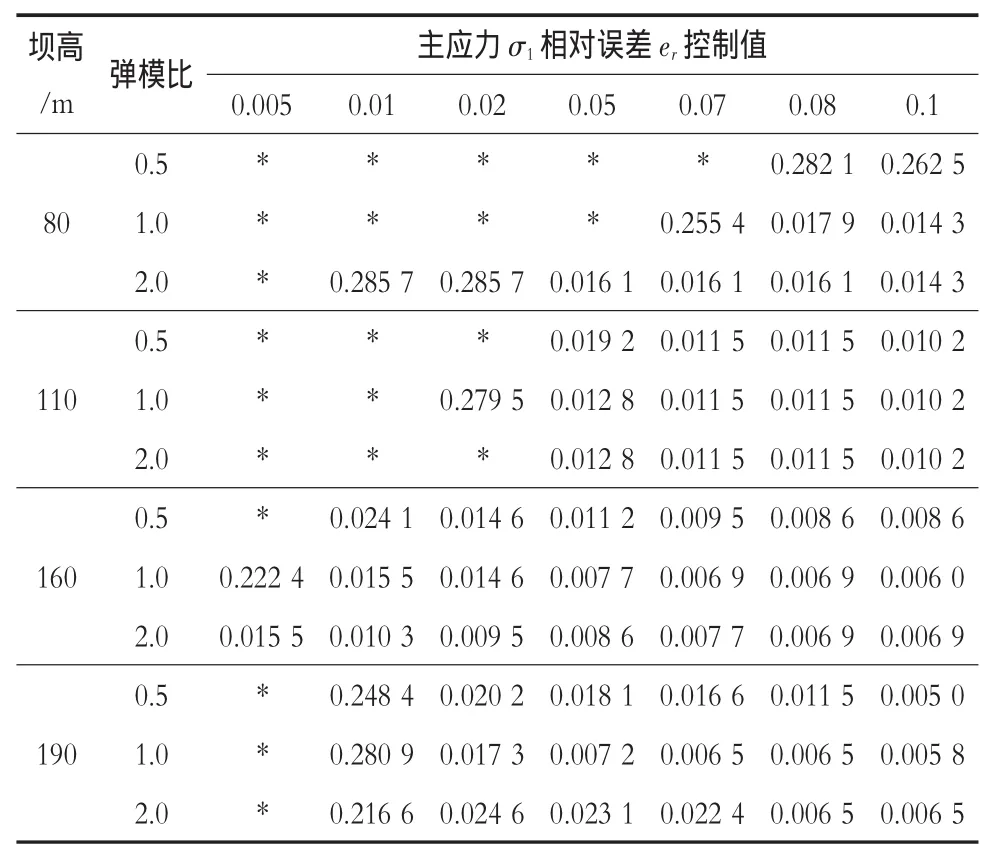
表312種工況，7種主應力σ1的相對誤差控制值計算得出的壩踵沿建基面的相對寬度

3）局部條件下的應力控制標準。通過以上2點的分析，得出一些局部壩體的定量標準：在地基與壩體彈模比較小、壩高較小的情況下，網格剖分的不同對壩踵的主應力σ1的大小和分布影響越大，很難確定壩踵的應力控制標準。對于地基與壩體模比大于1.0、壩高大于80的壩體。其可以采用不同網格之間的5%的主應力σ1的相對誤差作為控制標準，此時，應力失真區沿建基面的相對寬度可以認為小于2%。

5 結語

由于影響壩體的影響因素、計算工況很多，所以計算量很大。本文是基于平面四邊形單元、考慮部分影響因素探討了重力壩壩踵區的應力控制標準，成果的整理和分析相對比較粗糙，關于重力壩有限元的強度控制標準，還需要做大量后續工作。

［1］王春濤，練繼建.重力壩壩踵應力集中問題的有限元法研究［J］.水利水電技術，2003（5）：10-12.

［2］趙代深.重力壩有限元計算網格剖分與應力控制標準問題［J］.水利學報，1996（5）：37-43.