變值配置函數(shù)空間整體編碼族的2維對(duì)稱性

鄭智捷

(云南大學(xué)軟件學(xué)院信息安全系,云南昆明650091)

在0-1域中,利用邏輯變量和函數(shù)模型進(jìn)行開(kāi)關(guān)代數(shù)分析、設(shè)計(jì)、描述、優(yōu)化,以及超大規(guī)模集成電路設(shè)計(jì)和邏輯門陣列實(shí)現(xiàn),通過(guò)卡諾圖,合取范式,析取范式等方法獲得邏輯函數(shù)表示[1-4]已有一系列的規(guī)范標(biāo)準(zhǔn)[1-8]。這類數(shù)理邏輯工具為現(xiàn)代信息和知識(shí)產(chǎn)業(yè)建立起堅(jiān)實(shí)基礎(chǔ),為先進(jìn)的電腦和網(wǎng)絡(luò)技術(shù)大規(guī)模普及發(fā)展做出了實(shí)質(zhì)貢獻(xiàn)[1-13]。從形式化邏輯發(fā)展的角度,0-1邏輯體系奠定的數(shù)理邏輯基礎(chǔ)[1-6],推動(dòng)了當(dāng)今世界先進(jìn)科學(xué)技術(shù)發(fā)展的輝煌成就[1-13]。

在復(fù)雜性科學(xué)[16-20]中元胞自動(dòng)機(jī)模型[16-23]利用邏輯函數(shù)遞歸處理方法,對(duì)動(dòng)態(tài)圖像變化模式進(jìn)行深入探討。在Wolfram開(kāi)創(chuàng)的“新一代科學(xué)”系列研究[24-26]中,除了按照順序編號(hào)觀察遞歸函數(shù)的復(fù)雜動(dòng)態(tài)特性之外,研究焦點(diǎn)在探尋單個(gè)函數(shù)反復(fù)迭代操作下可能出現(xiàn)的不同圖像變化輸出模式[16-27]。

離散邏輯函數(shù)空間的隨機(jī)組合帶來(lái)非規(guī)范特性,不同的表示結(jié)構(gòu)對(duì)應(yīng)的變換空間具有內(nèi)蘊(yùn)的非數(shù)值化特征和巨大組合數(shù)目。對(duì)整體邏輯配置函數(shù)空間進(jìn)行研究是一類高難度系統(tǒng)探索性問(wèn)題[16-21,28-32]。

由于缺乏合適的基本原理、模型方法和輔助工具,整體化變換群結(jié)構(gòu)和組織的特性有待于深入研究。利用文獻(xiàn)[40-44]中對(duì)規(guī)則化平面格黑白圖像基礎(chǔ)和應(yīng)用研究,提出基本的組織原理和方法。利用多變量0-1序列,從整體編碼角度針對(duì)變值體系結(jié)構(gòu)等價(jià)性和對(duì)稱性方面進(jìn)行分析[38-39]。

利用廣義和文王等編碼系列,形成高維系統(tǒng)分析工具框架,對(duì)多變量函數(shù)群集提供展示環(huán)境。

論文第一章給出基礎(chǔ)定義和變值基元的不變特征,第二章對(duì)n元邏輯變量建立配置函數(shù)空間,引入兩類擴(kuò)展算符：向量化置換運(yùn)算和互補(bǔ)運(yùn)算模式。定義了廣義編碼結(jié)構(gòu)和2維編碼表示系列。在第三章和第四章中,應(yīng)用基元向量結(jié)構(gòu)和變值編碼系列,對(duì)單個(gè)和兩個(gè)0-1變量的邏輯函數(shù)空間進(jìn)行展示;在第五章中總結(jié)所建立的模型和方法。

1 基本定義

1.1 N元0-1序列

令 x=xn-1…xi…x0,0≤i＜n為n元 0-1變量,記 k為指定的關(guān)聯(lián)位置0≤k＜n,輸出變量y,n變量函數(shù)f,y=f(x),xi,y∈B2={0,1},x∈B={0,1}n

例如：X=01101110,Y=11000111為長(zhǎng)度為 N=8的1維0-1序列。最右側(cè)為第0位,最左側(cè)為第7位。

1.2 在邏輯變換中的變值特性

令n元變量序列中的第k個(gè)位置為關(guān)聯(lián)位置,在N元序列中,該位置為當(dāng)前位j,所選定的位置在后繼處理中有特殊重要性。

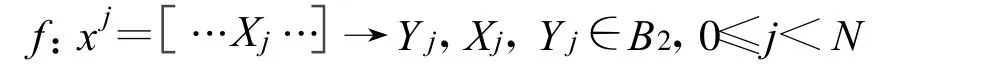
對(duì)任意的邏輯變量,在選定了函數(shù)之后關(guān)聯(lián)位置形成Xj→Yj點(diǎn)-點(diǎn)對(duì)應(yīng)位置關(guān)系。即該模式由當(dāng)前輸入狀態(tài)和函數(shù)輸出狀態(tài)之間建立的關(guān)系。

由于關(guān)聯(lián)位置1-1對(duì)應(yīng)取值為 0-1,輸入/輸出值共有 4類基元變化模式：A：0→0,B：0→1,C：1→0,D：1→1 4類模式,利用變值基元可以建立起更為靈活的表達(dá)方式。

例如：邏輯代數(shù)的標(biāo)準(zhǔn)范式最大項(xiàng)(1點(diǎn)：B和D類)和最小項(xiàng)(0點(diǎn)：A和C類)傳統(tǒng)邏輯析取及合取范式函數(shù)是通過(guò)選擇最大項(xiàng)(1點(diǎn))或者最小項(xiàng)(0點(diǎn))集合來(lái)決定[1-6],4類變值基元模式以更為豐富的表達(dá)形式構(gòu)成函數(shù)方程。

從元胞自動(dòng)機(jī)的角度,當(dāng)前的輸入狀態(tài)和輸出狀態(tài)是相互關(guān)聯(lián)的。該類關(guān)系決定變化基元本身在函數(shù)空間中的內(nèi)蘊(yùn)特性。

在4類變值模式中,第B和C類對(duì)應(yīng)變值群集;而A和D類對(duì)應(yīng)不變值群集。

2 n元變量狀態(tài)空間和配置函數(shù)空間

N長(zhǎng)0-1序列在環(huán)轉(zhuǎn)連接下,利用給定位置k的n元變量模式進(jìn)行操作。

2.1 n元變量和基元狀態(tài)

令N長(zhǎng)0-1序列為環(huán)狀結(jié)構(gòu),以忽略序列邊界效應(yīng),對(duì)任意的整數(shù) n,k;0≤k＜n,0＜n≤N,n為變量數(shù)目,k為關(guān)聯(lián)點(diǎn)距離最右位的偏移量。隨著關(guān)聯(lián)點(diǎn)位置的變動(dòng),n元變量在環(huán)上對(duì)應(yīng)移動(dòng)。

輸入輸出變量的關(guān)聯(lián)狀態(tài)：

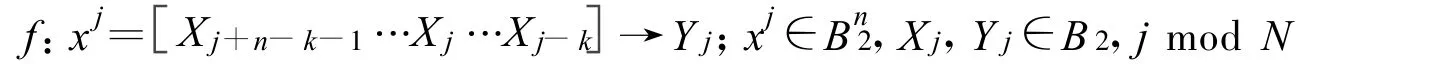
n個(gè)輸入變量形成一個(gè)狀態(tài),每個(gè)變量取值為0-1,共有2n個(gè)狀態(tài)形成狀態(tài)空間。

可區(qū)分的狀態(tài)空間在表1中示意。

表1 基元向量及其狀態(tài)編號(hào)

n變?cè)?dú)立取值,共有2n可區(qū)分狀態(tài),每個(gè)狀態(tài)編號(hào) I數(shù)值的0-1取值對(duì)應(yīng)著一個(gè)給定的n元狀態(tài)向量。第I個(gè)基元向量,在系統(tǒng)中2n基元向量形成基元向量空間。

函數(shù)空間及表示向量

記J=J2n-1…Jj…J0,0≤j＜2n,Jj∈B2,為長(zhǎng)度為2n位的函數(shù)向量,每個(gè)函數(shù)向量 J確定一個(gè)邏輯函數(shù),共有向量構(gòu)成函數(shù)空間在表2中示意。

表2 函數(shù)向量及其函數(shù)編號(hào)

2.2 順序編碼-邵雍-Leibniz編碼

在公元11世紀(jì),邵雍首先提出按二叉樹(shù)形成的順序排列黑白圖像表示方法[33-37]。在公元17世紀(jì),Leibniz使用0-1序列將樹(shù)狀黑白圖像模式表示成二進(jìn)制算術(shù)表示[15,32]。

定義2.2.1：邵雍-Leibniz編碼(SL碼)為函數(shù)表中按二進(jìn)制編號(hào)順序排列的序列

證明：按照二進(jìn)制計(jì)數(shù)的模式,在每個(gè)編號(hào)向量中1值對(duì)應(yīng)最大項(xiàng),0值對(duì)應(yīng)最小項(xiàng)。所選擇的編號(hào)值集合和函數(shù)形成1-1對(duì)應(yīng)關(guān)系。

2.3 1維編碼-廣義編碼和配置函數(shù)空間

記Ωm為m元對(duì)稱置換群結(jié)構(gòu)。

令P為置換算符,

定理2.3.1：在置換算符P的作用下,所有的可區(qū)分的2n!置換函數(shù)向量組成一個(gè)邏輯函數(shù)向量置換群空間。

證明：置換算符作用在特征向量上,向量共有2n不同位置,第0個(gè)位置有2n種選擇,…,第 j位置有2n-j種選擇,…,第2n-2位置有2種選擇,第2n-1位置僅有1種選擇方式。可能的總數(shù)目為各個(gè)位置選擇數(shù)目的乘積。

對(duì)每個(gè)基元向量的位置可以選擇原來(lái)的值,或者為相反的值。定義互補(bǔ)運(yùn)算Q,在向量的模式下,令Q為一個(gè)2n長(zhǎng)0-1向量,P(J)Q=P(J2n-1)Q2n-1…P(Jj)Qj…P(J0)Q0

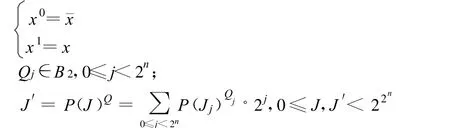
為方便描述,在P和Q兩類算符作用下形成的空間稱為配置函數(shù)空間,一個(gè)選定的P和Q算符確定一個(gè)配置函數(shù),每個(gè)配置函數(shù)包含按廣義編碼排列的個(gè)函數(shù)。

定義2.3.2：廣義編碼(G碼)是由P和Q算符對(duì)2n位長(zhǎng)向量J作用后,形成的配置編碼模式。

定理2.3.3：在P和Q兩類算符作用下,廣義編碼P(J)Q所包含的可區(qū)分配置函數(shù)數(shù)目為

證明：對(duì)每個(gè)互補(bǔ)運(yùn)算j,Qj有兩種選擇,Q的選擇總數(shù)為;對(duì)置換算符基元向量在P算符的作用下形成2n!置換群,總數(shù)目為二者的乘積。

廣義編碼配置函數(shù)的數(shù)目為n元邏輯互補(bǔ)空間的算符數(shù)目與2n個(gè)基元置換對(duì)稱群算符數(shù)目的乘積。

2.4 二維編碼

廣義編碼,在P,Q變換下所形成的編號(hào)還是22n向量的一個(gè)置換,在配置函數(shù)變換空間中存在置換,將其重排為與SL編碼對(duì)應(yīng)的順序編號(hào)模式。

為方便地描述2維結(jié)構(gòu),

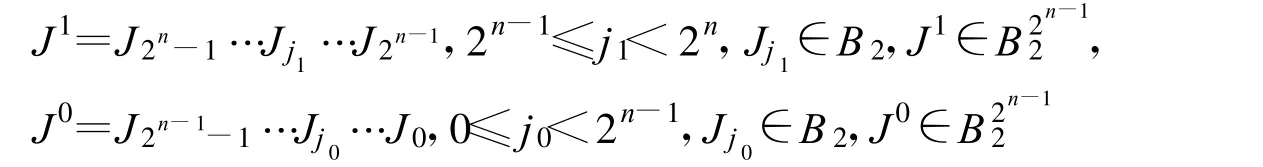
令P(J)Q=P〈J1|J0〉Q形成二維編碼。

公元前13世紀(jì),周文王(姬昌)首先引入了非對(duì)稱排列,將八卦圖示表示為兩個(gè)置換群集[33-37]。用文王命名這類形成二維表示的編碼結(jié)構(gòu)。

定義2.4.1：文王碼(W 碼)為滿足 P(J)Q=P〈J1|J0〉Q條件,形成的通用型二維編碼。

定理2.4.2：文王編碼等價(jià)于廣義編碼,文王編碼提供一個(gè)2維平面框架顯示選定的配置函數(shù)中各個(gè)函數(shù)的相對(duì)位置。

證明：每個(gè)廣義編碼的編號(hào)能寫為〈J1|J0〉文王編碼的標(biāo)準(zhǔn)形式,在表3中每個(gè)邏輯函數(shù)在配置函數(shù)表示空間中有一個(gè)確定的位置,

表3 2維展示框架

通過(guò)文王碼的兩個(gè)子編號(hào),將函數(shù)集展示在2維平面上。

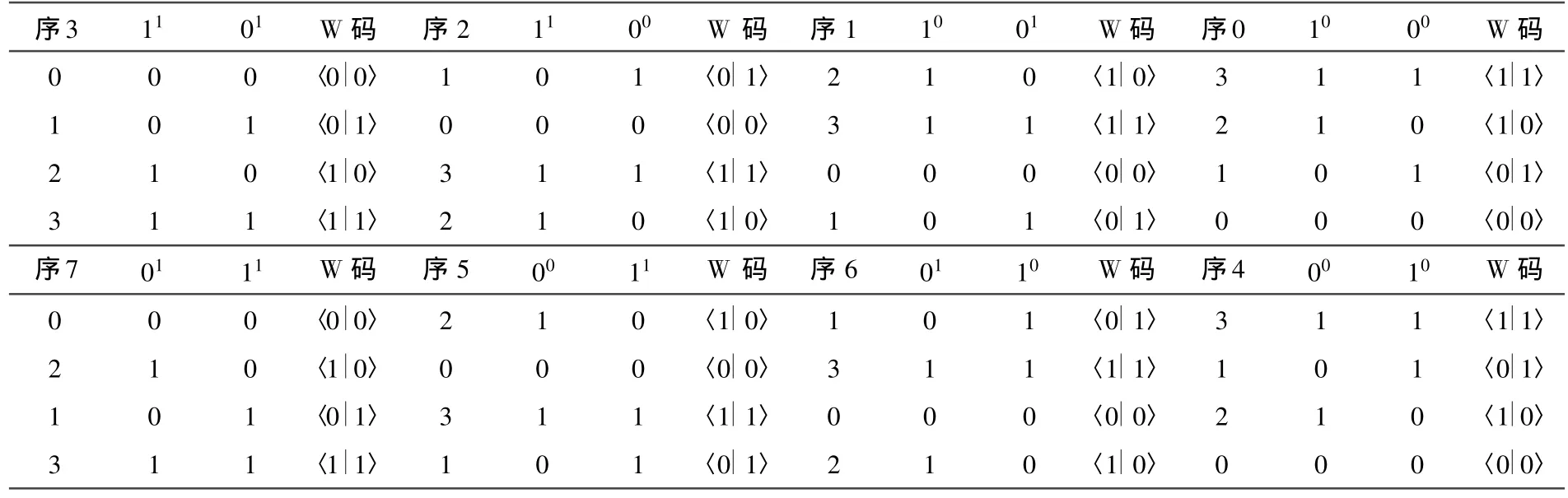
表4 n=1廣義編碼和文王編碼序列

二維廣義編碼排列為：

如何才能激發(fā)學(xué)生學(xué)習(xí)的愿望，教師在設(shè)計(jì)練習(xí)時(shí)要充分考慮兒童的心理特點(diǎn)，教師結(jié)合學(xué)生已有知識(shí)盡量使練習(xí)設(shè)計(jì)新穎，生動(dòng)有趣，只有有趣的練習(xí)，才能調(diào)動(dòng)學(xué)生做練習(xí)的積極性。

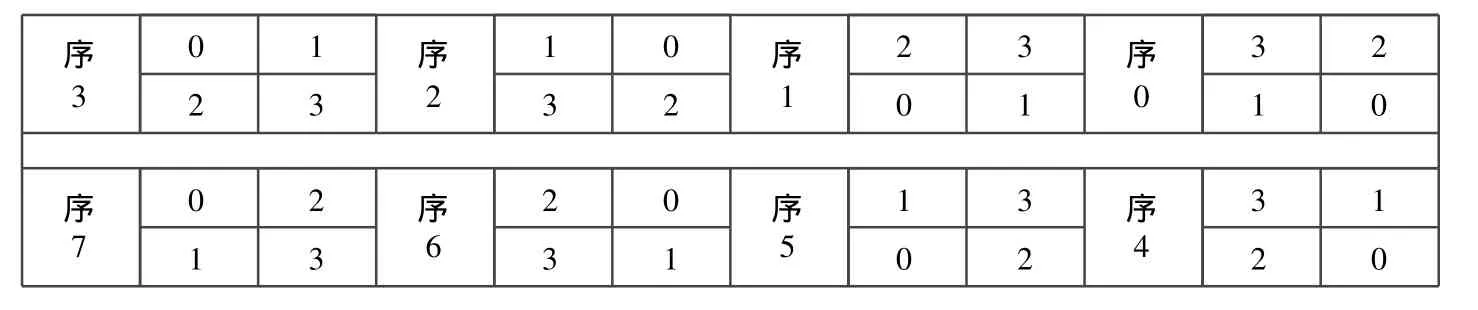
序3 0 1 1 0序2 2 3序1 3 2序0 2 3 3 2 0 1 1 0序7 0 2 2 0序6 1 3序5 3 1序4 1 3 3 1 0 2 2 0

8個(gè)二維表不同函數(shù)排列：

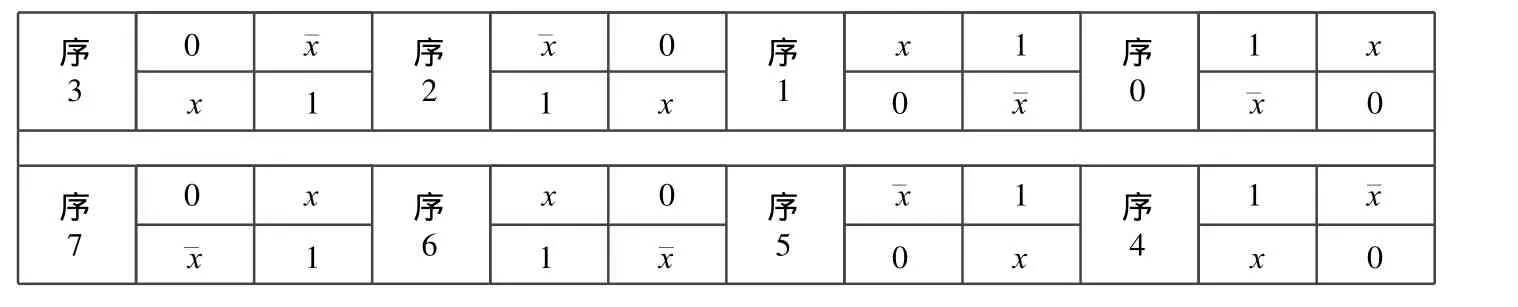
序3 0 ˉxˉx 0序2 x 1序1 1 x序0 x 1 1 x 0 ˉxˉx 0序7 0 x x 0序6ˉx 1序5 1 ˉx序4ˉx 1 1 ˉx 0 x x 0

置換和互補(bǔ)運(yùn)算不會(huì)改變函數(shù)本身,但將不同的配置函數(shù)排列成可區(qū)分的結(jié)構(gòu)。這樣不變特性為整體分析提供分析比較圖式。

2.5 伏羲編碼和共軛編碼

公元前45世紀(jì),伏羲排出對(duì)稱編排的八卦模式[33-37],用伏羲命名這類配對(duì)的對(duì)稱編碼。

定義2.5.1：對(duì)2維文王編碼,如果?j1-2n-1=j0,0≤j0＜2n-1,2n-1≤j1＜2n同時(shí)Ij1=ˉIj0,即兩個(gè)相差2n-1的基元按照配對(duì)的模式排列互為互補(bǔ)向量表示,則該類編碼為伏羲編碼(F碼),也稱為廣義共軛編碼(GC碼)。

如果還有更強(qiáng)地約束基元配對(duì),則形成另一類編碼。

定義2.5.2：在伏羲編碼系列中,如果對(duì)?Ij0∈IJ0,對(duì)基元特定的位置i,,(或者?Ii=1),0≤i＜2n-1,則該類編碼為共軛編碼(C碼)。

在配對(duì)條件下的兩種編碼有如下定理。

定理2.5.4：對(duì)n元變量結(jié)構(gòu),C碼的數(shù)目是8×(2n-1)!

證明：基元向量互補(bǔ)算符Q共有4種可能性。由于置換算符P前一半的基元同后一半的基元有配對(duì)要求,同時(shí)對(duì)基元特定的位置i,?Ii∈Ij0&Ii=0,(或者?Ii=1)0≤i＜n,一共有!組合。兩類算符相互獨(dú)立,編碼總數(shù)為兩者數(shù)目的乘積。

2.6 幾種編碼方案比較

為了比較不同的編碼系列,在表5中列出主要編碼和計(jì)算公式。以判斷編碼的整體特性。

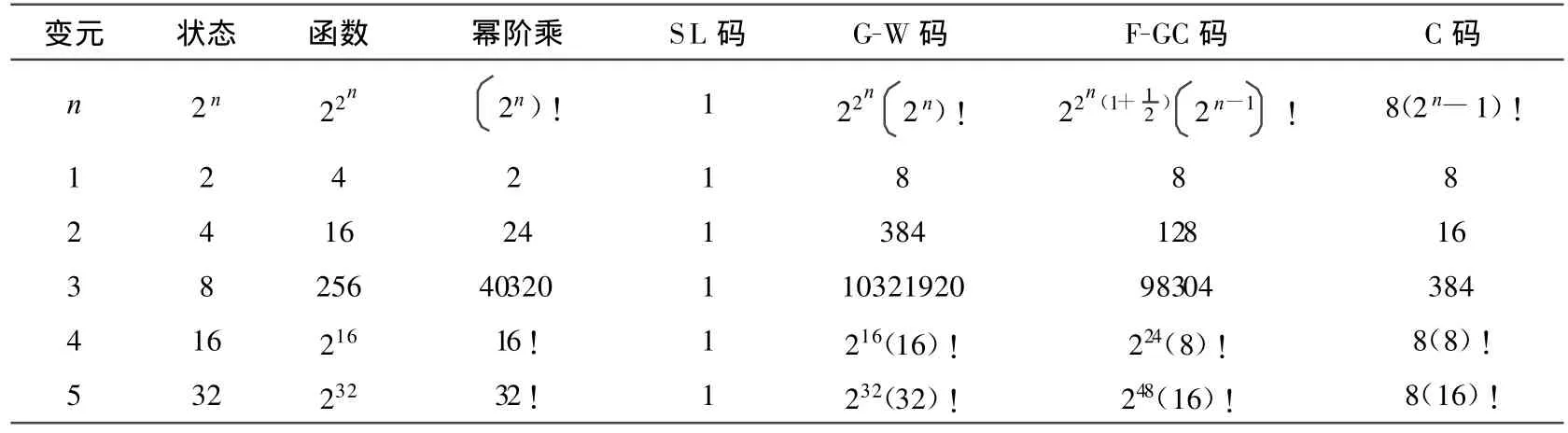
表5 不同編碼計(jì)算公式比較

在單個(gè)變?cè)臈l件下,8個(gè)G-W碼序列也是F-GC碼和C碼序列。

隨著變?cè)獢?shù)目超幾何級(jí)數(shù)增長(zhǎng),詳細(xì)研究只可能針個(gè)例,不能進(jìn)行窮舉性遍歷。

在下面的章節(jié)中,研究單變量和雙變量的配置函數(shù)空間展示分布情況。

3 單變量和雙變量的表示結(jié)構(gòu)

3.1 基本模式

對(duì)單變量函數(shù),

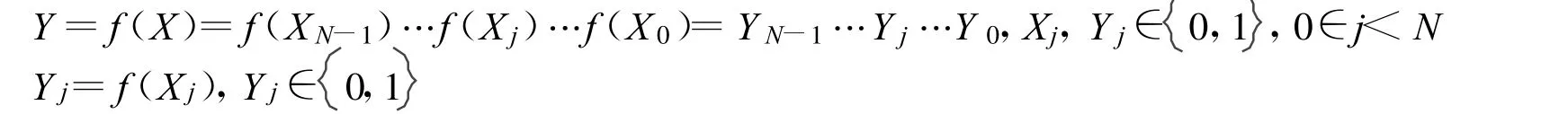
單元函數(shù)為1-1變換關(guān)系,按照公式

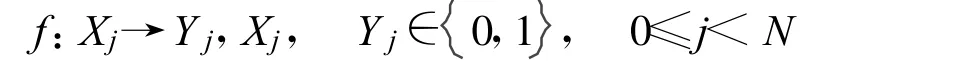
對(duì)輸入變量在輸入向量上求值,得到函數(shù)的輸出序列。

對(duì)雙變量函數(shù),將首尾銜接成環(huán)狀,由于變換的非對(duì)稱性有兩種變換模式：

類型A：

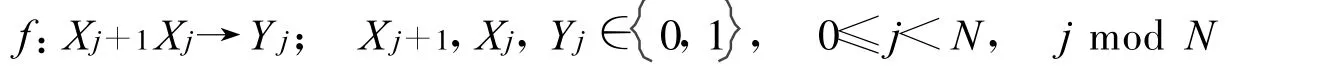
或者

類型B：

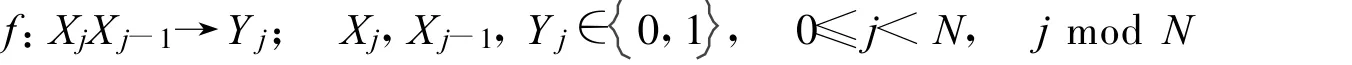
或者

3.2 單變量配置函數(shù)空間

從邏輯代數(shù)的角度,單變量函數(shù)是最基本的函數(shù)。函數(shù)空間表示如下：令 x為邏輯變量x∈{0,1}

在一元邏輯函數(shù)空間中有4個(gè)函數(shù),編號(hào)為0-3。在單變量下,各類編碼都是相同的,考察SL碼和C碼的編號(hào)排列。

3.3 單變量函數(shù)的SL編碼和C編碼表示

對(duì)單變量函數(shù),用如下的規(guī)則構(gòu)造其表示空間：

(1)將狀態(tài)空間分為兩個(gè)集合：0,1;

(2)按照選擇及不選擇,在函數(shù)空間中建立關(guān)系;

(3)在狀態(tài)集合1,0上,互補(bǔ)10,01集合在〈J1|J0〉模式中標(biāo)記為編號(hào);

(4)記 f(〈J1|J0〉|x)的基本結(jié)構(gòu)〈J1|J0〉為選擇的變值函數(shù)表示：

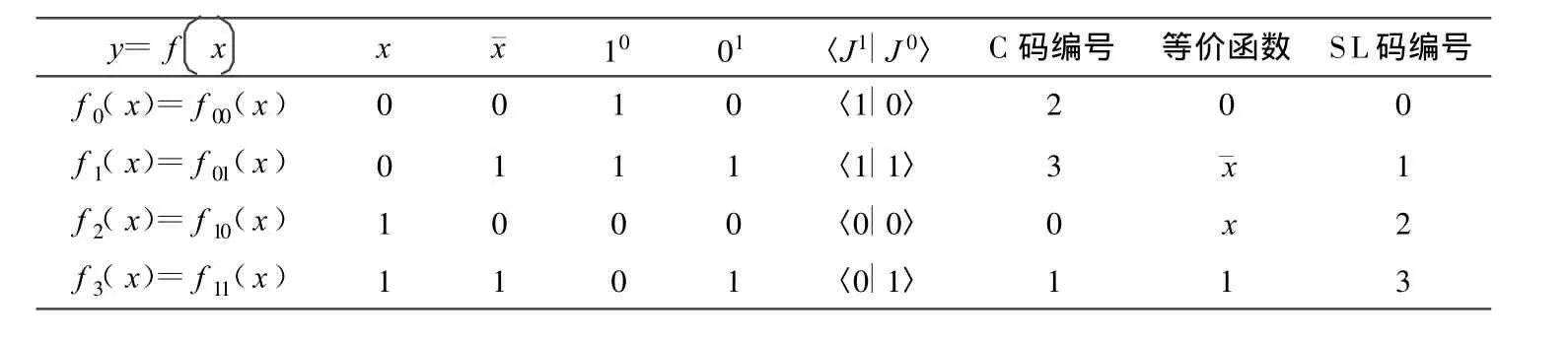
y=f x x ˉx 10 01 〈J1|J0〉 C碼編號(hào) 等價(jià)函數(shù) SL碼編號(hào)f0(x)=f00(x)0 0 1 0 〈1|0〉 2 0 0 f1(x)=f01(x)0 1 1 1 〈1|1〉 3 ˉx 1 f2(x)=f10(x)1 0 0 0 〈0|0〉 0 x 2 f3(x)=f11(x)1 1 0 1 〈0|1〉 1 1 3

其他函數(shù)的等價(jià)特性關(guān)系,亦能通過(guò)選擇集合驗(yàn)證。

3.4 共軛表示的定理和推論

從3.3節(jié)中可以看到,利用最大項(xiàng)或者最小項(xiàng)組合所構(gòu)成的函數(shù),與通過(guò)變值基元構(gòu)成的函數(shù)是相互等價(jià)的。兩個(gè)配置函數(shù)空間具有同樣的大小,不同的編號(hào)和函數(shù)可以相互比較。

從基元變換群的角度,基元狀態(tài)形成變值基元。這樣的描述特征有利于克服經(jīng)典系統(tǒng)適合表達(dá)靜態(tài)組合特性而缺乏動(dòng)態(tài)描述功能的局限。

利用對(duì)應(yīng)關(guān)系,得到等價(jià)性定理。

定理3.4.1：?jiǎn)巫兞窟壿嫼瘮?shù)空間和單變量變值函數(shù)空間的可區(qū)分函數(shù)總數(shù)為221=4。在兩個(gè)結(jié)構(gòu)中的4個(gè)函數(shù)1-1對(duì)應(yīng)。

證明：利用4個(gè)函數(shù)的對(duì)應(yīng)關(guān)系,等價(jià)性成立。

在結(jié)構(gòu)中形成的4個(gè)頂點(diǎn)有明確地意義。

推論3.4.2：在變值表示中,4個(gè)函數(shù)有如下的變換意義,

(1)f(〈0|1〉|x)保持{1}點(diǎn)狀態(tài)不變,轉(zhuǎn)化{0}點(diǎn)為1。對(duì)應(yīng)邏輯代數(shù)的1函數(shù);

(2)f(〈0|0〉|x)保持原有的值不變。對(duì)應(yīng)原函數(shù) x;

(3)f(〈1|1〉|x)將{0}點(diǎn)轉(zhuǎn)化為1值,同時(shí)將{1}點(diǎn)轉(zhuǎn)化為0值。對(duì)應(yīng)邏輯代數(shù)的非函數(shù)ˉx;

(4)f(〈1|0〉|x)保持{0}點(diǎn)狀態(tài)不變,轉(zhuǎn)化{1}點(diǎn)為0值。對(duì)應(yīng)0值函數(shù)。

證明：對(duì)1元邏輯函數(shù),只有上述4種情況。

推論3.4.3：1元函數(shù)的函數(shù)空間同變值函數(shù)空間同構(gòu)。

證明：在兩個(gè)結(jié)構(gòu)中任意函數(shù)明確的1-1對(duì)應(yīng)。

應(yīng)用例子

對(duì)給定的0-1序列 X=01101110,8位長(zhǎng)的二進(jìn)制序列,1元共軛函數(shù)空間生成如下4種輸出序列：

4 雙變量的表示結(jié)構(gòu)

對(duì)任意n變量,狀態(tài)數(shù)目為2n,函數(shù)空間數(shù)目為。在雙變量函數(shù)空間中共有16個(gè)函數(shù)。

4.1 A型雙變量表示

對(duì)A型模式,序列X,下列關(guān)系成立：

f x 0 1 z 0 1

雙變量 x,z一共有4種狀態(tài)組合：

16個(gè)函數(shù)的不同編碼在表6中示意。

對(duì)雙變量函數(shù),用如下的規(guī)則表示：

(1)將zx的狀態(tài)空間根據(jù)x點(diǎn)取值為0或者1分為兩個(gè)集合：{0,2},{3,1};

(2)狀態(tài)集0：3;2：1是共軛對(duì);

(3)由1(0)點(diǎn)狀態(tài)決定J1(J0)的集合;

(4)選擇狀態(tài)為1,不選擇為0,建立對(duì)應(yīng)關(guān)系;

(5)〈J1|J0〉為變值表示：f(〈J1|J0〉|zx)

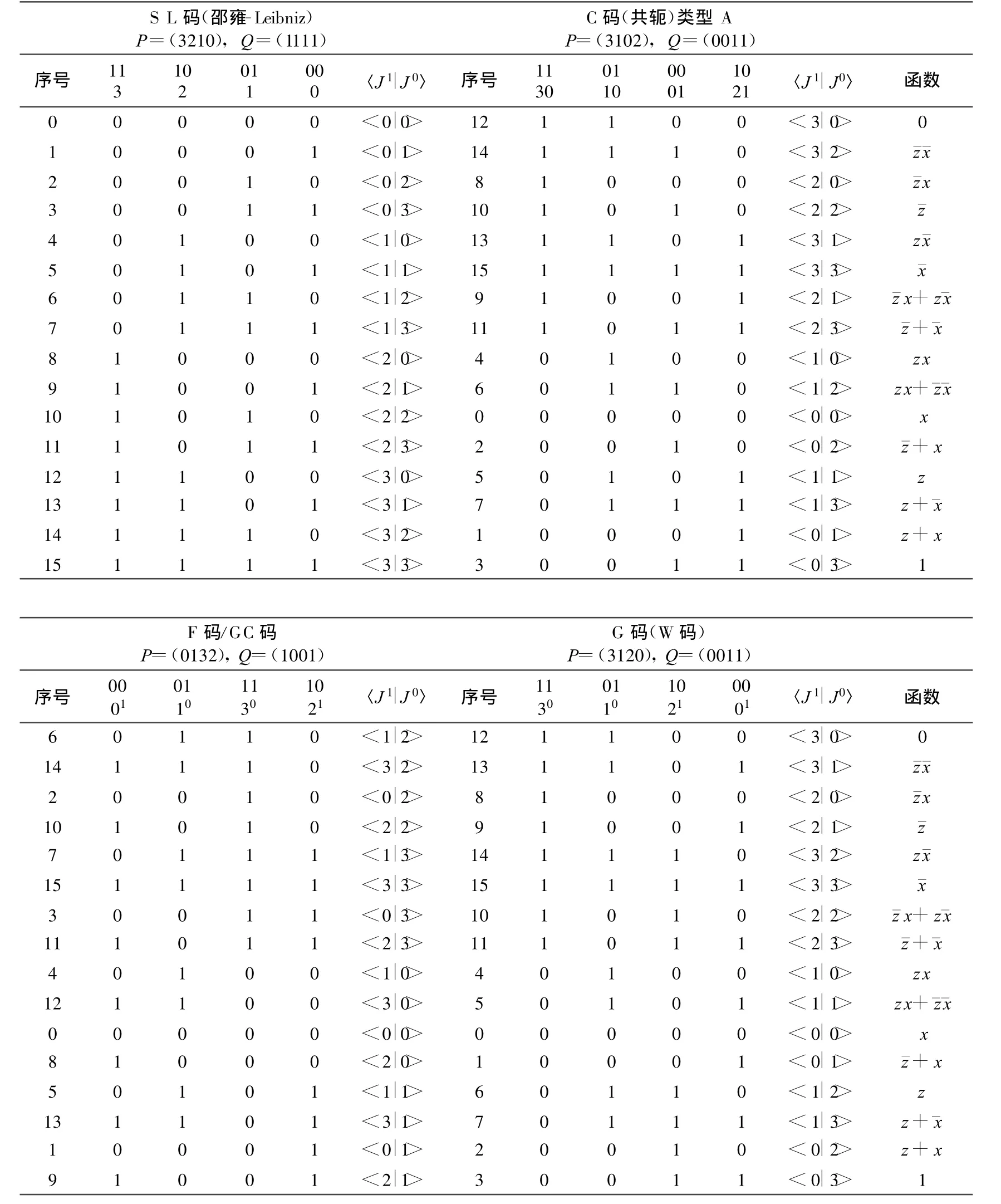
表6 1維排列SL C(類型A),F,G,W 各類表示

二維展示：

SL碼順序排列 SL碼函數(shù)分布

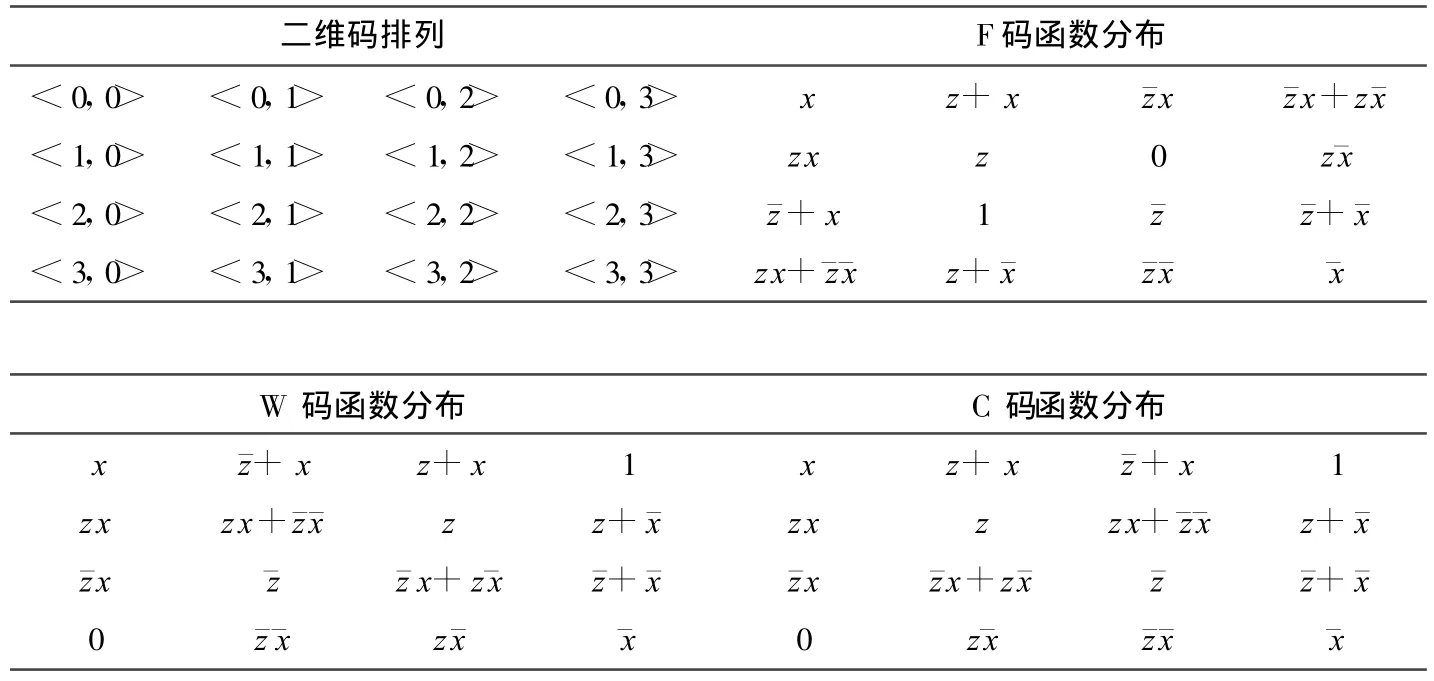
二維碼排列 F碼函數(shù)分布＜0,0＞ ＜0,1＞ ＜0,2＞ ＜0,3＞ x z+x ˉzx ˉzx+zˉx＜1,0＞ ＜1,1＞ ＜1,2＞ ＜1,3＞ zx z 0 zˉx＜2,0＞ ＜2,1＞ ＜2,2＞ ＜2,3＞ ˉz+x 1 ˉz ˉz+ˉx＜3,0＞ ＜3,1＞ ＜3,2＞ ＜3,3＞ zx+ˉzˉx z+ˉx ˉzˉx ˉx W碼函數(shù)分布 C碼函數(shù)分布x ˉz+x z+x 1 x z+x ˉz+x 1 zx zx+ˉzˉx z z+ˉx zx z zx+ˉzˉx z+ˉxˉzx ˉz ˉz x+zˉx ˉz+ˉx ˉzx ˉzx+zˉx ˉz ˉz+ˉx 0ˉzˉx zˉx ˉx 0 zˉx ˉzˉx ˉx

將得到的結(jié)果,總結(jié)為定理形式。

定理4.1.1：對(duì)多元變量等價(jià)變值函數(shù)集表示,SL編碼不同于C編碼的排列模式。

證明：觀察SL碼的基元向量,當(dāng)變?cè)獢?shù)目大于1時(shí)。按順序排列的前一半和后一半向量通常不會(huì)滿足廣義共軛條件。

定理4.1.2：對(duì)任意的F編碼,按主對(duì)角線劃分,對(duì)應(yīng)編號(hào)的函數(shù)為成對(duì)共軛函數(shù)。

證明：在F編碼條件下,任意選擇的編號(hào)〈J1|J0〉其在對(duì)角線另一側(cè)的編號(hào)是〈J0|J1〉。該編號(hào)是原向量集的共軛變量集合。

觀察上面例子中的F碼和C碼的函數(shù)分布,函數(shù)對(duì)滿足成對(duì)共軛關(guān)系。

定理4.1.3：對(duì)任意的C編碼,除了主對(duì)角線的共軛對(duì)稱性之外,4個(gè)頂點(diǎn)為：0,x,ˉx,1

證明：在上述4種情況中,x什么都不變自然保持輸入變?cè)瓲顟B(tài)直接輸出;1函數(shù)將0點(diǎn)變?yōu)?,輸出1向量;0函數(shù)轉(zhuǎn)化1點(diǎn)為0,輸出0向量;ˉx把0點(diǎn)變?yōu)?,同時(shí) 1點(diǎn)變?yōu)?,輸出為原值求反。

4頂點(diǎn)不變性是C類編碼特有的空間結(jié)構(gòu)特征。

定理4.1.4：在文王編碼中如果基元向量集無(wú)成對(duì)匹配,則其對(duì)應(yīng)函數(shù)分布一般不出現(xiàn)共軛對(duì)稱效應(yīng)。

證明：由于編碼規(guī)則的約束,非成對(duì)匹配形成非對(duì)稱排列。但可能在一些團(tuán)體組合模式下以個(gè)例顯現(xiàn)共軛對(duì)稱性,定理的結(jié)論對(duì)大部分情況能夠成立。

觀察前面G碼的例子,盡管大多數(shù)函數(shù)對(duì)非共軛對(duì)稱,但是兩個(gè)頂點(diǎn)函數(shù)(0和1)仍保持共軛對(duì)稱。

5 結(jié)論

對(duì)多變量條件下利用傳統(tǒng)東方邏輯結(jié)構(gòu)建立起現(xiàn)代化變值邏輯變換體系。利用變值基元向量,建立了整體編碼模型和系列化編碼展示結(jié)構(gòu)。

定理4.1.1-4.1.4總結(jié)論文的主要結(jié)果。在新的編碼系列中,文王編碼具有通用二維結(jié)構(gòu)。伏羲編碼在配置函數(shù)空間中形成共軛函數(shù)對(duì)。而共軛編碼,特有的四元極值頂點(diǎn)將其他的編號(hào)約束在內(nèi)。

由于文王編碼系列具有超幾何級(jí)數(shù)增長(zhǎng)的趨式,下一步的工作將集中在對(duì)較少量變?cè)?2-4)的變換結(jié)構(gòu)進(jìn)行實(shí)際的模擬處理和窮舉型計(jì)算。同時(shí)應(yīng)用該理論體系處理數(shù)學(xué)/物理的基礎(chǔ)悖論問(wèn)題,為實(shí)際應(yīng)用現(xiàn)代東方邏輯系統(tǒng)：變值邏輯體系開(kāi)辟道路。

致謝：感謝已故的恩師高慶獅院士,高先生早在30年前就指導(dǎo)作者在對(duì)稱置換群上構(gòu)造并行算法。感謝陳濤先生利用分層結(jié)構(gòu)化模型建立的現(xiàn)代中醫(yī)輔助診斷系統(tǒng),應(yīng)用傳統(tǒng)中醫(yī)理論形成現(xiàn)代化成果激勵(lì)作者重返基礎(chǔ)邏輯研究前沿。感謝云南省特色專業(yè)建設(shè)基金和云南省軟件工程重點(diǎn)實(shí)驗(yàn)室信息安全專項(xiàng)基金支持。

[1]楊炳儒.布爾代數(shù)及其泛化結(jié)構(gòu)[M].北京：科學(xué)出版社,2008.

[2]S P Vingron.Switching Theory：Insight Through Predicate Logic[M].Springer,2004.

[3]秦軍南.開(kāi)關(guān)理論與邏輯設(shè)計(jì)[M].北京：人民教育出版社,1980.

[4]Saburo Muroga.Logic Design and Switching Theory[M].Wiley-Interscience Publication,1979.

[5]A Kandel,Samuel C Lee.Fuzzy Switching and Automata：Theory and Applications[M].Crane Russak&Company Inc,1979.

[6]Samuel C Lee.Modern Switching Theory and Digital Design[M].Prentice-Hall Inc,1978.

[7]F H Edwards.The Principles of Switching Circuits[M].MIT Press,1973.

[8]霍書(shū)全.多值邏輯的方法和理論[M].北京：科學(xué)出版社,2009.

[9]石純一.數(shù)理邏輯與集合論(第二版)[M].北京：清華大學(xué)出版社,2000.

[10]胡世華,陸鐘萬(wàn).數(shù)理邏輯基礎(chǔ)[M].北京：科學(xué)出版社,1981.

[11]金岳霖.形式邏輯[M].北京：人民出版社,1979.

[12]數(shù)理邏輯論文選：第一集,1958.

[13]A B Rosser,A R Turquette.Many-valued Logics[M].North-Holland Publishing Company,1952.

[14]桑靖宇.萊布尼茲與現(xiàn)象學(xué)[M].北京：中國(guó)社會(huì)科學(xué)出版社,2009.

[15]閻莉.整體論視域中的科學(xué)模型觀[M].北京：科學(xué)出版社,2008.

[16]雷功炎.數(shù)學(xué)模型八講[M].北京：北京大學(xué)出版社,2008.

[17]宣慧玉,張發(fā).復(fù)雜系統(tǒng)仿真及其應(yīng)用[M].北京：清華大學(xué)出版社,2008.

[18]李士勇.非線性科學(xué)與復(fù)雜性科學(xué)[M].哈爾濱：哈爾濱工業(yè)大學(xué)出版社,2006.

[19]涂序彥,尹怡欣.人工生命及應(yīng)用[M].北京：北京郵電大學(xué)出版社,2004.

[20]H Umeo,S Morishita,K Nishinari.Cellular Automata[M].Springer,2008.

[21]江志松.122號(hào)初等元胞自動(dòng)機(jī)的復(fù)雜性分析[J].科學(xué)通報(bào),2000,45(18)：2007-2012.

[22]D Griffeath,C Moor.New Constructions in Cellular Automata[C].Santa Fe Institute Studies in the Sciences of Complexity,2003.

[23]A Ilachinski.Cellular Automata-A Discrete Universe[M].World Scientific,2001.

[24]S Wolfram.A New Kind of Science[EB/OL].http：//www.wolframscience.com,2002.

[25]S Wolfram.Cellular Automata and Complexity.Addison-Wesley,1994.

[26]S Wolfram.Theory and Applications of Cellular Automata.World Scientific,1986.

[27]李元香.格子氣體自動(dòng)機(jī)[M].北京：清華大學(xué)出版社,1994.

[28]金日光.模糊群子論[M].哈爾濱：黑龍江科學(xué)技術(shù)出版社,1985.

[29]Wiktor Marek etc.Elements of Logic and Foundations of Mathematics in Problems[M].PWN-Polish Scientific Publishers,1982.

[30]A Thayse.Boolean Calculus of Differences[M].Springer-Verlag,1981.

[31]J Fogarty.Invariant Theory[M].W.A.Benjamin,Inc.,1969.

[32]Paul Benacerraf and Hilary Putnam[M].Philosophy of Mathematics Prentice-Hall Inc.,1964.

[33]互子.易道中互-易經(jīng)體系[M].廣州：花城出版社,2009.

[34]徐芹庭.易圖源流[M].廣州：中國(guó)書(shū)店,2008.

[35]黃宗羲.易學(xué)象數(shù)論[M].北京：九州出版社,2007.

[36]張一方.中華歷代易學(xué)家傳[M].北京：北京藝術(shù)與科學(xué)電子出版社,2007.

[37]施維.周易八卦圖解[M].成都：巴蜀書(shū)店,2005.

[38]Zheng Jeffrey,Zheng Chris,Kunii T L.A Framework of Variant-Logic Construction for Cellular Automata,Cellular Automata-Innovative Modelling for Science and Engineering[M].InTech Press,2011：325-352.

[39]Zheng Jeffrey,Zheng Chris.A framework to express variant and invariant functional spaces for binary logic[J].Frontiers of Electrical and Electronic Engineering in China,2010,5(2)：163-172.

[40]Z J Zheng.Conjugate Visualisation of Global Complex Behaviour[J].Complexity International,1996,(3).

[41]Z J Zheng,C H C Leung.Visualising Global Behaviour of 1D Cellular Automata Image Sequences in 2D Maps[J].Physica A,1996,233：785-800.

[42]Z J Zheng.Conjugate Transformation of Regular Plan Lattices for Binary Images[D].PhD Thesis,Monash University,1994.

[43]Z J Zheng,A J Maeder.The Elementary Equation of the Conjugate Transformation for Hexagonal Grid[J].Modeling in Computer Graphics,1993：21-42.

[44]Z J Zheng,A J Maeder.The Conjugate Classification of the Kernel Form of the Hexagonal Grid[J].Modern Geometric Computing for Visualization,1992：73-89.