直驅式永磁同步風力發電機的H∞控制

蔡超豪

(沈陽工程學院 電氣工程系，遼寧 沈陽 110136)

0 引言

風力發電是開發和利用可再生能源的最好工具之一，具有廣闊的市場前景。省去齒輪箱的直驅式永磁同步風力發電機，因為具有機組壽命長、維護方便、效率高等優點，將成為未來風力發電發展的主要方向。因此，該機型的技術、運行特性、并網后功率的控制也相應地成為風電領域的重要研究課題。

近幾十年發展起來的H∞魯棒控制理論是一種比較成功且完善的理論體系，可以解決干擾抑制、魯棒穩定、信號跟蹤等問題。本文研究直驅式永磁風力發電機的H∞控制，應用Mat lab工具箱進行求解。

1 直驅式永磁同步風力發電系統的組成及其使用

直驅式永磁同步風力發電系統由風輪機、多極永磁同步發電機(PMSG)、PWM整流器、直流環節、PWM逆變器和電網組成(如圖1所示)，為了增加系統的可靠性和降低維修費用，取消了增速齒輪箱。由于永磁材料磁性能的改善和價格的降低，可用永磁體代替同步電機的勵磁繞組，省去了滑環，簡化了電機結構，并且永磁發電機與傳統發電機相比可以使極距減小，所以電機的轉速可以設計得較低，可以在20～200r/min之間，因而永磁發電機可以直接與風輪機相連，由變漿距風輪機直接驅動，構成直驅式永磁同步風力發電系統。

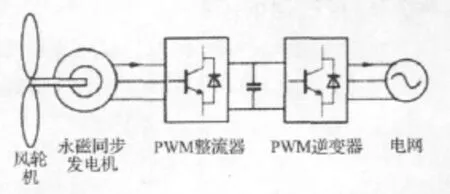
圖1 直驅式永磁同步風力發電系統的組成

PWM整流器將發電機發出的交流電整流成恒定直流，并提供一個可供最大功率點追蹤控制算法使用的直流信號和功率信號，實現最大功率控制;對整流器進行矢量控制，可以實現有功功率和無功功率的解耦控制。直流環節為PWM逆變器提供一個合適的直流電壓，使得逆變器向電網輸出一個期望的電流，以傳輸有功功率和無功功率。

發電機的單機容量為3～5 MW，也可以在每一臺發電機機端配置整流器，通過直流母線實現與風電場其他機組(群)的并聯運行，既提高了可靠性，又改進了效率。風電場由一臺大容量公用逆變器把直流母線的直流電轉換成50Hz的交流電，電壓可以達12kV，以直接并入當地電網使用，還可以經變壓器升壓至更高電壓后并入更高壓電網傳輸到遠處。

由于風能本身的波動性、隨機性，使得并網運行的風電機群輸出的有功功率也具有波動性、隨機性，因此機群輸出有功功率的控制目標是:在保證單臺風電機組安全穩定運行的基礎上，最大效率地利用風能，輸出恒頻恒壓的電量。

由于風電機群具有一定的無功功率調節能力，所以無功優化的控制目標為:提高風電機群與接入系統的電壓穩定，依據風速預測和地區系統無功優化方案，確定機群的無功輸出及電壓水平，以保證風電機群并網母線節點及系統關鍵節點的電壓穩定。

本文著力研究利用H∞控制方法對有功、無功功率控制參考值的跟蹤及內外部干擾的抑制，保持系統的安全運行。

2 直驅式永磁同步風力發電系統矢量控制時的數學模型

在兩相同步速旋轉d，q坐標系下，當采用定子磁場定向矢量控制，并將定子磁鏈矢量定向在d軸上，直驅式永磁同步風力發電系統矢量控制時的數學模型為［1］

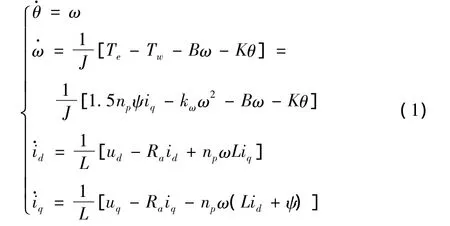
式(1)中第1、2式為風力發電機系統的轉子運動方程，式中θ，ω為轉軸角位移和機械角速度，TW為風能轉換到輪轂上的機械轉矩

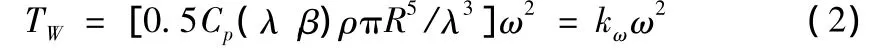
式中:kω=0.5Cp(λ，β)ρπR5/λ3，ρ為空氣密度，R 為風力機槳葉半徑，Cp(λ，β)為風力機的風能利用系數，β為槳距角，λ=ωR/υ為葉尖速比，υ為風速。

Te是發電機的電磁轉矩J，B，K分別為風力發電系統的機械轉動慣量、轉動粘滯系數和扭矩系數。

式(1)的第3、4式為基于d-q同步旋轉坐標系的發電機電壓方程，式中u，i分別表示電壓和電流，下標代表d，q軸分量，設d軸和q軸電感相等，即Ld=Lq=L，Ra為定子電阻，np為發電機磁極對數，ψ為每對磁極產生的磁鏈。

3 直接反饋線性化

直接反饋線性化(DFL)是我國學者提出并發展起來的基于系統輸入-輸出描述的一種反饋線性化方法［2］，可以將非線性系統在全局范圍內進行線性化處理［3、4］。與基于微分幾何理論的線性化方法對比，它們采用了不同的描述方式和處理方法，得到相同的線性化效果。DFL的優點是所用的數學工具簡單，物理概念清晰，適合于工程應用。

對式(3)、(2)進行坐標變換:采用狀態變量的偏差量為輸出變量，得輸出方程

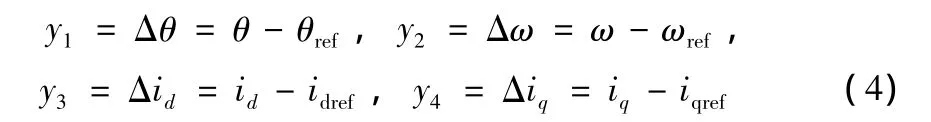
式中 θref，ωref，idref，iqref為選定的參考值。將式(4)對 t求導得

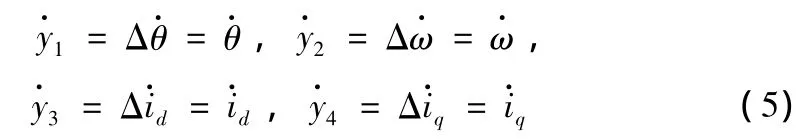
將不確定參數Ra，B，K用標稱值和偏差值之和表示(溫度變化引起Ra的偏差，轉速變化和轉軸的柔性變化引起B，K的偏差)

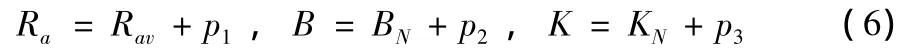
將式(4)～(6)代入式(1)，得出具有參數攝動陣ΔA(t)和有界擾動的不確定系統

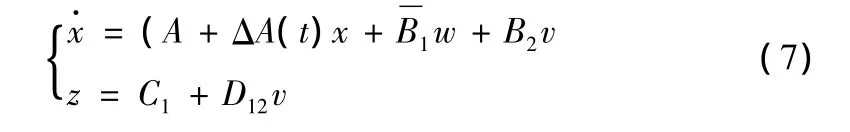
式中 x=［Δθ Δω ΔipΔiq］T

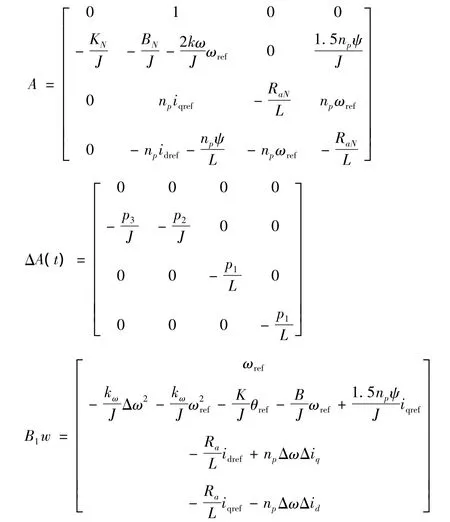
B1w包含非線性內容或不確定值，代入參數的數值后，可估計出其上界

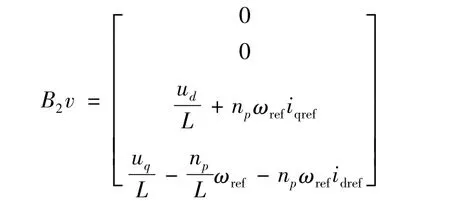
設B2v第3、4行分別等于v1，v2，它們被稱為虛擬控制變量，即

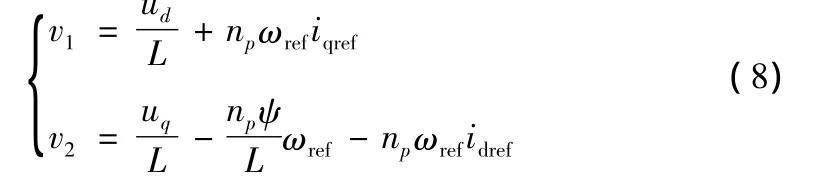
于是，B2v可寫成

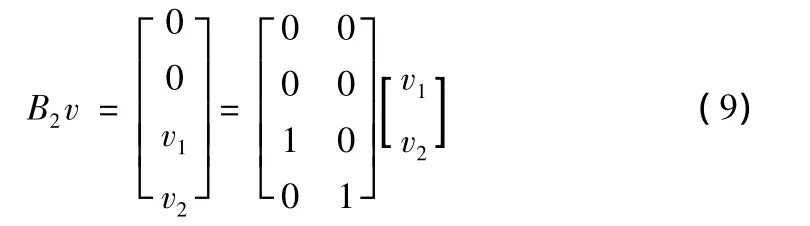
4 H∞控制器的求解

式(7)符合參數不確定系統的H∞控制標準形式［6］，第1式為被控對象，其中ΔA(t)為參數攝動陣，可描述為

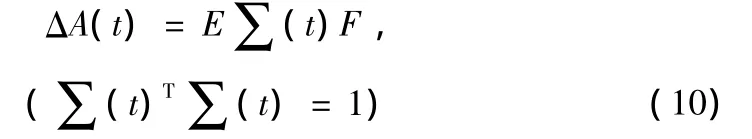
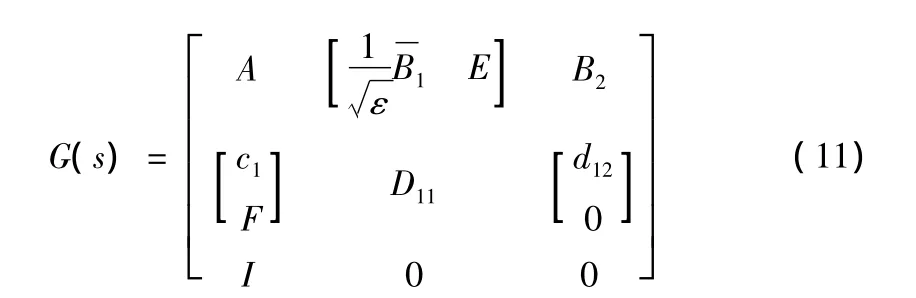
可用以求解具有魯棒穩定、干擾抑制性能的狀態反饋控制器。式(11)中ε＞0，ε越小，意味著系統對干擾抑制性能越好，但過小的ε將會削弱系統的魯棒穩定性。式中為零矩陣。

式(7)的狀態反饋控制器為

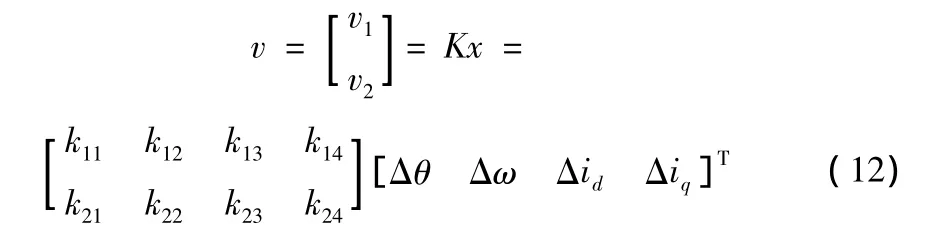
式中K為反饋系數，可以用求解Riccati不等式的方法或利用MATLAB軟件中μ-分析與綜合工具箱的hinffi.m函數求取［7］，命令如下 P= ［A，B1，B2;C1，D11，D12］

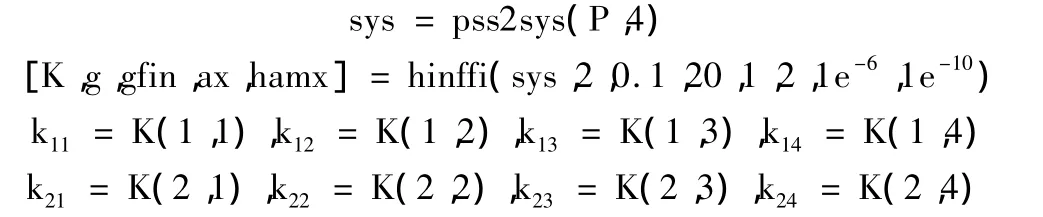
由式(8)、(12)便可得出直驅式永磁同步風力發電系統的非線性H∞控制律:

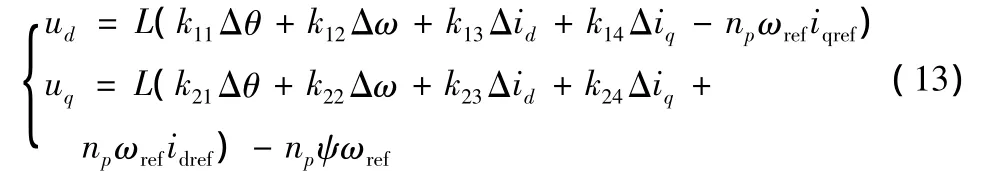
5 算例及計算機仿真

直驅式永磁同步風力發電系統的參數如下:額定功率PN=2 MW，額定電壓 UN=4 kV，風機額定轉數 ωg=23.87 r/min=2.5 rad/s，發電機極對數np=40，永磁體磁鏈 ψ=0.5634 Wb，定子電阻 RaN=0.01 Ω，定子電感 L=0.003 H。額定風速 υr=13 m/s，空氣密度ρ=1.225 kg/m3，葉片半徑r=42 m，等效轉動慣量J=8000 kgm2，轉動粘滯系數BN=3，扭矩系數KN=2。在運行過程中，不確定參數RaN，BN，KN變化可達其標稱值±50℅。試設計H∞控制器并進行計算機數字仿真。

取 θref=0，ωref=2.5 rad/s，idref=0 A，iqdref=260 A。取可能發生的最大偏差值:p1=0.005 Ω，p2=1.5，p3=1，計算式(7)的各項系數，按式(11)指定E，F，取式(12)中ε=100。得

選定加權函數c1和d12，(由式(1)、(13)構成仿真模型來進行加權函數的優化)。

求得狀態反饋控制器的反饋系數K

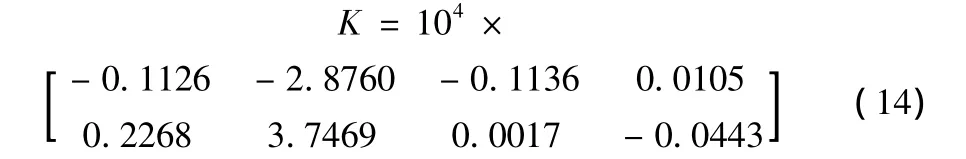
得上述直驅式永磁同步風力發電系統的H∞反饋控制律為

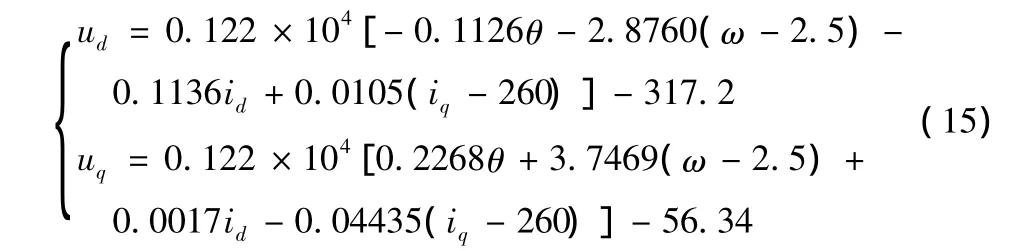
為了節省篇幅，給出下列一種運行情況作為例子進行仿真:設不確定參數Rc=0.01+0.005sintΩ，B=3+1.5sin2t，K=2+sin3t;隨著風速變化風力機的轉速曲線如圖2所示。發電機所希望的輸出有功功率(期望值)為 1.8 MW，試作仿真曲線。

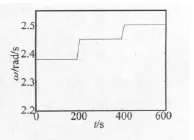
圖2 無刷雙饋型風力發電機的轉速ω

圖3給出了當系統具有如上參數攝動和擾動時的仿真曲線，(a)、(b)分別為風力發電機輸出有功功率、無功功率，實線為響應值，虛線為期望值(如將視圖放大，虛線可以看得更為清楚)。圖4(a)、(b)分別為發電機定子d、q軸電流響應值及期望值曲線，圖5(a)、(b)分別為H控制器的輸出電壓 ud、uq。

從仿真結果可以看出系統具有很好的跟蹤性能，實際響應值跟蹤期望值，不受不確定參數和風速變化的影響。

6 結束語

本文對直驅式永磁同步風力發電機的H∞控制進行了研究，建立了直驅式永磁同步風力發電機的魯棒控制模型，根據H∞控制理論，利用MATLAB工具箱設計了H∞控制器。仿真結果表明，在該控制器作用下，直驅式永磁同步風力發電機具備參數攝動鎮定性能和干擾抑制性能，風速變化雖然使風力發電機的轉速隨之變化，但輸出的有功功率、無功功率的實際響應值仍能很好地跟蹤期望值曲線，發電機轉子d、q軸電流響應值跟蹤期望值曲線，安全可靠地獲取最大風能，向電網輸送恒頻恒壓的電能。

［1］尹明，李庚銀，張建成，等.直驅式永磁同步風力發電機組建模及其控制策略［J］.電網技術，2007，31(15):61-65.

［2］高龍，等.非線性系統的 DFL及隱動態［J］.清華大學學報，1996，36(9):1-9.

［3］張春朋，林飛，宋文超，等.基于直接反饋線性化的異步電動機非線性控制［J］.中國電機工程學報，2003，23(2):99-102，107.

［4］蔡超豪.矢量控制異步電動機的非線性H∞控制［J］.中小型電機，2004，31(1):49-52.

［5］丁剛，王勛先，韓曾晉.感應電機的H∞抗干擾控制［J］.控制理論與應用，1999，16(4):483-486.

［6］申鐵龍.H∞控制理論及應用［M］.北京，清華大學出版社，1996:136-151.

［7］Doyel J，Glover K.The mu-analysis and synthesis toolbox of Malab［D］.MathWorks Inc，1998.