用龍格-庫塔法優化一種模糊控制器

王江榮

(蘭州石化職業技術學院 信控系，甘肅 蘭州 730060)

0 引言

帶有可自調整因子的模糊控制器輸出的一般形式為U=-{α(t)E(t)+(1-α(t))EC(t)}(0＜α＜1)，其中 E(t)和 EC(t)是模糊論域上量化后t時刻的誤差和誤差變化。α(t)是時刻t的可調整因子(可在線實時調整)。U=U(t)是模糊論域上的輸出，其值取決于對誤差和誤差變化的加權。對可調整因子α(t+1)=α(t)+Δα的在線修改往往根據人們的經驗或實驗調試確定，這樣的修改會有一定的主觀性和盲目性。本文利用四階龍格一庫塔公式逼近被控對象，再結合梯度下降法實現了可調整因子中的Δα(t)中的在線修改和在線優化，仿真曲線表明，在響應時間相同的情況下，具有優化后的調整因子的模糊控制器在穩定時間、超調及魯棒性等幾方面的性能均優于未優化的模糊控制器，顯著地改善模糊控制系統的控制精度和穩態性能。

1 龍格-庫塔

龍格-庫塔法是求解常微分方程初值問題的有效數值方法。這種方法的特點是區間［xk，xk+1］上取N個點，以這N個點的斜率值f(xk，yk)的線性組合為加權平均斜率，構造近似公式

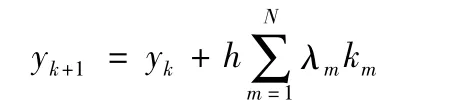
其中 k1=f(xk，yk)

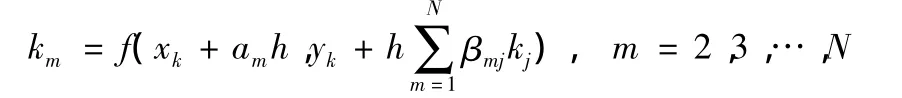
確定這些常數的原則和方法是:將精確解y(xk+1)在xk作Taylor展開，ki在(xk，y(xk))點作二元Taylor展開，將展開式按h的冪次整理后，令h0，h1，h2，…等項的系數為零，使Tk+1首項中 h的冪次盡量高。

在近似公式中取N=4，可得到四階龍格-庫塔法公式yk+1其中 k1=f(xk，yk)

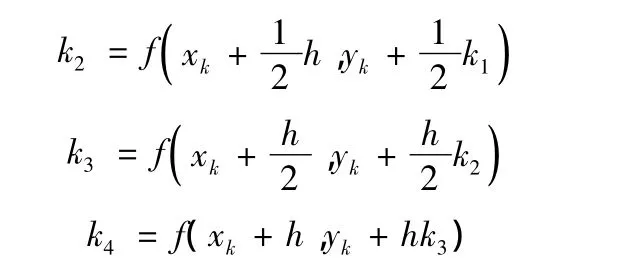
四階龍格-庫塔法的優點是它的精確度高且是一步法，即已知yk就可以算出yk+1，另外容易用程序實現。

2 可調整因子α(t)的自動優化過程

設t時刻的可調因子值為α(t)，t時刻算出的α(t)的增量為Δα(t)，t時刻后算出的修改因子為 α(t+1)=α(t)+Δα，Δα 可由t時刻采樣所得的誤差e(t)求得。對α(t)的實時修改和優化具體推理過程如下:

設t時刻的誤差e(t)和誤差變化ec(t)量化后得到模糊論域上的誤差為E(t)和誤差變化EC(t)，則t時刻模糊控制器在模糊論域上的輸出為

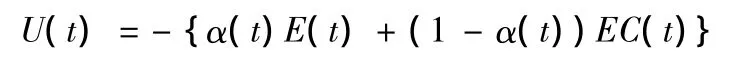
該輸出乘以輸出比例因子Ku就得到t時刻的控制器的實際輸出 u(t)，即

設被控對象的狀態方程(可用MATLAB軟件將被控對象的傳遞函數H(s)轉化為狀態方程)

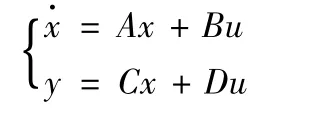
其中，A，B，C，D 是系數矩陣。u為式(1)。

用龍格-庫塔法逼近被控對象如下

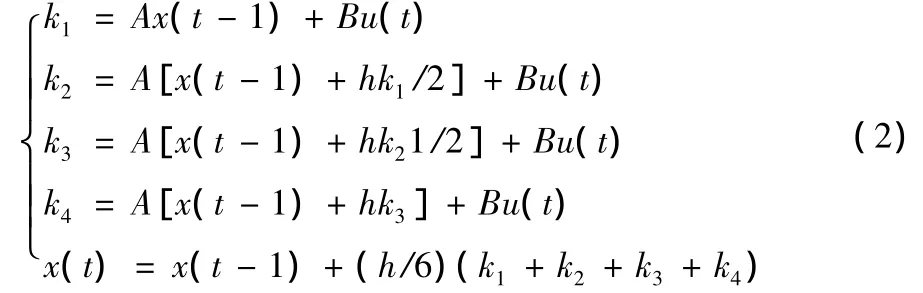
則t+1時刻系統的輸出為

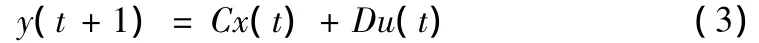
t+1時刻的誤差

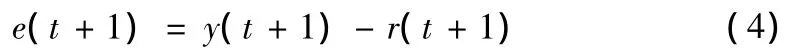
這里的r(t+1)是系統輸入。

Δα(t)的計算

這里的λ和μ是比例系數。

按負梯度方向求t時刻可調整因子α(t)的增量Δα(t)，即

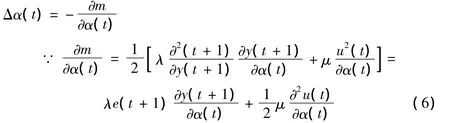
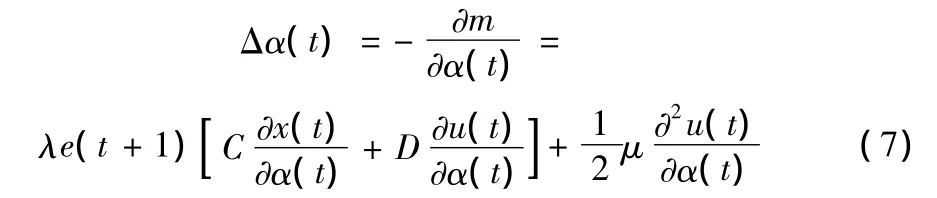
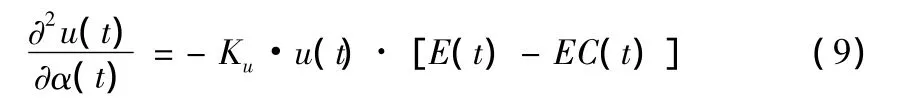
由(2)可得

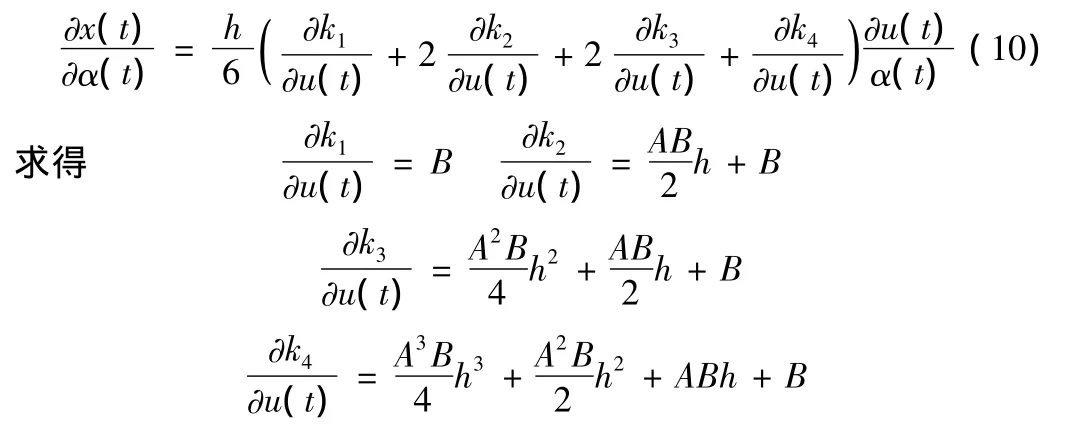
將上四式代入(9)得

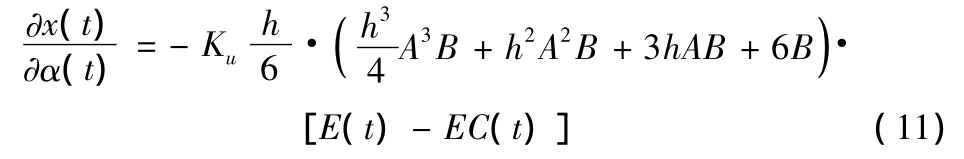
將(8)、(9)及(11)代入(7)得

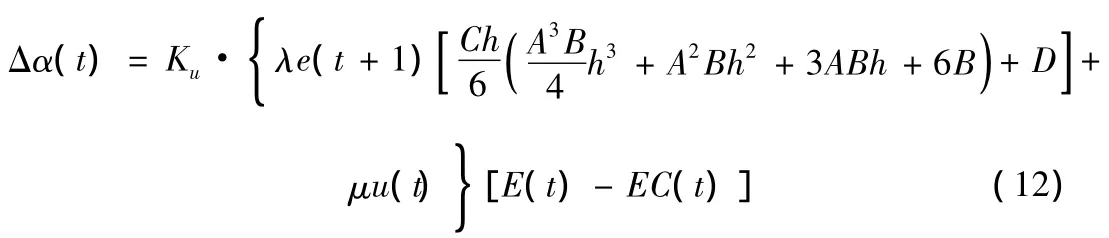
當系統確定時，即A，B，C，D及h確定時

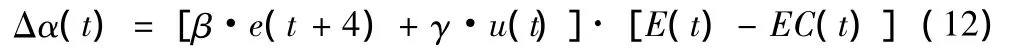
由(12)知只需調整參數β和γ就能計算出Δα(t)(并不依賴狀態方程中的系數矩陣)，進而實現對模糊控制器的優化。

3 仿真結果

利用MATLAB進行仿真實驗

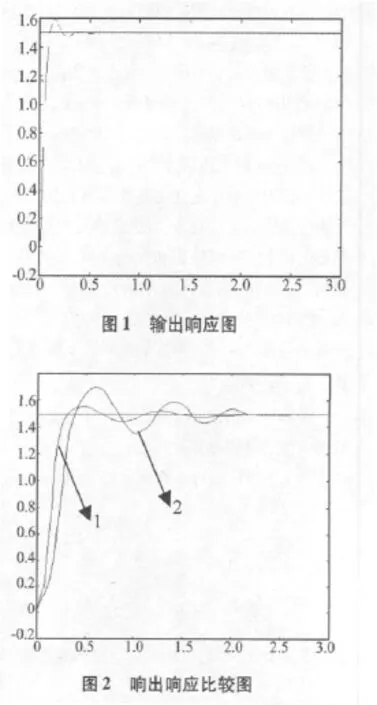
(2)假設系統的模型可以用二階加純滯后表示，即傳遞函數為采樣時間間隔為 ΔT=0.01 s，輸入為階躍函數r(t+1)=1.5，α 的初始值取 0.5，β=0.065，γ =0.015時，系統的輸出響應為如圖2中的曲線1.圖2中的曲線2是沒有加修改的 Δα(t)的情形。可以看到用龍格-庫塔法進行修改 Δα(t)，模糊控制器的輸出曲線上升時間短(到達穩態)，且具有很好的穩態性能(振蕩幅度小)，說明本文方法起到了優化效果。

4 結束語

本文利用龍格-庫塔法改進了自尋優模糊控制器的可調因子α(t)，實現了對α(t)的在線實時優化。從仿真曲線表明，在響應時間相同的情況下，具有優化后的調整因子的模糊控制器在穩定時間、超調及魯棒性等幾方面的性能均優于未優化的模糊控制器。它最大限度地識別和利用控制系統所提供的信息，不斷的修正控制規則，使控制器本身的控制規律適應系統的需要，從而顯著地改善模糊控制系統的控制精度和穩態性能。

［1］李國勇.模糊控制神經控制和智能控制論及應用［M］.北京:電子工業出版社，2010(1):164-224.

［2］雷德明.一種新型自學習模糊控制器［J］.信息與控制，2000，29(6):559-562.

［3］李榮華，等.微分方程數值解法［M］.北京:高等教育出版社，2002(8):59-60.

［4］侯忠生.非參數模型及其自適應控制理論［M］.北京:科學出版社，1999:30-80.

［5］劉航，徐社.MATLAB在模糊控制系統設計與仿真中的應用［J］.計算機應用研究，2001(1):27-28.