關于超網絡的一點思考

王眾托

(大連理工大學系統工程研究所,大連 116085)

關于超網絡的一點思考

王眾托

(大連理工大學系統工程研究所,大連 116085)

在探討超網絡的內涵時提到,除了Nagurney所著重研究的多層超網絡之外,還有一類基于超圖(hypergragh)的超網絡(hypernetwork)值得關注.超圖的特點是圖中的邊可以連接兩個以上的節點,這對研究信息與知識網絡的研究與應用會有獨特的用途.以知識的超網絡表述為例,介紹了基于超圖的超網絡的簡單應用.

復雜網絡;超網絡;超圖

現在可以說我們是生活在一個網絡世界里,各種設施和事務都是通過網絡聯系起來的.例如交通運輸網絡是由道路把站點連接形成的網絡.電力網絡是由發電廠、變電所和用戶通過輸電和配電線路連成的網絡.計算機網絡可以看作是自主工作的計算機通過通信介質如光纜、雙絞線、同軸電纜或者無線電波等相互連接形成的網絡.神經系統可以看作是大量神經細胞通過神經纖維相互連接形成的網絡.上面提到的是有形的網絡,還有許多由于社會關系(業務活動、血緣與人際交往等等)而形成的無形網絡.人類社會中的網絡的產生和發展推動了社會的進步,例如交通運輸系統給人員與貨物的流動帶來方便,促進了商貿和工農業的發展;信息系統給資金的流轉、商務的流通帶來很多的方便,提高了生產效率和生活質量.但是另一方面像傳染病的流行和網絡病毒的傳播,電力網的局部故障引起大面積的停電,核輻射的傳播給人們的健康帶來了威脅,這又是由于網絡的存在而帶來的危害.因此對自然網絡和人工網絡的認識和干預(構建、運行和防護)就成為科學技術所要解決的問題之一.

典型的網絡是由許多“節點”與連接兩個節點之間的一些“邊”組成的,其中節點用來表示實際系統中不同的個體,連接的邊則用來表示兩個節點之間具有某種特定的關系.用圖形表示就是常見的網絡圖.在節點之間通過邊有網絡流(物流、能流、信息流、資金流)在流動.隨著網絡規模的日益擴大和連接的日益復雜,人們對網絡除了從各自專業的角度加以研究外,還關注各類網絡在結構和運行上的共性,希望能夠用抽象的數學工具來加以描述和分析.從18世紀數學家歐拉對所謂“Konigsberg七橋問題”的建模和分析,從而開創了數學中圖論這一分支以來,在運籌學中的網絡系統分析中對最短路徑、最大流以及最小費用流等方面,還有對時間流進行分析與設計的網絡計劃技術等,有了一些解決實際問題的研究.隨著交通事業的發展,出現了鐵路網、公路網、航空網,信息化的發展產生了各類信息網.網絡化的發展,出現了許多復雜的網絡,這些網絡節點和邊的數量眾多,結構復雜,例如互聯網(Internet)的用戶已經是數以億計,由于缺少統一的管理,時至今日沒有任何一個人或組織能夠知道互聯網上所有的路由器到底是怎么聯結在一起的.再就是連接的多樣性,有的松散有的緊密,屬性也有差異.網絡節點和邊又都可能有復雜的動態行為.人們在運用網絡滿足自己的要求,常常是多目標或多準則的,而網絡的存在又提供了更多的選擇性,因而使得決策和優化問題更加復雜.生活實踐和理論研究都需要對這樣的復雜網絡(complex network)進行深人的認識與分析.

到目前為止,科學家們還沒有給出復雜網絡精確嚴格的定義,但我們已經可以從上面列舉的復雜網絡的特征來理解它的含義.

一個網絡的功能與它的結構密切相關,因此要從研究網絡的結構人手.最初對復雜網絡的拓樸結構是用具有一定規則的結構表示的,形成所謂規則網絡,但其適用范圍過窄.20世紀60年代出現的隨機圖理論,適應了網絡的不確定性特點,開創了復雜網絡的系統性研究.在這種方法中,兩個節點之間是否有邊相連不再是確定的事情,而是根據一個概率決定.但大多數實際的復雜網絡結構并不是完全規則或完全隨機這兩個極端,而是要比規則網絡和隨機網絡更為復雜.因此需要探索和發現網絡中的一些特殊的性質.當時有兩項研究成果使得研究工作得到了很大的推進,即發現某些網絡中的小世界效應(small-world effect)和無標度特性(scale-free property)[1-2].科學家在研究節點的度(與該節點連接的邊的數目)的分布時,發現大量真實網絡的節點度服從冪率分布(連接邊多的節點少而連接邊少的節點卻非常多),而不是像隨機網絡那樣服從鐘型分布.我們把節點度服從冪律分布的網絡叫做無標度網絡(scale-free networks),Barabási和Albert把真實系統通過自組織生成無標度的網絡歸功于兩個主要因素：生長和優先連接,而他們的網絡模型(BA網絡)正是模擬這兩個關鍵機制設計的[2-3].

這些成果使得人們對于實際存在的網絡的生成機制、傳播機制、茁壯性和脆弱性等有了新的認識.隨后有關復雜網絡的研究有了長足的進展.

1 超網絡

但是在有些情況下,用一般的網絡圖并不能完全刻劃真實世界網絡的特征.在研究超大規模的網絡系統時,會出現網絡中的網絡的問題.如果用原來簡單或有向圖的方法來處理這類問題,就很難理清各個網絡之間的關系.因此就出現了超越一般網絡的網絡系統問題.人們常常把規模巨大、連接復雜、節點具有異質性的網絡稱為超網絡,例如認為互聯網是一種超網絡,但這只是從常識上的一種稱呼,沒有明確定義.另有一種對超網絡的理解,是認為超網絡是網絡組成的網絡.最早明確提出“超網絡”概念的是美國科學家Nagurney等[4-5],她在處理物流網絡與信息網絡、資金網絡相交織的問題時,把高于而又超于現存網絡(“above and beyond”existing networks)的網絡,稱為超網絡(supernetwork).

Nagurney所研究的超網絡具備一種或幾種特征：a.多層特征,例如交通運輸網就有物理層、業務層和管理層;信息網絡協議也是多層的.層內和層間都有連接.b.多級特征,例如企業的信息網絡有部門、公司、總部等級別.同級和級間都有連接.c.它的流量可以是多維的,例如鐵路、公路、水運和航空都是既有客運又有貨運.d.多屬性或多準則的,例如在城市中出行不僅有路徑選擇,而且有方式(駕車、公交、步行)的選擇,運輸網絡需要同時考慮時間、成本、安全舒適等.e.存在擁塞性,不僅交通運輸網絡,而且信息網絡也存在擁堵問題.f.全局優化和個體優化需要協調.

超網絡模型可用來描述和表示網絡之間的相互作用和影響.它可以將許多不同層次、不同標準的決策者之間的關系用關系函數來表示,在建立關系過程中,決策者必須付出一定的代價,如需付出物品、時間、金錢等.隨著關系層的增加,交易的成本和不確定性就會增加,因此必須給關系附加描述值.為了以較小的代價取得最大的利潤,決策者一定會考慮最大關系值,因此決策者既要找到與網絡中其它決策者交易的組合優化,又要找到關系層的組合優化.超網絡的構架為研究網絡之間的相互作用和影響提供了工具.它可以用一些數學工具對網絡上的流量、時間等變量進行定量的分析和計算,這些數學工具包含：優化理論、博弈論、變分不等式及可視化工具等.可以舉出下面一些超網絡的例子：

a.供應鏈與社會網絡結合的超網絡模型[5]這是由社會網絡和供應鏈網絡組成的超網絡.這兩個網絡都由三層決策者構成,社會網絡中的流是各層之間的關系,供應鏈網絡中的流是產品之間的交易.

b.電子商務中的供應鏈超網絡模型 這是一個包括m個商家和n個需求市場的供應鏈超網絡,其中.商家與需求市場的交易流程(訂貨、付款、傳遞)都在互聯網上進行,脫離了傳統的物流配送系統.

c.回收超網絡模型 一個由m+n+o個單位組成的回收超網絡,其中包括m個可造產品資源地,n個回收商和o個需求生產商,并任意取第i個資源地,第j個回收商和第k個需求生產商進行討論.有一些載能資源恢復理想中的使用價值會比由原材料生成所需要費用更高,不值得回收,因此對它們的處理就是使之銷毀并掩埋.

d.閉環供應鏈超網絡模型 由原材料供應商、生產商、零售商、需求市場和回收商組成的I+J+K+M+N個閉環供應鏈超網絡.其中,包括I個生產商總數,J個零售商總數,K個需求市場總數,M個回收商總數,N個原材料供應商總數,并任意取第i個生產商,j個零售商,k個需求市場,m個回收商,n個原材料供應商.

前面的一些超網絡是從網絡結構來考慮的,而現實生活中還有另外一些超網絡是從聯系方式來考慮的.例如：

a.社會網絡[6]在社會網絡中,點表示一個人或一群人,通常稱為行動者,他們之間如果交往或接觸就用一條邊將其連結.這樣的連結方式可以是友誼、合作、貿易關系等.例如貿易交往中,必須考慮多于3者之間的關系,如賣者、買者、經紀人.其它的例子中,不僅僅要考慮行動者參加行動的重要性,還要考慮其它的一些因素,如參加行動的時間、地點等.

b.蛋白質網絡[6]在一個有機體蛋白質水解過程中,對多蛋白質復合物的系統描述需要蛋白質成員之間有組織的數據.這個組織最普通的形式是蛋白質之間的相互反應網絡和復合物交叉圖.在前一種表示中,網絡的點代表蛋白質而邊連著相互反應的蛋白質.然而,這個表示并沒有考慮到多蛋白質復合物.在復合物交叉圖中,點表示復合物,而如果兩個復合物之間有一個或多個共同的蛋白質的話,就用一條鏈將它們連結.很明顯,這后一個表示并不能提供關于蛋白質的信息,因此需要使用超網絡來提供蛋白質和多個共同的蛋白質成員之間的信息[7].

c.食物網[6]在生態學中,營養關系通常用表示為有向圖(子圖)的食物網來表示,其中,點表示物種而鏈表示物種之間的營養關系[8].表示食物網的另一種方法是用競爭圖C(G)來表示,其中點集與食物網相同,當且僅當聯系的物種在食物網中有共同的獵物時兩點之間是連通的[9].在競爭圖中,僅僅知道兩個聯系的物種之間有共同的獵物,但并不知道為共同獵物競爭的整個物種群的構成情況.為了解決這個問題,需要建立競爭超網絡[10].

d.計算機網絡[6]在計算機領域中,若把多機系統中的處理機看作節點,處理機的集合作為超網絡節點集;把總線集作為超網絡的邊集,于是一個多機系統就抽象為一個超網絡.

e.知識網絡[11]現在已經存在的互聯網和各組織內部的內聯網也都可以看作是知識網絡,因為以信息為知識載體,在網上儲存了與流通著大量的知識.這類知識網絡由三層組成：技術層、知識內容層和人員層(社會網絡層).

2 基于超圖的超網絡

目前還有用超圖(Hypergraph)來定義的另一類超網絡.這類超網絡的英文名字叫Hypernetwork,有別于Supernetwork.超圖的概念是Berge[12]于1970年提出的,文獻[12-13]第一次系統地建立了無向超圖理論.超圖不同于一般圖論中的無向或有向圖的地方在于：后者的每一個邊只連接兩個節點,而超圖中的邊可以連接兩個以上的節點,所以稱之為超邊.

數學上超圖的嚴格定義為：

設V={v1,v2,…,vn}是一個有限集.若

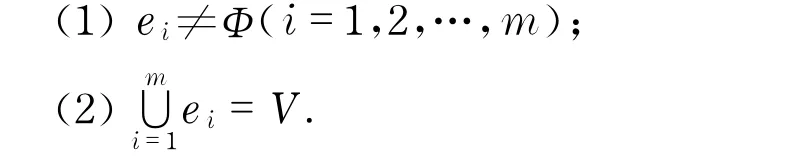
則稱二元關系H=(E,V)為一個超圖.V的元素v1,v2,…vn稱為超圖的頂點,E={e1,e2,…,em}是超圖的邊集合,集合ei={vi1,vi2,…,vij} (i=1,2,…,m)稱為超圖的邊.

超圖H的對偶H*稱為對偶超圖.如果對所有的那么,超圖H*=(E;V1,V2,…Vn)稱為H的對偶超圖.顯然,(H*)*=H.例如,研究圖1中的4個拱門

a1、a2、a3、a4.它們是由總共8類構件b1、b2、b3、b4、b5、b6、b7、b8組成的,每個拱門所用的構件不同.

圖1 4個拱門的圖形Fig.1 Diagram of 4 arches

如果用二分圖來表示構建和拱門的關系,可以畫出圖2來(見圖2).這里有兩類性質不同的節點,一類表示拱門,一類表示構件,這時節點的同質性失去了,在處理上就會帶來許多不方便.

圖2 用二分圖來表示4個拱門Fig.2 Representation of 4 arches by Bi-partition graph

如果用超圖表示其中的關系,以各構件b為節點,以a1(b1,b2,b3)、a2(b2,b3,b4)、a3(b4,b5,b6)、a4(b6,b7,b8)為超邊,就得到了如圖3所示的超圖.這些超邊表示出各拱門都是用哪些構件購成

的.假如以各拱門a為節點,以b1(a1)、b2(a1,a2)、b3(a1,a2,a3)、b4(a2,a3)、b5(a3)、b6(a3,a4)、b7(a4)、b8(a4)為超邊,就得到如圖4所示的超圖.其中的超邊表示各構件都用在哪些拱門上.

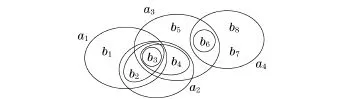
圖3 超圖表示的4個拱門Fig.3 Representation of 4 arches by hypergraph

圖3、圖4兩個超圖是互為對偶的.超圖在描述多個節點有連接的網絡時,有它的方便之處.例如在電話的通話業務中,每一個用戶可以用一個節點來表示.如果兩個人通話,可以用一般圖論中的邊來描述.如果是3個人召開電話會議,用一般圖論中的邊來描述,就得像圖5(a)中那樣,需要3個邊.如果用超圖來描述,則如圖5(b)那樣,使用一個超邊就行了.

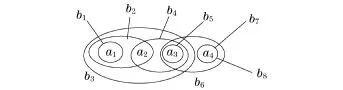
圖4 超圖3的對偶超圖Fig.4 Duality of Fig.3

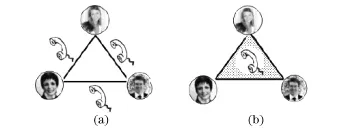
圖5 電話通話的圖形表示Fig.5 Representation of phone communication

從現有研究成果來看,關于超圖理論及其應用的研究是另外一條主線.這里可以提到的主要有以下幾個方面：

關于超圖理論本身的研究開始較早,文獻[14-17]分別研究了超圖理論的基本概念及基本性質.文獻[18]引人了超通路、超回路、超邊分解、分解超圖、k-超樹、單向超通路和單向超樹等概念,建立了有向超圖理論.文獻[19]研究了超圖的Helly性質、Ramsey數、橫貫與匹配、分數橫貫、著色等.文獻[20]研究了超圖的t-設計.

基于超圖的超網絡的應用方面,文獻[21]將超圖應用在大規模集成電路布圖設計中.文獻[22]提出一種“基于超圖的容錯VLSI處理陣列”,基于文獻[23]的成果,文獻[24-25]應用具有最佳連通性超圖的一些性質解決了多總線系統的分析和綜合問題.文獻[26]提出了一種基于優先記發式的超圖二劃分算法.文獻[27]給出了函數依賴集的超圖表示,提出了一種基于有向超圖的求最小覆蓋集的新算法.文獻[28]基于超圖模型生成了緊的無冗余XML文件.文獻[29]將超圖劃分方法應用在VLSI領域.文獻[30-32]將超圖與圖象處理相結合,建立了圖象鄰域超圖模型.文獻[33]對細胞動態交流系統建立了超圖模型.文獻[34-35]對數據挖掘中的聚類提出了新的算法且建立了超圖模型.文獻[36]將超圖應用在化學上,利用超圖的拓撲指數來識別化學中的化合物分子結構.文獻[37]用超網絡來辯別DNA切塊,文獻[38]用DNA超網絡對信息進行存貯和獲取.文獻[39]用進化超網絡對模式進行了分類,建立了進化變階的超網絡模型.超圖作為一類特殊的圖,不像一般圖論那樣和易于運用.它的應用也還沒有像一般圖論那樣成熟,但是在運用于復雜的網絡系統的描述和分析上,具有很大的潛力.

筆者認為,基于超圖的超網絡可以認為是廣義的超網絡中的一個子類,就像以Nagurney為代表所研究具有前面所述的6種特性的網絡,也是超網絡的一個子類.因為兩者像Nagurney所說的,都是高于而又超于現存網絡(“above and beyond”existing networks)的網絡.

3 基于超圖的超網絡在知識表述上的應用舉例

如何將網絡同知識的表示與組織結合起來,成為許多知識科學與知識管理研究者感興趣的話題之一.經過近年來的探索,知識網絡的概念逐步形成.知識網絡作為一個概念,早在1995年Beckmann[40]就提出過,他認為知識網絡指的是從事科學知識的生產和傳播的機構和活動.超網絡和超圖在知識的表述和處理(聚類、分類、集成等)中將會有很多的用途.可以用一個簡單的例子來加以說明[11].主題的辨識與提取是知識建模中的重要環節.長期以來認為通過超鏈可以找到圍繞著主題的文檔類,但這還不足,應該進一步研究辨識主題或者說生成主題的方法.一類含有同樣主題的文檔是可以聚類的,但主題是隱含在其中的.有時候一個主題是可以用一個表述能力很強的詞語來描述的,也有時候需要一組相關的詞語來描述.有的詞語有利于檢索,但并不一定是好的描述符.這又和具體任務有關,有的是為了尋找一個很狹小的范圍內的具體內容,有的是要在一個很寬泛的范圍內收集涉及面很廣的知識.兩者對描述符的要求就不一樣.從直覺上來判斷,如果一個或幾個詞語能夠明確回答“這個主題是關于什么的”問題,就是好的主題描述符.如果一個或幾個詞語能夠回答“什么是能夠得到類似的信息的好的詢問詞語”,就是好的鑒別符.

為了確定主題的描述符和鑒別符,需要分析詞語、文檔和主體之間的關系.文獻[41]建議使用超圖來表示這樣的關系.我們可以把一組文檔看做一個超圖H=(T,D),其中每一個節點t∈T對應于一個詞語,每一個超邊d∈D對應于一個文檔.一個超邊d是一個T中元素的多元集,把一個文檔抽象地表示為像一個裝了詞語的口袋.可以把這種超圖稱為以文檔為中心的超圖.

對應于每一個以文檔為中心的超圖H=(T,D),有一個以詞語為中心的超圖H*=(D,T),它的節點對應于文檔而超邊對應于詞語,超邊是文檔的多元集.超圖H*是超圖H的對偶超圖.圖6中的超圖,表示的是由3個文檔A、B、C和其中包含的詞語1,2,3,4之間的關系.

圖6 用超圖表示文檔(取自于文獻[41])Fig.6 Representation of documents(from[41])

圖6(a)是以文檔為中心的超圖

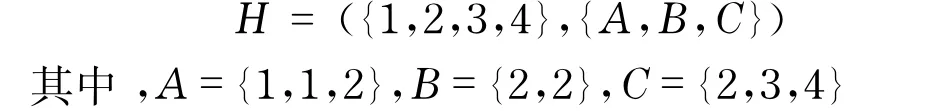
圖6(b)是它的對偶超圖

在圖6中,圓圈表示超邊而小三角表示節點.圖6(a)與圖6(b)中節點和超邊的連接上的數字表示的是該節點在超邊中出現的次數.例如節點1和超邊A的連接上標注的2,表示詞語1在文檔A中出現2次.

這里這樣定義關聯矩陣：對一個由m個文檔和n個詞語的以文檔為中心的超圖來說,其關聯矩陣的m行對應于文檔,n列對應于詞語.矩陣的元素

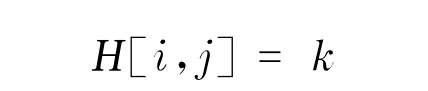
其中,k是第j列的詞語在第i行的文檔中出現的次數.我們還可以知道,對偶超圖的關聯矩陣是原超圖關聯矩陣的轉置.可以使用關聯矩陣的某些性質來反映詞語在文檔中的描述能力和鑒別能力.詞語j在文檔i中的描述能力可以用下列函數來衡量

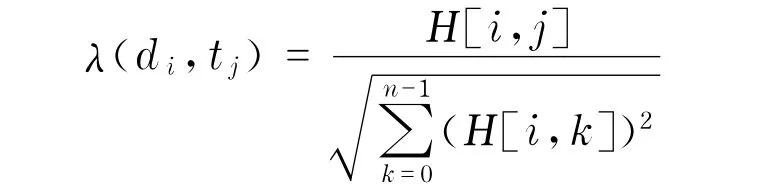
利用這一函數(它的數值在0與1之間)可以構成加權的以文檔為中心的超圖,如圖6(c)所示,它可以稱為d-超圖.從圖中可以看出,不同的詞語的描述能力是不同的,例如詞語2對文檔B的描述能力最強,詞語1對文檔A的描述能力比詞語2強.

為了度量詞語對文檔的鑒別能力,可以使用下列函數

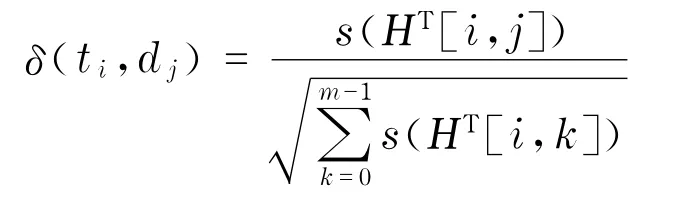
其中的s(k)是當k＞0時其值為1,當k=0時其值為0.這個函數的值也是在0與1之間.如果第i個詞語不出現在文檔j之中,則函數值為0;如果第i個詞語除了出現在文檔j之外不再出現在其它文檔之中,則該函數值為1,因而可以說這個詞語完全鑒別出該文檔.這個函數與詞語在文檔中出現的次數無關.利用這一函數可以構成加權的以詞語為中心的超圖,如圖6(d)所示,它可以稱為t-超圖.其中,詞語1完全鑒別出文檔A.

對d-超圖與t-超圖來說存在關系

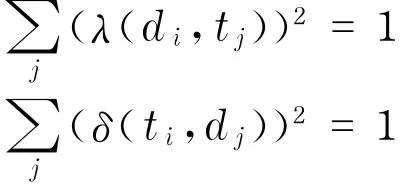
上面這種選擇最好的描述符合鑒別符的方法僅僅是對文檔而言的,還需要為主題選取好的描述符和鑒別符.主題總是要涉及多個類似的文檔或詞語,因此需要研究文檔的相似性和詞語的同時出現性.

兩個文檔di與dj的相似性可以按照眾所熟知的余弦測度來衡量

圖7(a)使用d-超圖來闡明文檔的相似性.從圖中可以看出,文檔D和E是相似的.圖7(b)使用t-超圖來闡明同時出現性.可以看出,詞語3和4是同時出現的.怎樣識別一個文檔的主題的最好的鑒別符呢?如果一個詞語他所鑒別出來的文檔是和某一已知文檔相似的,那么這個詞語就是這個文檔的好的鑒別符.如果用公式,則可用函數

表述.可以把詞語ti對文檔dj的鑒別能力,看作是文檔dj與由ti鑒別出來的其它文檔的相似性的平均值.

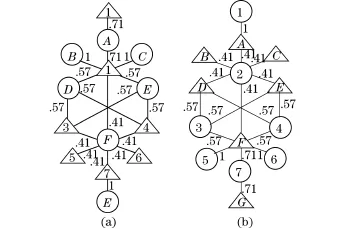
圖7 用超圖來說明文檔的性質圖(取自于文獻[41])Fig.7 Explanation of features of documents(from[41])

下面再來看主題的描述符.前面曾經非正式地說到過,主題的描述符就是在主題的環境中經常出現的詞語.一個詞語在主題中的描述能力可以用前面用到的對文檔相似性和文檔中詞語的描述能力來計算.這樣就能夠用函數來度量

一個詞語tj在文檔di的主題中的描述能力,是詞語tj作為與文檔di相似的所有文檔的描述符的質量指標.如果沒有其它文檔和di相似,或者tj沒有出現在與di相似的其它文檔之中,則tj在di的主題中的描述能力為0.在圖7中,詞語2,3,4在文檔D、E、F的主題中都是好的描述符.但是3,4是這一主題好的鑒別符,而2卻不是.因為2雖然在該主題中,但卻不僅在這一主題中.在這3個文檔中,只有D和E是聚焦在這一主題上的.文檔F包含了這一主題同時出現的詞語,但不是這一主題的獨有詞語.

以上僅僅是一個簡單的例子用來說明這類超網絡的應用,這方面還有很大的發展空間.

4 超網絡進一步發展的一點思考

超網絡的提出只是近幾年的事,目前它也只是一個概念,其邊界并不十分清晰.對于一些實際問題,僅僅在利用變分不等式和超圖的基礎上建立了一些模型,提出了一些解法.對超網絡本身還沒有眾所公認的定義.對于什么樣的網絡可以算作超網絡也還有一個逐步明確的過程.但是從上面已經列舉的一些事例來看,由于社會經濟和科學技術的網絡化的進一步發展,這類網絡問題逐漸呈現,像對有關復雜網絡的研究一樣,人們開始找到了它的一些特征,以及合適的描述方法.

對照復雜網絡的含義,可以說超網絡也是一類特殊的復雜網絡.上世紀末和本世紀初國內外都掀起了對復雜網絡研究的高潮.特別是人們擺脫了還原論的局限性,進而開始研究網絡各組成部分的相互影響,這正是超網絡的研究內容.在文獻[42]中一批權威作者經過討論提出了當前網絡研究的10個主要問題,其中談到了有關“網絡的網絡”問題,即研究不同性質網絡間的相互作用問題.可見超網絡問題將逐步進人網絡研究的主流.特別是在系統工程界近年來開始研究所謂“系統的系統,SoS”,如果系統可以用網絡來描述,那么“系統的系統”就可以用“網絡的網絡”也就是超網絡來描述.對超網絡的研究,和對一般的復雜網絡的研究一樣,將會有助于理解“復雜系統之所以復雜”這一極其重要的問題,這也就是說,超網絡問題的研究不僅有其實際意義,而且也對系統復雜性的探索開辟了一個新的途徑.超網絡概念的提出,使得人們對一些多層、多級、多維網絡流、多屬性和多準則的網絡問題有了新的認識和理解,但是我們還只是在復雜性的密林中剛剛找到一些小道,還需要開辟新的道路.盡管在文獻[6]中用到了復雜超網絡這一提法,但依我們的看法,除了一些極其簡單的超網絡問題可以憑經驗解決外,大多數超網絡都是復雜的超網絡,都可以看作是一類特殊的復雜網絡,這種復雜性主要表現在屬性上,而不是在規模上.所以不必另加復雜這一定語.正是由于其屬性的特點才使超網絡問題需要另辟蹊徑專門加以研究.

依筆者的淺見,對超網絡問題的研究首先要考慮的問題,是探索發現實際生活中的一些網絡由于哪些特征才需要,而且可以把它們看作是超網絡問題,以及怎樣建立從概念模型、結構模型乃至于數學模型.現有的超網絡分析優化方法還是極其有限的,需要探尋新的方法.超網絡雖然一時無法得到眾所公認的定義,但是否可以從深人研究其典型特征人手來加以界定.網絡的拓撲結構在網絡的穩定性等方面有著非常重要的作用.

在應用方面,值得考慮的問題是：

a.復雜網絡和超網絡概念的提出,一方面在為客觀事物的描述和建模過程中,填補了離散對象的集總參數模型(利用代數和常微分方程、差分方程)和連續介質對象的分布參數模型(利用數學物理方程)之間的空白(過去像對復雜運輸網絡這類系統的建模是面臨很大困難的).另一方面,提供了考慮和分析網絡各組成部分之間(特別是層間和級間)以及網絡和網絡之間關系的方法.這就為許多復雜系統研究提供了新思路,隨著實際生活中系統的日益復雜和多樣化,將有更多的系統可按照超網絡來處理.

b.在Nagurney所說的“高于而又超于現存網絡”中所指的現存網絡,是節點對應于空間位置、邊對應于物理連接(如道路、線纜)的網絡,而超乎這樣網絡的則是一些帶有虛擬特點的節點、邊和流,如知識節點、社會關系、價格流等.因此超網絡的概念和處理方法必將在虛實結合的網絡研究中顯示其獨特優勢,得到廣泛應用,特別是基于超圖的超網絡.

c.在解決問題的已有研究基礎上,應該在更廣泛的運輸網絡、通信網絡、能源網絡、金融網絡中,考慮更多的風險和其它因素,將超網絡模型進一步完善,使之更符合現實.

d.將超網絡進一步應用于物聯網系統、知識管理系統[11]等一些新型系統之中.

[1] WATTSD J,STROGATESSH.Collective dynamics of“small-world”networks[J].Nature,1998,393： 440-442.

[2] ALBERT R,BARABASI A L,Statistical mechanics of complex networks[J].Review of Modern Physics, 2002,74：47-97.

[3] BARABASI A L,Linked：How Everything Is Connected to Everything Else and What It Means for Science, Business and Everyday Life[M].Cambridge：Perseus Publishing,Inc,2002.

[4] NAGURNEY A,DONG J.Supernetworks：Decision-Making for the Information Age[M].Cheotenham： Edward Elgar Publishers,2002.

[5] NAGURNEY A,WAKOLBINGER T.Supernetworks： An introduction to the concept and its applications with a specific focus on knowledge supernetworks[J]. International Journal of Knowledge Culture and Change Management,2005,4：1-16.

[6] EMESTO ESTRAD A,JUAN A.Rodriguez-velazquez. subgraph centrality and clustering in complex hypernetworks[J].Physica A,2006,364：581-594.

[7] RAMADAN E,TARAFDAR A,POTHEN A.A hypergraph model for the yeast protein complex network[C]∥IPDPS Workshop on High-Performance Computational Biology.Proceedings of the HICOMB 2004.New Mexico：Santa Fe NM,2004.

[8] PIMM S L.Food Webs[M].London：Chapman& Hall,1982.

[9] COHEN J E.Interval graphs and food webs,a finding and a problem.Document 17696-PR[Z].Santa Monica：RAND CORP,1968.

[10] SONNTAG M,TEICHERT H M.Competition hypergraphs[J].Discrete Appl Math,2004,143：324-329.

[11] 王志平,王眾托.超網絡理論及其應用[M].北京：科學出版社,2008.

[12] BERGE C.Graphs and Hypergraphs[M].New York： Elsevier,1973.

[13] BERGE C.Hypergraphs：The Theory of Finite Sets [M].Amsterdam：Elsevier Science,1989.

[14] 羅靜,毛其智,黨安榮.基于超圖的生態環境修復模型的研究與應用[J].計算機工程與應用,2007,43(31)： 188-191.

[15] KARONSKI M.A review of random graphs[J].Journal of Graph Theory,1982,6(4)：349-389.

[16] ARIEZRI S,FRACNKDL E.A deletions game on hypergraph[J].Discrete Applied Mathematics,1991,30： 155-162.

[17] ENDRE BOROS(USA),On shift stable hypergraphs [J].Discrete mathematics,1991,87：81-84.

[18] 黃汝激.超網絡的有向k超樹分析法[J].電子科學學刊,1987,19(3)：244-255.

[19] 貝爾熱C.超圖-有限集的組合學[M].卜月華,張克民譯.南京：東南大學出版社,2002.

[20] TUAN N D.Hypergraphical t-designs[J].Discrete Mathematics,2006,306：1189-1197.

[21] 黃汝激.應用超圖理論實現有向基本割集矩陣[J].電子科學學刊,1992,14(1)：50-60.

[22] HU T C,MOERDER K.超圖中的多端流[C]∥圖論應用新進展,北京：中國電子學會,1989：235-245.

[23] ROSERNBERG A.A hypergraph model for fault-tolerant VLSI processor arrays[J].IEEE Transaction, Computer,1985,C-34(6)：578-584.

[24] 陳廷槐.超圖的連通性和容錯多總線系統的設計[J].中國科學A,1990(11)：1309-1319.

[25] 高則年.具有最佳連通性的超圖和容錯總線系統的設計[J].計算機學報,1990(11)：878-881.

[26] KAMIDOI Y,WAKABAYASHI S,YOSHIDA N.A fast heuristic algorithm for hypergraph bisection[J].IEEE ISCAS,1991(2)：1160-1163.

[27] 郝忠孝.一種基于超圖的最小覆蓋集求法[M].計算機研究與發展,1990(10)：58-64.

[28] WAI YIN MOK,EMBLEY D W.Generating compact redundancy-free XML documents from conceptualmodel hypergraphs[J].IEEE Transactions on Knowledge&Data Engineering,2006(18)：1082-1096.

[29] KARYPISG.Multilevel hypergraph partitioning：Applications in VLSI domain[J].IEEE Transactions on Very Large Scale Integration Systems,1999(7)： 69-70.

[30] BRETTOA,GILLIBERT L.Hypergraph-based imagerepresentation[J].Lecture Notes in Computer Science,2005,3435(135)：1-11.

[31] ALAIN B,HOCINE C,DRISS A.Hypergraph Imaging an overview[J].Pattern Recongition,2002(35)：651-658.

[32] CHASTEL S,COLANTONI P.Displaying image neighborhood hypergraphs line-graphs[J].Lecture Notes in Computer Science,2002(2301)：124-135.

[33] SARKAL S,KUMARN.Hypergraph models for cellular mobile communications systems[J].IEEE Transactions on Vehicular Technology,1998(47)：460-471.

[34] HAN E-H(Sam),GEORGE K.Research Issue on Data Mining and Knowledge Discovery[M].Navi Mumbai：Bioinfo Publications,1997.

[35] OZDAL M,AYKANAT C.Hypergraph models and algorithms for date-pattern-based clustering[J].Data mining and Knowledge Discovery,2004(9)：29-57.

[36] ELENA V K,VLADIMIR A S.Application of hypergraph theory in chemistry[J].Discrete Mathematics, 2001,235：365-383.

[37] SEGOVIA-JUAREZ J L,COLOMBANO S,KIRSCHNER D.Identifying DNA splice sites using hypernetworks with artificial molecular evolution[J].Bio-Systems,2007,87：117-124.

[38] MAO C,YOKOMORI T.DNA hypernetworks for information storage and retrieval[J].DNA12,LNCS,2006, 4287：298-307.

[39] KIM J K,ZHANG B T.Evolving hypernetworks for pattern classificatIon[C]//IEEE Congress on Evolutionary Computation(CEC),Singapore：2007：1856 -1862.

[40] BECKMAN M J.Economic models of knowledge networks[C]∥BATTEN D,CASTI J.Networks Action. Berlin：Springer-Verlag,1995：159-174.

[41] MAGUITMAN A G.Intelligent support for knowledge capture and constructioon[D].Indianapolis：Indiana U-niversity,USA,2004.

[42] BARABASI A L.Virtual round table on ten leading questions for network research[J].European Physical Journal B,2004,38(2)： 143-145.

作者介紹

王眾托中國工程院院士,系統工程與管理工程專家.1951年畢業于清華大學電機系.曾任大連理工大學管理學院院長、中國系統工程學會副理事長.現任大連理工大學教授、知識科學與技術研究中心主任.20世紀50年代至60年代,從事自動化專業建設、自動控制理論與計算機應用方面的學科引進和研究,長期從事教材的編寫與組織,做過許多艱苦的開拓工作.曾研究開發過我國自主研制的石油管卷管機的自動控制系統,以及我國第一臺電渣重熔的交流控制系統.70年代后期開始從事系統工程專業與學位建設,是我國系統工程研究生教育與學科創建人之一.在學科創建初期就開展網絡計劃技術的新方法(決策關鍵路線法)與應用、基于虛擬裝置的煉油企業生產計劃與調度系統分析、元決策理論與應用、智能型交互式集成化決策支持系統等研究,取得顯著經濟效益.曾在維也納國際應用系統分析研究所(IIASA)任研究員,主持國際合作項目,最早開發了用于宏觀經濟發展研究的智能型交互式集成化決策支持系統,開我國決策支持系統研究之先河.曾獲國家級獎勵兩項,部委級獎勵6項.撰寫出版14種教材與專著,翻譯9種經典著作和教材.在國內外發表140余篇學術論文與科學報告.現從事所倡導的知識系統工程研究與應用.

Reflection on supernetwor k

WANGZhong-tuo
(Institute of Systems Engineering,Dalian University of Technology,Dalian 116085,China)

In this paper,the concept of hypernetwork based on hypergraph suggested by C.Berge as another kind of supernetwork is introduced.The main feature of hypernetwork is the edge in hypergraph can be connected to more than one nodes.For the investigation of some complex network like telecommunication network,knowledge network,social network,this unique feature may offer more advantages.

complex work;hypernetwork;hypergraph

N 94

A

1007-6735(2011)03-0229-09

2011-06-07

王眾托(1928-),男,中國工程院院士.研究方向：系統工程、知識科學與技術、決策分析. E-mail：wangzt@dlut.edu.cn