德昌水牛母牛體重體尺的相關性與回歸分析

孟慶輝，柳 茜，盧烈祥 ，敖學成

（1.四川省德昌縣畜牧局，四川 德昌 615500；2.四川省涼山州畜科所，四川 西昌 615042）

1 材料與方法

1.1 分析材料 將2009年德昌縣畜牧局采用普調全縣水牛主產鄉鎮所抽樣的約1歲生長母牛，按統一測定方法分別測得體高、體斜長、胸圍、管圍和體重等相關數據，以此作為分析研究材料。

1.2 統計分析方法 設體重為依變量（y），設其他性狀——體高（x1）、體斜長（x2）、胸圍（x3）、管圍（x4）為自變量，選用Excel和SPSS軟件的相關分析程序完成數據的統計處理。

2 分析與結果

2.1 體重與體尺的相關分析 按相關系數（R）計算公式作相關分析：

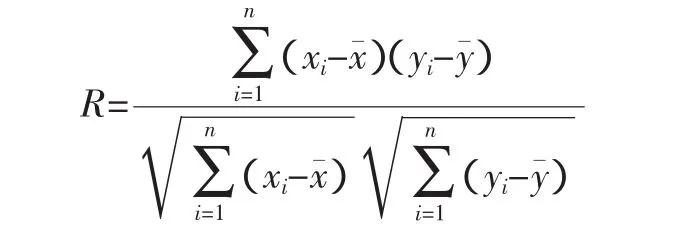
分析結果列于表1。從表1可以看出，體高、體斜長、胸圍、管圍與體重之間的直接相關系數yx1=0.5694**，yx2=0.5788**，yx3=0.9204**，yx4=0.2434；自變量間相關系數除yx2x4為負相關外，其余為正相關，其中達到顯著水平的相關系數yx1x2=0.4565**，yx1x3=0.4597**。因此可以看出體高、體斜長、胸圍與體重較密切相關。

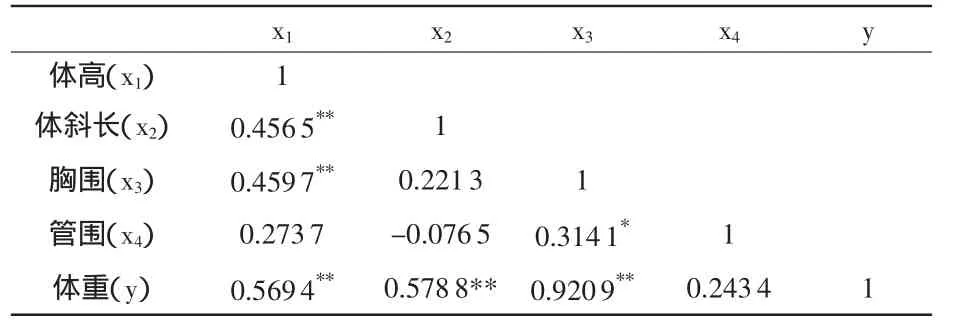
表1 體重與體尺相關系數

2.2 回歸分析

2.2.1 回歸模型的建立 經回歸分析列出回歸系數，見表2。依據表中系數可建立第一個回歸模型，體重 （y）=-746.251+6.221×體重+262.371×體斜長+429.436×胸圍+0.371×管圍。經t值顯著性檢驗，體高、管圍差異不顯著，應削除，再用體重（y）、胸圍（x3）、體斜長（x2）進行第二次回歸分析，得到模型的回歸系數，按此建立第二個回歸模型，體重（y）=-737.381+432.773×胸圍+262.598×體斜長。

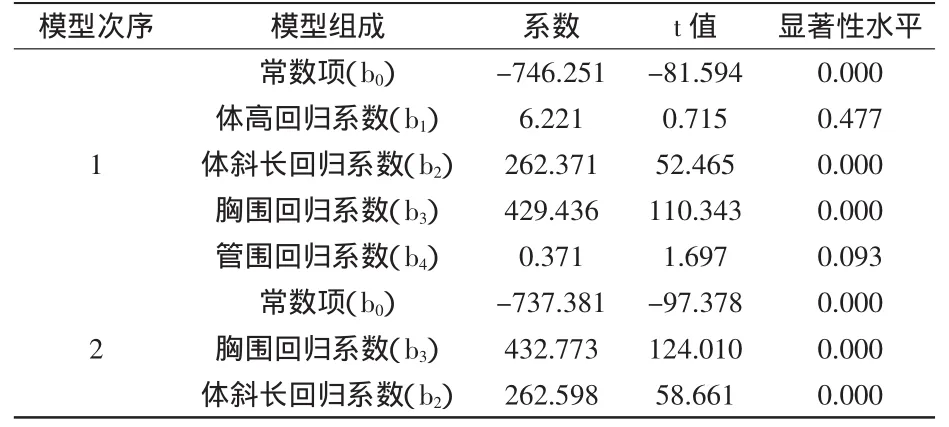
表2 回歸模型系數

2.2.2 回歸模型擬合優度 分析結果列于表3，從表3可看出，用實測值估測回歸模型間的相關系數均為0.998，擬合優度和調整后的擬合優度均為0.996，僅標準差略有差異，表明擬合模型與實際相關程度，吻合性很好。另外從分析輸出實測值標準殘差與估測標準殘差正態分布圖中可觀察到，標準殘差的分布是接近正態分布的，其散點近似一條直線，且與對角線近似重疊，表明兩個回歸模型相似性強。因此可以認定，采用所建回歸模型來估測德昌水牛母牛生長期的體尺、體重是可行的。

表3 模型相關系數與擬合優度

2.2.3 回歸模型的顯著性檢驗 顯著性檢驗分析結果列于表4。從表4可以看出，兩個回歸模型中回歸系數的F值分別為5934.572和11 586.798，其差異極顯著（P＜0.01）；另外，兩個回歸模型的殘差項與均方值相近似，綜合表明兩個回歸模型是與實際相吻合的，具有合理性。

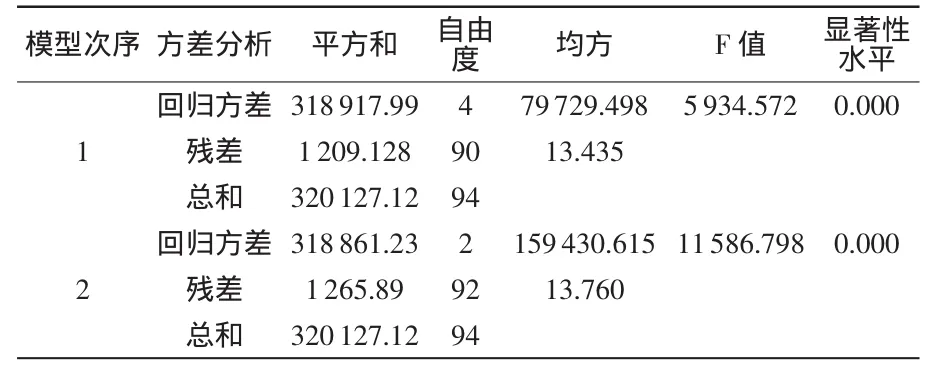
表4 回歸模型的顯著性檢驗

3 分析與結論

3.1 該測定分析的資料抽樣代表性較廣，樣本數量也較大，因此研究結果有一定的參考應用價值。

3.2 該分析從性狀相關分析入手，再經逐步回歸分析法分析，較充分地考察了性狀的相關一致性。在獲得所測性狀的第一個回歸方程基礎上，經篩選削除不顯著體高和管圍性狀，再建立第二個回歸方程，兩個方程的R值和擬合優度值相似，從應用的方便角度看，可首先選用第二個回歸方程，即：體重（y）=-737.381+432.772×胸圍+262.598×體長。

3.3 該分析樣本處于生長期，因此對早期考察德昌水牛的生長發育有價值，可為早期選培工作提供依據。

[1]高祥寶.數據分析與SPSS應用[M].北京：清華大學出版社，2007.

[2]王占紅.復州牛成年母牛體重與體尺指標的相關與回歸分析[J].中國牛業科學，2006，（6）：28-30.

[3]粘 鋒.應用多元回歸原理預測西門塔爾初產母牛305 天產奶量[J].黃牛雜志，2002，（5）：15-16.

[4]蓋鈞益.試驗統計方法[M].北京：中國農業出版社，2009.

[5]石素珍.魯西黃牛背截面指標為參數的胴體產肉率回歸分析[J].黃牛雜志，1999，（2）：30-35.