動態數據驅動的林火蔓延模型模擬誤差自適應修正1)

楊廣斌 唐小明 李亦秋

(貴州師范大學，貴陽，550001) (中國林業科學研究院資源信息所) (綿陽師范學院)

森林火災是一個非常復雜的現象，對森林火災這樣復雜系統行為的精確分析和預測是非常困難的。而林火預防和撲救的時效性很強，森林火災一旦發生，就必須根據影響林火行為的各項因素，確定林火蔓延的趨勢，實時有效地預測、模擬林火行為，以便科學、及時地做出林火指揮撲救決策。因此，運用計算機實現林火的蔓延模擬成為必然，這也是當前林火蔓延研究的一個主要方向。盡管先進虛擬現實技術和元胞自動機模型的發展使得現階段林火模擬在視覺效果和空間擴散方面取得了很大進步，但仍然缺乏對林火蔓延系統的精確描述能力，這種情況在實時動態條件下顯得更為突出［1－4］。美國自然科學基金會(NSF)在2000年首先提出了動態數據驅動應用系統(DDDAS，Dynamic Data Driven Application Systems)的研究概念，并推動和資助了多個相關領域的一系列前瞻性研究，其中動態數據驅動的林火蔓延模擬研究項目受到了多個領域專家的推崇［5－7］。

在我國林火模擬研究中，已采用的林火蔓延模型主要有Rothermel模型及王正非的林火蔓延模型［8－9］。林火蔓延模型是建立在一定范圍內的模型，都有局限性。對于一個地區的林火蔓延模擬，可以選擇適宜的已有林火蔓延模型，再根據本地實際情況對模型進行修正。傳統的模型修正方法是通過多次點火試驗來確定模型的修正參數。這種模型修正方法不僅周期長、效率低，而且一旦模擬環境有較大變化時，修正的參數就不再適用。文中以動態數據驅動技術為基礎，通過對模擬精度驗證方法和模擬誤差的分析，確定模擬誤差修正參數及其計算方法，通過神經網絡技術實現模擬誤差修正參數自動生成過程，并對模擬誤差修正效果進行試驗和分析。實現了林火模型的在線自適應修正，從而提高林火蔓延模擬的精確性和時效性。在實踐上為林火撲救指揮提供決策支持，在理論上為相關領域的空間擴散模擬研究提供新的思路和技術范式。

1 林火蔓延模擬誤差分析

在林火模擬過程中，模擬的林火蔓延與真實的林火蔓延之間只能是最大程度的相近，不可避免地存在模擬的林火蔓延與真實林火蔓延之間的誤差問題。

1.1 誤差來源

在林火蔓延模擬過程中，誤差的來源包括數據誤差、模型誤差、不同算法和各種測量儀器產生的誤差等。

數據誤差:包括野外動態氣象數據誤差、地形數據誤差、可燃物數據誤差等。

模型誤差:林火模型是對實際林火蔓延過程的一種抽象表達，簡單的林火蔓延方程不可能把復雜的林火蔓延過程十分準確地表達出來。

算法誤差:從動態數據的采集到林火蔓延模擬的實現，涉及許多技術實現的算法，如氣象數據插值算法、林火蔓延空間擴散算法等，這些算法會對模擬結果直接或間接地產生影響。

儀器和設備誤差:GPS火場位置數據采集、無線傳輸設備的時間延遲都會對模擬結果造成誤差。

1.2 誤差表現形式

根據林火模擬結果的表現形式不同，誤差主要表現在以下幾個方面:

位置誤差:實際火場某點位置與模擬火場對應點位置之間的差異，可用距離來表示。如實際火場火頭位置點M與模擬火場火頭位置點M＇之間的距離l，即是模擬的火頭位置M的誤差(圖1)。

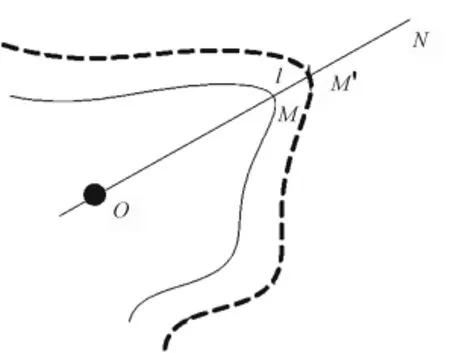
圖1 火場位置誤差

火線長度誤差:實際火線長度與模擬火線長度之差。局部火線長度誤差是指實際火場兩點之間的長度與模擬火場相應兩點之間的火線長度之差(圖2中ANB－A＇N＇B＇);整體火線長度誤差是指整個實際火場火線總長度與模擬火場火線總長度之差(圖2 中ANBM－A＇N＇B＇M＇)。

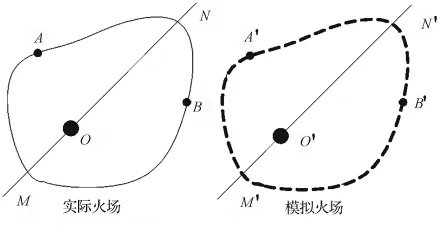
圖2 火線長度誤差

火場面積誤差:實際火場面積與模擬火場面積之差。

火場形狀誤差:實際火場形狀與模擬火場形狀之間的差異，可用形狀變形系數來表示:

式中:K為變形系數，K值越大，表示形狀越規則;A為火場面積;P為火線總長度。

蔓延速度誤差:實際林火蔓延速度與模型計算蔓延速度之差。

蔓延方向誤差:實際林火蔓延方向與模擬林火蔓延方向之間的差異，可用實際火場某點相對于著火點的方位角與模擬火場對應點相對于著火點的方位角之差來表示，圖3中α－β，即為A點的蔓延方向誤差。

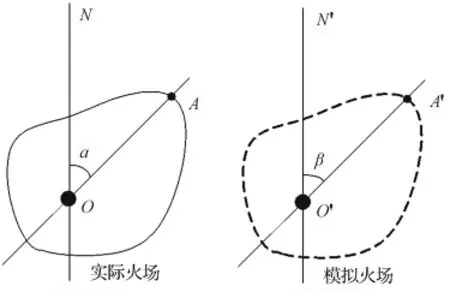
圖3 蔓延方向誤差

1.3 誤差分析

由于林火蔓延的位置、火線長度、火場形狀和火場面積直接由林火蔓延的速度和蔓延方向決定，所以，在上述幾種誤差中，林火蔓延速度誤差和蔓延方向誤差是最基本的誤差，直接決定著其他幾種誤差的大小。林火蔓延方向主要受風向的影響，在復雜地形條件下，風向受地形的影響比較大，因此，通過地形風場模型可減小林火蔓延方向誤差［10－12］。

文中主要探討如何通過減小蔓延速度誤差減小林火蔓延模擬的誤差。

林火蔓延速度誤差是由多種因素共同影響產生的，通過對模型中的每個影響因子進行修正來減小模擬誤差的做法是不現實的。因此，文中通過對模型增加一個全局修正因子，使林火蔓延模擬速度與實際林火蔓延速度相等，從而實現對林火蔓延模擬誤差的修正。

2 模擬誤差自適應修正

人工神經網絡，或稱神經網絡(Neural Networks，簡稱NN)是由大量的、同時也是很簡單的處理單元(或稱神經元)廣泛地互相連接而形成的復雜網絡系統，它反映了人腦功能的許多基本特性，是一個高度復雜的非線性動力學系統。神經網絡具有大規模并行、分布式存儲和處理、自組織、自適應和自學習能力，特別適用于處理需要同時考慮許多因素和條件的、不精確和模糊的信息處理問題［13］。文中基于動態數據驅動技術和神經網絡原理構建林火蔓延模擬誤差在線自適應修正系統，模擬誤差的在線自適應修正就是在動態輸入的火場環境數據驅動作用下，通過林火模擬，根據火場環境數據自動地生成模擬誤差修正參數值，并在模擬過程根據火場精度驗證數據形成學習樣本和進行知識積累的過程。這個過程是一個系統自學習、自適應和自動知識積累的過程(圖4)。

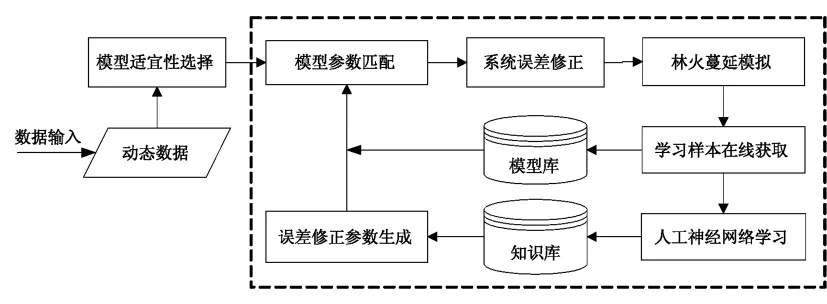
圖4 模擬誤差在線自適應修正過程

2.1 模擬誤差修正參數確定

不同林火蔓延模型，其表達式不同，輸入參數和輸出結果也不相同，即使同一個模型，當模擬環境條件改變時，其參數也隨之改變。林火蔓延模型用一般函數可表示為:

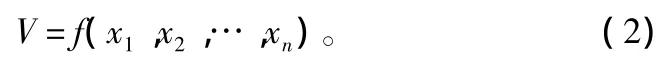
式中:V為林火蔓延模擬速度;x1，x2，…xn為林火蔓延影響因子，如植被、坡度、風力等;n為影響因子個數。

實際林火蔓延速度為R，則R可表示為:

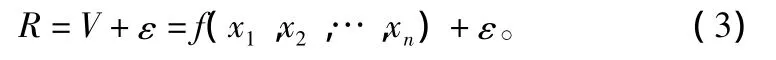
式中，ε為林火蔓延模擬誤差修正參數，則有:

設林火蔓延的最大實際速度為Rmax，則ε的最大取值范圍為:

由以上模擬誤差修正參數推算公式可知，模擬誤差修正參數由實際林火蔓延速度R和林火模型計算速度V之差決定。

林火蔓延的實際速度是通過實時測量方法獲取的。火場環境數據是相應火場實時獲取的火場環境數據。根據火場環境數據和林火蔓延模型可計算出林火蔓延的理論速度，這樣就可以計算出模型的模擬誤差修正參數。

2.2 神經網絡模型構建

反向傳播(BP)網絡就是一種多層前向神經網絡，是目前最常見、應用最廣泛的一種神經網絡。從結構上講，它由輸入層、中間層(隱含層)和輸出層組成，網絡中每個神經元通過求輸入權值和經激活函數傳遞結果來工作，通過改變學習速率、動量因子可以提高BP學習算法的收斂速度［14－15］。文中以王正非模型為基礎，構建林火蔓延模擬誤差修正神經網絡模型。

確定輸入輸出結點:根據火場環境因子和林火蔓延模型參數，確定輸入結點為植被、坡度、風速、氣溫、大氣濕度5個因子，用向量表示為:

X=［植被，坡度，風速，氣溫，大氣濕度］。

輸出結點只有1個，即模擬誤差修正參數。

確定隱含層結點數:隱含層結點數通過輸入層和輸出層結點數來確定，即取輸入輸出層結點數的平均值，因此，隱含層結點數為3。

構建神經網絡結構:建立一個3層的BP神經網絡，網絡結構如圖5所示。

圖5 模擬誤差修正參數預測神經網絡結構

確定作用函數:作用函數為(0，1)S型函數:

學習速率、動量因子和最小期望誤差的確定:學習速率決定每一次循環訓練中所產生的權值變化量。大的學習速率可能導致系統的不穩定;小的學習速率導致較長的訓練時間，可能收斂很慢，但能保證網絡的誤差值不跳出誤差表面的低谷而最終趨于最小誤差點。附加動量使權值的修改增大，合適的動量因子可加快學習過程的收斂速度，但是值過大也會引起學習過程的振蕩，動量的大小尚無定論，通常由試驗確定。

2.3 模擬誤差修正參數獲取

由歷史火場環境數據和火場實際蔓延速度數據，計算生成模擬誤差修正參數。系統在正式運行之前無法自動獲取模型選擇的學習樣本，這就需要利用歷史火場記錄數據作為訓練樣本來形成模型選擇的知識。林火模型本身所帶的參數與計算得到的模擬誤差修正參數是一一對應的，將其進行匹配(圖6)，生成原始學習樣本(表1僅列出部分樣本)。

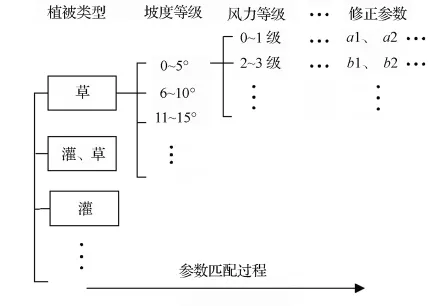
圖6 模型參數匹配框架結構及匹配過程

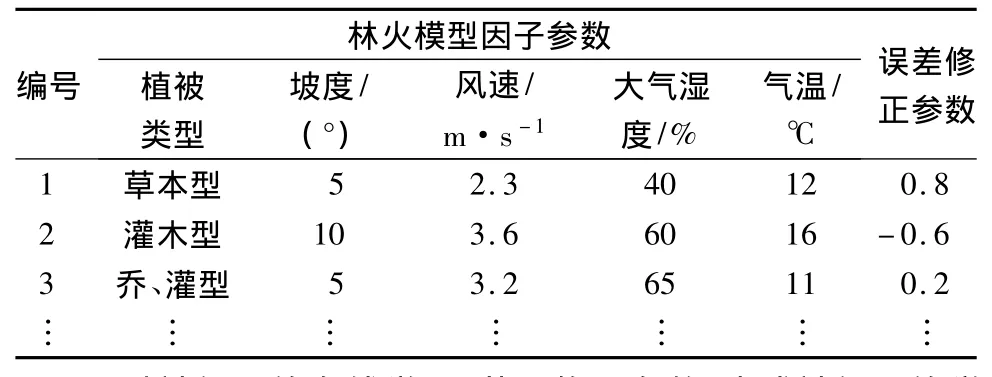
表1 原始學習樣本

通過神經網絡在線學習，獲取修正參數，生成神經網絡學習樣本。歷史數據獲取誤差修正參數是有限的，需要通過神經網絡學習，生成新的學習樣本。在火場動態數據的驅動下，網絡學習樣本是在林火模擬過程中自動產生的，其生成過程如圖7所示。

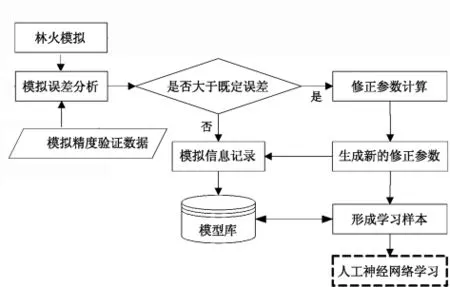
圖7 網絡學習樣本在線獲取過程

通過以上2種方式獲取到的模擬誤差修正參數精度是不同的，從歷史數據獲取的參數與火場環境是一一對應的關系，也是經過實際測量數據驗證的，具有較高的精度，不需要經過再修正。而由神經網絡預測自動生成的誤差修正參數，它只是一個預測值，或者說是估算值，是經過知識推理產生的，它的精度依賴于神經網絡先前學習的樣本精度和樣本數量，與火場環境數據不具有一一對應關系。因此，在模型模擬誤差修正參數匹配時，首先從數據庫中搜索是否有與輸入的火場環境數據相匹配的誤差修正參數，如果有，則直接讀取此參數作為這次模擬的誤差修正參數;如果沒有，則通過神經網絡和知識庫自動生成一個誤差修正參數，用此參數作為模擬的修正參數，如果模擬結果誤差超出預期值，則還要通過驗證數據對此參數進行再修正。

按照上述設計的模擬誤差修正過程，模型模擬誤差修正參數是一個常數，它是對一場林火過程中的某一時間段內的林火蔓延速度的修正，并假定在這個時間段內火場環境因子數據是單一的、均勻的、不變的。但是，在實際林火燃燒過程中，火場環境因子是不斷變化的，模型模擬誤差修正參數也是隨著環境的變化而改變的。因此，模型模擬誤差修正參數是一個可變常數，它是隨著火場動態輸入的環境因子的數據變化而改變的，火場每輸入一次數據，模型模擬誤差修正參數就會相應地改變1次。這種模擬誤差的修正即為動態數據驅動的林火蔓延模擬自適應修正。

3 模擬誤差修正試驗

3.1 試驗數據

為了驗證模型修正方法的有效性，文中采用歷史記錄火場數據進行試驗。在1986—2010年北京市歷史火場中，選擇出適宜于王正非模型模擬的96條記錄，作為模擬誤差修正參數自動生成的試驗樣本集，其中80條記錄作為學習樣本，16條記錄作為驗證樣本。選擇火場記錄的原則是:保證比較單一的火場環境，即植被、坡度、風速、氣溫、大氣濕度這些因子值在同一場林火中變化較小;過火面積不宜過大，避免實際火場環境比較復雜，使計算出的林火蔓延速度與實際蔓延速度相差較大。表2為選取的歷史火場記錄。

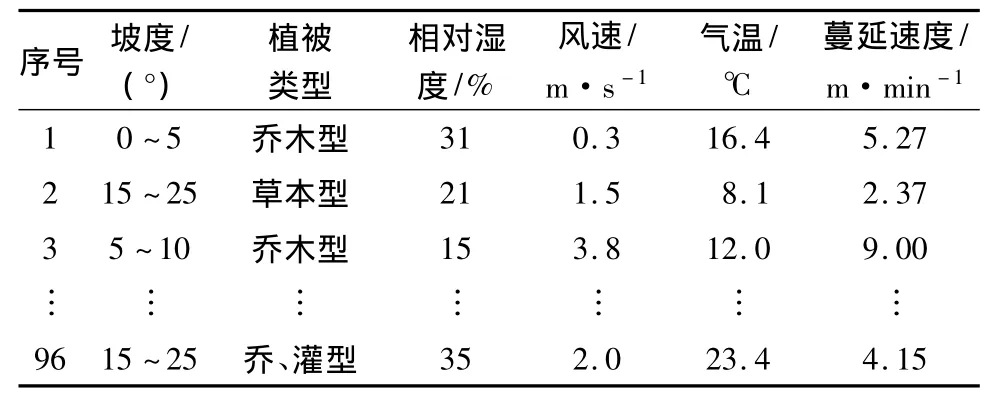
表2 模型模擬的火場數據記錄

3.2 數據標準化處理

由火場采集的數據不能直接作為神經網絡的輸入數據，需要對數據進行標準化處理。在進行神經網絡計算時，為了加快網絡的收斂速度，將數值一般采用［0，1］表示的形式，即對數值進行極值標準化計算。數據標準化處理步驟如下:

對原始數據進行分類或分級，并采用數值形式表示。

坡度分級數值化為:1表示坡度為0°～5°;2表示5°～10°;3表示10°～15°;4 表示15°～25°;5 表示25°以上的坡度。

植被分類數值化為:1表示草本型植被;2表示灌草型植被;3表示灌木型植被;4表示喬灌型植被;5表示喬木型植被。

求平均值。用u1k，u2k，…，uik，…，unk，uik表示第i個樣本對第k項指標取得的數據，i=1，2，…，n，n=12，k=1，2，3，4，5。原始數據平均值:

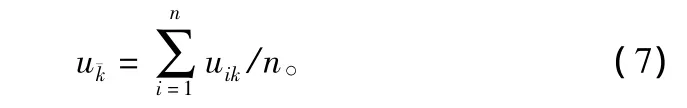
求標準差。原始數據標準差:

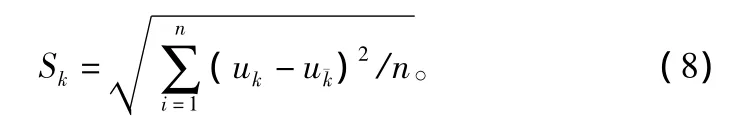
求標準化值。原始數據標準化值:

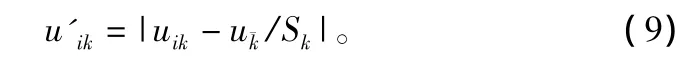
數據極值標準化。采用極值標準化公式計算，得到［0，1］區間的標準化數據:

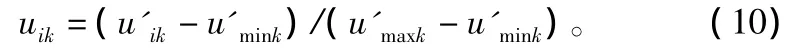
式中:u＇maxk和u＇mink分別表示u＇1k，u＇2k，…，u＇nk中的最大值與最小值。

神經網絡的輸出樣本是根據模擬誤差修正參數計算公式求得的。首先根據火場環境因子、過火面積和著火時間計算出林火蔓延的實際速度，然后把火場環境因子輸入王正非模型中計算出模擬速度，最后求得模型蔓延速度的誤差修正值，此修正值本身是數值型，不需要再進行模式轉換，可直接作為神經網絡的輸出因子值。

3.3 試驗結果

在試驗中，BP網絡的學習速率η=0.3。采用附加動量的權值修正，權值調節的動量因子取α=0.75。網絡實際輸出和目標輸出的最小期望均方誤差定為0.01。當神經網絡訓練次數達到650次時，網絡滿足了預先設定的精度要求。試驗結果形成的網絡權值和閾值為:

式中:W1表示網絡權值矩陣;W2表示網絡權值轉置矩陣:B1表示網絡閾值矩陣:B2表示網絡閾值的轉置矩陣。

3.4 修正效果分析

為了驗證以上網絡學習的效果，將整理好的16場歷史火場記錄作為網絡輸入因子，預測其輸出值。將神經網絡生成的修正參數與計算得出的修正參數進行對比，評估神經網絡的預測精度(表3)。

在以上預測的16條記錄中，其中14條與計算結果誤差小于預定的 0.20 m·min－1，2 條誤差超過0.20 m·min－1，因此，通過試驗可知，模擬誤差修正結果精度具有一定的可靠性。

4 結論與討論

林火蔓延速度誤差和蔓延方向誤差是最基本的誤差，直接決定著其他幾種誤差的大小。地形風場模型可減小林火蔓延方向誤差，文中主要探討通過減小蔓延速度誤差減小林火蔓延模擬的誤差。

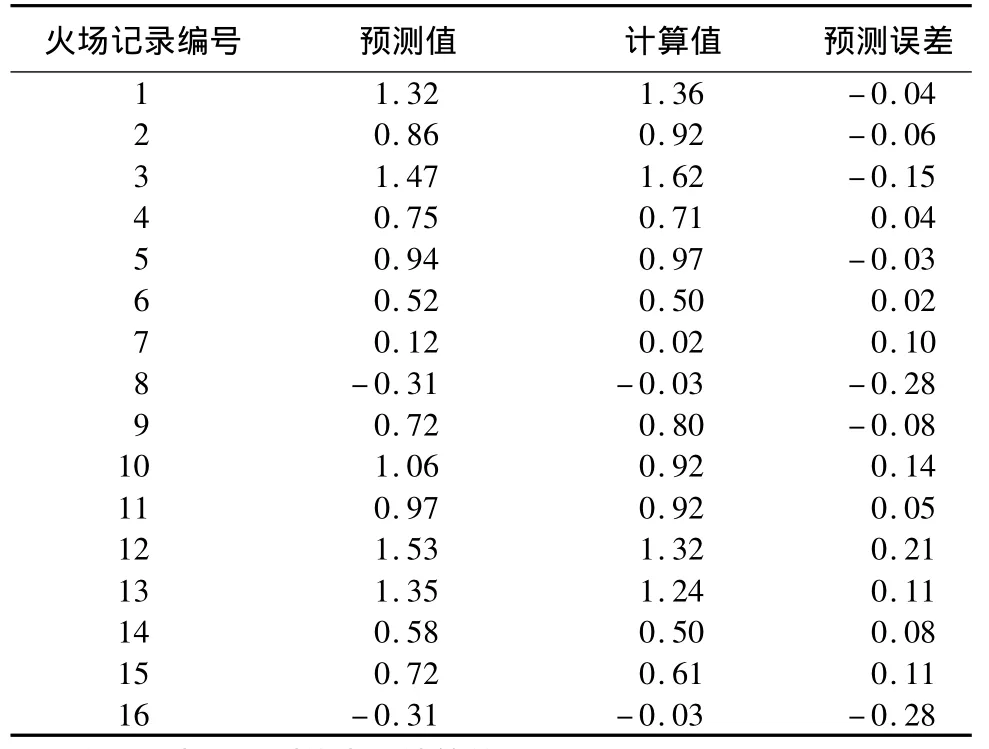
表3 預測值與計算值結果對比 m·min－1

確定了模擬誤差修正參數的計算方法，基于動態數據驅動技術和神經網絡技術構建林火蔓延模擬誤差在線自適應修正系統，探討模擬誤差在線自適應修正機制和模擬誤差修正知識在線自動獲取機制，實現模擬誤差的在線自適應修正過程。

以王正非林火蔓延模型為例，采用歷史記錄火場數據對模擬誤差的自適應修正過程進行了試驗。選擇了96條記錄作為試驗樣本集，其中80條記錄作為學習樣本，16條記錄作為驗證樣本。在預測的16條記錄中，其中14條與計算結果誤差小于預定的 0.20 m·min－1，2條誤差超過 0.20 m·min－1，模型模擬誤差修正達到了較為理想的效果。

基于動態數據驅動和神經網絡技術構建的林火蔓延模擬誤差在線自適應修正系統，提供了火場環境數據和林火蔓延速度數據采集機制，是一個自學習、自適應和自動知識積累的系統，隨著系統的不斷完善和數據、知識的不斷積累，將最終解決林火蔓延模擬數據瓶頸問題，實現林火蔓延模擬與真實的林火蔓延之間最大程度的相近。

［1］田勇臣，劉少剛，趙剛，等.森林火災蔓延多模型預測系統研究［J］.北京林業大學學報，2007，29(4):49 －53.

［2］McDonough J M，Yang T.Parallel performance of a new model for wildland fire spread predictions，paralle CFD(Computational Fluid Dynamics)Conference［J］.Las Palmas de Gran Canaria(ES)，2004(5):45－51.

［3］Trunfio G A.Predicting wildfire spreading through a hexagonal cellular automata model［J］.Lecture Notes in Computer Science，2004，33(5):385 －394.

［4］黃華國，張曉麗，王蕾.基于三維曲面元胞自動機模型的林火蔓延模擬［J］.北京林業大學學報，2005，27(3):94 －98.

［5］Ouyang Ying，Zhang Jiaen，Luo Shiming.Dynamic data driven application system:Recent development and future perspective［J］.Ecological Modelling，2007，204(1/2):1 －8.

［6］Pidd M.Guidelines for the design of data driven generic simulators for specific domains［J］.Simulation，1992，59(4):237 －243.

［7］Mosterman P J，Sztipanovits J，Engell S.Computer－automated multiparadigm modeling in control systems technology［J］.IEEE Transactions on Control Systems Technology，2004，12(2):223 －234.

［8］唐曉燕，孟憲宇，易浩若.林火蔓延模型及蔓延模擬的研究進展［J］.北京林業大學學報，2002，24(1):87 －91.

［9］Richards G D.A general mathematical framework for modeling twodimensional wildland fire spread［J］.International Journal of Wildland Fire，1995，5(2):63 －72.

［10］Feliks Y，Gavze E，Givati R.Optional vector interpolation of wind fields［J］.Journal of Applied Meteorology，1996，35:1153 －1158.

［11］桑建國，溫市耕.大氣擴散的數值計算［M］.北京:氣象出版社，1992:35－38.

［12］余琦，劉原中.復雜地形上的風場內插方法［J］.輻射防護，2001，21(4):213 －218.

［13］田曉瑞，舒立福，王明玉，等.西藏森林火災時空分布規律研究［J］.火災科學，2007，16(1):10 －14.

［14］侯彥東，方惠敏，楊國勝，等.一種改進的可變學習速率的BP神經網絡算法［J］.河南大學學報:自然科學版，2008，38(3):301－312.

［15］張會生，吳微.一種具有自適應動量因子的BP算法［J］.大連海事大學學報，2008，34(4):45 －51.