多重分形理論在原木圖像處理中的應用1)

韓書霞 戚大偉

(東北林業大學，哈爾濱，150040)

采用計算機斷層掃描技術(CT)對原木進行無損檢測，對取得的缺陷圖像采用分形理論進行圖像處理，目前國內外已有很多學者在研究［1］，這些研究從分形理論的分形維數方面已取得了非常可喜的成果。但對多重分形頻譜的選擇卻各有不同。本文通過采用多重分形三種頻譜fh(α)、fg(α)、fl(α)的選擇，對原木缺陷CT圖像進行了處理，找到了一種新的準確確定原木內部缺陷邊緣的方法。

1 多重分形分析理論與圖像分析

1.1 多重分形理論簡介

多重分形也稱為標度分形或復分形。常用來表示一個整體特征標度指數(分形維數)所不能完全描述的奇異性幾率分布，它是從信號的局部特征出發來研究其特征。多重分形分析的目的在于量化測度的奇異結構，以及在尺度發生變化時為伴隨有不同范圍的冪定律的現象提供模型［2］，尤其適用于一些難以建模的不規則圖像處理和分析。由于多重分形分析具有良好的局部性和全局性，因此為圖像的邊緣檢測提供了一種新的途徑。

1.2 H?lder指數的應用

設f(x)為f:R→R的函數，如果有∣f(x)－P(x－x0)∣＜C∣x－x0∣α，其中:α＞0，P為不超過 α 的多項式，x∈B(x0，δ)得閉球，C為一大于0的常數，令

α(x0)=sup(α:f∈Cαx0);

α(x)=sup(α:f∈Cαx)。

則稱α(x0)為函數f(x)在x0點的 H?lder指數，α(x)為f(x)在其定義域上的H?lder指數［3］，α是表征分形體某小區域的分維，稱為局部分維。因此H?lder指數α能夠很好地描述函數f(x)的局部特性。

1.3 多重分形頻譜與圖像分析

1.3.1 Hausdorff頻譜

多重分形用H?lder指數α表示分形體小區域的分維，由于小區域的數目很大，于是可得一個由不同α所組成的無窮序列構成的譜f(α)，f(α)又稱為奇異譜。

設Eα為 H?lder指數 α的點集，如果令fh(α)=dimh(Eα)，其中 dimh為的 Hausdorff維，那么稱fh(α)為Eα的Hausdorff頻譜，因此Hausdorff頻譜能夠很好地描述點集Eα的全局。

多重分形圖像分析過程，首先選擇一容量序列vn及參考測度μ［4］，計算出圖像的H?lder指數α(x)和多重分形頻譜fh(α(x));然后根據(α(x)，fh(α(x)))的值用幾何和概率的方法對圖像的每個像素點進行分類和處理。因此，判斷某一像素點是否為邊緣，既取決于局部特征，又要考慮到圖像的整體性。

1.3.2 粗粒化頻譜和離差頻譜

當n∈N，ε＞0，令

N(α)=，其中#()表示集合中元素的數目設為α的粗粒化頻譜和離差頻譜。

1.3.3 Legendre 頻譜

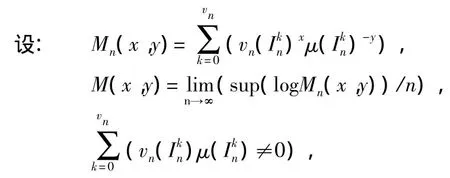
則存在一個凹函數τ，使得

設τ*為τ的Legendre多重分形頻譜，則τ的Legendre變換為fl(α)= τ*(α)=infq［qα－τ(q)］，稱fl(α)為 α 的 Legendre頻譜［5］。

1.4 多重分形頻譜的選擇

多重分形理論的中心問題是三種頻譜fh(α)、fg(α)、fl(α)的選擇，由以上分析可以看出fl(α)的計算最為簡單，但會導致信息的丟失;fg(α)要逐點計算，使奇異點分布的概率描述，能夠很好的反映出頻譜的細節信息;fh(α)對應于Hausdorff維，是奇異點的幾何描述，計算比較復雜。在某些特定的情況下fh(α)=fg(α)=fl(α)，定為f(α)，但三者之間一般滿足fh(α)≥fg(α)≥fl(α)的關系［3－4］。

根據多重分形理論及上述分析可得到:①一般說來，粗糙區域的點的規律性較低，需要找到可以與輪廓線區分的方法，如果與某點的H?lder指數相應的多重分形頻譜的數值為f(α)=1，則該點一定在輪廓上。②邊緣上的點除了有幾何學的特征外，還存在統計學特征:當一個像素點是一個分辨率的圖像中任意選定的，通過它被找到的概率可以判斷其是否為邊緣上的點。例:若頻譜f(α)=1時，可以篩選出邊緣點;若頻譜f(α)=1.5時，可以得到不規則的輪廓線;若頻譜f(α)接近2時，可以獲得光滑區域或粗糙區域的信息［6］。

1.5 圖像的多重分形邊緣檢測方法

根據所得出的多重分形頻譜，可以將圖像的像素點進行分類，若像素點的多重分形頻譜f(α)=1.0，則此像素點為平滑邊緣點;若f(α)=t(1.0＜t＜2.0)，則稱該像素點為t類邊緣平滑點。平滑邊緣點和奇異邊緣點就構成所檢測圖像的邊緣。

2 方法驗證

用計算機斷層掃描技術(CT)對木材進行缺陷檢測，實驗所用的圖像為原木CT腐朽圖像(見圖1)。圖2～圖4分別為多重分形頻譜f(α)=1.0、1.0≤f(α)≤1.1、1.2≤f(α)≤1.3邊緣檢測結果。從圖2～圖4可以看出，只要選擇適當的多重分形頻譜閾值f(α)的值，使用多重分形頻譜分析的邊緣檢測方法能夠測出比較精細的邊緣，且閾值f(α)的范圍增大，檢測出的邊緣就更精確。

圖1 原木CT腐朽原圖像

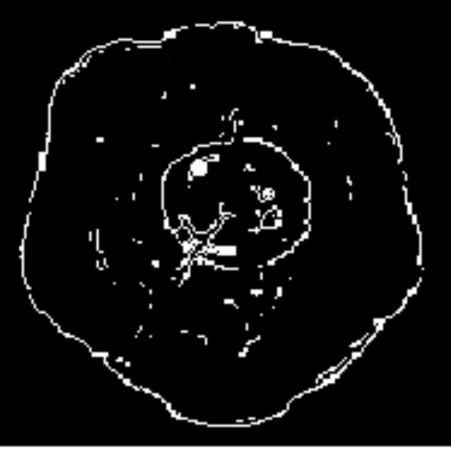
圖2 f(α)=1.0邊緣檢測結果

3 結束語

通過實驗證實，基于多重分形頻譜分析進行的木材CT圖像的邊緣檢測是有效的，優點是:該方法首先計算圖像各像素點的H?lder指數α(x，y)，然后估計出其多重分形頻譜f(α)的值，最后對圖像的像素點進行分類;同時從實驗的結果可以看出，多重分形頻譜的選擇直接影響邊緣檢測的結果，選擇適當的頻譜閾值，可以得到更多的邊緣細節;該方法對于圖像邊緣檢測也具有良好的局部性。因此，多重分形頻譜分析為木材CT圖像邊緣檢測提供了一種新方法。

圖3 1.0≤f(α)≤1.1 邊緣檢測結果

圖4 1.2≤f(α)≤1.3 邊緣檢測結果

［1］Qi Dawei，Yu Lei，Han Shuxia，et al.Based on computed tomography multifractal analysis of wood defect［C］//IEEE International Conference on Control and Automation.Guangzhou，China:IEEE International Conference on Control and Automation，May 30 to June 1，2007:336－341.

［2］肯尼思·法爾科內.分形幾何中的技巧［M］.曾文曲，王向陽，陸夷，譯.沈陽:東北大學出版社，1999.

［3］王耀南，王紹源.基于多重分形頻譜分析的圖像邊緣檢測［J］.湖南大學學報:自然科學版，2004，31(4):28－33.

［4］Lévy Véhel J，VOJAKR.Multifractal analysis of choquet capacities:preliminary result［J］.Adv Appl Math，1998，20(1):1－43.

［5］戚大偉.基于分形理論的原木缺陷圖像處理［M］.哈爾濱:哈爾濱地圖出版社，2004.

［6］Canus C.Robust large deviation multifractal spectrum estimation［M］.Tangier:Proceedings of International Wavelets Conference，1998:739－740.