基于小波分析的信號去噪方法

劉志松

（浙江海洋學院數理與信息學院，浙江舟山 316004）

1910年Haar構造了緊支撐Haar函數系，但是直到80年代人們才真正開始研究小波，1986年，Mallat和Meyer提出了多分辨分析理論（Multi-resolution Analysis，簡記MRA），為小波的構造提供了一般的途徑。多分辨分析的思想是小波分析的核心，是理論和應用的結晶。從此，小波分析真正形成為一門學科，由于其數學的完美性和應用的廣泛性，使其在科學應用上得到了迅速發展，它是調和分析發展史上里程碑式的進展。

長期以來，傳統的Fourier變換在信號分析、處理中起了十分重要的作用，也是信號去噪的主要手段。但是給信號去噪的同時，存在著保護信號和抑制噪聲之間的矛盾。而且在實際應用中，大多數信號都是非平穩的，這給Fourier變換對非平穩信號去噪帶來了困難。近年來，小波理論得到了迅速的發展，由于其良好的時頻特性在信號去噪領域受到了許多學者的重視。

1 傳統信號去噪方法和去噪性能指標介紹

在實際工程問題中，我們得到的原始信號總會混雜著一定的噪聲，而噪聲的存在嚴重地干擾了信號的本質特征。因此，在對原始信號進行預處理時，對噪聲加以消除或減小，以便最大程度的提取原始信號中的有用信息，是非常必要的。

在實際問題中，信號去噪性能好壞有許多的標準，下面我們介紹三種常用標準：

1)信噪比。信噪比是指信號的功率與噪聲功率的比值，常被用來作為去噪效果評價的指標，信噪比的單位是分貝，去噪后的信噪比越大說明消噪效果越好.

2)信噪比增益。文獻[1]將信噪比增益作為去噪效果的指標，它的定義是去噪后的信噪比與去噪前的信噪比的比值，去噪比增益越大，說明消噪效果越好。

3)均方根誤差。均方根誤差是指原始信號與去噪后的估計信號的均方根。

在信號處理和分析中，通常把信號分為平穩信號和非平穩信號。信號的噪聲一般集中在高頻，而有用信號的頻譜又是主要集中在一個有限的低頻空間里。處理實際問題時，人們總是希望把噪聲減小到可以忽略不計的程度，而使其能完全重構出信號的本來面貌。所以信號去噪有很多的方法，最常用的是Fourier變換方法和基于小波變換的信號去噪方法。

2 基于Fourier變換的信號去噪法

Fourier變換是數學分析中的重要分支，經過近些年的發展，使得它的應用領域得到大大的擴大，現已成為眾多科學領域里重要的應用工具之一。

2.1 Fourier變換

在信號分析中，對信號的基本刻化往往采取兩種最基本的形式，即時域形式和頻域形式。Fourier變換是將信號的時域特征和頻域特征聯系起來，能分別從信號的時域和頻域觀察。設原始信號為f(t)，其Fourier

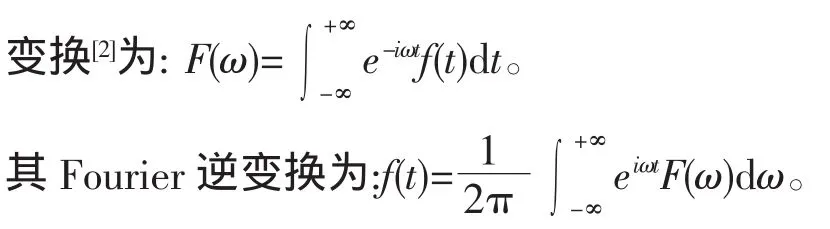
從物理意義上講，Fourier變換的實質是把f(t)這個波形分解成許多不同頻率的正弦波的疊加和，因此Fourier變換在時間域上沒有任何分辨率。這樣在利用Fourier變換做信號分析時就面臨著一對矛盾:時域和頻域的局部化矛盾。在實際信號處理中，尤其是在對非平穩信號的處理中，信號在任一時刻附近的頻率特征都很重要，這促使我們尋求中能將時域和頻域結合起來描述和觀察信號的方法。

2.2 窗口Fourier變換

為了克服標準Fourier變換在時頻局部化的不足，Dennis Gabor于1946年引入了窗口Fourier變換。窗口Fourier變換雖具有一定的局部分析能力，但它的窗口是確定的，不能改變的，它只具有單分辨率的分析，對平穩信號有一定的分析能力，但對于非平穩信號它無法根據信號的變化情況來調整時頻分辨率。

3 小波分析的信號去噪及其仿真實現

近年來，利用小波變換進行信號去噪始終是一個熱門課題。小波分析作為一種全新的信號處理方法，它將信號中各種不同的頻率成分分解到互不重疊的頻帶上，為信號濾波、信噪分離和特征提取提供了有效途徑，特別在信號去噪方面顯出了獨特的優勢。

3.1 小波分析理論介紹

小波分析是Fourier分析思想方法的發展和延拓，能同時在時域和頻域內進行局部化信號分析。是一種優于Fourier變換和窗口Fourier變換的信號處理方法，現在已經迅速發展成一門新興的學科。

小波變換[3]是一種信號的時間-頻率分析方法，它具有多分辨率分析的特點，而且在時頻兩域都具有表征信號局部特征的能力，小波分析的這種特性被譽為數學的顯微鏡。小波變換將信號分解為一系列由某個母小波函數經過平移與尺度變化得到的小波函數的疊加，用不同尺度小波對同一信號進行逼近有利于對信號進行逐步細致的分析，這是小波分析的基本思想。它的這種特性，使小波變換具有對信號的自適應性，這決定了小波變換對非平穩信號進行時頻分析時所具有的時頻局部化的能力。

設ψ(t)∈L（2R）是平方可積即能量有限的信號，當其Fourier變換滿足允許條件時，我們稱它為一個母小波。將母函數ψ(t)經伸縮和平移后，就可以得到一組小波基函數。對母小波進行縮放和平移操作，進而計算信號在小波分解下的系數，所得系數代表著小波和局部信號間的相互關系。小波分析分為連續小波變換和離散小波變換，在實際信號處理中，我們通常使用二進制離散小波序列

3.2 含噪信號的小波去噪原理及步驟

原始輸入信號S通過2個互補的濾波器產生低頻A和高頻D 2個信號，對大多數信號來說，低頻部分是最重要的，基本體現了信號的特征，而高頻部分是信號的細節部分，與信號噪聲聯系在一起。小波分解是將信號的低頻部分反復分解，而對高頻部分不做第二次分解，只對低頻做第二次分解，反復分解低頻部分，這樣就得到小波分解樹。例如對信號S的分解如圖1所示。

信號以三層分解來進行說明:S=A1+D1=A2+D2+D1=A3+D3+D2+D1.如果要進一步的分解，則可以把信號分解的低頻部分A3分解成低頻A4和高頻D4，以下再分解依此類推。但是在實際應用中，對信號的分解不是任意的，而是可以選擇合適的分解層數。從圖1可以看出，對低頻部分進行進一步的分解，使頻率的分解率變得越來越高。基于小波的信號去噪問題在數學上是一個函數逼近的問題，從信號處理的角度來看，小波去噪問題就是一個信號濾波問題，小波去噪實際上是特征提取和低通濾波的綜合，所以還成功地保留原有真實信號的特征信息。

在實際中，通常有用信號的基本特性都集中在低頻部分，信號細節部分和噪聲通常都表現在高頻部分，因此我們要進行小波消噪有三個步驟:

1)選擇一個小波并決定小波分解層次N，然后對信號S進行N層小波分解。找到合適的小波基對于信號的消噪是很重要的。

2)小波分解高頻系數的閾值量化，其關鍵指出就是如何選取閾值和如何進行閾值的量化，這關系到消噪的質量。

3)由小波系數進行信號重構。信號消噪的算法流程圖如圖2所示。

3.3 小波分析的信號去噪的仿真實現

利用小波分析進行信號消噪具有重要意義，它是一種時頻聯合分析方法，它在時域和頻域都具有良好的局部化特性，在信號去噪中小波變換得到了廣泛的應用。小波包分析是比小波分析更為精細的多尺度分析，小波包分析的出現也給信號去噪方法帶來了新的活力，利用小波包分析給信號去噪成為信號處理領域中的研究熱點。

3.3.1 一維平穩信號的去噪仿真

小波對平穩信號去噪處理的方法一般有三種[2,4-11]，分別為：

默認閾值消噪處理：即先在MATLAB產生信號的默認閾值，然后確定參數進行消噪處理；強制消噪處理：它是把小波分解中的高頻部分全部濾除掉，然后再對信號進行重構處理；給定軟(或硬)閾值消噪處理：閾值的取值是去噪的關鍵部分，該方式可以通過一些經驗閾值計算公式獲得閾值，這樣的值比默認的閾值更具有可信度，多次嘗試以獲得最佳消噪效果。通過含噪一維平穩信號在MATLAB中的仿真說明去噪效果 (程序略)，如圖3所示。

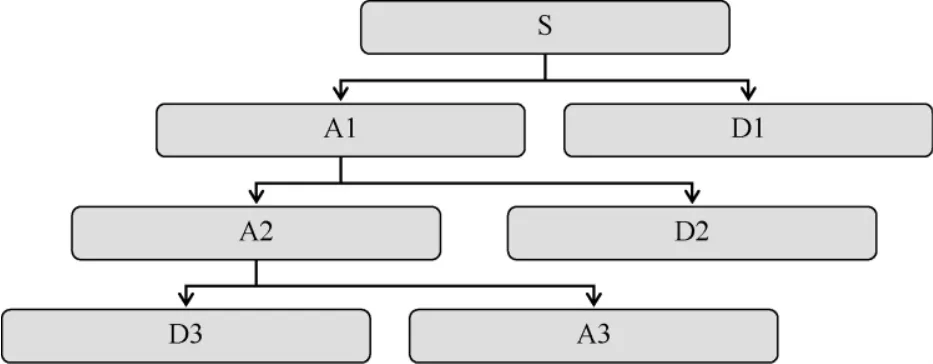
圖1 小波分解樹Fig.1 Wavelet decomposition tree

圖2 信號消噪算法流程圖Fig.2 Flow chart o f signal de-noising

從圖3可以看出，通過Fourier變換對平穩信號消噪有一定效果，但不夠理想；若采用強制消噪的方法，處理后的信號比較光滑，但同時也去掉了含噪信號中某些有用的信息；而默認閾值處理和給定閾值消噪處理則在實際應用中更實用能達到較為理想的效果。

3.3.2 一維非平穩信號的去噪

在實際工程中，我們所遇到的大部分是非平穩信號，所要分析的信號可能包含許多尖峰或突變部分，且噪聲不是平穩的白噪聲，對這種信號進行分析處理，首先要做預處理，將噪聲去除，提取有用信號。小波分析能有效區別信號中的突變部分和噪聲，從而實現非平穩信號的消噪。下面對一個含有噪聲的矩形波信號進行消噪，通過MATLAB進行仿真試驗（程序略），得到如表1和圖4所示結果。

圖3 平穩信號的去噪仿真圖Fig.3 De-noising simulation figures of stable signal

表1 對比消噪效果Tab.1 Effect of de-noising comparison

從圖4可以看出小波閾值去噪方法是最易實現、計算量最小的一種方法，但閾值的選取比較困難，另外閾值降噪對信噪比較低的信號去噪效果不是很好，本文的方案仍然需要進一步的研究和改進。用小波進行信號消噪可以很好的保持信號的尖峰和突變部分，對非平穩信號的噪聲消除具有無可比擬的優點，尤其是在確定最佳閾值后能取得很好的消噪效果.

3.3.3 基于復小波的圖像去噪

在圖像去噪方面，試驗發現復小波具有良好的去噪效果。Matlab試驗結果如圖5所示。

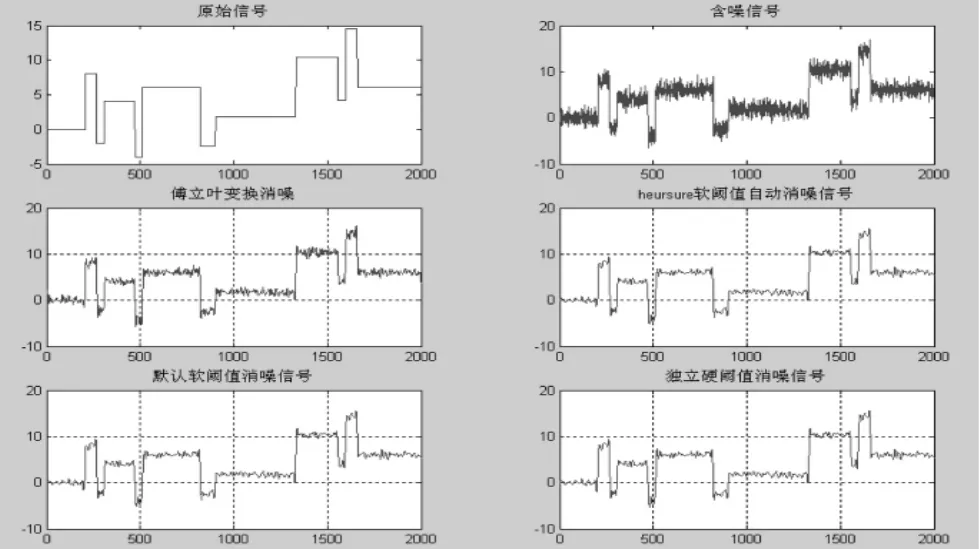
圖4 非平穩信號的去噪仿真圖Fig.4 De-noising simulation figures of stationary signal

圖5 海洋學院文心湖照片去噪Fig.5 Figure de-noising of Wenxin Lake in Zhejing Ocean University

從理論分析及仿真實驗中，都證實了當信號中含有部分較高頻信息的去噪以及減少有用高頻信號丟失方面，小波分析的效果較好。我們還可以進一步考慮選取更優的小波基或者構造新的小波基進行信號去噪，以及如何選取閾值和如何進行閾值量化。

[1]高 萍,祖 靜.基于MATLAB的小波去噪技術淺析[J].科技信息,2007(6):1-3.

[2]胡昌華,張軍波.基于MATLAB的系統分析與設計[M].西安:西安電子科技大學出版社,2000:1-6.

[3]陳 峰,成新民.基于小波變換的信號去噪技術及實現[J].現代電子技術,2005(3):11-13.

[4]劉衛國.MATLAB程序設計教程[M].北京:中國水利出版社,2005.

[5]李 瑩,孫汪典.基于MATLAB的實驗信號處理[J].暨南大學學報:自然科學版,2001,22(1):2-10.

[6]王玉平,蔡元龍.基于小波變換的濾波方法[J].信息與控制,1996,25:199-205.

[7]陳 峰,成新民.基于小波變換的信號去噪的技術與實現[J].現代電子技術,2005(3):11-13.

[8]張萬萍,陳廷槐.小波分析在一些有前景的應用領域[J].重慶大學學報:自然科學版,1999,22(1):121-125.

[9]李建平,唐遠炎.小波分析方法的應用[M].重慶:重慶大學出版社,1999.

[10]王書林.小波變換在信號去噪中的應用[J].彈箭與制導,2006,26(4):294-297.

[11]蔣東方,陳 明.一種實時小波降噪算法[J].儀器儀表學報,2004,25(6):781-783.