墜罐事故發生概率分析體系

羅華山，郭忠林

(昆明理工大學，昆明 650093)

引言

安全是人類生存和發展的基本前提，但是隨著人類的進步，工業化的發展給人們帶來巨大利益的同時也帶來了更多的危險有害因素。危險有害因素是客觀存在的，不論采取怎樣的措施都無法完全消除。但是我們可以通過系統工程的方法找出危險的存在，在一定程度上消除或減少危險有害因素。對于不能消除或減少的危險有害因素，我們也可采取相應的措施降低危險有害因素發生的概率。目前我國對事故發生概率的研究主要集中在單個元件的研究中，對于特定系統發生事故概率的研究相對較少。對于事故發生概率問題的研究主要集中在安全評價和風險評估中。而目前國內的安全評價報告和風險評估報告中又因為沒有合適的方法描述事故發生概率，因此大多都避而不談。

1 墜罐事故概率分析體系的構成

目前，對于事故發生概率的研究方法主要有：1) 對過去發生的同類事故進行大量的統計，用統計的概率進行評估；2) 事故樹的相關理論和方法。

對于過去的統計數據，統計的方法只是反映了事故的發生遵循某一概率分布，但是對于特定的礦山，如果完全依據統計出來的規律來進行概率分析，那么就會得出所有的提升系統發生事故的概率都是同等的概率。因此概率統計的方法可以揭示事故發生的概率，不能完全指出特定提升系統發生故障的概率。而基于事故樹的計算方法，難于確定基本事件發生的概率。對于特定的系統來說，沒有足夠的事故數據來確定基本事故發生的概率。但事故樹的方法給我們提供了一套很好的系統觀念和計算方法。

統計的方法可以對事故樹法中無法確定基本事件概率的問題進行很好的補充，因此可以將這兩種方法結合起來，形成一個基于統計的墜罐事故樹概率分析的方法。但是這樣還有一個統計方法的缺陷沒有解決，那就是對于統計的數據只是符合一般情況，而要應用于某一特定的系統進行分析的時候，就不能體現出系統的實際情況和統計數據之間的差異。對于偏差的問題，數學中的修正系數可以很好地解決這一問題。在結合了統計數據，事故樹和修正系數的方法的基礎上，我們可以構建如下的墜罐事故概率分析體系結構，如圖1。

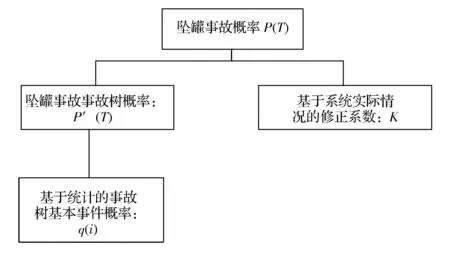
圖1 墜罐事故概率分析體系

墜罐事故發生的概率可以簡單的表達為:

P(T)=P'(T)×K

(1)

2 墜罐事故的建立和分析

事故樹的建立一般分為兩種方法：一種是計算機輔助自動建立，另一種是人工建立事故樹。對于小系統而言，一般通過人工建立事故樹的方法，采用演繹法從頂上事件開始，由上至下、循序漸進的進行。下面以提升豎井的墜罐事故為例建立事故樹[1]。

通過對近幾年提升系統墜罐事故的統計資料以及已有的分析資料的查詢，以及現場實際調查，經過分析和研究，將墜罐事故作為頂上事件T。墜罐事故的發生主要是由于鋼絲繩的斷裂和防墜器的失效等。而引起鋼絲繩斷裂的因素主要包括：超載、過速、制動裝置失靈、鋼絲繩磨損等8個。根據以上建立墜罐事故的事故樹，如圖2。

圖2 墜罐事故的事故樹

設P′(T)為頂上事件的概率，qi為基本事件的概率。事故樹的關系表達式為：

T=X9×(X1+X2+X3+X4+X5+X6+X7+X8)

(2)

故事樹最小割集有8個，根據布爾代數計算得到：

{X1,X9},{X2,X9},{X3,X9},{X4,X9},{X5,X9},{X6,X9},{X7,X9},{X8,X9}。

3 基于統計的事故樹基本事件概率

底事件發生的概率，目前主要的方法是根據經驗假設其服從指數分布[2]：

P(Xi)=1-e-λt

(3)

Xi—底事件；λ—底事件的失效率；t—系統運行時間。

λ可以根據頂上事件墜罐事故年故障次數和底事件的故障次數之比獲得。例如：X4為“緊急制動”事件，假設根據統計，1000例墜罐事故中由于緊急制動引起的事故有32起。則λ=32/1000=0.032，取t=1年。則P(X4)=1-e-0.032=0.0314934179。

根據1000起墜罐事故(包括未遂事故600起)統計資料，各基本事件所占的比例為：

同理，根據有關事故統計資料結合公式(3)得到：

P(Xi)i=1～9=0.0449580378；0.0363238647；0.0039920107；0.0314934179；0.0353597065；0.0246900880；0.0996754774；0.0353597065；0.0906270655。

根據以上分析出的事故樹最小割集和基本事件的統計學概率，可以計算出：

表1 墜罐事故統計數據

4 修正系數K的確定

事故的發生主要與人的不安全行為、物的不安全狀態以及環境的因素有關。根據美國有關方面的統計，某年全國休工8 d以上的事故中，有96%的事故與人的不安全行為有關，91%的事故與物的不安全狀態有關。日本全國某年休工4 d以上的事故中，有94.5%的事故與人的不安全行為有關，83.5%的事故與物的不安全狀態有關[2]。

由以上數據可知，事故發生的兩個主要因素是人的不安全行為和物的不安全狀態。由于環境的因素在事故中所占的比例比較小，故在此忽略。從而設：

K=αK1+βK2

(4)

α：人的不安全行為權重系數；β：物的不安全狀態權重系數；K1：人的不安全行為修正系數；K2：物的不安全狀態修正系數。

根據美國和日本對人的不安全行為和物的不安全狀態的統計研究，設以上事故中人的不安全因素所占比例為ai，物的不安全狀態所占的比例為bi，則在忽略環境因素的境況下，可得到α、β為：

由此得到:K=0.52K1+0.48K2

(5)

由于事故發生的概率P＇(T)，P(T)∈[0,1]，

對于人的不安全行為和物體的不安全狀態，單獨考慮人的不安全行為時，修正系數：K=K1。設人的安全行為狀態值為L1，存在函數映射f1，則：K=f1(L1)。

(6)

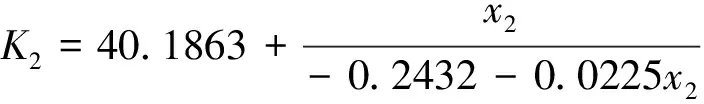
(7)

x1—人的安全行為評分值；x2—物的安全行為評分值。

其曲線圖如圖3、圖4所示：

圖3 K1與人的安全行為評分值x 1之間的關系圖

圖4 K2與人的安全行為評分值x2之間的關系圖

從圖中可以看出：當人的不安全行為較少，即人的行為安全程度較高時，隨著分值的提高，K值變化程度較小；而當人的不安全行為較多，即人的行為安全程度較低的時候，分值的變化會引起K1的較大波動。而這一現象與實際中人的不安全行為和事故發生的關系相一致。而物的不安全狀態之間也遵循同樣的規律。因此說明了，該插值分析的結果具有較好的指導意義。只要對系統中存在的人的不安全行為和物體的不安全狀態進行評分，轉化成百分數并代入公式(6)、(7)中，即可得出兩個系數修正值。

5 結論

本文結合了統計學、事故樹以及數學修正的方法，提出一套墜罐事故發生概率的計算方法。該方法使得事故發生概率的計算成為可能，修正系數結合了系統的實際情況，使得計算出的數值更接近于真實情況。本論文只是從方法上提出了可行性和可操作性，而在實際應用當中還應該對事故樹的建立，參數的選取進行更深入的探討。作為多種方法綜合合成的方法體系，對相關領域的研究和實踐提供了有意義的指導作用。

[1] 魯青，徐文尚，劉志海，等. 基于FTA的礦井提升鋼絲繩斷繩故障分析[J]. 煤礦機械，2006(2):356.

[2] 徐志勝. 安全系統工程[M]. 北京：機械工業出版社,2007.

[3] 吳瓊. 安全管理學[M]. 北京：煤炭工業出版社,2002.

[4] 李慶揚,王能超,易大義. 數值分析[M]. 北京: 清華大學出版社，2001.

[5] Walter Gander. 用Maple和Mat lab解決科學計算問題[M]. 高等教育出版社，1999.

[6] 張韻華,王新茂. 符號計算系統Maple教程[M]. 中國科學技術大學出版社，2007.