南芬露天礦攔水壩滲流與應力耦合分析

李有臣，董憲偉，蔡嗣經

(1．北京科技大學 土木與環境工程學院，北京 100083；2. 本溪鋼鐵(集團)有限責任公司， 遼寧 本溪 117000)

引言

攔水壩壩址區的地形條件、水文地質條件一般較為復雜，主要表現為覆蓋層較厚且分層較多。為了提高壩體的安全性和穩定性，在攔水壩建設之前，首先要對整個壩區的水滲流情況有較全面地了解。根據壩區的工程地質和水文資料，將各地層的滲透特性進行有效地模擬，分析壩體內部滲流場、應力場的相互影響和相互作用，為改善壩體弱應力區和選擇心墻提供依據。

1 攔水壩及壩區水文、工程地質概況

本鋼南芬攔水壩為土石壩，壩高32 m，頂寬6 m，邊坡比1︰2，最高洪水位28 m，壩體內擬設心墻或其它防滲措施。壩址區為山間U型河谷，原有一小溪流通過，小溪枯水期流量為10 m3/s，洪水期大于500 m3/s。兩側山體坡度20°～ 30°，植被發育。兩側山體為花崗巖，風化層厚度小于5 m。右壩肩為塊石混雜砂壤土：松散，塊石堅固，一般粒徑200～500 mm，最大1 500 mm，無磨圓，無分選；河谷區為漂石-卵石混雜砂礫土：松散，塊石堅固有磨圓，無分選，一般粒徑200～50 mm，最大1 500 mm，厚度約15 m；左壩肩為塊石充填黃色粘土，無架空現象，塊石成分、組分同右壩肩。兩側壩肩在勘探深度內(孔深最大15 m)未見穩定地下水水位[1]。攔水壩縱剖面如圖1所示。

圖1 攔水壩心墻示意圖

土石壩壩體內部的受力是由內部的滲流場和應力場相互影響、相互作用的結果。一方面，滲流場的改變引起滲流體積力和滲透壓力的改變，使壩體作用的外荷載發生變化，從而改變了壩體應力場的分布；另一方面，應力場的改變引起體積應變的改變，使壩體各部位的孔隙率發生變化，滲透系數隨之變化，從而也改變了壩體滲流場的分布。滲流場與應力場相互作用、相互影響會使雙場耦合達到某一平衡狀態，分別形成滲流場影響下的穩定應力場與應力場影響下的穩定滲流場[2-4]。目前對流固耦合問題的研究主要基于有限元方法。并且大多集中在裂隙巖體滲流場與應力場的耦合分析上，實際水利工程中，碾壓混凝土壩、土石壩等壩體滲流與應力也存在著較強的耦合作用[5-8]。

2 工程分析

2.1 加載及邊界條件

1)土壩中設計心墻的滲透系數遠遠低于周圍土體的滲透系數，認為是不透水材料；

2)水載荷作為靜止載荷適用于攔水壩體，最高水位為28 m；

3)計算時重點考慮最高水位的載荷；

4)壩體底部側邊界為零流量邊界，且在計算過程中水位邊界條件不變。

2.2 計算模型

采用工程分析軟件FLAC3D建立分析模型，以壩體平行軸線方向為Y軸，垂直地表方向為Z軸，水平方向為X軸，建立三維有限差分析模型，如圖2所示。

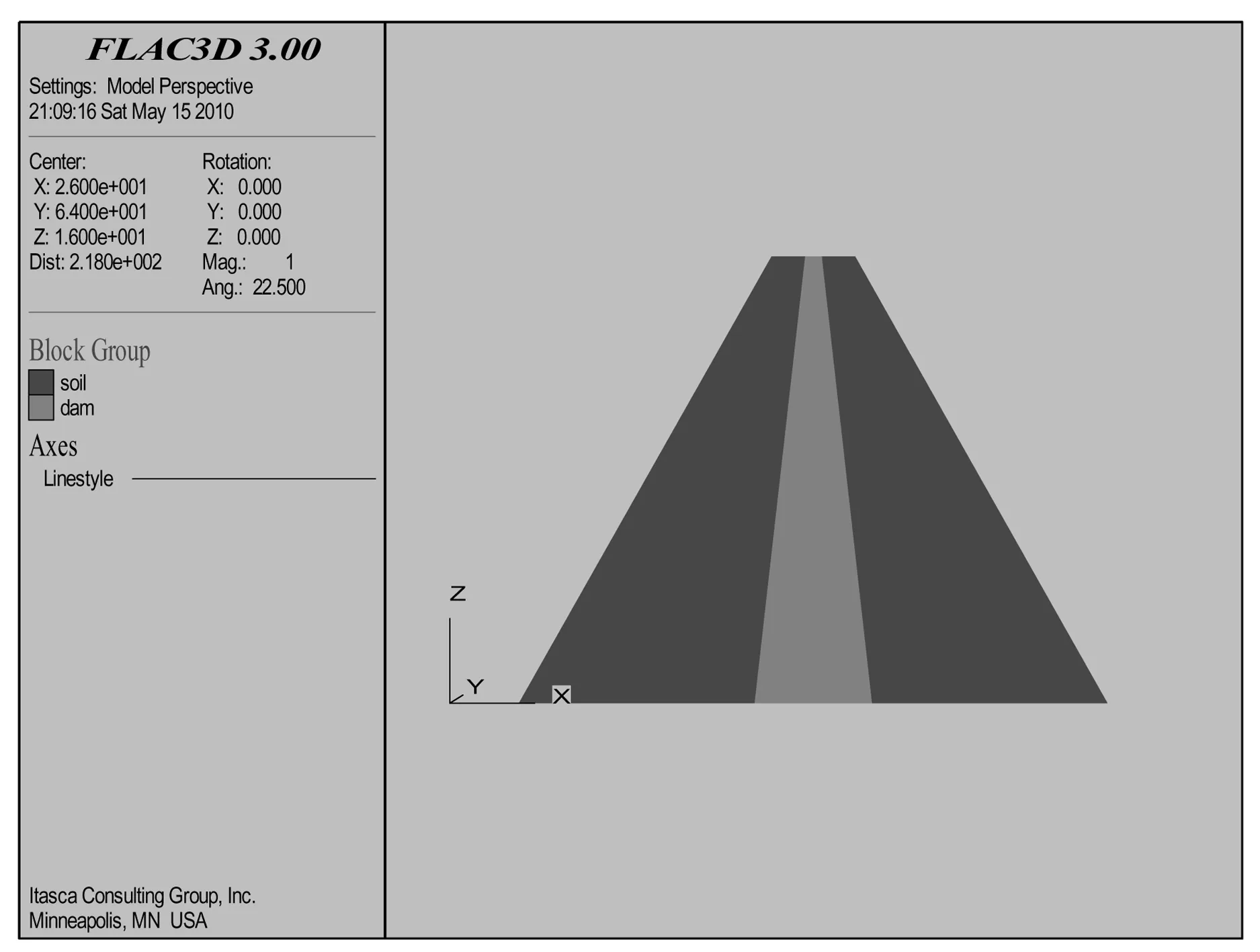
圖2 攔水壩心墻三維模型

在計算過程中，根據該工程的地質勘察報告、水文資料，計算力學參數取值如下：體積模量為30 MPa，剪切模量為10 MPa，重力方向為垂直向下，大小為10 m/s2，流體的密度為1 000 kg/m3，滲透系數(各向同性滲透模型)為10-10m2/Pa-sec，孔隙率默認為0.5，流體抗拉強度為-1010MPa。

2.3 計算結果分析

1)壩體應力分析。

圖3～圖6分別是壩體水位上升前后的大小主應力等值線圖。水位高度的變化引起壩體大小主應力的分布情況發生了改變。應力分布主要特點是：起初應力分布沿壩軸線近似成對稱分布，但是隨著水位的變化，在壩體內部防滲心墻的作用下，壩體應力將進行二次調整；防滲心墻內部的大小主應力基本不變，而防滲墻附近，即防滲墻帶和壩體連接處大小主應力變化較大，最大值達521 kPa。應力變化的原因是由于水位上升導致壩體砂石料產生濕陷固結的結果。

圖3 初始最大主應力云圖

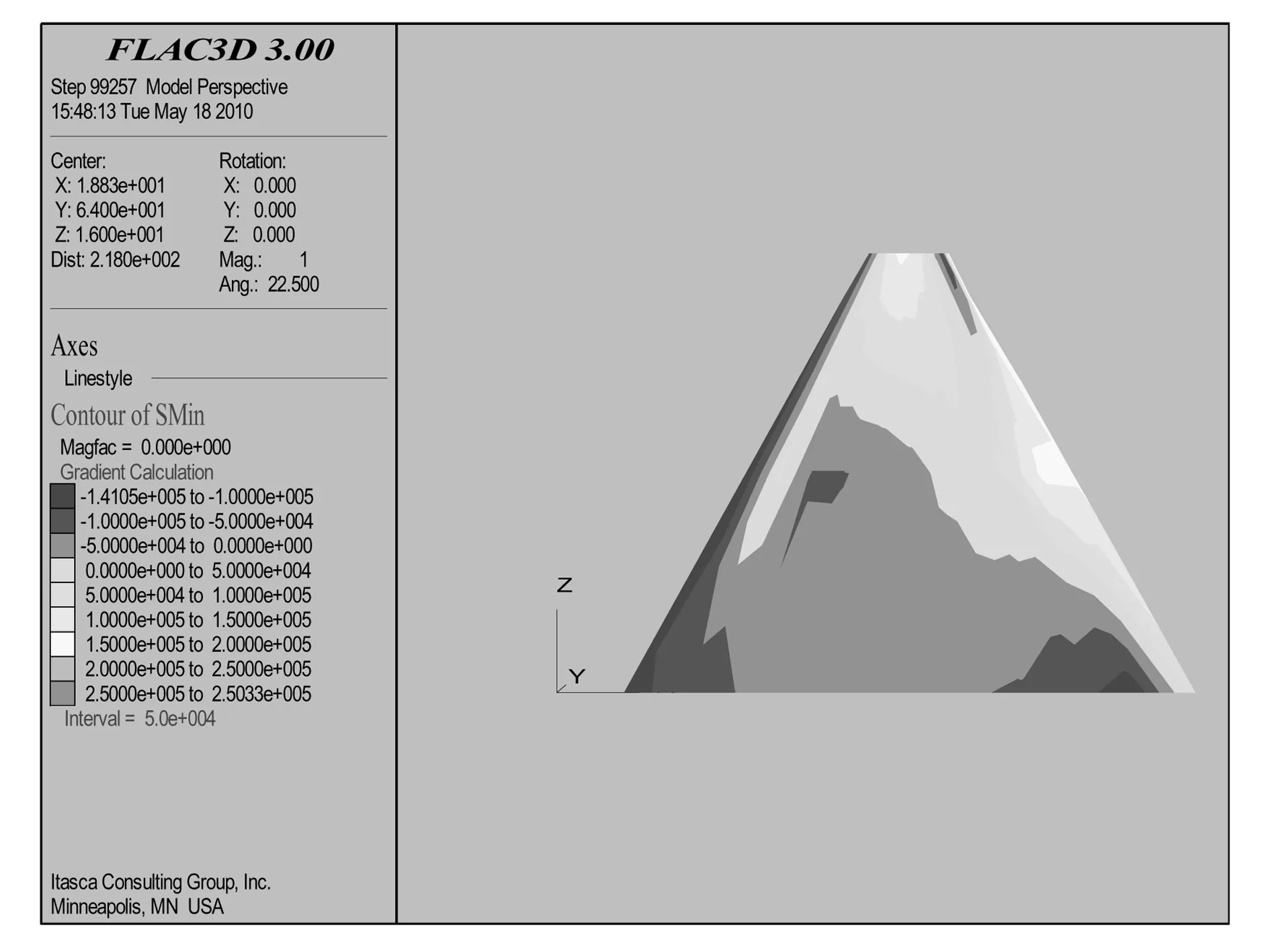
圖4 初始最小主應力云圖

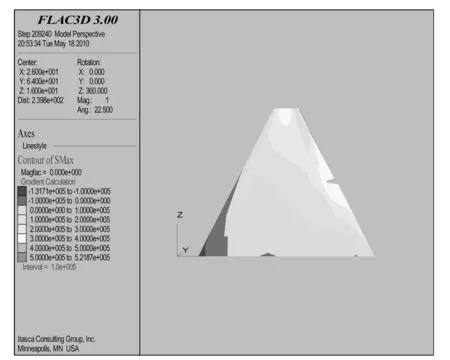
圖5 最高水位的最大主應力云圖

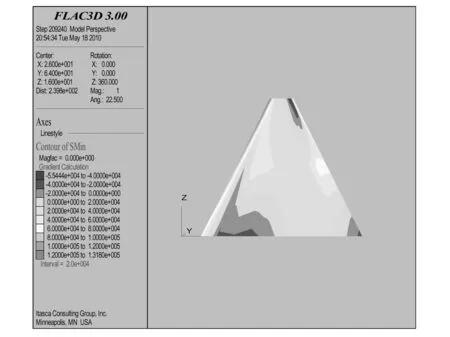
圖6 最高水位的最小主應力云圖

2)壩體位移云圖分析。

圖7～圖10分別為初始應力、最高水位壩體垂直和水平位移等值線云圖。圖7和圖9分別表示初始應力和最高水位的壩體垂直位移等值線云圖；圖8和圖10分別表示初始應力和最高水位的壩體水平位移等值線云圖。經過分析可以看到，最大豎向位移和最大橫向位移均有所減小，有利于壩體的穩定。

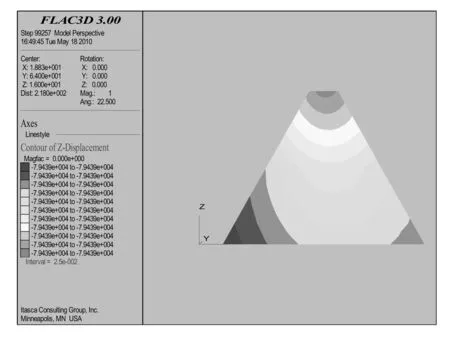
圖7 初始應力的z向位移云圖

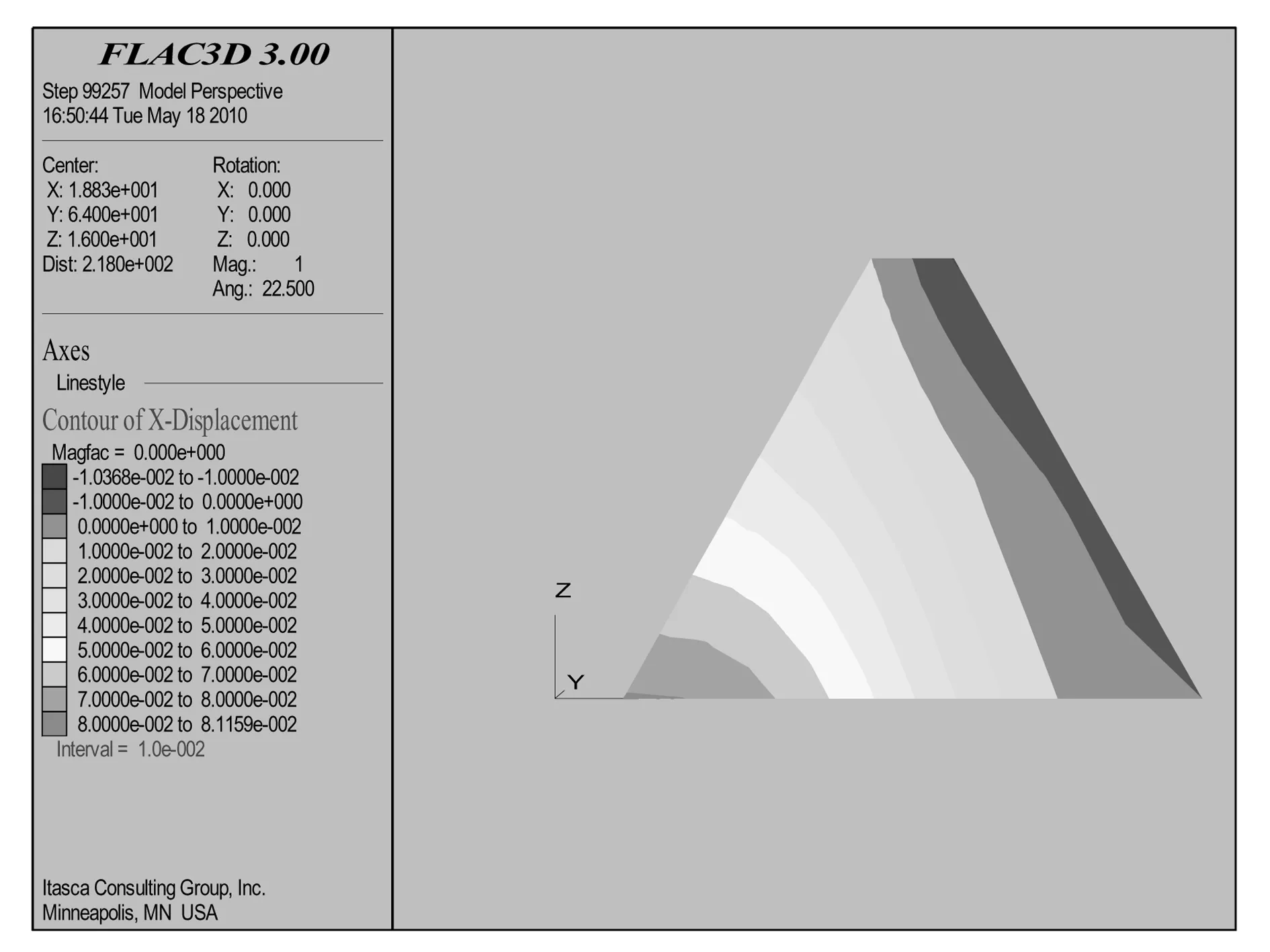
圖8 初始應力的x向位移云圖

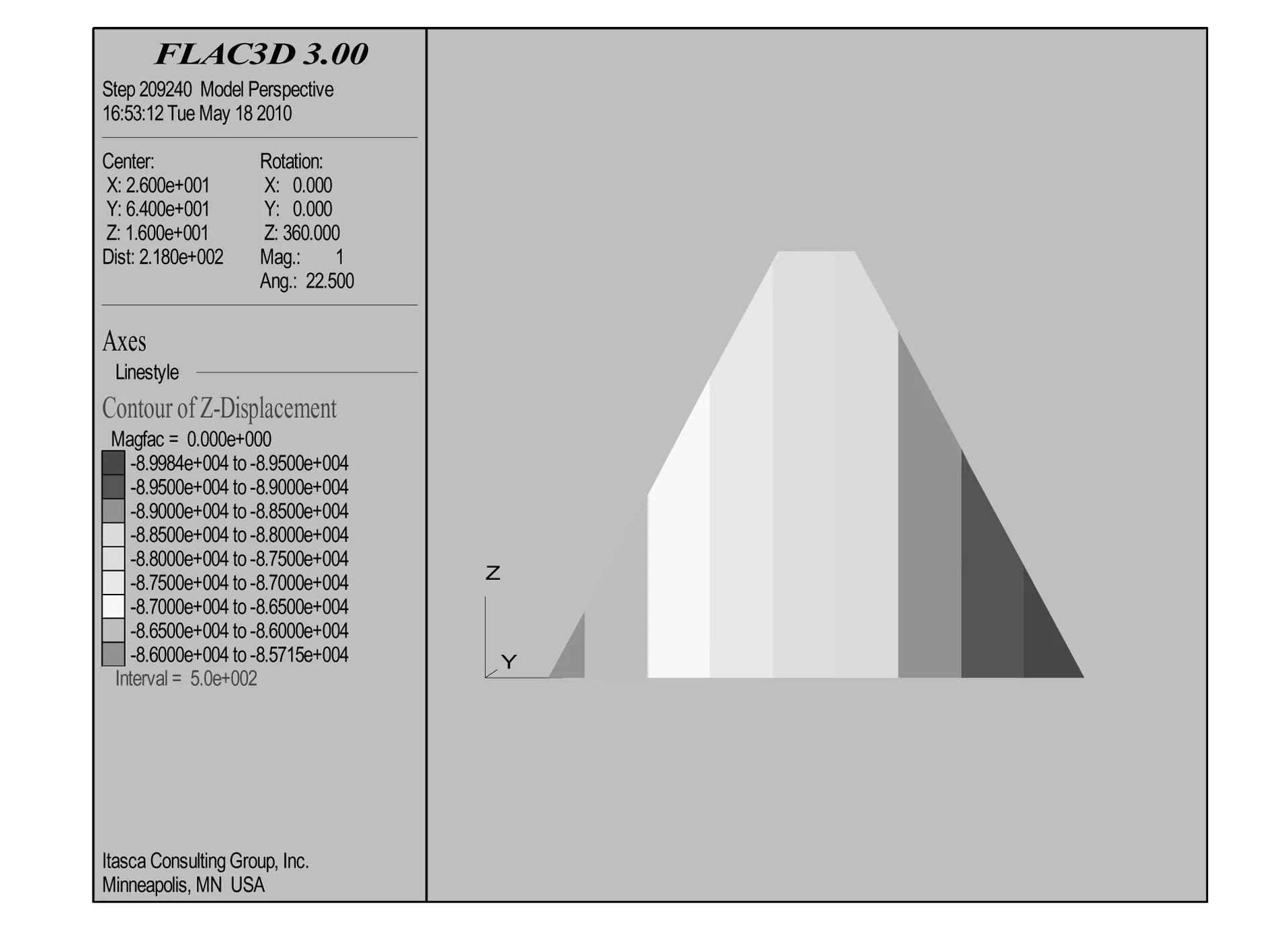
圖9 最高水位的z向位移云圖

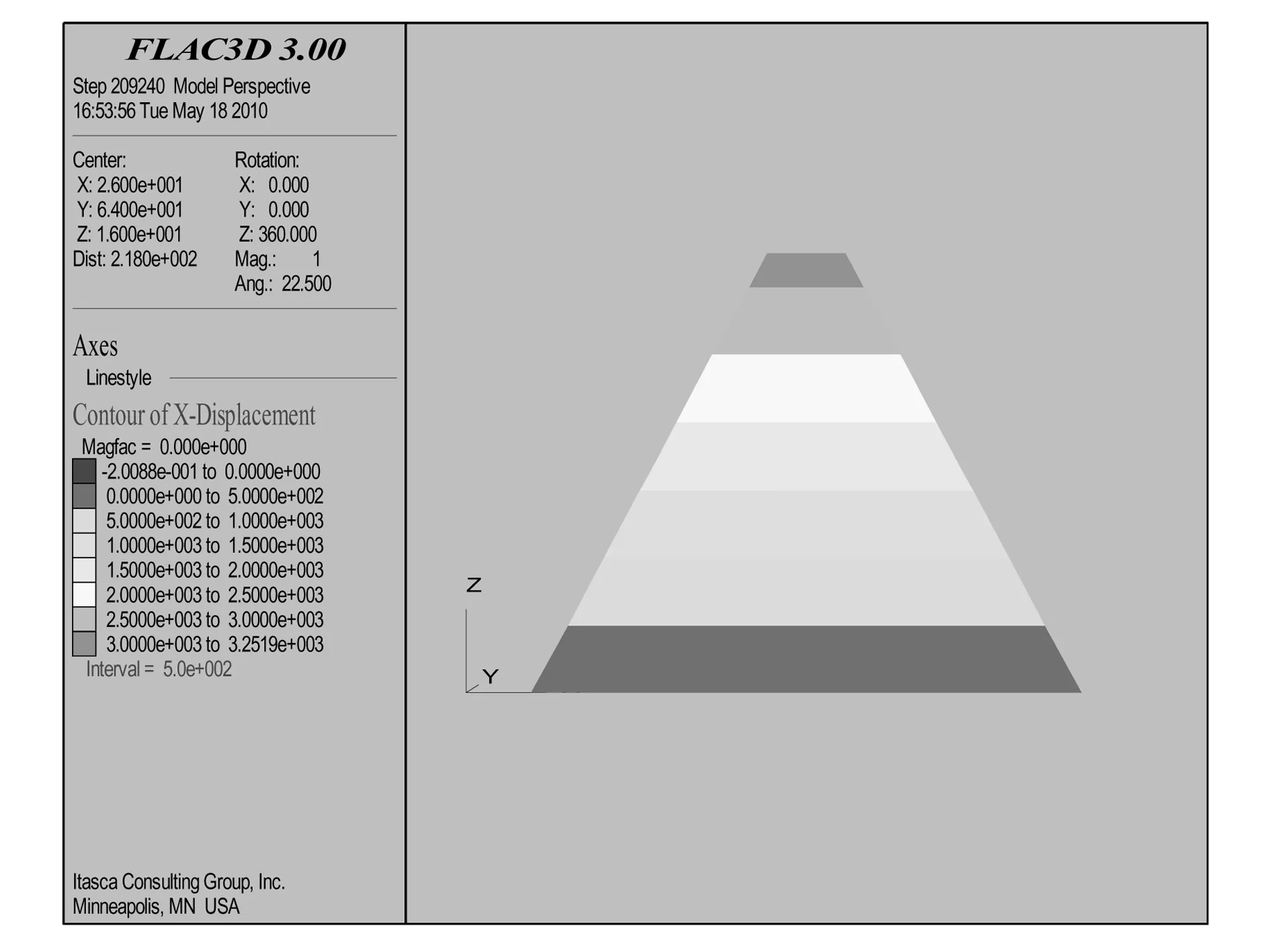
圖10 最高水位的x向位移云圖

3)壩體滲透孔隙水壓力分析

圖11、12分別為初始應力的孔壓云圖和最高水位壩體的滲透孔隙水壓力云圖。比較分析可知，在攔水壩體設置防滲心墻，可有效改善壩體的孔隙水壓力分布，達到壩體防滲加固的要求。

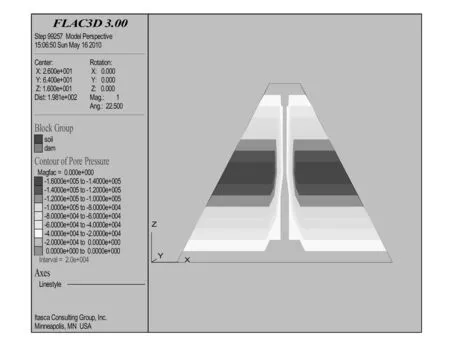
圖11 初始應力的孔壓云圖

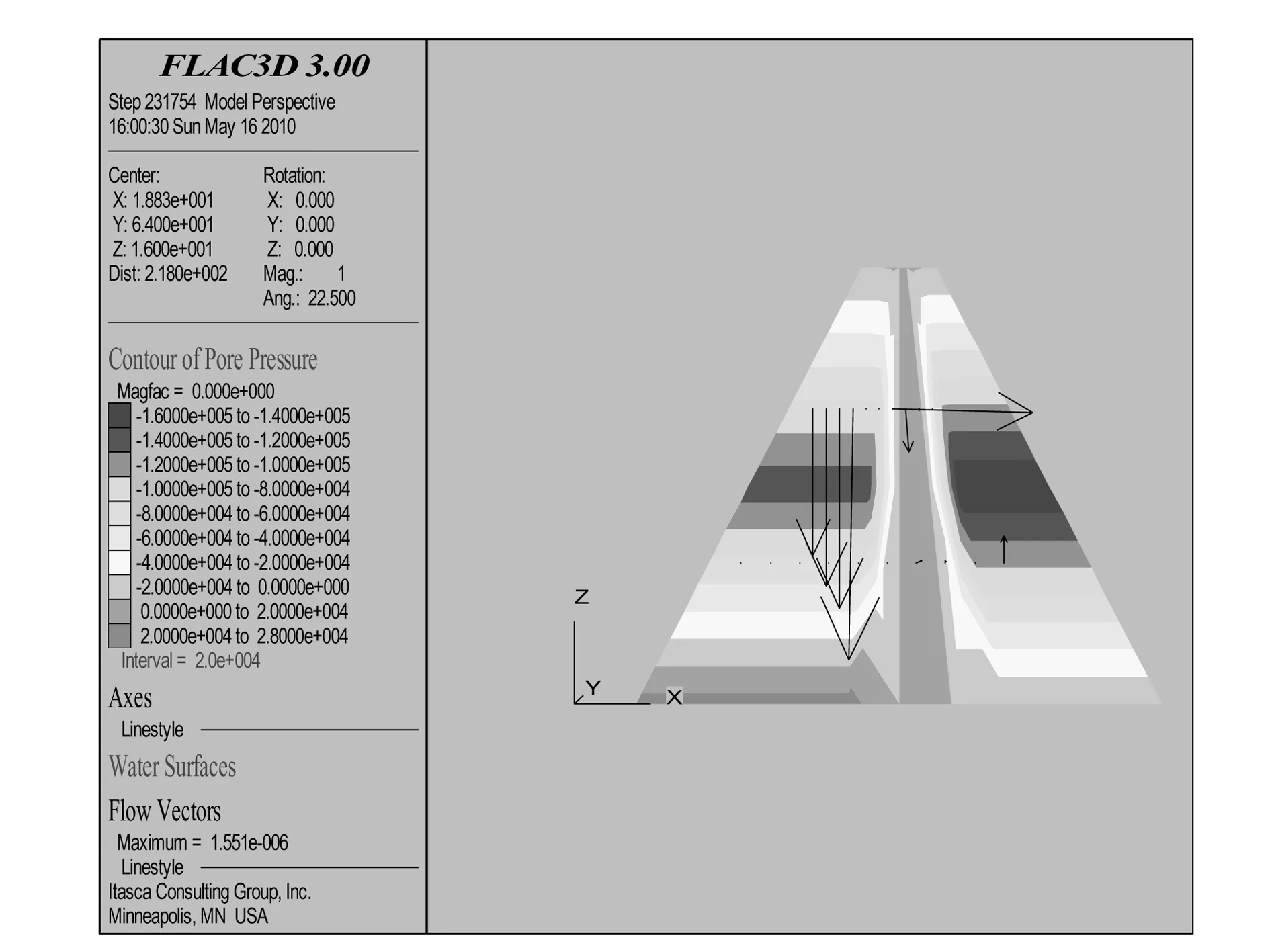
圖12 最高水位的孔隙水壓力云圖

3 結論

1)心墻壩體在水載荷為零時，壩體的最大主應力和最小主應力近似對稱地分布在心墻兩側。水位上升到最高點時，壩體主應力的最大值出現在左側壩基處，應力水平等值線圖顯示了整個壩體處于安全穩定狀態[9]。

2)應用FLAC3D軟件對心墻土壩滲流過程進行分析，可以補充壩體弱應力區，調整大小主應力，改善壩體的穩定性。

3)三維快速拉格朗日分析方法可以較好地模擬土體材料的彈塑性力學模型[10]，與其它數值方法相比，該方法較簡單，考慮影響因素少，并且計算結果與實際情況較接近。

[1] 張洪斌,孫永平,李萬福,等. 本鋼南芬攔水壩壩基滲透變形勘察[J]. 黑龍江水專學報, 2004, 31(1)：12.

[2] 項顏勇. 裂隙巖體中非飽和滲流與運移的概念模型及數值模擬[J]. 工程地質學報,2002,10(2)：204-209.

[3] 張國,朱濟祥,莊軍,等．巖質邊坡穩定性的滲流耦合分析[J]. 天津大學學報,1999,32(5)： 560-564.

[4] 陳平, 張有天．裂隙巖體滲流與應力耦合分析[J]. 巖石力學與工程學報, 1994, 13(4)： 299-308．

[5] Oda M．An equivalent continuum model far coupled stress and fluid flow analysis in jointed rock masses[J]. Water Resources Research,1986(13)：1854-1865.

[6] 柴軍瑞,仵彥卿．均質土壩滲流場與應力場耦合分析的數學模型[J]. 陜西水力發電, 1997, 13(3)：4-7.

[7] S Christensen, K R Rasmussen, K Moller. Prediction of regional groundwater flow to streams[J]. Groundwater, 1998, 36(2)：53-66.

[8] 陳曉平,茜平一,梁志松．非均質土壩穩定性的滲流場和應力場耦合分析[J]. 巖土力學，2004, 25(6)：860-864.

[9] 王祖強,張貴金,王明. 用FLAC3D模擬流固耦合評價病險土壩防滲加固效果[J]. 湖南水利水電, 2009(2)：41-43.

[10] 葛暢,張允亭. 本鋼南芬攔水壩壩基滲透變形勘察-關于碎石類土的滲透變形試驗[J]. 油氣田地面工程, 2003(12)：37.