液流儲能電池模擬研究的進展

邢 楓,張華民,馬相坤,王曉麗

(1.中國科學院大連化學物理研究所,遼寧大連 116023；2.大連融科儲能技術發展有限公司,遼寧大連 116025)

近年來,大部分研究者致力于液流儲能電池關鍵材料的研究,如電解液、離子交換膜、雙極板和電極等,但液流儲能電池是一個結構復雜、包含多個過程的耦合系統,電池結構、電池內部反應、傳遞過程及電流密度分布等對液流儲能電池的性能都起著重要作用[1]。

模擬仿真技術已成為研發的一個重要手段。通過建模分析液流儲能電池內部傳遞反應過程,獲得實驗無法測量的重要參數,可調整設計方案、優化參數、預測各種工況條件下的電池性能,為結構設計和性能優化提供理論指導。

按照模型的復雜程度,液流儲能電池數學模型可分為零維、一維及二維模型。本文作者介紹了液流儲能電池模擬研究的現狀,重點闡述了上述模型及漏電電流模型的特點、研究進展及局限性,綜述了液流儲能電池模擬常用的商業化軟件,并對液流儲能電池模擬的發展方向進行了展望。

1 數學模型

1.1 零維模型

零維模型適用于對系統動態時域與頻域響應的研究。K.Enomoto等[2]基于電路響應原理,建立了儲能用全釩液流電池(VRB)的等效電路模型,利用電路暫態響應原理,剖析VRB暫態行為與電化學反應的關系,研究了等效電阻與電解液荷電狀態(SOC)的關系。M.H.Li等[3]建立了動態模型,研究濃度對儲能用VRB暫態行為的影響。該模型將化學反應速率與外電路電流聯系起來,耦合濃度方程和能斯特方程,并認為釩離子濃度的改變是影響電池系統動態特性的主要因素,優化電解液流量可提高輸出電壓和延長放電時間,電池系統的頻率響應取決于電池與電解液儲罐的體積比。A.A.Shah等[4]建立了用于控制和監控的單元電池尺度的動態模型。該模型基于守恒定律,考慮主要電阻、電化學方程和循環系統特征,以便快速求解,滿足控制要求。

零維模型的優點明顯,方程簡單易解,適合于電池系統控制的開發和設計,但不能進行電池內部機理的深入研究。

1.2 一維模型

J.W.van Zee等[5]建立了適合于評價鋅溴液流儲能電池系統性能的一維模型。在給定的幾何尺寸和物理特性參數條件下,推導出以系統效率為目標函數,綜合泵功耗和漏電損耗,以電解液內阻和流道寬度為因變量的復雜函數。該模型可進行參數優化,降低電池系統的能量損失,但未考慮電化學反應及電解液內阻隨溫度變化的影響。D.P.Scamman等[6-7]結合輸運方程和Butler-Volmer方程,建立了溴-多硫化物電池的一維模型,可預測組分濃度等參數沿電極方向的變化,獲得電池系統能量效率及功率密度等參數,將參數優化和成本、利潤等商業化過程結合后,可用于大型實際項目。A.A.Shah等[8]建立了二維 VRB模型,M.Vynnycky[9]將量綱化和漸進分析法用于該模型,簡化為具有一維瞬態擴散方程特征的方程組,降低了電池放大后模型對計算機硬件的要求,可快速獲得操作條件變化的電池模塊響應信息。

一維模型與零維模型特點相似,能一定程度上預測電池的性能,適合于電池模塊和電池系統規模放大效應的研究。

1.3 二維模型

P.S.Fedkiw等[10]建立了鐵鉻單電池二維等溫模型,運用基本守恒方程及Butler-Volmer方程,考慮鉻電極側的析氫反應,分析了電極尺寸、電解液流動方式、運行溫度等的影響,發現電極厚度、電池電壓及電解液流量的優化,可提高庫侖效率,提高運行溫度,可提高能量效率,縮短充電時間。

基于二維模擬理論,結合對流擴散方程和Butler-Volmer方程,形成了多種描述鋅溴電池的數學模型,如薄擴散層模型及文獻[11]中的模型,旨在探索影響鋅溴電池能量效率的關鍵因素及相互作用,控制鋅電極枝晶的產生,避免流道堵塞、甚至電池短路。薄擴散層模型只在反應物轉化率很低、充放電電流不大時成立,并認為流道內大部分區域的反應物濃度是常數,僅在靠近電極的薄層內,才會發生化學反應。R.A.Putt[12]利用該模型優化設計參數:通過減小鋅溴濃度、增加流道寬度和電極厚度、減小電極動力學參數及質量擴散系數等方法,提高負極板上電流密度分布的均勻性,但簡化了溴多孔電極特性對傳質和電化學反應的影響。J.Lee等[13-14]在文獻[12]中模型的基礎上,用無量綱參數法進一步考慮隔膜及終端電阻對電池性能的影響,發現:在給定平均電流密度時,終端電阻對電流密度的均勻化存在最優值,在忽略電池電勢的情況下,隔膜內阻越高,電流密度分布均勻性越好。該模型還可預測鋅電極的腐蝕率,確定控制腐蝕率的關鍵無量綱參數；在此基礎上加入時間項,可獲得電極上電流密度分布隨時間的變化,并將描述電池行為的宏觀模型與描述鋅枝晶現象的微觀模型結合起來,模擬枝晶的生長情況及對流道結構和濃度分布的影響。模擬發現:在高充電電壓下,平均電池電流快速下降；在充電末期提高電解液流速,可增大平均電流密度。薄擴散層模型雖然應用廣泛,但不能計算反應物的轉化率,不能獲得電池能量效率等關鍵參數。M.J.Mader等[15]提出更合理的假設,考慮鋅電極上的溴的副反應,建立了適應性更強的二維模型,分析多個外部參數(流道寬度等)的關系及對電池性能的影響,獲得反應物的轉化率和電池能量效率,但只能模擬充電過程,并未考慮多孔溴電極的影響。模擬發現:增加隔膜厚度雖然會在充電初期降低電池的能量效率,但隨著充電的進行,能量效率反而會提高。T.I.Evans等[11]在此基礎上補充溴多孔電極模型,模擬了完整的充放電,分析了溴多孔電極厚度等參數對電池效率的影響,認為增加多孔電極厚度,有利于提高電池的能量效率,證明了鋅溴電池能量效率可達70%的可能性。

D.J.You等[16]采用無量綱化方法,結合多孔電極理論,建立了流通型多孔電極的二維半電池理論模型,發現:增強對流傳質、提高電解液電導率、減小擴散阻力等方法可使電解液濃度和電流密度分布更均勻,并降低反應層的厚度。A.A.Shah等[8]利用傳遞現象的基本理論,綜合動量守恒方程、對流擴散方程、電荷守恒方程和Butler-Volmer方程,基于計算流體力學(CFD)方法建立了VRB二維瞬態模型,研究認為:提高電解液濃度和流速有利于提高庫侖效率；減小電極孔隙率,可促進過電位和傳遞電流密度在電極中的均勻分布；孔隙率和電解液流速越小,發生副反應的概率就越大。D.J.You等[17]用電解液SOC定義電解液中反應物與生成物的濃度,將文獻[9]中的模型簡化為穩態模型,且不考慮電中性條件和離子在電場作用下的遷移。該模型闡述了電流、電解液SOC、電極孔隙率及電極表面傳質系數的變化對過電位、傳遞電流密度及電解液濃度分布規律的影響,表明:電極反應速率幾乎與充放電電流密度線性正相關；過電位在SOC=50%時最小,并在充放電末期急劇增大,引起副反應；增大表面傳質系數能減輕電極極化。

VRB在充放電過程中伴隨著熱量的產生,H.Al-Fetlawi等[18]在文獻[9]中的模型基礎上考慮非等溫效應,加入能量方程,研究電池內的溫度分布,不僅分析了電池的熱源(活化損失熱、反應熱和歐姆熱),還考慮了溫度變化對材料物理性能和電化學參數的影響,并認為:在高工作環境溫度和負載下,電池內的高溫不僅對全氟離子交換膜有很大的危害,還會增加集流板腐蝕和副反應發生的概率；調節電解液流量和充放電電流密度,能顯著改變電池內部的溫度分布和發熱量。A.A.Shah等[19-20]參考兩相流方法,研究了VRB內的析氫、析氧副反應,增加的氣泡輸運方程和氣液滑移速度描述了氣、液兩相在電極中的輸運過程。有關運行溫度、反應物濃度、電解液流量及氣泡直徑對副反應和電池性能影響的考察表明:副反應不僅減小了電化學反應的活性面積,而且消耗了充放電電流。D.J.You等[21]建立二維模型預測VRB的自放電,發現釩離子的擴散速率取決于在膜中的擴散系數、無量綱分配系數及兩側半電池中釩離子的濃度梯度。

二維模型綜合考慮動量方程、組分輸運方程、電荷守恒方程及電化學方程,研究液流儲能電池的影響因素及相互作用關系。與零維模型和一維模型相比,二維模型有助于研究物理現象的本質規律,更注重研究電池的內部運行機理。

1.4 漏電電流模型

液流儲能電池模塊由多只單體電池按壓濾機方式組裝,正、負極電解液分別由公用管路,經分支管路進入各單體電池的正、負極,帶有離子導體的電解液通過單體電池之間的分支管路和公用管路連通起來產生漏電電流,如圖1所示。同理,在液流電池系統中,電池模塊之間也存在漏電電流。

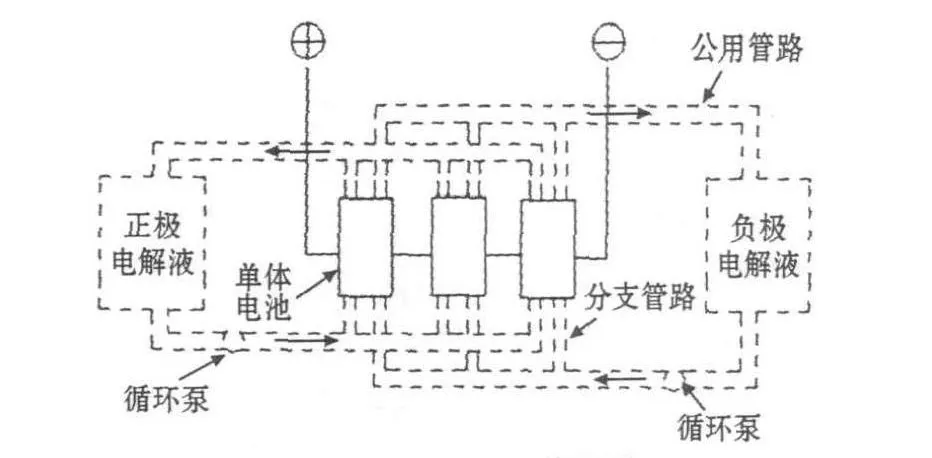
圖1 漏電電流原理圖Fig.1 Principle diagram of shunt current

漏電電流的產生不僅會削弱電池性能,降低電池效率,還會引起其他副反應(析氫、析氧和電極腐蝕等),是影響液流電池性能的關鍵因素之一。漏電電流的研究主要集中于模擬研究,模型是基于基爾霍夫定律和歐姆定律建立的等效電路模型。按電池的結構,主要分為無隔膜和有隔膜的模型,文獻[22]給出了有離子交換膜的液流儲能電池電路圖。

E.A.Kaminski等[23]針對無隔膜和有隔膜的液流儲能電池提出計算漏電電流的方法,計算了由20只單體電池組成的電池模塊在公用管路和分支管路中的漏電電流分布。R.E.White等[24-25]對具有非對稱和對稱電路結構,以及具有非線性電路元件的電池模塊建立了等效電路模型,并進一步拓展為公用管路為導體的情況。分析指出:若公用管路電解液電勢差大于水解電壓,則會出現析氫、析氧現象,因此雙極電池模塊須將與電解液接觸的非電極區絕緣化。上述模型雖然能預測漏電電流的分布情況,但忽略了在充放電過程中電池電壓變化對漏電電流的影響。尤東江[26]考慮了電池電壓和漏電電流隨時間的變化,獲得了電池組充放電電壓模擬曲線、電池組漏電電流及其分布情況,認為降低電池過電位,可減小漏電損失,并且估算了電池組的容量損失情況,對影響庫侖效率的關鍵因素進行了分析。漏電電流模型的研究,為降低、甚至消除漏電電流提供了理論依據。

2 模擬軟件

從基礎理論出發建立數學模型并研究計算方法,是非常耗時的,不利于研究者研究物理化學過程的本質,利用商業化軟件是一種有效的方法。目前,用于液流儲能電池模擬研究的商業化軟件主要是COMSOL Multiphysics,而FLUENT軟件具有極大的潛力。COMSOL Multiphysics軟件基于有限元理論開發,適合于求解多維、多物理場耦合模型。該軟件開發的電池與燃料電池模塊,結合流動模塊、質量輸運模塊和PDE模塊,廣泛用于固體氧化物燃料電池(SOFC)及質子交換膜燃料電池(PEMFC)的二維、三維單體電池和電池模塊的模擬,本文介紹的VRB二維模型均基于COMSOL Multiphysics軟件完成。該軟件雖是液流儲能電池與燃料電池模擬研究常用的工具,但在研究規模放大效應時的局限性明顯,而FLUENT軟件在這方面具有優勢。FLUENT軟件基于有限體積法開發而成,保證了方程的守恒性。FLUENT軟件推出了燃料電池模塊用于SOFC和PEMFC建模研究,雖然暫時未用于液流電池領域,但強大的用戶自定義函數(UDF)和用戶自定義標量方程(UDS)功能,在電池規模放大研究中擁有一定的優勢。

3 小結及展望

綜上所述,液流儲能電池模擬研究主要集中在零維模型、一維模型和二維模型的建模和分析,缺乏三維數學模型方面的研究。零維模型和一維模型從液流儲能電池系統的角度出發,研究電池系統的動態響應,但忽略了電池內部機理；二維模型對電池內部傳遞過程進行理論分析,但是電池結構的忽略,不能為電池設計提供充分的理論依據。液流儲能電池三維模擬是進一步研究的重點之一,研究電池結構、電極尺寸、流場、電解液流道、材料物性、漏電損耗等對液流儲能電池性能的影響,揭示流體、濃度、電流密度、過電位等在三維空間中的分布規律,為液流儲能電池模塊優化提供理論指導；液流儲能電池系統模型是研究的另一個重點,綜合泵耗、漏電損耗、熱處理功耗等建立液流儲能電池系統模型,優化液流儲能電池系統配置,提高液流儲能電池系統效率。

隨著液流儲能電池產業化的進一步推進,液流儲能電池結構、性能、穩定性、可靠性等需要進一步完善,因此對液流儲能電池內部的物理化學過程需要更深入的探索。

[1]ZHANG Hua-min(張華民),ZHANG Yu(張宇),LIU Zong-hao(劉宗浩),et al.液流儲能電池技術研究進展[J].Progress in Chemistry(化學進展),2009,21(11):2 333-2 340.

[2]Enomoto K,Sasaki T,Shigematsu T,et al.Evaluation study about redox flow battery response and its modeling[J].IEEJ T ransaction on Power and Energy,2002,122(4):554-560.

[3]Li M H,Hikihara T.A coupled dynamical model of redox flow battery based on chemical reaction,fluid flow,and electrical circuit[J].IEICE T ransaction on Fundamentals of Electronics,Communications and Computer Sciences,2008,E91-A(7):1 741-1 747.

[4]Shah A A,Tangirala R,Singh R,et al.A dynamic unit cell model for the all-vanadium flow battery[J].J Electrochem Soc,2011,158(6):A671-A677.

[5]van Zee J W,White R E,G rimes P,et al.Electrochemical Cell Design[M].New York:Plenum Publishing Co.,1984.293.

[6]Scamman D P,Reade G W,Roberts E P L.Numerical modeling of a bromide-polysulphide redox flow battery(Ⅰ).Modeling approach and validation for a pilot-scale system[J].J Power Sources,2009,189(2):1 220-1 230.

[7]Scamman D P,Reade G W,Roberts E P L.Numerical modeling ofa bromide-polysulphide redox flow battery(Ⅱ).Evaluation of a utility-scale system[J].J Power Sources,2009,189(2):1 231-1 239.

[8]Shah A A,Watt-Smith M J,Walsh F C.A dynamic performance model for redox-flow batteries involving soluble species[J].Electrochim Acta,2008,53(27):8 087-8 100.

[9]Vynnycky M.Analysis of a model for the operation of a vanadium redox battery[J].Energy,2010,36(4):2 242-2 256.

[10]Fedkiw P S,Watts R W.A mathematical model for the iron/chromium redox battery[J].J Electrochem Soc,1984,131(4):701-708.

[11]Evans T I,White R E.A mathematical model of a zinc/bromine flow cell[J].J Electrochem Soc,1987,134(4):866-874.

[12]Putt R A.Assessment of Technical and Economic Feasibility of Zinc/Bromine Batteries for Utility Load-Levelling[R].EPRIEM-1059,project 635-1,1979.

[13]Lee J,Selman J R.Effects of separator and terminal on the current distribution in parallel-plate electrochemical flow reactors[J].J Electrochem Soc,1982,129(8):1 670-1 678.

[14]Lee J.Effect of mass transfer on the current distribution and dendrite growth in electrochemical flow reactors[D].Chicago:Illinois Institute of Technology,1981.

[15]Mader M J,White R E.A mathematical model of a Zn/Br2cell on charge[J].J Electrochem Soc,1986,133(7):1 297-1 307.

[16]You D J,Zhang H M,Chen J.Theoretical analysis of the effects of operational and designed parameters on the performance of a flow-through porous electrode[J].J Electroanal Chem,2009,625(2):165-171.

[17]You D J,Zhang H M,Chen J.A simple model for the vanadium redox battery[J].Electrochim Acta,2009,54(27):6 827-6 836.

[18]Al-Fetlawi H,Shah A A,Walsh F C.Non-isothermal modeling of the all-vanadium redox flow battery[J].Electrochim Acta,2009,55(1):78-89.

[19]Shah A A,Al-Fetlawi H,Walsh F C.Dynamic modeling of hydrogen evolution effects in the all-vanadium redox flow battery[J].Electrochim Acta,2010,55(3):1 125-1 139.

[20]Al-Fetlawi H,Shah A A,Walsh F C.Modeling the effects of oxygen evolution in the all-vanadium redox flow battery[J].Electrochim Acta,2010,55(9):3 192-3 205.

[21]You D J,Zhang H M,Sun C X,et al.Simulation of the self-discharge process in vanadium redox flow battery[J].J Power Sources,2011,196(3):1 578-1 585.

[22]Xing F,Zhang H M,Ma X K.Shunt current loss in vanadium redox flow battery[J].J Power Sources,2011,196(24):10 753-10 757.

[23]Kaminski E A,Savinell R F.A technique for calculating shunt leakage and cell currents in bipolar stacks having divided or undivided cells[J].J Electrochem Soc,1983,130(5):1 103-1 107.

[24]White R E,Walton C W,Burney H S,et al.Predicting shunt currents in stacks of bipolar plate cells[J].J Electrochem Soc,1986,133(3):485-492.

[25]Burney H S,White R E.Predicting shunt currents in stacks of bipolar plate cells with conducting manifolds[J].J Electrochem Soc,1988,135(7):1 609-1 612.

[26]YOU Dong-jiang(尤東江).全釩液流儲能電池數學模型的研究[D].Beijing(北京):Graduate School of the Chinese Academy of Sciences(中國科學院研究生院),2010.