低速流場中的聲傳播模擬

倪大明，張文平，明平劍

(哈爾濱工程大學動力與能源工程學院，黑龍江哈爾濱150001)

計算氣動聲學已經成為預測聲產生和傳播的普遍工具［1］，其主要分為兩大類:1)是基于 Lighthill［2］聲比擬分析，結合聲源(單極子，雙極子，四極子)求解線性波動方程;2)是求解可壓縮的歐拉或N-S方程［3］.前者主要是在聲源和遠場建立關系，在其線性模型中反射、衍射以及一些非線性因素不被考慮，其主要用于預測聲場遠場，而后者考慮了非線性因素，但是由于計算資源的限制，模擬聲傳播很遠的距離計算量是很大的，因此，其主要被用于預測聲場近場.

對于高速流，Tam［4］提出了一種可壓縮歐拉和可壓縮N-S耦合的方法預測近場的聲產生和傳播.對于低速流，Hardin［5］在交錯網格的基礎上提出了二步法可預測聲產生和傳播，SHEN等在其基礎上在極坐標系下改進了二步法，并將其推廣到層流［6］和湍流［7］.對于均勻流場中的聲傳播問題，張榮欣等［8］采用切比雪夫譜元方法求解亞音速均勻流場中的輻射聲場，X.Nogueira等［9］在基于非結構化網格下提出了一種高精度有限體積法可以求解亞音速和超音速均勻流場中的輻射聲場.

基于非結構化網格，采用交錯網格計算比較復雜，因此，本文在直角坐標系下基于非結構化同位網格應用有限體積法結合SIMPLE算法模擬低速流中的聲傳播問題，在界面聲流速計算采用 Rhie-Chow［10］插值，在邊界上采用DRP(保持色散關系)吸收邊界，最后進行了算例的模擬并和聲學理論分析解進行了對比分析.

1 控制方程

可壓N-S方程組由連續方程、動量方程、絕熱等熵的狀態方程組成:

式中:ρ、u、p、c、S 分別為控制體中心的密度、速度矢量、壓力、聲傳播的速度和動量方程源項，ρ=ρ(x，y，z，t)，u=u(x，y，z，t)，p=p(x，y，z，t)，c=c(x，y，z，t).

對于低速流，不考慮聲反向散射對流場解的影響，將可壓N-S方程分解為流體動力項和擾動聲項，而流體動力項按照不可壓流場求解，用二步法將以上基本變量進行分解，則可壓變量:

式中:U是不可壓速度矢量;P是不可壓壓力;ρ0是不可壓密度;u'是聲擾動速度矢量;p'是聲擾動壓力;ρ'是聲擾動密度.

將式(4)代入方程(1)～(3)，并結合不可壓N-S方程，同時令矢量f=ρu'+ρ'U，則聲擾動方程的連續方程、動量方程和等熵狀態方程分別為

為了消除邊界反射對內部聲場的影響，采用DRP 無反射邊界［11］:

式中:un為可壓縮法向速度，r為邊界面中心到聲源距離，ui'為聲擾動速度分量，n對于一、二、三維問題分別取 0、1/2、1.

2 數值離散

不可壓流場和聲擾動場動量方程離散在時間項采用二階前差格式，對流項采用二階迎風格式，擴散項和壓力項采用中心差分.在求解界面不可壓流場流量和聲擾動場流量采用Rhie-Chow插值.不可壓流場求解應用明平劍［12］GTEA程序.

2.1 動量預測

根據動量方程(6)離散得到矢量f的離散方程:

式中:AP為計算單元中心矢量f的系數，Ai為計算單元鄰近單元中心矢量f的系數為計算單元中心矢量f的預測值為計算單元鄰近單元中心矢量f的預測值，V為計算單元體積.連續方程(5)離散得到:

式中:Σ f_f為單元界面上矢量f流量之和.

求解動量方程(9)，得到矢量f*，然后計算單元表面上的矢量f*流量:

2.2 壓力修正

引入矢量f修正量f'和聲壓修正量pp'，則f＊＊=f*+f'，p'＊＊=p'*+pp'，同時根據動量方程(9)，有:

式(13)與(9)相減，得到矢量f修正量f'更新公式:

同時結合連續方程(5)和絕熱狀態方程(7)，可得

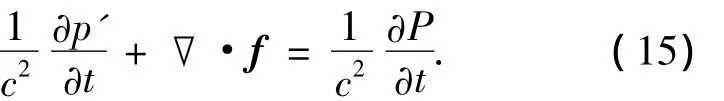
根據式(14)、(15)，可得聲壓力修正方程:

以上給出的SIMPLE算法以矢量形式給出，與具體坐標系及網格形式無關，適用于任意混合網格.

2.3 動量修正

聲壓修正后，根據式(14)更新矢量f值，其他變量按下式更新:

式中:u'i為聲擾動速度分量，fi為矢量變量分量，Ui為不可壓速度分量，Pref為環境參考壓力，γ為比熱，tref為環境參考溫度，上標n+1為當前時刻計算值，n為上個時刻值，n-1為上2個時刻值.值得注意的是:若流動介質可以作為完全理想氣體，則聲傳播速度按照式(19)更新;若流動介質為水，則聲傳播速度按照介質聲傳播速度經驗公式(20)更新.

3 求解步驟

圖1 系統工作流程Fig.1 Workflow of system

控制方程的求解包括不可壓流場和聲擾動場計算，如圖1所示，其求解步驟為:

1)根據上一個迭代層得到的U*、P*，以及上一個時間層的U0、P0，求解不可壓流場動量方程，得到新的U＊＊;

2)求解不可壓壓力修正方程，得到修正值P';

3)計算出新的P、U;

4)根據求出的P、U和上一個迭代層得到的矢量f*、聲擾動壓力p'*，以及上一個時間層的f0、p0'，求解聲擾動動量方程，得到新的f＊＊;

5)求解聲擾動壓力修正方程，得到修正值p″;

6)計算出新的 p'、f;

7)根據式(17)～(20)，更新 ρ'、ui'、c;

8)判斷迭代是否收斂，如果收斂，則進入下一個時間層，否則返回步驟1)繼續求解;

9)判斷時間是否已經達到設定值，如果達到則計算結束，反之，將目前值存入 U0、P0、p0'、f0、ρ0'、ui0'、c0，返回步驟1)，進入下一個時間層進行迭代.

4 均勻流場算例驗證

為了方便研究，本文采用具有解析解的單極子點聲源，其表達式如下:

式中:un'為聲源法向振動速度;A為聲源振幅;ω為角頻率.取 A=0.006，ω =68π.

4.1 流動對平面波傳播的影響

計算區域為Ω={(x，y):-25 m≤x≤25 m，-0.2 m≤y≤0.2 m}，在人工邊界 x=25 m 上面采用DRP吸收邊界條件，邊界x=-25 m給定點聲源，將計算區域劃分為400個非結構化網格，時間步長為 Δt=0.000 1 s，計算2 000 步.t=0.2 s時，沿 x軸的聲壓型線在Ma=0和0.2的對比見圖2.從圖2可以看出，Ma=0時，聲源波長為10 m;Ma=0.2時，聲源波長為12 m，其模擬結果符合聲傳播的多普勒效應，與理論分析吻合.同時可以看出，邊界處理較好，反射微小.

圖2 t=0.2 s，Ma=0，0.2 時沿 x 軸的聲壓型線對比Fig.2 Comparison of sound pressure distribution of numerical results on x axis，t=0.2 s，Ma=0，0.2

4.2 流動對柱面波傳播的影響

計算區域為Ω={(x，y)∶-50 m≤x≤50 m，-50 m≤y≤50 m}，在人工邊界?Ω上面采用DRP吸收邊界條件，點聲源位置坐標(0，0)，將計算區域劃分為8 861個非結構化網格.

取流場馬赫數 Ma=0，時間步長為 Δt=0.000 1 s，計算2 000步.可得到靜止流場中由單極子聲源產生的輻射聲場云圖，見圖3.沿x軸的聲壓型線與理論解析解的對比見圖4，可以看出，數值解和解析解吻合得良好.

圖3 Ma=0時的聲場云圖Fig.3 Distributions of sound pressure at different time，Ma=0

圖4 Ma=0時沿x軸的聲壓型線與理論解對比Fig.4 Sound pressure distributions of numerical results versus theoretics on x axis at different time，Ma=0

取流場馬赫數 ，其余參數不變，可得Ma=0.2流場中單極子聲源產生的聲場云圖見圖5，從圖6可以看出數值解與解析解吻合得很好，包括邊界條件的處理.

圖5 Ma=0.2時的聲場云圖Fig.5 Distributions of sound pressure at different time，Ma=0.2

圖6 Ma=0.2時沿x軸的聲壓型線與理論解對比Fig.6 Sound pressure distribution of numerical results versus theoretics on x axis at different time，Ma=0.2

5 圓柱繞流流噪聲模擬

計算區域為 Ω={(x，y)∶ -50 m≤x≤50 m，-50 m≤y≤50 m}，在人工邊界?Ω上面采用DRP吸收邊界條件，將計算區域劃分為25 421個非結構化網格.圓柱直徑為D=1 m，流場馬赫數Ma=0.2，雷諾數Re=200.時間步長為t=0.002 5 s，總計算時間為 t=3.75 s，當不可壓流場計算趨于周期變化時，即當t=2.5 s時，開始計算聲場，監測點設于坐標為(0 m，3 m)處.

若考慮圓柱表面有微小振動，為了方便研究，本文采用具有解析解的單極子聲源，其表達式見式(21).為了將流噪聲與該聲源區分開，取A=0.06，ω =68π.

當t=2.75 s時，聲場計算趨于穩定.取t=3 s時，半徑為r=3 m圓周上的聲壓值，繪制成聲壓指向性圖如圖7.從圖中可以看出，馬赫數為0.2時，圓柱繞流流噪聲的聲壓級處于81～123 dB之間，且沿著x軸對稱分布，最大聲壓級處于9°和-9°位置處.由于給定聲源的壓力輻值5 Pa小于流噪聲的壓力輻值38 Pa，因此給定聲源與流噪聲的干涉結果對圓柱上游影響較小，主要影響區域為圓柱上游區，其使流噪聲的聲壓級稍微有所增大.

圖7 圓柱表面是否微振指向性對比(r=3 m，t=3 s)Fig.7 Directivity pattern of circular cylinder noise radiation，considering circular cylinder surface slight shock or not，r=3 m，t=0.3 s

圖8 圓柱表面是否微振監測點聲壓隨時間變化對比Fig.8 Sound pressure distribution of moniter point vs time，considering circular cylinder surface slight shock or not

圖9 圓柱表面是否微振監測點聲壓隨頻率變化對比Fig.9 Sound pressure distribution of moniter point vs frequency，considering circular cylinder surface slight shock or not

觀察監測點聲壓隨時間變化如圖8，從圖中可以看出，單計算圓柱繞流流噪聲時，聲壓隨時間變化分布很規則，最大聲壓38 Pa，最小聲壓-26.5 Pa.通過FFT變換后，可得聲壓隨頻率變化如圖9，可以看出，圓柱繞流流噪聲主要集中在頻率為14 Hz處，可計算出斯特勞哈爾數:

其與聲學手冊中風吹聲斯特勞哈爾數一般為0.2相對應.

若模擬流噪聲與給定聲源相干涉問題，從圖8中可以看出，監測點的聲壓隨時間變化分布與單計算流噪聲的聲壓分布有明顯不同.通過FFT變換后，可得聲壓隨頻率變化如圖9，可以看出，噪聲主要集中在頻率為14 Hz和34 Hz處，14 Hz對應圓柱繞流流噪聲的主要集中頻率，而34 Hz對應給定聲源的頻率，其計算結果與理論分析吻合，進一步驗證了該方法的正確性和可靠性.

6 結束語

采用基于可壓N-S方程的分解法對低速流中的聲傳播問題進行數值模擬，并采用基于非結構化網格的有限體積法和SIMPLE算法求解不可壓流場方程的和聲擾動方程，在計算界面流速和聲擾動速度采用Rhie-Chow插值，在邊界上采用DRP吸收邊界條件消除邊界反射對聲場的影響.對低速流中平面波、柱面波、圓柱繞流流噪聲以及流噪聲與已知聲波干涉傳播問題進行了數值模擬，與理論分析解對比表明，這種數值模擬方法預測的聲傳播是穩定可靠的.由于非結構化網格的應用，該數值模擬方法可便捷求解結構復雜的低速流中的聲傳播問題.

［1］SHEN W Z，MICHELSEN J A，SORENSEN J N.A collocated grid finite volume method for aeroacoustic computations of low-speed flows［J］.Journal of Computational Physics，2004，196:348-366.

［2］LIGHTHILL M J.On sound generated aerodynamically.I:General theory［C］//Proceedings of the Royal Society A.London，1952.

［3］PHILIP J M，LYLE N L，ASHOK B，et al.A parallel threedimensional computational aeroacoustics method using nonlinear disturbance equations［J］.Journal of Computational Physics，1997，133:56-74.

［4］SHEN H，TAM C W.Numerical simulation of the generation of axisymmetric mode jet screech tones［J］.AIAA Journal，1998，36(10):1801-1828.

［5］HARDIN J C，POPE D S.An acoustic/viscous splitting technique for computational aeroacoustics［J］.Theoret Comput Fluid Dynamics，1994，6:323-340.

［6］SHEN W Z，SORENSEN J N.Aeroacoustic modeling of low-speed flows［J］.Theoret Comput.Fluid Dynamics，1999，13:271-289.

［7］SHEN W Z，SORENSEN J N.Aeroacoustic modeling of turbulent airfoil flows［J］.J AIAA，2001，39(6):1057-1064.

［8］張榮欣，秦國良.用切比雪夫譜元方法求解均勻流場中的聲傳播問題［J］.西安交通大學學報，2009，43(7):120-124.

ZHANG Rongxin，QIN Guoliang.Chebychev spectral elements method for acoustic propagation problem in a uniform mean flow［J］.Journal of Xi'an Jiaotong University，2009，43(7):120-124.

［9］NOGUEIRA X，COLOMINAS I，FELGUEROSO L C，et al.Resolution of computational aeroacoustics problems on unstructured grids with a higher-order finite volume scheme［J］.Journal of Computational and Applied Mathematics 2010，234(7):2089-2097.

［10］RHIE C M ，CHOW W L.Numerical study of the turbulent flow past an airfoil with trailing edge separation［J］.AIAA Journal，1983，21(11):1525-1532.

［11］TAM C M，WEBB J C.Dispersion-relation-preserving finite difference schemes for computational acoustics［J］.Journal of Computational Physics，1993，107:262-281.

［12］明平劍，張文平，雷國東，等.帶壁面射流燃燒室燃燒數值模擬［J］.航空動力學報，2008，23(7):1205-1211.

MING Pingjian，ZHANG Wenping，LEI Guodong，et al.Numerical simulation of combustion in a wall jet combustor［J］.Journal of Aerospace Power，2008，23(7):1205-1211.