基于改進D-S證據理論的水下航行器聲隱身性能評估

湯智胤，何 琳

(海軍工程大學 船舶與動力學院，振動與噪聲研究所，武漢 430033)

水下航行器的隱身性是水下航行器最基本的技術性能，其中聲隱身性能則是決定其隱身性的最重要因素。水下航行器的隱身安全性歷來被認為是頭等重要的問題［1］。傳統上，在中、低頻常采用有限元 +邊界元［2］;在高頻常采用統計能量法對殼體輻射聲計算［3］，以此判斷水下航行器的聲隱身性能。有限元+邊界元方法基本原理是用有限元方法描述彈性結構的振動問題，用邊界元方法來描述結構的聲輻射場，將有限元方法和邊界元方法在彈性結構與流體交界面上的離散化點相匹配，從而獲得結構與聲場的耦合運動方程。統計能量法是把研究對象劃分成子系統后，假定每個子系統的模態參數的統計分布為已知的統計母體，使用子系統的動力學能量來描述系統的狀態，利用能量變量就可使用簡單的功率流平衡方程來描述耦合子系統間的相互作用，使用能量變量統一處理結構、聲場等子系統間的相互作用問題［4］。雖然上述做法精度較高，但是速度慢，達不到快速計算的要求。實際應用中，對水下航行器隱身性需求，實時性要比精度更重要更具實戰效應。如何選擇合適而準確的方法，快速評估水下航行器聲隱身性是一項復雜而重要的問題。

現代先進的水下航行器上都安裝有包括力傳感器、速度傳感器、加速度傳感器等在內的大量傳感器。我們認為，對于該問題的工程解決方案，可以將數值計算問題變為基于多傳感器信息融合的模式識別問題來解決。即:不直接計算航行器輻射聲的具體大小，而是事先將航行器的聲隱身性分為有限的若干類;當航行器運行時，通過傳感器組采集的數據，將其聲隱身性歸為其中某一類，作為其聲隱身性評估結果。這樣一來，就將復雜的數值計算問題進行了合理簡化，滿足了實時性的要求。

1 模型的提出

傳統對水下航行器聲隱身性的評估，都是通過直接計算其輻射噪聲來實現。但水下航行器的復雜結構決定了其巨大的輻射噪聲計算量，實時性得不到保證。然而現代戰爭中，評估的實時性是水下航行器安全性的基本保證。實戰中若喪失了實時性，其聲隱身性評估則毫無意義。

多傳感器信息融合技術在近二三十年來取得了快速的發展。而其中D－S證據理論是處理不確定性問題時的一個有用的方法。它已廣泛用于信息融合和不確定性推理等領域，能在不需要先驗概率的情況下，以簡單的推理形式，得出較好的融合結果。

現代水下航行器上安裝數目最多的是殼體振動加速度傳感器(也稱加速度計)。本文避開水下航行器復雜的輻射聲計算而采用多傳感器信息融合的手段，直接利用布置在航行器殼體表面的多個加速度傳感器的實測時域信號，進行變換算出功率譜信號作為特征，然后用一種改進的D－S證據理論方法進行數據融合，提高了評估效率，能夠很好地解決水下航行器聲隱身性評估的實效性問題，從而實現水下航行器聲隱身性的快速評估。評估過程如圖1所示。

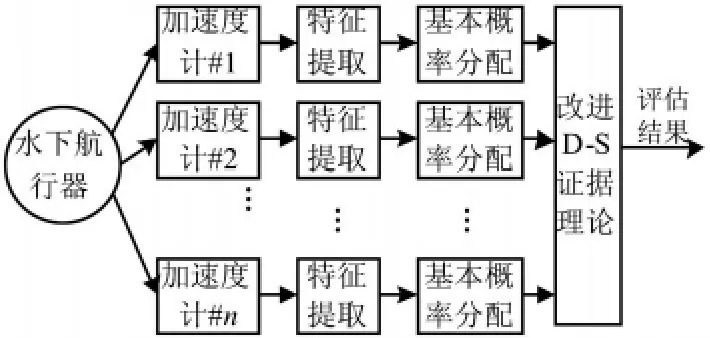
圖1 基于改進D－S證據理論的水下航行器聲隱身性能評估模型Fig.1 Acoustic stealth situation assessment model of underwater vehicle based on Improved D－S Theory

2 特征提取及基本概率分配

水下航行器輻射噪聲時，認為系統在大多數情況下都是線性的。航行器聲隱身性是其輻射噪聲決定的，而輻射噪聲又是航行器殼體振動所引起的。基于線形系統的假設，所以輻射噪聲所研究的頻段應與殼體振動研究的頻段一致。

2.1 特征提取

設殼體上有n個可用的振動加速度傳感器，水下航行器的輻射聲能量絕大部分集中于從fdown到fup頻率范圍內，其它頻段的能量很小。航行器聲隱身性能全部由這個頻段內的輻射噪聲所決定。基于系統線性假設，殼體振動的能量分布也在從fdown到fup頻率范圍內。取航行器殼體n個加速度傳感器的實測值，并分析從頻率fdown到fup之間的范圍。設從fdown到fup有r個點，計算出這些點的功率，并將其排列組成向量，作為水下航行器各傳感器振動加速度的特征向量。

2.2 基本概率分配函數

本文基本概率分配函數的確定方法為:將進行水下聲學實驗時所測各性能級別的所有傳感器數據作為基準，將實時測量的所有傳感器數據分別對其進行比較，計算出實測數據與基準數據間的距離，并對其進行歸一化處理，以此作為基本概率分配函數。具體步驟如下:

假設航行器聲隱身性能有L個級別，加速度傳感器共n個。將從fdown到fup的r個點，每個點的功率作為一維特征，即每個加速度傳感器測得的樣本可轉化為一個r維的特征向量。

設性能級別為l(l=1，2，…，L)時，加速度傳感器a(a∈{1，2，…，n})的基準特征向量為評估時刻，加速度傳感器a實測值的特征向量為:ap=［ap1，ap2，…，apr。將二者之間的距離記為。對于單個傳感器，計算出實測值的特征向量和所有性能基準向量的距離，并將歸一化處理的結果作為各性能下的基本分配函數值，即:am(l)=這里的距離將用到一種圖像歐式距離(Image Euclidean Distance)［5，6］:

設e1，e2，…，eR為對應R維空間的一組基向量，向量 p=［p1，p2，…，pR］T=p1e1+p2e2，…，pReR。圖像歐式距離IMED(image euclidean distance)定義為:

其中對稱矩陣 G=(gij)R×R稱為度量矩陣，gij(i，j=1，…，R)稱為度量系數定義為:

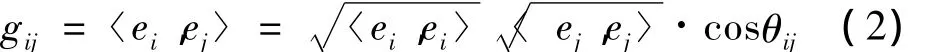
式中，〈，〉表示內積運算，θij是 ei和 ej間的夾角。常用的高斯函數所構造的圖像歐式距離為:

圖像歐式距離和傳統歐式距離的本質區別是:傳統歐式距離沒有考慮元素之間的空間關系，其基向量是完全獨立的。而圖像歐式距離則考慮了元素之間的空間關系，并體現在了度量系數中。

3 證據合成理論

由于其堅實的理論依據，D－S證據理論在很多情況下都能很好地進行信息融合，并得到與人們的直觀認識相一致的結果。但當證據源出現矛盾，甚至沖突時，D －S 證據理論合成公式將會失效［7－9］。

本文采用一種基于證據特征的證據合成規則［10，11］，進行水下航行器聲隱身性能評估。經計算仿真驗證，它要比傳統的Dempster證據合成規則和Yager證據合成規則的效果更好，結果也更符合實際解釋。對于識別框架Θ，整個空間的大小為2N，其子集記為:A1，A2，…，A2N。兩個證據m1和m2之間的距離為:

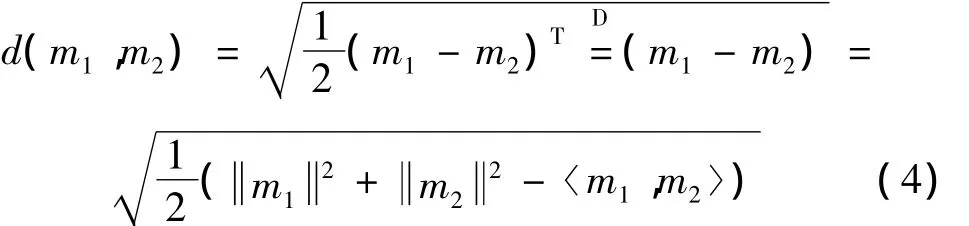
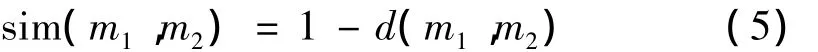
若有K個證據時，證據群體可靠性ε為:

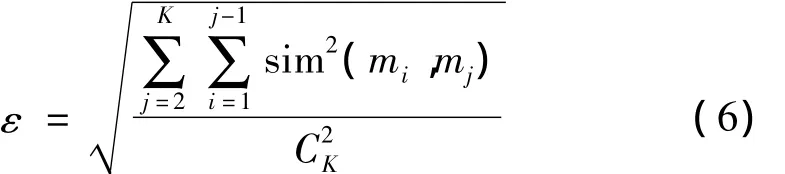
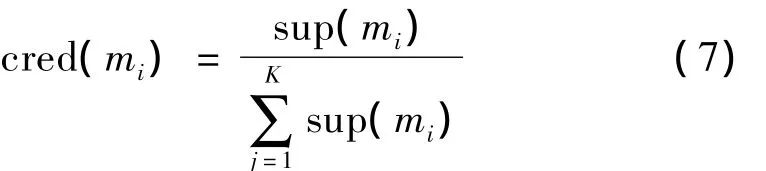
本文的證據合成規則，基于沖突信息可以利用，證據合成規則為:

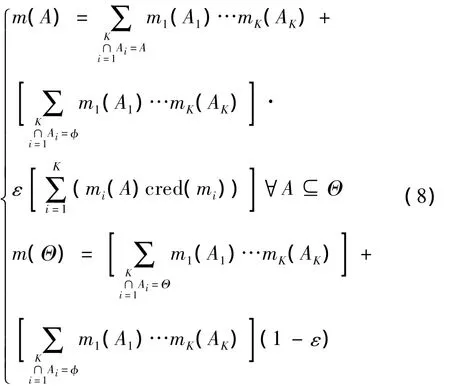
利用(8)式計算證據合成后的基本概率分配，分別求出所有狀態的信任函數Bel，比較所有狀態的信任函數值的大小，判定值最大的狀態為當前的航行器聲隱身性能級別。

4 應用實例分析

為測試方法的評估能力，我們進行以下仿真和實驗。

4.1 幾種距離的比較

比較兩種信號的歐式距離、Hausdorff距離和圖像歐氏距離的差異。

圖2～圖5中，紅色圖線表示的信號在4幅圖中是一樣的，藍色圖線代表的信號略有差異。

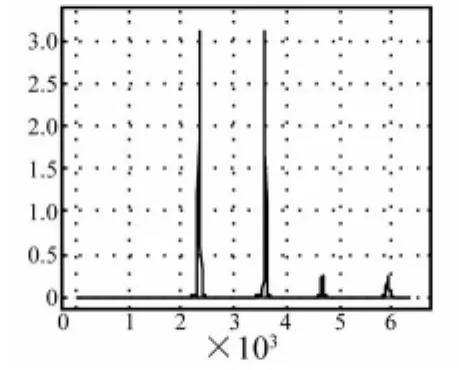
圖2 兩不同信號比較(1)Fig.2 Two different signals(1)

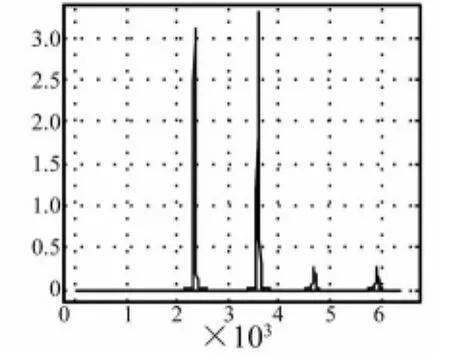
圖3 兩不同信號比較(2)Fig.3 Two different signals(2)

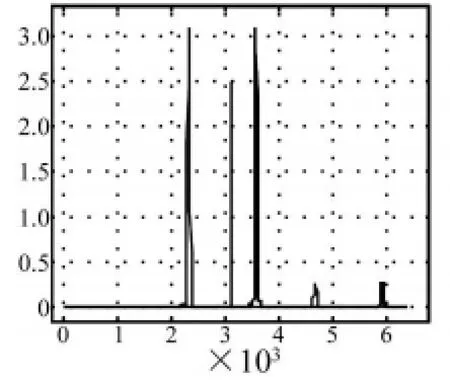
圖4 兩不同信號比較(3)Fig.4 Two different signals(3)

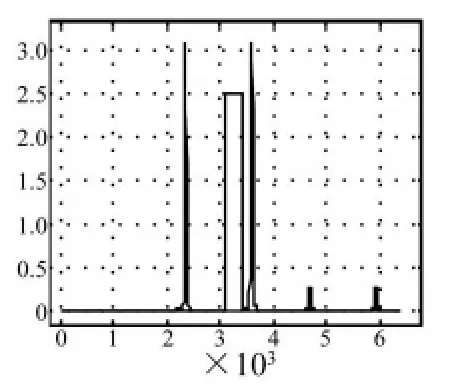
圖5 兩不同信號比較(4)Fig.5 Two different signals(4)

如圖2所示紅色和藍色兩個信號相比，僅有頻率的漂移，歐式距離 dE=9.9039，Hausdorff距離 dH=1.1418 ×10－5，圖像歐氏距離 dI=6.1631。當兩個信號在形狀上相似，而在位置上不同時，二者的Hausdorff距離比歐式距離和圖像歐氏距離都要小，圖像歐氏距離次之，歐式距離最大。

圖3和圖2相比，藍色信號僅有最大值點比原信號的最大值大5%，其歐式距離dE=9.9540，Hausdorff距離 dH=0.15570，圖像歐氏距離 dI=6.1929。其歐氏距離和圖像歐氏距離都與圖2中的相差不超過0.51%，而Hausdorff距離竟相差10982倍。

圖4中藍色信號比圖2中的多了一個尖峰，歐式距離 dE=10.214，Hausdorff距離 dH=0.017693，圖像歐氏距離dI=6.2433;圖5中藍色信號比圖2中多出的一部分方波，其峰值與圖4中的多出的尖峰峰值相等，歐式距離 dE=20.414，Hausdorff距離 dH=0.017693，圖像歐氏距離 dI=12.779。

比較圖4和圖5，兩圖中藍色信號的形狀差別相當大，而它們與紅色圖線的 Hausdorff距離相等，說明Hausdorff距離進行信號形狀比較時，主要是提取邊緣，然后再進行相似性度量，它對信號局部的變形也不是很敏感。而另一方面，如果噪聲對信號的極值造成影響，則有可能在計算Hausdorff距離時產生嚴重誤差。

歐氏距離雖然能很好地度量兩信號間的差異，對個別點的噪聲也不很敏感，但對于僅存在位置差異，而形狀相似的信號，卻不能很好的描述。

而圖像歐氏距離卻能兼顧歐式距離和Hausdorff距離之間的優點，對形狀相似的信號可以較好地度量，而對信號局部噪聲的敏感度也較小。

表1 圖2～圖4中兩信號的距離Tab.1 The distances between two signals in Fig.2 ～4

4.2 幾種證據合成方法的比較

假設有識別框架 Θ={A1，A2，A3}，5個證據源，分別是證據源 m1為:m1(A1)=0.98，m1(A2)=0.01，m1(A3)=0.01;m2為:m2(A1)=0.98，m2(A2)=0.01，m2(A3)=0.01;m3為:m3(A1)=0，m3(A2)=0.99，m3(A3)=0.01;m4為:m4(A1)=0.98;m4(A2)=0.01，m4(A3)=0.01;m5為:m5(A1)=0.98;m5(A2)=0.01，m5(A3)=0.01。這5個證據源可以代表這樣的情況:所有傳感器對狀態都是A1都是較大程度地支持，(有可能是故障或較強的局部噪聲所導致的)僅有一個傳感器m3對A1進行了全部否定，而較大程度地支持了A2。觀察表2的證據合成結果，發現經典的證據合成方法在m2出現之前，三種方法的合成結果差別不大。而當m3出現之后，三種方法出現了顯著的差別:由于m3對A1的全部否定，造成即使后面所有的證據都支持A1，用D－S證據合成方法，m(A1)始終為0，并將較大程度的支持分配給A2;而用Yager證據合成方法m(A1)也是始終為0，m(A2)和m(A3)也都隨著證據源的個數增大而不斷減小，并將絕大多數的支持全部分配給了全域。這兩種合成結果顯然是與實際常理相違背的。而用本文的證據合成方法，即使出現了一個與大多數正確證據源相沖突的錯誤證據源，合成結果也會隨著正確證據源個數的增大而逐漸收斂到合理的結果，降低了錯誤證據源對信息融合結果的影響。

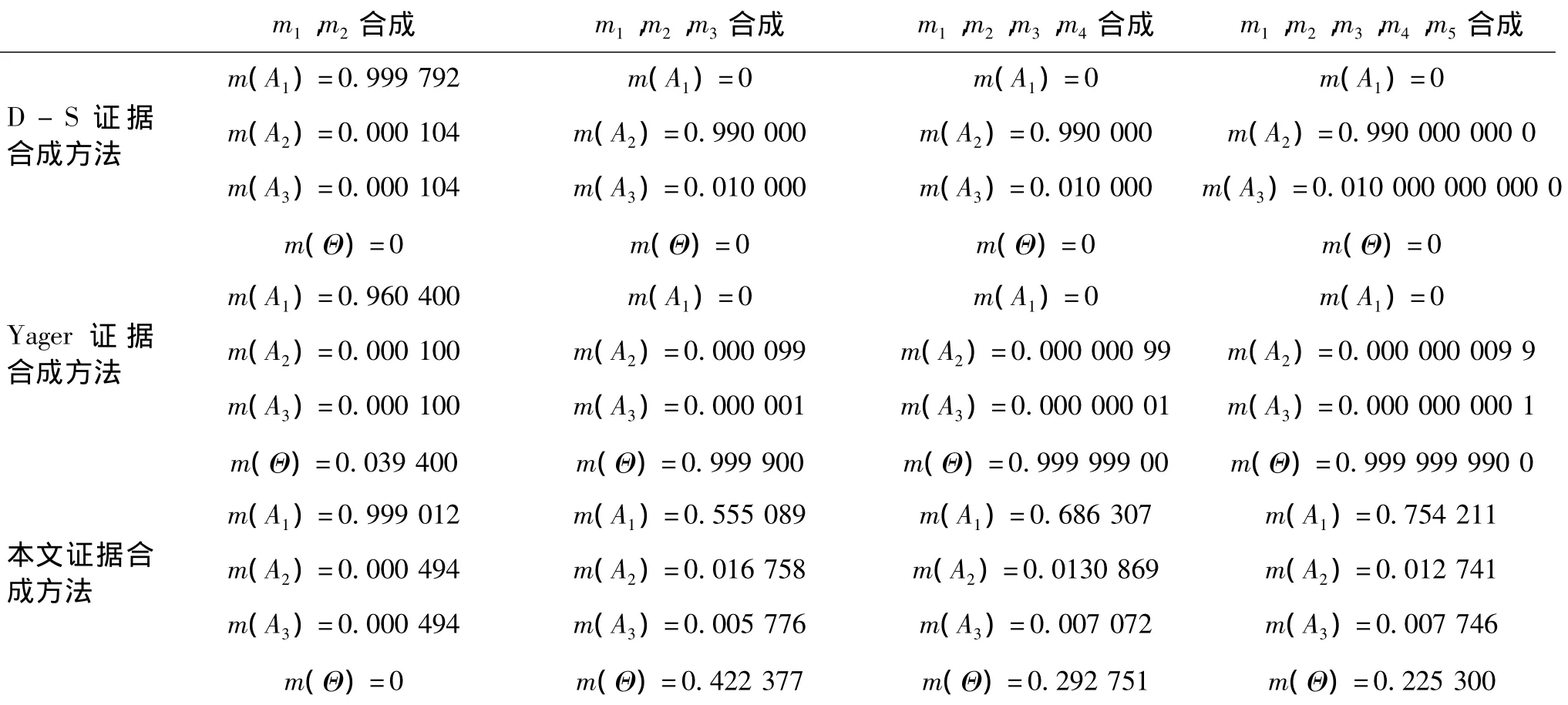
表2 不同證據合成公式對比Tab.2 Different results based on different evidence theories

4.3 不同個數證據源合成結果的比較

利用鐵制雙層加肋圓柱殼體進行水下聲學實驗。殼體外直徑560mm，內直徑400mm，高600mm。殼體內部安裝3個激振器，模擬航行器內部機械裝置對艇體的激勵，在殼體表面上布置15個加速度傳感器。根據模型的對稱性，在內殼體內部布置3個激勵點和10個加速度傳感器，外殼體外表面布置17個加速度傳感器。其布置方式如圖6所示。表面加蓋并密封，置于深約70 m，面積約250 m×1000 m的水庫中;殼體布放位置離岸最近60 m，頂部離水面1.7 m;離殼體表面1m處，懸垂一個水聽器，如圖7所示。

實驗設備為:

(1)信號發生器:用DP測量系統產生2路信號，用信號發生器產生1路信號;

(2)功率放大器2個:YE2706、YE5872;

(3)電磁激振器3臺:JZK－2兩臺、JZK－20一臺;

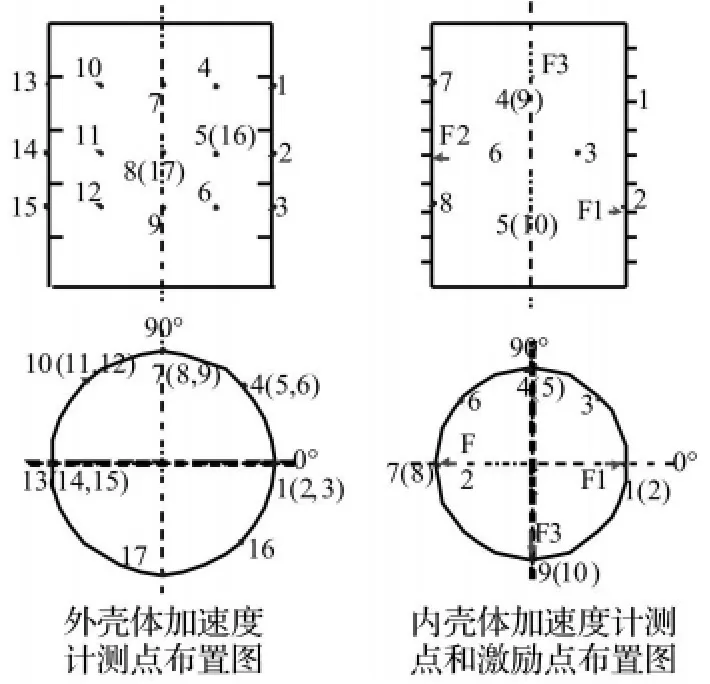
圖6 內外殼體激勵點、加速度測點布置圖Fig.6 Position of vibration points ＆ Accelerometers

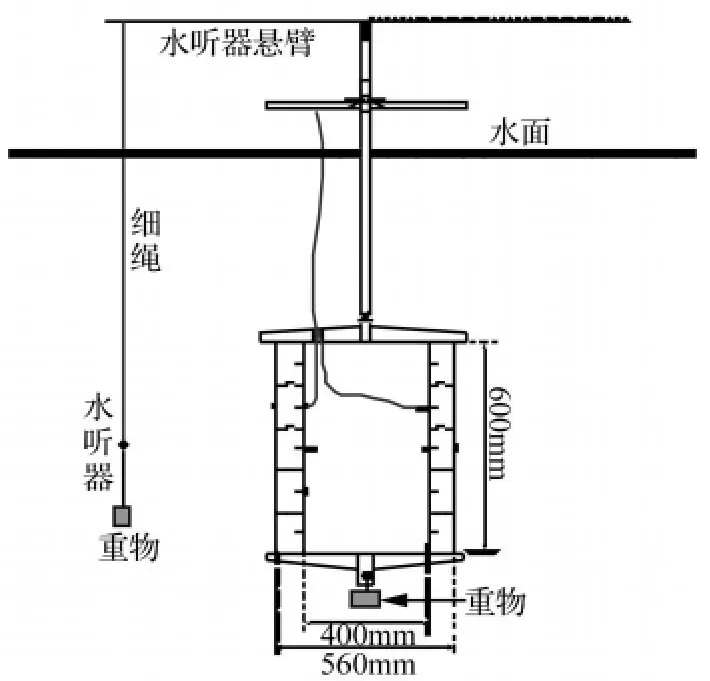
圖7 雙層圓柱殼體水下試驗安裝示意圖Fig.7 Installation drawing of the equipment

(4)電荷放大器2個(信號放大、帶通濾波);

(5)加速度傳感器27個(內10外17):ICP加速度傳感器(KD1002LC);

(6)32通道采集調理設備;

進行水下實驗時，用殼體內部的電磁激振器激勵殼體振動，測量內外殼體表面上的加速度信號。激勵工況有單點激勵，雙點組合激勵和三點同時激勵;激勵信號有白噪聲和單頻穩態正弦信號。實驗采樣頻率為6400Hz，采樣時間 4 s，聲壓基準值為 1 μPa。

評估時可將其聲隱身狀態分為:n類，n的取值可根據需要來定。不失一般性，本文中取n=3，分別對應#1、#2、#3激振器的激勵情況。每個狀態選擇9個工況進行評估。評估時隨機選取不同個數的傳感器，用三種不同距離形成證據，并用本文中的改進D－S證據合成方法進行證據合成，比較評估正確率，結果如表3所示。

從表3中，我們可以發現雖然利用圖像歐氏距離產生的證據能達到最大的正確率，但是與直觀認識相矛盾的是證據源個數和評估正確率之間沒有明顯的規律。而且利用內殼傳感器信息的識別正確率，不一定比用外殼傳感器的正確率低。這是因為證據理論的基礎是基于大多數證據都是支持正確命題的假設。然而實際中并不是完全符合這一假設，所以對證據源的選擇，即傳感器數據的選取方法還需要進一步地研究。

另一方面，用三種距離的識別方法其計算時間都會隨著證據源個數的增大而增大。當選用10個內殼傳感器和17個外殼傳感器時，時間最長:用歐式距離最長計算時間7 s以內;用Hausdorff距離最長計算時間520 s;用圖像歐氏距離最長計算時間316 s。如果要將此方法應用到實際中，傳感器個數將是數以百計，計算時間也會成倍增長。但即使如此，也比傳統輻射噪聲計算方法的時間要短得多。

表3 不同個數傳感器信息融合結果對比Tab.3 Different results based on different number of accelerometers

5 結論

本文針對以往水下航行器輻射聲計算方法中計算時間長、實時性差、達不到作戰使用要求的缺點，通過用圖像歐氏距離進行傳感器證據生成，以及一種改進的D－S證據合成方法相結合，提出了一種新的水下航行器聲隱身性能快速評估方法。并利用仿真和實驗相結合的方式，比較了本文方法和傳統方法的差異。該評估方法計算速度較快、評估正確率較高、通用性較強，可應用于各類結構的聲學狀態評估，一定程度上為作戰使用提供了技術支持。

然而該方法還需進一步改進的地方:對于不同位置的傳感器，其評估正確率差別都相當大。所以在使用中，需要結合實際航行器結構進行傳感器安裝位置的研究;對于已安裝好傳感器的航行器，在選用傳感器時還需要進行篩選，盡量用少的傳感器信息得到較高的評估正確率，從而滿足實時性和有效性的平衡。

［1］湯智胤，姜榮俊，何 琳.潛艇聲隱身態勢評估方法研究［J］.武漢理工大學學報(交通科學與工程版)，2007，31(1):17－20.

［2］彭 旭，駱東平.船舶結構建模及水下振動和輻射噪聲預報［J］.噪聲與振動控制，2003，23(6):9－12.

［3］伍先俊，朱石堅.統計能量法及其在船舶聲振預測中的應用綜述［J］.武漢理工大學學報(交通科學與工程版)，2004，28(2):212－215.

［4］姚德源，王其政.統計能量分析原理及其應用［M］.北京:北京理工大學出版社，1995，175(4－5).

［5］Wang L，Zhang Y，Feng J.On the euclidean distance of images［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27(8):1334－1339.

［6］封舉富，王立威.圖像空間中的距離［M］.北京:清華大學出版社，2007.

［7］楊曉明，譚永紅，蘇密勇.D－S證據理論合成規則的一些修正［J］桂林電子工業學院學報，2004，24(1):13－16.

［8］Zadeh L A.Review of Shafer＇s A Mathematical Theory of Evidence［J］，AI Magazine，1984，5:81 －83.

［9］Yager R.On the Dempster Shafer framework and new combination rules ［J］. InformationSciences，1987(41):93－137.

［10］Jousselme A L ，Grenier D，Bossé E.A new distance between two bodies of evidence［J］.Information Fusion，2001(2):91－101.

［11］杜 鋒，施文康，鄧 勇.證據特征提取及其在證據理論改進中的應用［J］.上海交通大學學報(增刊)，2004(38):164－168.