基于均勻圓陣的近場(chǎng)源三維參數(shù)估計(jì)

胡增輝 朱炬波 何 峰 梁甸農(nóng)

（1.國(guó)防科學(xué)技術(shù)大學(xué)電子科學(xué)與工程學(xué)院，湖南 長(zhǎng)沙 410073；2.國(guó)防科學(xué)技術(shù)大學(xué)理學(xué)院，湖南 長(zhǎng)沙 410073；3.酒泉衛(wèi)星發(fā)射中心，甘肅 酒泉 732750）

1.引 言

與均勻線陣（ULA）相比，均勻圓陣（UCA）具有許多優(yōu)異的特性，如能同時(shí)估計(jì)信號(hào)的方位角和俯仰角、測(cè)向精度隨方位角變化不明顯等。基于均勻圓陣的波達(dá)參數(shù)估計(jì)一直是陣列信號(hào)處理領(lǐng)域的研究熱點(diǎn)。

目前，基于均勻圓陣的波達(dá)參數(shù)估計(jì)算法［1－4］的研究主要集中在二維波達(dá)角估計(jì)上，即方位角和俯仰角的估計(jì)。然而，當(dāng)源信號(hào)位于圓陣的Fresnel區(qū)域［5］內(nèi)時(shí)，遠(yuǎn)場(chǎng)條件下的平面波前假設(shè)不再成立。在此情形下，除方位角和俯仰角外，源信號(hào)到圓陣的距離也需要估計(jì)。然而，到目前為止，基于均勻圓陣的近場(chǎng)參數(shù)估計(jì)算法非常少。LEE［6］等人利用路徑跟蹤技術(shù)，提出了一種近場(chǎng)源三維參數(shù)估計(jì)算法。該算法首先利用二維多重信號(hào)分類(lèi)（MUSIC）算法，得到方位角和俯仰角的初始估計(jì)，然后利用路徑跟蹤技術(shù)，多次搜索得到距離、方位角和俯仰角的聯(lián)合估計(jì)。然而，二維MUSIC算法需要進(jìn)行二維頻域搜索，計(jì)算量非常大，且其估計(jì)精度受搜索步長(zhǎng)的影響。

高階累積量［7－8］在空間譜估計(jì)中有著廣泛的應(yīng)用，它能夠抑制高斯噪聲。在文獻(xiàn)［6］算法結(jié)論的基礎(chǔ)上，提出一種基于高階累積量矩陣聯(lián)合對(duì)角化［9－10］的均勻圓陣近場(chǎng)源三維參數(shù)估計(jì)算法，該算法無(wú)需進(jìn)行二維頻域搜索。

2.理論分析

首先介紹相關(guān)信號(hào)模型及假設(shè)條件，然后構(gòu)造一組高階累積量矩陣，通過(guò)累積量矩陣聯(lián)合近似對(duì)角化得到陣列流形矩陣的估計(jì)。利用陣列流形矩陣的估計(jì)及文獻(xiàn)［6］的結(jié)論，首先得到方位角的精確估計(jì)和距離、俯仰角的粗略估計(jì)。為提高估計(jì)精度，利用最小二乘方法來(lái)獲得更高精度的估計(jì)。

2.1 信號(hào)模型

考慮由N個(gè)各向同性陣元組成的均勻圓陣（如圖1所示），以均勻圓陣所在的平面為x－y平面，圓陣圓心為坐標(biāo)原點(diǎn)，圓陣半徑為R.M個(gè)具有相同中心頻率fc的獨(dú)立近場(chǎng)窄帶信號(hào)入射陣列，入射參數(shù)為（rk，θk，φk），k＝1，…，M.為避免模糊，通常假設(shè)θk∈［0，π／2），φk∈［0，2π）.

圖1 均勻圓陣結(jié)構(gòu)示意圖

以坐標(biāo)原點(diǎn)處的虛擬陣元為相位參考點(diǎn)，t時(shí)刻第i個(gè)陣元的輸出為

式中：sk（t）為第k個(gè)源信號(hào)；ni（t）表示第i個(gè)陣元上的加性高斯白噪聲；ai（rk，θk，φk）為第k個(gè)源信號(hào)對(duì)應(yīng)的導(dǎo)向矢量a（rk，θk，φk）的第i個(gè)元素：

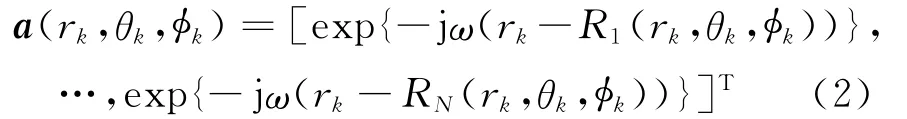
式中：ω＝2π／λ，λ為信號(hào)的載波波長(zhǎng)，上標(biāo)T表示向量和矩陣的轉(zhuǎn)置，Rl（rk，θk，φk）為第k個(gè)源信號(hào)到第l個(gè)陣元的距離，且有

其中ρl（θk，φk）＝sinθkcos（φk－（l－1）θ0），l＝1，…，N，θ0＝2π／N.

對(duì)于近場(chǎng)源，利用 Fresnel近似，Rl（rk，θk，φk）可以近似為

式（1）用矩陣形式表示為

式中：x（t）＝ ［x1（t），…，xN（t）］T為接收信號(hào)矢量；A＝ ［a（r1，θ1，φ1），…，a（rM，θM，φM）］為陣列流形矩陣；s（t）＝ ［s1（t），…，sM（t）］T和n（t）＝ ［n1（t），…，nN（t）］T分別為源信號(hào)矢量和噪聲矢量。

對(duì)信號(hào)模型作如下假設(shè)：

1）源信號(hào)是相互統(tǒng)計(jì)獨(dú)立的窄帶平穩(wěn)隨機(jī)過(guò)程，它們的四階累積量均不為零。

2）陣元上的加性噪聲是零均值白高斯過(guò)程，噪聲與信號(hào)之間是相互統(tǒng)計(jì)獨(dú)立的。

3）N≥M，陣列流形矩陣A是列滿秩的。

4）相鄰陣元間距d和載波波長(zhǎng)λ之間滿足如下關(guān)系：d≤λ／2.

假設(shè)2）～4）為近場(chǎng)源參數(shù)估計(jì)問(wèn)題的一般性假設(shè)，而假設(shè)1）則是基于高階累積量的算法所通常需要的假設(shè)條件。另外，源信號(hào)數(shù)目M的確定屬于信號(hào)檢測(cè)問(wèn)題，已有許多文獻(xiàn)研究該問(wèn)題，因此，假設(shè)M是已知的。

2.2 陣列流形矩陣A的估計(jì)

定義陣元接收數(shù)據(jù)的四階累積量［9］

式中：表示標(biāo)量xi的共軛；xH表示矢量x的轉(zhuǎn)置共軛；E｛x｝表示隨機(jī)變量x的期望。

由式（5）及假設(shè)H1和H2，Ci具有如下形式

式中：Γi＝diag｛cs1｜A（i，1）｜2，…，csM｜A（i，M）｜2｝，diag｛z1，z2｝表示以z1和z2為對(duì)角線元素的對(duì)角矩陣，csi＝cum｛，si｝為源信號(hào)si（t）的四階累積量；A（i，k）表示A的第i行第k列元素。

由于A是滿秩的，對(duì)任意的1≤i≠k≤M，至少存在m∈ ｛1，...，N｝，使得Γm的第i個(gè)和第k個(gè)對(duì)角線元素不相同。因此，可以應(yīng)用矩陣聯(lián)合對(duì)角化技術(shù)到來(lái)得到A的估計(jì)。

矩陣聯(lián)合對(duì)角化是指，尋找滿足一定約束條件（如范數(shù)為某個(gè)常數(shù)）的非零矩陣V，使得式（8）定義的代價(jià)函數(shù)值最小。

式中off｛B｝表示矩陣B非對(duì)角線元素絕對(duì)值平方和。

文中利用文獻(xiàn)［11］中的非正交聯(lián)合對(duì)角化算法得到A的估計(jì)。

理想情況（無(wú)噪聲，源信號(hào)之間嚴(yán)格統(tǒng)計(jì)獨(dú)立）下，A的估計(jì)與A之間滿足

式中：Λ為一對(duì)角線元素非零的對(duì)角矩陣，代表估計(jì)的尺度不確定性；P為一置換矩陣，代表順序不確定性。

置換矩陣P對(duì)于結(jié)果的影響可以忽略。因?yàn)锳每列可由一組不完全相同的（r，θ，φ）表示。得到后，由~A的每列可得到一組（r，θ，φ）的估計(jì)。因此，后文不考慮P的影響，即假設(shè)

2.3 方位角估計(jì)

文獻(xiàn)［6］指出，無(wú)論距離和俯仰角取值如何，近場(chǎng)方位角等于距離無(wú)窮遠(yuǎn)時(shí)的方位角。因此，利用該結(jié)論及已有的遠(yuǎn)場(chǎng)均勻圓陣二維波達(dá)角估計(jì)算法，結(jié)合式（10）的~A，可以首先得到較為精確的方位角估計(jì)。

令Λ＝diag｛λ1，...，λM｝，記的第k列為則

定義 （N－1）×1維矢量bk（l）＝（l＋1）／（l），將式（11）及式（2）代入bk的定義式中可得

由文獻(xiàn)［6］的結(jié)論，令rk→∞，由于ω｜（Rl＋1（rk，θk，φk）－Rl（rk，θk，φk）｜≤2πd／λ≤π，因此，由式（12）可以得到

式中arg｛·｝表示相位算子，其取值范圍為［－π，π］.將式（13）用矩陣表示為

式中η＝ ［sinθksinφk，sinθkcosφk］T

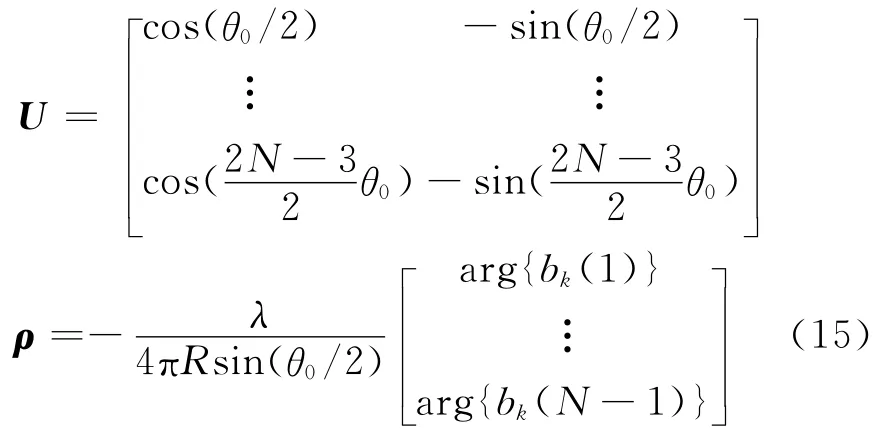
利用線性最小二乘，由式（14）可得η的估計(jì)，記為＝（UHU）－1UHρ。由可得到方位角φk的估計(jì)為

2.4 距離和俯仰角估計(jì)

由2.3節(jié)的討論知，利用的每列可以得到一個(gè)方位角的估計(jì)。本節(jié)，利用以及方位角的估計(jì)，對(duì)距離和俯仰角進(jìn)行估計(jì)。

對(duì)的第k列，由式（12）和（13）有

將式（4）代入式（17）可得

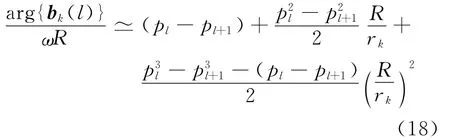
式中：pl＋1＝pl＋1（θk，φk）；pl＝pl（θk，φk）.

令αk（l）＝cos（φk－（l－1）θ0）－cos（φk－lθ0），γk＝arg｛bk（l）｝／（ωR），yk＝sinθk，zk＝R／rk，βk（l）＝cos（φk－（l－1）θ0）＋cos（φk－lθ0），式（18）可以簡(jiǎn)化為

式（19）用矩陣表示為

式中：

由式（20）和0≤θk＜π／2，以及源信號(hào)位于圓陣的Fresnel區(qū)域內(nèi)的約束條件，利用線性最小二乘方法可以求得（rk，θk）的估計(jì)值，記為）。估計(jì)過(guò)程中，將由式（16）得到的代替φk.

綜上所述，由的每一列，可得到某個(gè)源對(duì)應(yīng)的波達(dá)參數(shù)（rk，θk，φk）的估計(jì)（）.

由式（11）～（22）可得到波達(dá)參數(shù)的粗略估計(jì)。然而，通常情況下，距離和俯仰角的估計(jì)精度可能不是很高，原因可能是多方面的

1）Fresnel近似誤差可能非常小，但傳播到每個(gè)參數(shù)上的誤差可能非常大；

2）矩陣A的估計(jì)存在一定的誤差；

3）即使方位角φ的估計(jì)精度很高，由式（20）估計(jì)（r，θ）時(shí)，φ的微小誤差也可能被放大。

對(duì)A的估計(jì)的第l列，利用（rl，θl，φl(shuí)）的初始估計(jì)（），（rl，θl，φl(shuí)）可由如下的約束最小值問(wèn)題重新估計(jì)，即

式中f（rl，θl，φl(shuí)）稱(chēng)為殘差函數(shù)，其定義為

其中bl定義見(jiàn)式（12），d定義為

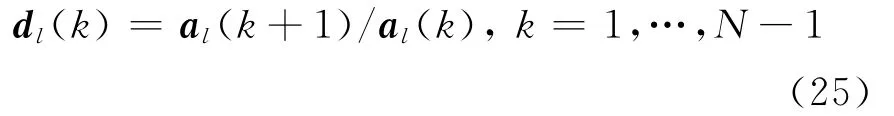
式（23）為典型的約束非線性最小二乘問(wèn)題，可應(yīng) 用 經(jīng) 典 的 Gauss－Newton 或 Levenberg－Marquardt等算法［12］進(jìn)行求解，由式（11）～（22）估計(jì)得到的（）作為迭代初值。由于迭代初值與真值誤差（尤其是方位角）不是非常大，通常迭代幾步即可得到收斂值。

3.實(shí)驗(yàn)結(jié)果分析

本節(jié)通過(guò)仿真實(shí)驗(yàn)驗(yàn)證所提算法的有效性，并將文中算法與文獻(xiàn)［6］中算法進(jìn)行比較，文獻(xiàn)［6］中算法簡(jiǎn)記為MUSIC－PF.

實(shí)驗(yàn)結(jié)果為500次Monte－Carlo實(shí)驗(yàn)的平均數(shù)據(jù)，分別采用均方根誤差（RMSE）和歸一化均方根誤差（NRMSE）作為角度（方位角和俯仰角）和距離的估計(jì)精度衡量指標(biāo)。

仿真1 研究信噪比（SNR）對(duì)波達(dá)參數(shù)估計(jì)精度的影響。源信號(hào)選為si（t）＝exp（j（0.2πt＋φi）），其中φi為［0，2π］內(nèi)的均勻分布，φi間相互獨(dú)立。均勻圓陣由13個(gè)陣元組成，圓陣半徑R＝λ，相鄰陣元間距約為0.48λ.兩個(gè)源信號(hào)的波達(dá)參數(shù)分別為（2.5R，30°，45°）和 （3R，50°，70°），采樣數(shù)為 1024。SNR從5dB變化到25dB時(shí)，角度估計(jì)RMSE和距離估計(jì)NRMSE隨SNR的變化曲線如圖2所示。MUSIC－PF算法中，二維MUSIC算法搜索步長(zhǎng)為0.05°.

由圖2可以看到，無(wú)論是角度估計(jì)還是距離估計(jì)，本文算法性能都要優(yōu)于MUSIC－PF算法。原因主要有兩個(gè)：一是MUSIC－PF算法方位角估計(jì)誤差相對(duì)較大，進(jìn)而影響距離和俯仰角估計(jì)精度；二是本文算法為高階累積量算法，它能抑制高斯白噪聲。

仿真2 考慮采樣數(shù)對(duì)參數(shù)估計(jì)精度的影響。仿真條件同仿真1，SNR＝15dB，采樣數(shù)從128變化到1024。圖3為本文算法和MUSIC－PF算法參數(shù)估計(jì)性能隨采樣數(shù)的變化曲線。由圖3可以看到，MUSIC－PF算法對(duì)采樣數(shù)不是很敏感。當(dāng)采樣數(shù)較少時(shí)，本文算法性能比 MUSIC－PF算法差，而當(dāng)采樣數(shù)較多時(shí)，情況則正好相反。主要原因在于MUSIC－PF算法利用的是二階統(tǒng)計(jì)量，它對(duì)采樣數(shù)不是非常敏感。而本文采用的四階累積量雖然能抑制高斯白噪聲，但是它對(duì)采樣數(shù)比較敏感。

4.結(jié) 論

基于均勻圓陣，提出了一種基于高階累積量的近場(chǎng)源距離－方位角－俯仰角估計(jì)算法。首先利用陣元接收數(shù)據(jù)構(gòu)造一組高階累積量矩陣，通過(guò)矩陣聯(lián)合對(duì)角化技術(shù)得到陣列流形矩陣的估計(jì)。再利用近場(chǎng)和遠(yuǎn)場(chǎng)情形方位角相同的結(jié)論，得到方位角的估計(jì)。最后利用估計(jì)得到的陣列流形矩陣及方位角，得到距離和俯仰角的估計(jì)。為提高估計(jì)精度，利用非線性最小二乘重新估計(jì)波達(dá)參數(shù)。與文獻(xiàn)［6］中算法相比，本文算法無(wú)需進(jìn)行二維頻域搜索，且在采樣數(shù)比較多時(shí)參數(shù)估計(jì)精度更高。本文算法的高估計(jì)性能代價(jià)是計(jì)算量比較大，主要是由于高階累積量計(jì)算及矩陣聯(lián)合對(duì)角化。

圖3 角度估計(jì)RMSE和距離估計(jì)NRMSE隨采樣數(shù)變化曲線

［1］MATHEWS C P，ZOLTOWSKI M D.Eigenstructure techniques for 2－D angle estimation with uniform circular arrays ［J］.IEEE Transactions on Signal Processing，1994，42（9）：2395－2407.

［2］陶建武，石要武，常文秀.一般陣列誤差情況下信號(hào)二維方向角估計(jì) ［J］.電波科學(xué)學(xué)報(bào)，2006，21（4）：606－611.

TAO Jianwu，SHI Yaowu，CHANG Wenxiu.Estimation of 2Dangle for signals with general array error［J］.Chinese Journal of Radio Science，2006，21（4）：606－611.

［3］熊維族.一種盲的多個(gè)分布源到達(dá)方向估計(jì)算法［J］.電波科學(xué)學(xué)報(bào)，2008，23（5）：942－945.

XIONG Weizu.A blind DOA estimation algorithm for multiple spread sources［J］.Chinese Journal of Radio Science，2008，23（5）：942－945.

［4］YE Z，XIANG L，XU X.DOA estimation with circular array via spatial averaging algorithm ［J］.IEEE Antennas Wireless Propagation Letters，2007，6（1）：74－76.

［5］HOOLE P R P.Smart Antennas and Signal Processing for Communications，Biomedical and Radar Systems［M］.Southampton：WIT Press，2001.

［6］LEE J H，PARK D H，PARK G T，et al.Algebraic path－following algorithm for localizing 3－D near－field sources in uniform circular array ［J］.Electronics Letters，2003，39（17）：1283－1285.

［7］MENDEL J M.Tutorial on high order statistics（spectra）in signal processing and system theory：theoretical results and some applications［C］∥ Proc.of IEEE，1991，79（3）：278－305.

［8］DOGAN M C，MENDEL J M.Application of cumulants to array processing part II：non－Gaussian noise suppression［J］.IEEE Transactions on Signal Processing，1995，43（7）：1663－1676.

［9］周 祎，馮大政，劉建強(qiáng).基于聯(lián)合對(duì)角化的近場(chǎng)源參數(shù)估計(jì) ［J］.電子與信息學(xué)報(bào)，2006，28（10）：1766－1769.

ZHOU Yi，F(xiàn)ENG Dazhen，LIU Jianqiang.Parameter estimation of near field sources using joint diagonalization［J］.Journal of Electronics and Information Technology，2006，28（10）：1766－1769.

［10］夏鐵騎，萬(wàn) 群，游志軍，等.沖擊噪聲環(huán)境中的聯(lián)合對(duì)角化波達(dá)方向矩陣法 ［J］.電波科學(xué)學(xué)報(bào)，2008，23（3）：460－465.

XIA Tieqi，WAN Qun，YOU Zhijun，et al.Joint diagonalization DOA matrix method in impulsive noise environments［J］.Chinese Journal of Radio Science，2008，23（3）：460－465.

［11］LI X L，ZHANG X D.Nonorthogonal joint diagonalization free of degenerate solution［J］.IEEE Transactions on Signal Processing，2007，55（5）：1803－1814.

［12］NOCEDAL J，WRIGHT S J.Numerical Optimization［M］.New York：Springer－Verlag Press，1999：250－275.