含非貫穿直裂紋管道的振動(dòng)特性分析

胡家順，馮 新，周 晶

(1.中國(guó)石油集團(tuán)安全環(huán)保技術(shù)研究院 安全技術(shù)研究所，北京 100083;2.大連理工大學(xué) 海岸和近海工程國(guó)家重點(diǎn)試驗(yàn)室，大連 116024)

在交變荷載的長(zhǎng)期作用下，裂紋的萌生和擴(kuò)展導(dǎo)致結(jié)構(gòu)抗力衰減，甚至引起結(jié)構(gòu)的破壞和倒塌。近年來(lái)，裂紋結(jié)構(gòu)的振動(dòng)分析、裂紋診斷受到了普遍關(guān)注，已成為研究熱點(diǎn)之一［1－10］。荷載作用下，結(jié)構(gòu)裂紋尖端附近區(qū)域出現(xiàn)應(yīng)變能集中，引起了局部柔度的變化。Irwin［3］使用等效彈簧的概念從宏觀上量化荷載與裂紋尖端應(yīng)力集中的關(guān)系，通過(guò)測(cè)量裂紋梁局部柔度描述應(yīng)力強(qiáng)度集中，成為早期試驗(yàn)確定應(yīng)力強(qiáng)度因子的標(biāo)準(zhǔn)方法，推動(dòng)了含裂紋結(jié)構(gòu)力學(xué)響應(yīng)分析的發(fā)展。上個(gè)世紀(jì)末，Dimarogonas 和 Papadopoulos 等人［4－6］在裂紋結(jié)構(gòu)局部柔度的計(jì)算理論方面做出了重要貢獻(xiàn)，其研究成果被廣泛應(yīng)用于土木、機(jī)械等行業(yè)。

局部柔度系數(shù)是裂紋結(jié)構(gòu)振動(dòng)分析、裂紋識(shí)別的基本參數(shù)，目前根據(jù)局部柔度建立的裂紋模型，絕大多數(shù)是基于矩形或圓形的實(shí)體結(jié)構(gòu)得到的，例如矩陣或圓形截面的梁類(lèi)結(jié)構(gòu)、矩形截面的板類(lèi)結(jié)構(gòu)、圓形截面的桿類(lèi)結(jié)構(gòu)等。而針對(duì)空心圓柱體結(jié)構(gòu)的裂紋模型、振動(dòng)分析和裂紋識(shí)別則鮮有文獻(xiàn)報(bào)道［7－9］，Liu 等人［7］建立了貫穿裂紋管的裂紋模型，研究了管道軸向、橫向振動(dòng)的特點(diǎn)，利用裂紋管軸向與橫向耦合振動(dòng)特性進(jìn)行裂紋識(shí)別，文中沒(méi)有考慮剪切力下的局部柔度的作用。Zheng等人［8］分別推導(dǎo)了含橫向裂紋的矩形、圓形截面空心柱體在純彎矩作用下的局部柔度方程，并使用128點(diǎn)高斯積分計(jì)算無(wú)量綱的局部柔度系數(shù)，文中沒(méi)有考慮軸向、剪力的影響。Naniwadekar等人［9］使用靜、動(dòng)力方法確定了含非貫穿直裂紋的管道在純彎矩作用下4種裂紋深度的局部柔度系數(shù)，但文中沒(méi)有使用應(yīng)力強(qiáng)度因子建立裂紋管局部柔度的理論解。

本文根據(jù)線(xiàn)性斷裂力學(xué)理論，推導(dǎo)了非貫穿直裂紋管在軸力、剪力和彎矩聯(lián)合作用下的局部柔度方程，克服了當(dāng)前方法僅針對(duì)特定的荷載模式或非空心截面的缺陷，采用適應(yīng)性的Simpson數(shù)值積分方法求解得到裂紋管的附加柔度系數(shù)，繼而建立了裂紋管結(jié)構(gòu)的有限元模型。實(shí)例分析了裂紋位置、裂紋程度變化對(duì)裂紋管結(jié)構(gòu)自振頻率的影響。

1 裂紋管局部柔度系數(shù)理論推導(dǎo)

假設(shè)管道裂紋為張開(kāi)型裂紋，即在振動(dòng)過(guò)程中假設(shè)結(jié)構(gòu)中裂紋一直處于張開(kāi)狀態(tài)。非貫穿直裂紋是管類(lèi)結(jié)構(gòu)中常見(jiàn)的損傷類(lèi)型之一，如圖1所示。

圖1 (a)裂紋管示意圖;(b)裂紋管單元;(c)裂紋截面幾何尺寸Fig.1 (a)Sketch of pipe with a straight front and part-through crack;(b)Cracked pipe element;(c)Cracked section geometry

非貫穿直裂紋如圖1(a)所示，裂紋深度為a，管壁厚為t，管外徑為De，管內(nèi)徑為Di。裂紋管單元受到軸力P1、剪力P2和彎矩P3的聯(lián)合作用。假設(shè)P1方向與管軸重合;P2和P3關(guān)于裂紋橫截面C－C對(duì)稱(chēng)，合力F方向見(jiàn)圖1(c)。與梁類(lèi)結(jié)構(gòu)裂紋不同，管類(lèi)結(jié)構(gòu)非貫穿裂紋區(qū)域是一個(gè)圓弧形區(qū)域，裂紋深度不再是一個(gè)恒定的常數(shù)，對(duì)于此類(lèi)型裂紋，無(wú)法直接獲得應(yīng)力強(qiáng)度因子求解其局部柔度系數(shù)。本文根據(jù)Dimarogonas［4］建立裂紋轉(zhuǎn)軸局部柔度的思想，把裂紋區(qū)域離散為一序列獨(dú)立的矩形條帶，各矩形條帶按照裂紋梁理論計(jì)算附加應(yīng)變能，然后積分得到總應(yīng)變能，從而求得裂紋引入的局部柔度。

根據(jù)圖1(c)所示的幾何關(guān)系，得到如下的表達(dá)式:

式中:ba表示裂紋深度ξ處水平截面的一半寬度，ξ'為距離積分條帶頂部的局部深度變量，h'(η)為積分條帶深度，ξ、η分別為全局坐標(biāo)下的深度變量和偏移距離。

假設(shè)在外力作用下，結(jié)構(gòu)中裂紋區(qū)域處于彈性階段，根據(jù)線(xiàn)彈性斷裂力學(xué)理論，裂紋出現(xiàn)所產(chǎn)生的附加應(yīng)變能［5］表示為:

式中:J為應(yīng)變能釋放率，Ac為有效裂紋面積。裂紋引起的附加應(yīng)變能釋放率J可表示為:

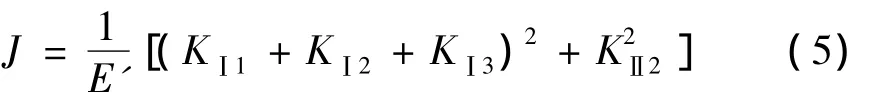
式中:KⅠ1、KⅠ2、KⅠ3分別為軸力、剪力、彎矩引起的Ⅰ型裂紋的應(yīng)力強(qiáng)度因子;為剪力引起的Ⅱ型裂紋的應(yīng)力強(qiáng)度因子。在平面應(yīng)力狀態(tài)下E'=E;在平面應(yīng)變狀態(tài)下E'=E/(1－υ2)。其中，E為彈性模量，υ為泊松比。

對(duì)于裂紋管，在軸力、剪力和彎矩作用下，各條帶裂紋區(qū)域應(yīng)力強(qiáng)度因子可表示為［10］:

式中:Pi(i=1，2，3)分別表示裂紋單元的軸力、剪力和彎矩，γ=Di/De，F(xiàn)1、F2、FⅡ?yàn)閼?yīng)力強(qiáng)度因子的修正系數(shù)，可表示為［11］:

根據(jù)卡式定理(Castigliano’s theorem)，裂紋引入的附加位移可表示為應(yīng)變能對(duì)力的導(dǎo)數(shù):

則裂紋引起的附加局部柔度可表示為:

式中:cij(i，j=1，2，3)為各對(duì)應(yīng)荷載引入的裂紋管附加柔度。

轉(zhuǎn)換積分表示方式，設(shè)x=ξ/De，y=η/De。

由式(2)、式(3)得:

把式(6)～式(9)代入式(14)，進(jìn)行無(wú)量綱處理，得到非貫穿直裂紋管的無(wú)量綱局部柔度系數(shù)PTF。為了區(qū)別于局部柔度系數(shù)cij，下文把無(wú)量綱局部柔度系數(shù) PTF簡(jiǎn)稱(chēng)為“無(wú)量綱柔度”。

式(16)～式(19)是關(guān)于x，y內(nèi)積分限為函數(shù)的雙重積分，且內(nèi)部積分函數(shù)形式復(fù)雜，無(wú)法直接獲得無(wú)量綱柔度的解析解。本文采用適應(yīng)性Simpson數(shù)值積分方法編寫(xiě)程序?qū)ι鲜龇匠踢M(jìn)行求解，適應(yīng)性Simpson算法具有求解速度快，精度高等特性［12］。

2 理論驗(yàn)證

Naniwadekar等人在文獻(xiàn)［9］中使用靜力和動(dòng)力的測(cè)試方法得到了不同裂紋深度非貫穿直裂紋管在純彎矩作用下的扭轉(zhuǎn)彈簧剛度。以文獻(xiàn)［9］中裂紋管道的試驗(yàn)?zāi)Ｐ蜑榛鶞?zhǔn)，根據(jù)本文方程計(jì)算基準(zhǔn)模型局部柔度系數(shù)的理論解，通過(guò)與Naniwadekar等人的試驗(yàn)值對(duì)比驗(yàn)證本文局部柔度系數(shù)推導(dǎo)和求解的合理性。

文獻(xiàn)［9］中靜力測(cè)試裂紋等效剛度Kt表示為:

式中:M為裂紋截面位置的彎矩，ΔU為裂紋引起的附加應(yīng)變能。裂紋管在彎矩作用下局部柔度系數(shù)c33可表示為等效剛度的倒數(shù):

本文推導(dǎo)的局部柔度系數(shù)c33表示為:

基準(zhǔn)模型管的物理參數(shù)和裂紋深度如表1所示，基準(zhǔn)模型管局部柔度系數(shù)c33的計(jì)算值與試驗(yàn)值如圖2所示。

表1 物理參數(shù)和裂紋深度Tab.1 Physical parameters and crack depth

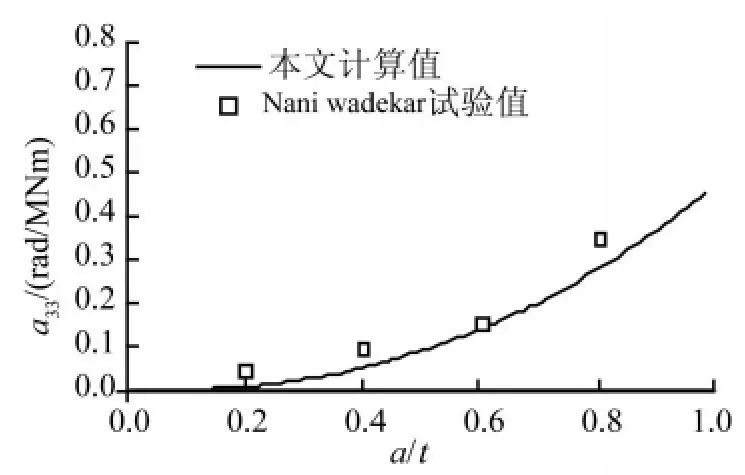
圖2 基準(zhǔn)模型局部柔度系數(shù)的計(jì)算值與試驗(yàn)值Fig.2 Calculating results and experimental results of the local flexibility due to a crack

從圖2中可以看出:隨著裂紋深度的增加，裂紋管局部柔度系數(shù)的理論解與試驗(yàn)值都逐漸增大。使用本文理論求解的局部柔度系數(shù)與試驗(yàn)測(cè)試結(jié)果基本吻合，本文的理論解略低于試驗(yàn)值。相對(duì)于文獻(xiàn)［9］，本文給出了非貫穿直裂紋管在軸力、剪力和彎矩作用下局部柔度系數(shù)的理論推導(dǎo)和求解方法，使用該方法可以求解任意裂紋深度非貫穿直裂紋管的各局部柔度系數(shù)，避免為了獲得局部柔度系數(shù)進(jìn)行的大量試驗(yàn)工作，且求解結(jié)果滿(mǎn)足工程實(shí)際要求。

3 裂紋管有限元模型

求得裂紋管局部柔度系數(shù)后，可建立使用扭轉(zhuǎn)彈簧模擬的“彈簧鉸”裂紋模型或使用局部柔度矩陣構(gòu)建的“有限元”裂紋模型。如圖1(a)所示裂紋管單元的總體柔度等價(jià)于無(wú)裂紋單元柔度與裂紋引起局部柔度的代數(shù)和［10］

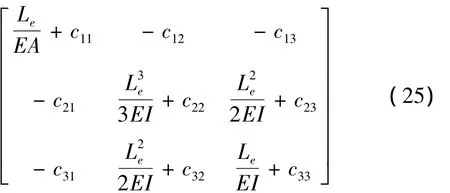
式(25)可進(jìn)一步表示為含裂紋單元的剛度形式:

其中，轉(zhuǎn)換矩陣T表示為:

裂紋管道的動(dòng)力特征方程表示為:

式中:K、D、M分別為裂紋管道的總剛度矩陣、阻尼矩陣和質(zhì)量矩陣;ωn、Φn分別為固有圓頻率和振型。

假設(shè)裂紋不引起結(jié)構(gòu)質(zhì)量矩陣的變化，則無(wú)裂紋管單元?jiǎng)偠染仃嚭凸軉卧恢沦|(zhì)量矩陣分別表示為:

根據(jù)上述裂紋管有限元模型，可以計(jì)算任意裂紋位置、裂紋深度管類(lèi)結(jié)構(gòu)的固有頻率和振型。

4 實(shí)例分析

應(yīng)用建立的含非貫穿直裂紋管道的有限元模型，分析裂紋管結(jié)構(gòu)的振動(dòng)特性，實(shí)例模型如圖3所示。管道長(zhǎng)度 L為 1.0 m，內(nèi)徑 Di為 0.02 m，外徑 De為0.04 m，密度ρ為7850 kg/m3，彈性模型 E 為206 GPa，泊松比 υ為0.27。

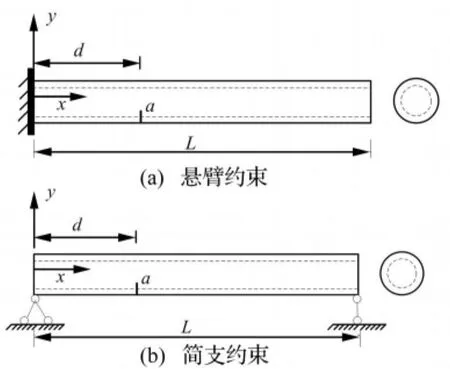
圖3 裂紋管類(lèi)結(jié)構(gòu)示意圖Fig.3 Sketch of the cracked pipe-like structure

為了直觀描述變化規(guī)律定義無(wú)量綱參數(shù)，即固有頻率變化率Fr，表達(dá)式如下:

圖4和圖5分別給出了懸臂約束、簡(jiǎn)支約束兩種條件下含非貫穿直裂紋管道的前三階固有頻率隨裂紋位置、深度的變化率Fr，圖中x/L、a/t分別為裂紋相對(duì)位置和相對(duì)深度。

圖4 裂紋管道的前3階固有頻率變化(懸臂約束)Fig.4 .Variations of the natural frequencies of the cracked pipe for the first three modes(cantilever constraint)

圖5 裂紋管道的前3階固有頻率變化(簡(jiǎn)支約束)Fig.5 Variations of the natural frequencies of the cracked pipe for the first three modes(simple support constraint)

從圖4和圖5中可以看出:

(1)無(wú)論對(duì)于懸臂約束，還是簡(jiǎn)支約束，在裂紋位置相同條件下裂紋越深，其Fr值越大，固有頻率降低越明顯。

(2)在裂紋深度相同條件下，不同裂紋位置、不同邊界約束條件以及不同階次固有頻率的Fr值也是不相同的。懸臂約束條件下，結(jié)構(gòu)一階固有頻率呈現(xiàn)單調(diào)變化，裂紋距離固定端越近，裂紋越深Fr值越大，反之越小。簡(jiǎn)支約束條件下，F(xiàn)r值分布關(guān)于x=0.5L對(duì)稱(chēng)。懸臂或簡(jiǎn)支約束條件下，結(jié)構(gòu)二階、三階固有頻率的Fr值并不隨著裂紋位置的改變呈單調(diào)性變化，當(dāng)裂紋越接近模態(tài)振型振幅為0的節(jié)點(diǎn)，結(jié)構(gòu)固有頻率變化越小;當(dāng)裂紋越接近模態(tài)振型局部最大振幅的節(jié)點(diǎn)，結(jié)構(gòu)固有頻率變化越明顯。

5 結(jié)論和展望

本文從斷裂力學(xué)基本理論出發(fā)，推導(dǎo)了含非貫穿直裂紋管道在復(fù)雜聯(lián)合荷載作用下的局部柔度系數(shù)，通過(guò)與Naniwadekar等人模型試驗(yàn)結(jié)果比較驗(yàn)證了本文局部柔度系數(shù)計(jì)算結(jié)果的合理性，為裂紋管的結(jié)構(gòu)分析和裂紋識(shí)別提供了理論基礎(chǔ)，克服了當(dāng)前方法僅能針對(duì)特定的荷載模式或非空心截面的缺陷。

本文將管道視為梁－桿模型，避免了建立三維殼模型進(jìn)行理論分析的難度，同時(shí)又有較高的精確度，可以滿(mǎn)足工程需要。

根據(jù)建立的裂紋管有限元模型，研究了裂紋位置、裂紋深度與結(jié)構(gòu)固有頻率之間的關(guān)系。結(jié)果表明，當(dāng)裂紋位于或接近模態(tài)振型振幅為0的節(jié)點(diǎn)時(shí)，裂紋對(duì)結(jié)構(gòu)固有頻率影響較小，而當(dāng)裂紋位于或接近模態(tài)振型局部最大振幅的節(jié)點(diǎn)時(shí)，裂紋對(duì)結(jié)構(gòu)固有頻率影響顯著。

本文研究了非貫穿直裂紋管局部柔度系數(shù)的求解方法以及固有振動(dòng)特性，有關(guān)其它裂紋形式管的局部柔度系數(shù)求解方法和振動(dòng)特性分析作者將另外討論。

［1］Dimarogonas A D.Vibration of cracked structure:a state of the art review［J］.Engineering Fracture Mechanics，1996，55(5):831－857.

［2］胡家順，馮 新，李 昕，等.裂紋梁振動(dòng)分析和裂紋識(shí)別方法研究進(jìn)展［J］.振動(dòng)與沖擊，2007，26(11):146－152.

［3］Irwin G R.Analysis of stresses and strains near the end of a crack traversing a plate［J］.Journal of Applied Mechanics.1957，24:361－364.

［4］Dimarogonas A D.Analytical methods in rotor dynamics［M］.Applied Science Publishers，Essex，1983.

［5］Papadopoulos C A.The strain energy release approach for modeling cracks in rotors:A state of the art review［J］.Mechanical Systems and Signal Processing，2008，22(4):763－789.

［6］Papadopoulos C A.Some comments on the calculation of the local flexibility of cracked shafts［J］.Journal of Sound and Vibration 2004，278(4－5):1205－1211.

［7］Liu D，Gurgenci H，Veidt M.Crack detection in hollow section structures through the coupled response measurements［J］.2003，261(1)17 －29.

［8］Zheng D Y，F(xiàn)an S.Vibration and stability of cracked hollowsectional beams［J］.Journal of Sound and Vibration，2003，267(4):933－954.

［9］Naniwadekar M R，Naik S S，Maiti S K.On predection of crack in different orientations in pipe using frequency based approach［J］.Mechanical Systems and Signal Processing，2008，22(3):693－708.

［10］Zheng D Y，Kessissoglou N J.Free vibration analysis of a cracked beam by finite element method［J］.Journal of Sound and Vibration，2004，273(3):457－475.

［11］Tada H，Paris P C，Irwin G R.The stress analysis of cracks handbook(ThirdEdition) ［M］.NewYork:ASME Press，2000.

［12］Gander W，Gautschi W.Adaptive Quadrature-Revisited［J］.BIT，2000，40:84－101.

［13］Nikolakopoulos P G，Katsareas D E，Papadopoulos C A.Crack identification in frame structures［J］.Computers and Structures，1997，64(1－4):389－406.