磁選態銫鐘內輻射頻移及其對準確度的影響

黃良育，張滌新，陳 江，王 驥

（蘭州物理研究所，甘肅 蘭州 730000）

1 引言

磁選態銫原子頻標由于具有好的可靠性和長期穩定性等特點，已在時頻系統、導航定位和通信等方面得到了廣泛應用。

在1967年第十三屆國際計量大會上對原子秒作了定義，即“秒是銫133原子基態的2個超精細能級之間躍遷所對應輻射的9 192 631 770個周期所持續的時間”[1]。對于銫原子基態6s，核外電子角動量J=1/2，核自旋角動量I=7/2，原子總角動量F=4和3。在外加弱磁場中，原來以F為標志的超精細能級分裂成（2F+1）個以mF為標志的塞曼子能級（即分裂為16個塞曼子能級）。在銫原子頻標中，用于躍遷的2個超精細能級是（F=3，mF=0）和（F=4，mF=0），其躍遷頻率為9 192 631 770 Hz。磁選態銫原子鐘是被動型原子鐘，選出一個子能級躍遷到另一子能級，形成鑒頻信號，利用鎖頻環路去鎖定一個晶體振蕩器產生固定的頻率信號。

磁選態銫原子鐘由2部分組成[2]：（1）物理部分即銫束管，用于產生原子能級躍遷；（2）頻標電路用于產生標準頻率并對頻率進行變換和調整。單束磁選態銫束管工作原理如圖1所示，由銫源、A磁鐵、Ramsey微波腔、B磁鐵和檢測器等零部件組成，產生Ramsey躍遷信號。

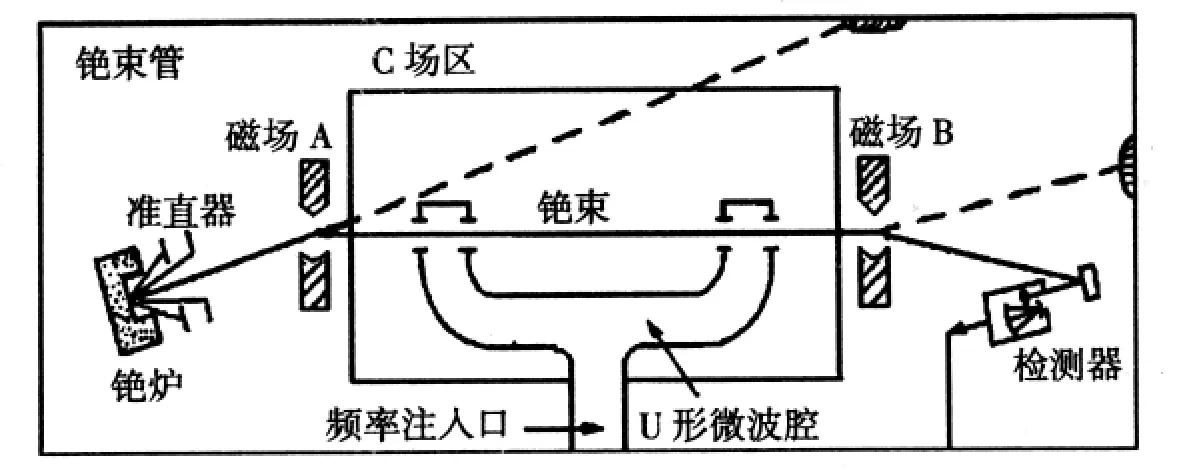
圖1 磁選態銫束管工作原理

加熱裝有高純度銫[3]的銫爐到一定溫度，銫原子通過細長的準直管沿一定方向噴出形成原子束。從銫爐中噴出的銫原子由于處于不同狀態，具有不同磁矩，在通過不均勻磁場A時將因受不同的橫向偏轉力作用而偏向不同方向，從而將F=3的銫原子選出，被選出的銫原子經過較弱的恒定磁場（C場）和微波諧振腔，在頻率為9.192 GHz的微波作用下發生躍遷，躍遷到F=4，mF=0態，躍遷后的銫原子被磁鐵B的偏轉磁場選中進入檢測器中獲得Ramsey躍遷信號。

銫束管的輸出頻率經過選態、C場作用、輻射躍遷、檢測、伺服放大等多個物理和技術處理后的原子躍遷頻率，每一處理步驟都可能使輸出頻率偏離理論值。各種頻移誤差的總和代表輸出頻率偏離定義值的不確定程度，也就是它的準確度[4]。

作者將在輻射場理論的基礎上，詳細討論磁選態銫原子頻標中附加輻射場引起的銫原子基態超精細躍遷頻率的移動，即輻射頻移及其對頻標準確度的影響。

2 磁選態銫鐘內的輻射頻移及影響

根據輻射場與原子相互作用的量子理論[5～7]，如果原子的共振躍遷由某一頻率的輻射場引起，那么任何其他非共振頻率輻射場的存在都會作為干擾改變躍遷頻率。這種干擾是通過電磁場與原子電偶極矩或磁偶極矩的相互作用，即交流Stark效應和交流Zeeman效應使原子能級發生變化，從而導致原子躍遷頻率的移動。

考慮二能級原子系統與頻率為ω的輻射場相互作用，根據量子力學的微擾理論，當遠大于躍遷線寬時，可計算出由頻率為ω的輻射場引起原子躍遷頻率的移動為

式中 ω0為原子固有頻率，即原子未受干擾時的躍遷頻率；場強參量b表示輻射場與原子相互作用的大小，與電磁場強度及聯系兩能級的偶極躍遷矩陣元成正比，對于電偶極相互作用

式中 pz為原子電偶極矩算符在電場方向的分量；ψm，ψn為原子上下能級波函數。對于磁偶極相互作用

式中 B0為輻射場磁場分量振幅；磁偶極躍遷矩陣元μmn為

式中 μz為原子磁偶極矩算符在磁場方向的分量。

由式（1）、（2）和式（4）可見，輻射頻移與場強平方，即與功率成正比，因此輻射場功率越大，則輻射頻移越大。通常在頻標相互作用區內因各種原因不可避免地存在著一些附加輻射場，這些輻射場將會通過交流Stark效應或交流Zeeman效應使原子基態兩超精細能級移動，從而使超精細躍遷頻率移動，造成輻射頻移。

2.1 Bloch-Siegert效應

133Cs原子基態超精細躍遷為磁偶極躍遷，要求激勵微波場為圓偏振場。由于所需要的圓偏振場不易產55生，實際中通常用線偏振場激勵共振。由于線偏振場可以分解為偏振方向相反的2個圓偏振場，用線偏振場代替圓偏振場相當于增加了一反向的圓偏振場，它將使共振能級產生微小移位，從而導致原子共振頻率移動，亦即Bloch-Siegert效應。

對Ramsey共振，其相對頻移為

式中 P0為與最佳b0值相應的最佳微波功率。k（P）由下式給出

2.2 微波頻譜不純及調制影響

由于受電源紋波等寄生調制的影響，激勵原子躍遷的微波輻射頻譜常由主頻及若干邊帶所組成，這些邊帶相當于附加輻射場，會引起標準譜線頻移。

設主頻與旁頻頻率分別為ω0、ωi，它們的場強參量分別用b及bi表示，邊帶功率Pi∝b2i，旁頻與主頻的功率比為Ai=Pi/P，則相對頻移為

式中 P0為最佳載頻功率；Δνi為旁頻與主頻的頻差Δνi=νi-ν，邊帶離主頻愈近，功率愈大，引起的頻移也愈大。由此可知，對稱邊帶不產生頻移，調制不善所產生的非對稱邊帶將會引起頻移。

為估計此項頻移，需要精確測量實際微波頻譜結構，主要是邊帶相對強度Ai和不對稱度Δpi/pi。微波頻譜的結構是由微波激勵電路決定，為了避免或減少由微波頻譜不純引起的頻移，在微波激勵電路的設計和制作中，應設法抑制頻譜中的邊帶，改善頻譜純度，盡可能避免不對稱邊帶的存在。這是頻標電路設計和制作的一個重要原則和基本要求。就目前的制作水平，一級邊帶相對強度小于10-5，引起的相對頻移小于10-13數量級。

2.3 Stark效應與黑體輻射

銫原子基態為S態，沒有一級Stark效應，但存在交流Stark效應，微波輻射場的電振動會使能級有微小影響。由于超精細能級之間沒有電偶極矩耦合，所以這種影響通過基態與激發態之間的電偶極相互作用反映出來，而它們之間的能量差與微波光子能量相差很遠，所以頻移較小約為1×10-15。

電磁波與原子相互作用中一個最常見的現象就是吸收和色散，實際上吸收和色散都是指原子對波的作用而言。電磁波對原子的作用可以分為波對原子內部運動（電子相對于核運動）和外部運動（原子質心運動）的作用，對原子內部運動作用，吸收對應于原子內部能級間躍遷，色散對應于原子能級的移動（即交流Stark和Zeeman效應）。微波諧振腔內的熱輻射場通過交流Stark和Zeeman效應使基態超精細能級發生微小移動。由于熱輻射場頻譜分布不對稱，故2個超精細能級的移動不一致。交流Zeeman效應引起的（0—0）線頻移小于1×10-16數量級，相對于目前磁選態銫原子頻標要求的準確度±1×10-12，其影響可以忽略不計。

二級Stark效應引起的頻移為

對上式微分得

在室溫T=300 K附近，這一項的修正值為-1.7×10-14，溫度變化1 K，帶來誤差-2.3×10-16。在實際應用中溫度波動小于10 K，這一項引起的頻移小于10-15。

2.4 Majorana躍遷的影響

銫束管中原子在選態磁場和C場中運動，原子感受到磁場大小和方向都會有所變化。由于原子磁矩是以磁場方向為量子化軸，當磁場變化時，原子量子化狀態可能來不及跟隨磁場變化，從而產生非緩變的能級躍遷，即Majorana躍遷。在銫束管中，Majorana躍遷主要發生在從強選態磁場到C場之間的過渡區及C場屏蔽附近；若C場不均勻，有橫向場分量，原子在運動中會感受到符合塞曼躍遷頻率磁場變化的傅立葉成分，也會引起這種躍遷。如果C場方向與選態磁場方向不同或相反時，這種躍遷的可能性很大。

Majorana躍遷的頻移機制比較復雜，理論估算和實驗測試Majorana頻移都非常困難。因此，Majorana躍遷已經成為限制銫束管頻率準確度的一個重要的誤差來源。Majorana躍遷的主要后果是：1）降低了信噪比，從而損害頻標的短期穩定度；2）改變了銫原子的運行軌道，因此改變了與此有關的頻移；3）改變了原子的速率分布，與原子速率分布相關的頻移同時發生變化，如二階多普勒頻移、鄰近躍遷引起的頻移等。

在相同的設計下，工藝、加工與安裝調整的好壞，對Majorana躍遷大小影響很大。為了避免Majorana躍遷的產生，實際中采用如下措施：1）保證在選態磁場與C場之間不產生橫向磁場分量；2）使場強過渡比較平滑，可以給選態磁鐵加屏蔽或者在過渡區安裝磁場引導裝置；3）保證A、B磁場與C場嚴格平行，以避免在銫原子束通過過渡區時引起橫向場，比如可適當擴大C場與A、B磁鐵的間距；4）C場盡可能均勻。

3 結論

通過分析磁選態銫原子頻標中輻射場引起頻移的原因，計算了各種形式輻射頻移的大小，討論它們對頻標準確度的影響，其中Majorana躍遷對頻標準確度的影響最大，給出了減小該躍遷以提高頻標準確度的方法，對于進一步提高磁選態銫原子頻標的性能有重要的指導意義。

[1]《計量測試技術手冊》編輯委員會．計量測試技術手冊·第11卷·時間頻率[M]．北京：中國計量出版社，1996.

[2]JACQUES VANIER，CLAUDE AUDOIN.The quantum physics of atomic frequency standards volume 1[M].USA:IOP publishing Ltd，1989.

[3]馬寅光，張滌新，劉蘇明.金屬銫真空蒸餾提純裝置的研制[J].真空與低溫，2008，14（2）:99～102.

[4]王義遒，王慶吉，傅濟時，等.量子頻標原理[M].北京：科學出版社，1986.

[5]SALWEN H.Resonance transitions in molecular beam experiments.I.general theory of transitions in a rotating magnetic field[J].Phys.Rev.，1955，99（4）:1274～1286.

[6]NORMAN，F.RAMSEY.Resonance transitions induced by perturbations at two or more different frequencies[J].Phys，Rev，1955，100（4）:1191～1194.

[7]MIZUSHIMA M.Theory of resonance frequency shift due to radiation field[J].Phys，Rev，1964，133（2A）:A414～A418.