一種高精度GPS基線網抗差估計方法

王 彬,高井祥,王 堅,鄭南山

(1.中國礦業大學環境與測繪學院,江蘇徐州221116;2.國土環境與災害監測國家測繪局重點實驗室,江蘇徐州221116;3.江蘇省資源環境信息工程重點實驗室,江蘇徐州221116)

0 引 言

隨著現代科研和工程項目對GPS定位精度要求的不斷提高,許多情況下要建立高精度的GPS控制網,數據處理時,一般采用Gamit、Bernese等精密基線解算軟件進行解算,然后將帶有協方差陣的基線作為觀測值進行整網的平差。GPS觀測量受衛星數據質量和周圍環境的影響較大,野外檢核條件也較少,所以,GPS觀測量中經常包含有粗差,雖然經過精密的基線解算,已經剔除了大部分的粗差,但是有時仍會殘留一小部分粗差,這將嚴重損害GPS定位的精度,如何處理這些粗差是提高定位精度的關鍵。

GPS基線向量網的平差處理,通常取各觀測時段獨立基線作為觀測量,可以解決基線向量之間幾何相關的問題。而同一時段幾何獨立的基線向量之間仍是隨機相關的[1],國內多種平差軟件為了簡化計算,也都忽略了這種相關性,對于一般工程應用仍能滿足要求,但是對于高精度的GPS網平差,則應考慮這種相關性,使數學模型上更嚴密。

由于基線向量之間存在較強的相關性,使得粗差的處理變得更加復雜,我們需要引入相關抗差估計的方法。相關觀測的抗差估計,已有一些較為成功的方法,如相關分析的方法[2]、基于標準化殘差法[3]、以及RECO方案及其改進[4]等。這些方法有各自的優缺點,有的對于相關觀測抗差性不強,效果并不明顯,有的選取的單位權方差不合適時將直接影響抗差效果,有的降權的效率很高但不夠平穩,可能會導致迭代的不收斂。主要介紹一種標準化殘差構造的抗差模型,利用中位數計算單位權方差因子,根據具體情況對IGG3的權因子函數進行改進,通過實測GPS基線網的算例,說明了該方法的可靠性與實用性。

1 GPS基線網相關抗差估計方案

設有線性模型

ε為相關觀測隨機誤差向量,且E(ε)=0,先驗權陣為p,誤差方程為

一般,權因子γi采用IGG3函數計算。有時,為使降權更加平穩,將IGG3降權段的平方去掉,得到的權因子函數為

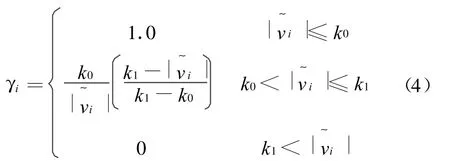
式中:vi為第i個觀測值殘差;qvi是vi的權倒數;σ0是由中位數計算的單位權方差因子,其計算公式可取為[5]

式中,MEDIAN是中位數的計算函數。

k0和k1為閾值,實際計算中,k0通常取3.0～5.0,k1通常取8.0～10.0。

抗差估計需要迭代,其迭代計算公式為

式中,k>1,k=1是進行最小二乘估計,權倒數qv在迭代過程中保持不變,當參數的兩次估值之差絕對值的最大值小于迭代精度時,停止迭代,此時就可得參數估值的抗差解。

單位權中誤差計算公式為

n0是權因子等于0的觀測值個數,即被淘汰的觀測分量數。

這樣構造的抗差模型具有以下特點:

1)由中位數計算的單位權方差因子與標準化殘差結合具有更好的抗差性,而且可以克服由于σ0取值不當而影響抗差效果的不足;

3)根據實際情況,當降權過快導致迭代不收斂時,使用對IGG3改進的權因子函數可使降權更加平穩;

2 GPS基線網平差驗后單位權方差的檢驗

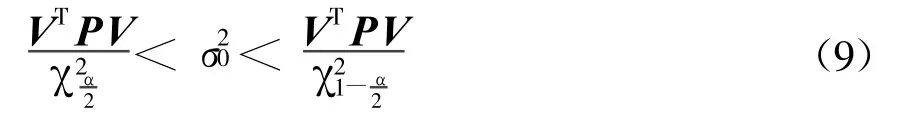
則接受H0假設,檢驗通過;反之,則拒絕H0,接受 H1,未通過檢驗,認為觀測值中含有粗差或驗前權選取不合適。

在GPS網的最小二乘平差完成后,進行χ2分布檢驗,若未通過檢驗,則需進行抗差估計,計算完成后還需進行χ2分布檢驗,若還未通過檢驗,則說明驗前權陣選取不合適,需要通過整網的赫爾默特方差分量估計[7]進行調整。

3 算例分析

基于C#語言,編寫了高精度GPS網平差與抗差估計程序,用于驗證抗差模型的可靠性與實用性,程序能夠實現數據文件的讀取、最小二乘平差、抗差估計、結果文件輸出等主要的功能。

某一實測GPS控制網如圖1所示,網中共有6個點,其中JZ01、JZ02為已知點,共觀測了6個時段,各個時段幾何獨立的基線向量個數分別為:3,3,3,3,3,2,即共有17條基線向量觀測值參與平差。

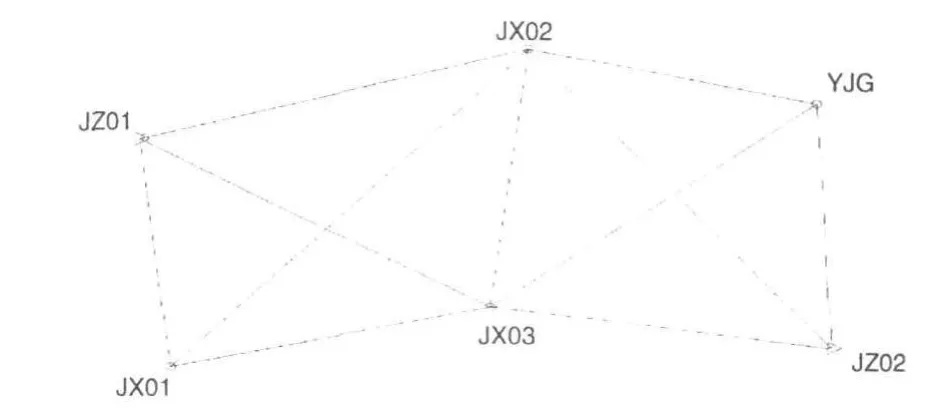
圖1 GPS基線網

計算數據采用該網的基線解算文件,已通過了基線重復性和獨立閉合環檢驗,直接提取基線觀測量和協方差陣。

3.1 方案設計

方案0:取先驗單位權中誤差σ0=1。經過LS估計所得驗后單位權方差為^σ0=1.14,通過 χ2分布檢驗,認為觀測值中無粗差,再進行抗差估計,與最小二乘結果完全相同;

方案1:在第一時段JZ02-YJG的dx觀測分量上加入-0.1 m的粗差;

方案2:在第二時段Jx02-Jx03的dz觀測分量上加入0.2 m的粗差;

方案3:方案1的基礎上,在第二時段Jx02-YJG的dx觀測分量上加入0.01 m;

方案4:在方案2的基礎上,在第五時段YJGJx02的dz觀測分量上加入-0.3 m的粗差;

方案5:在方案4的基礎上,在第三時段Jx01-Jx02的dx觀測分量上加入0.08 m的粗差;

方案6:分別在第六時段JZ01-Jx02各個觀測分量上加上-0.2 m,0.3 m,0.2 m的粗差

對方案1～6進行分別進行LS估計和抗差估計,抗差估計中k0取3.0,k1取8.0,迭代收斂條件eps=0.0001 m.

3.2 平差結果比較

從表1可以看出:當觀測值中不含粗差時,最小二乘估計與抗差估計結果相同,方案1～6中使用不同的加粗差方案時,無論是單位權中誤差還是點位誤差都明顯增大,無法通過檢驗,而經過抗差估計后,均可通過檢驗,且與不含粗差時最小二乘估計結果相差很小。

分別取先驗單位權中誤差 σ0=0.01,0.1,0.2,表中后驗單位權中誤差變為相應的倍數,均可通過χ2分布檢驗,其它結果不變。

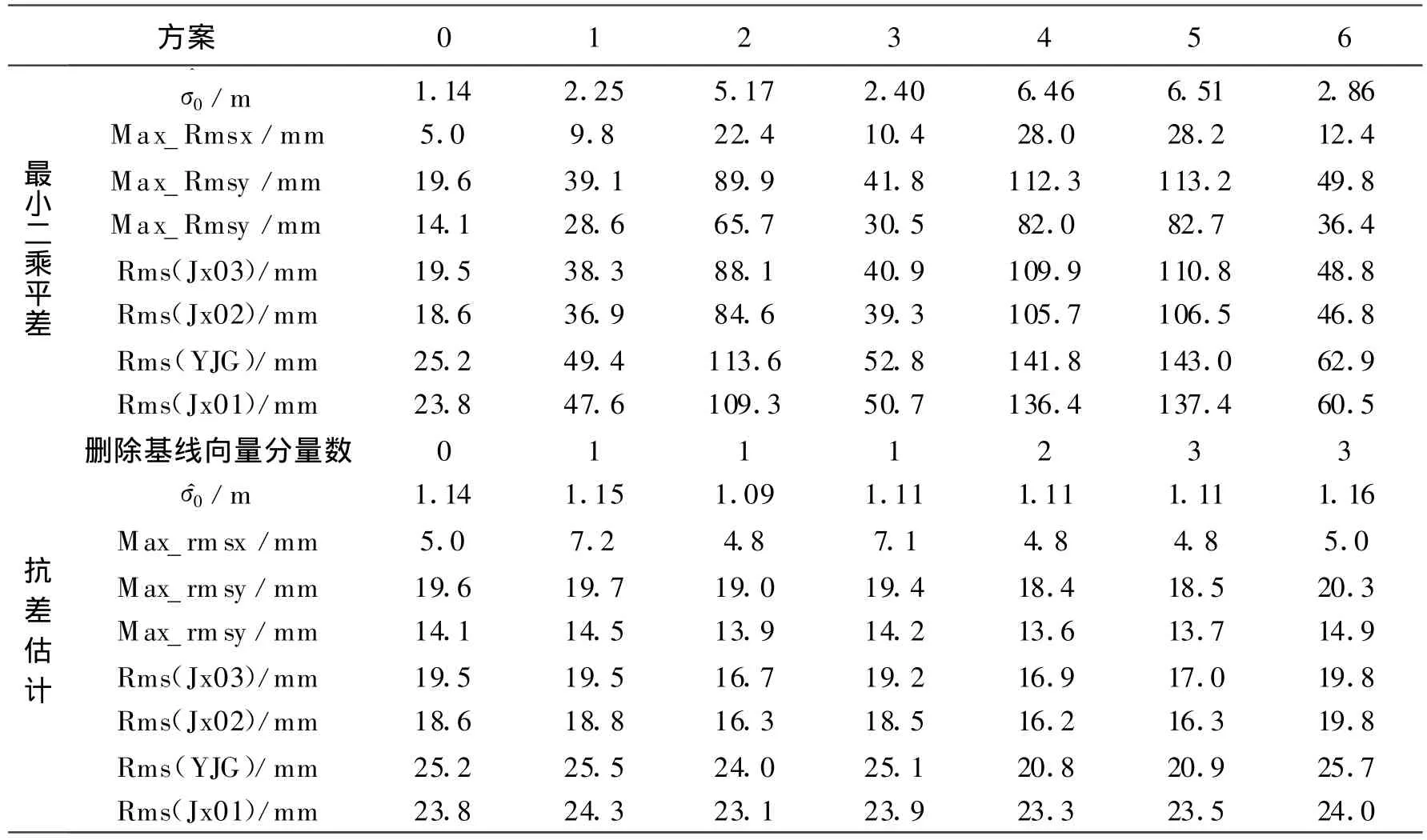
表1 抗差估計與最小二乘結果比較表

3.3 粗差識別

對比表1和方案1～6可看出:等價權因子γi=0的觀測分量,都是所加粗差的分量;γi=0的觀測值之殘差,且與所加粗差的符號相反,絕對值大致相同。需要說明的是,方案3中,雖在第二時段Jx02-YJG的dx觀測分量上加入了0.01 m的粗差,但由于數值較小,對觀測值精度影響很小,只是懷疑有粗差而被降權,并沒有完全剔除,這樣也相當于保留了部分真實的觀測信息。總的來說,該抗差模型對粗差的識別與處理是較為準確可靠的。

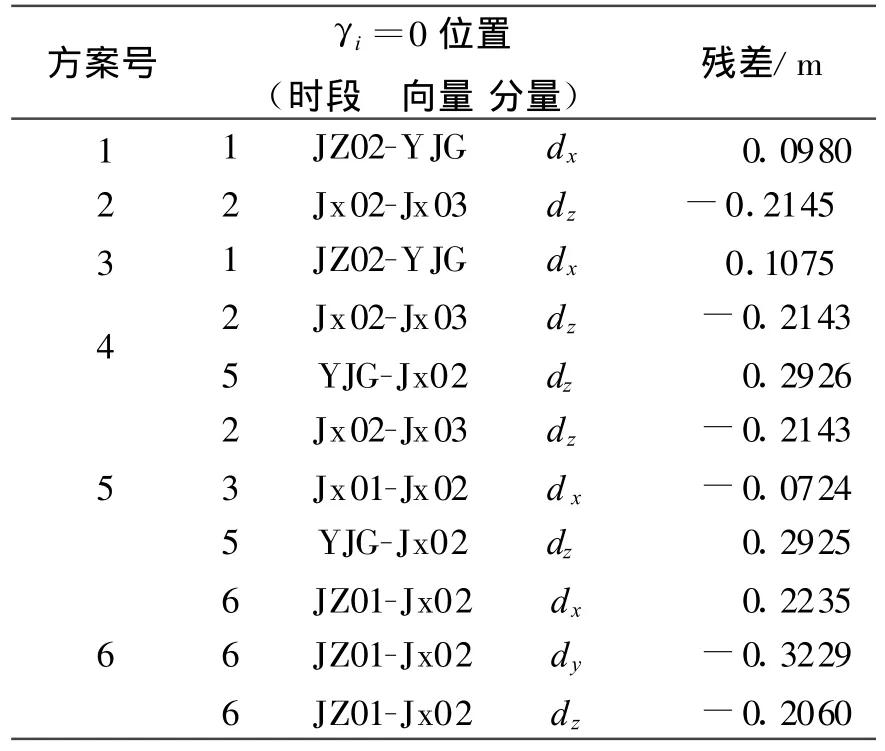
表2 粗差識別

3 結 論

1)由于標準化殘差和中位數本身都具有一定的抗差性,將它們結合在一起能夠有效消除或減弱觀測粗差對平差成果的影響,而且克服了一些抗差模型中先驗單位權中誤差σ0取值不當影響抗差效果的缺陷,適合于高精度的GPS基線網平差;

2)針對實際情況,對IGG3權因子函數的改進,使降權不僅有效而且平穩;

3)當網中不含粗差時,該抗差模型與最小二乘平差所得結果一致,當網中含有粗差時,該抗差模型對粗差的位置和大小可以做出較為準確的識別和估計,與傳統粗差探測方法相比具有較大的優勢,將更有利于GPS數據后處理的自動化。

[1] 黃觀文.GPS精密單點定位和高精度GPS基線網平差研究與軟件實現[D].西安:長安大學,2009.

[2] 陶本藻,姚宜斌,施 闖.基于相關分析的粗差可區分性[J].武漢大學學報?信息科學版,2004,29(10):881-883.

[3] 余學祥,呂偉才.基于標準化殘差的相關觀測抗差估計模型[J].武漢測繪科技大學學報,1999,24(1):75-78.

[4] 趙慶海.高精度GPS向量網抗差估計[J].測繪學報,2004,33(1)43-46.

[5] 宋力杰.測量平差程序設計[M].北京:國防工業出版社,2009.

[6] 李征航,黃勁松.GPS測量與數據處理[M].武漢:武漢大學出版社,2005.

[7] 崔希璋,於宗儔,陶本藻,等.廣義測量平差[M].2版,武漢:武漢大學出版社,2009.