線性規劃中幾種內點算法的比較

福州工業學校 林育山

?

線性規劃中幾種內點算法的比較

福州工業學校 林育山

該文是關于內點算法的一篇綜述，對幾種較為實用的求解線性規劃問題的算法進行總結，包括單純形法、橢球算法、Karmarkar算法、原仿射尺度算法等，并對這些算法進行比較。

線性規劃 內點算法 比較

1 問題的提出

1947年，美國數學家G.B . Dantzig提出了求解線性規劃問題的通用方法——單純形法，大量的實際應用表明，單純形法是一種行之有效的解線性規劃問題的算法。但是在理論上，單純形法并不是一個“好算法”，特別是在1972年美國學者V.Klee與G.L.Minty發表了一個例子，通過構造一個病態的線性規劃，說明了單純形法在解決某些極端的例子中效果不好，很多研究線性規劃的數學家開始探討解線性規劃的NP問題。1979年，前蘇聯數學家哈奇揚發表了橢球算法，并證明了該算法是個多項式時間算法，說明線性規劃的多項式時間算法是存在的，但在實際應用中，這一算法并沒有很強的實用性。1984年，在美國貝爾實驗室工作的印度籍數學家N.Karmarkar提出了解線性規劃的投影尺度法，這也是一個多項式時間算法，它比橢球法優化了很多，這一工作一時引起了很多數學家對內點算法的研究熱情，在不斷的改進中，一些新的、改進的或變形的內點算法相繼出現。無論是內點算法還是橢球算法，它們有一個共同點，就是采用了非線性規劃的一些思想來解決線性規劃問題。

2 幾種算法的簡單介紹

2.1 單純形法

將線性規劃問題（LP）寫成如下的矩陣形式：

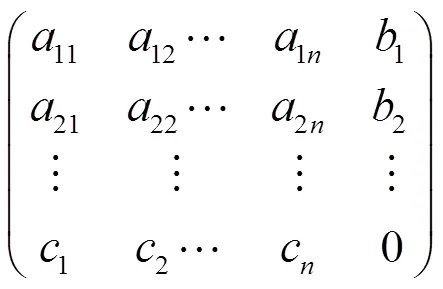
設是的一個基，不失一般性的，設它由中的前列所組成，由高等代數的知識，必可將矩陣（1）通過初等變換變為如下形式：

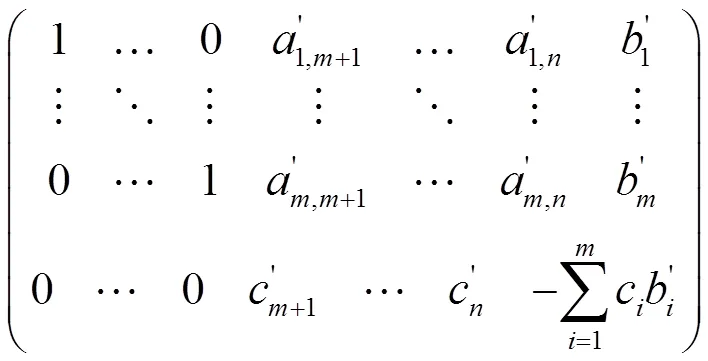
（3）式可以寫成矩陣的形式如下：

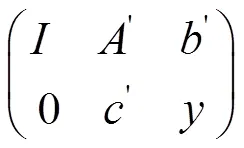
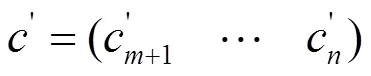
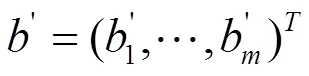
注：

單純形法的具體步驟如下：

Step1 列出初始表，在表中找到一個初始基，化為標準形，得到對應初始基的基本可行解。

Step2 檢查標準形表上的檢驗數(c=m+1, 是否均為正數，若是，則停止，當前的基本可行解為最優解，否則，進入Step 3。

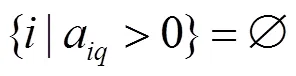
在前面單純形法的介紹中，我們強調了一個非退化的前提，在退化的情況下，用上面的步驟去迭代時，可能出現死循環，對于這個問題，先后有Charnes提出了攝動法，Dantzig、Orden、Wolfe提出了字典序法以及Bland提出了Bland法則，本論文中我們僅介紹Bland法則。

2.2 橢球算法

如果能夠找到求解嚴格不等式組多項式時間算法，那么就有（LP）問題的多項式時間算法。橢球算法就是一種通過尋求嚴格不等式組的多項式時間算法，來證明線性規劃問題有多項式時間算法。可以理解為把線性規劃問題轉化為（8）的形式，即為弱不等式組，然后求出相應的嚴格不等式組的解，從而導出弱不等式組的解，則可以求出原線性規劃問題的最優解。所以橢球算法的本質是求嚴格不等式組的解。下面簡單介紹一下橢球算法的原理。

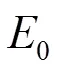
2.2.1基本定義

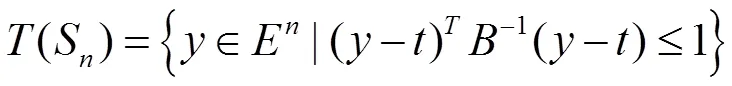
2.2.2橢球算法

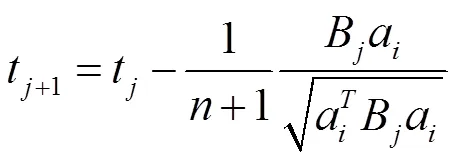
2.3 Karmarkar算法

Karmarkar算法運用了求解非線性規劃問題的思想來解決線性規劃問題。這種算法是在把一般線性規劃問題轉化為Karmarkar所特有的標準型，再利用一種求解這種標準型的算法最終求出最優解。Karmarkar算法把線性規劃問題轉化成它所要求的那種標準型，我們稱之為Karmarkar標準型，形式如下：

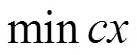
其中這個標準型還要求滿足以下三個條件：

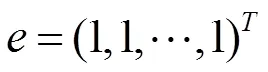
Karmarkar算法的具體步驟：

下面對Karmarkar算法從一個迭代點尋求下一個迭代點的原理進行解釋。

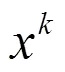
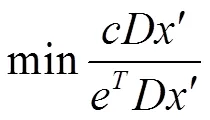
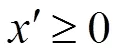
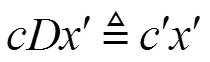
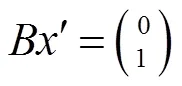
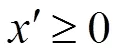
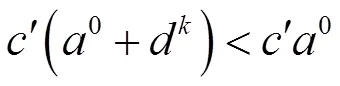
注:

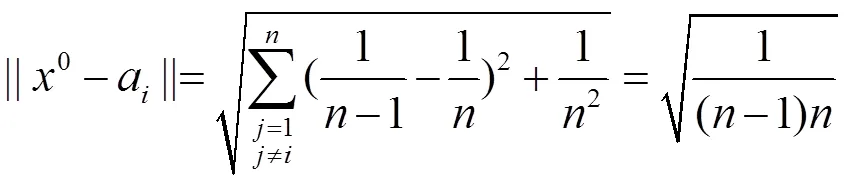
2.4 原仿射尺度算法

原仿射問題與上面介紹的兩種內點算法不同，它是可以求解標準形式的線性規劃問題LP：

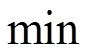
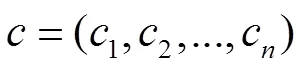
不失一般性的，設秩()=，并設

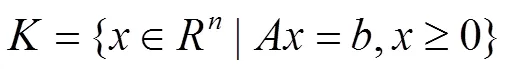
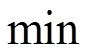
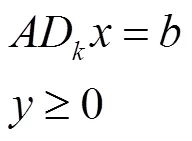
原仿射尺度算法與Karmarkar算法在構造原理上有很多的相似之處，它的好處是不用把一般的線性規劃問題轉化為Karmarkar標準型，由于把一般的問題轉化為Karmarkar標準型并不容易，所以原仿射尺度算法在實際應用中是很受推崇的。但是原仿射尺度算法在理論上并未被證明是一個多項式時間算法。

3 幾種算法的比較

名稱解決的問題解決原理算法的時間應用價值和優缺點 單純形法直接解決線性規劃問題 s.t 在基本可行解中尋找最優基本可行解指數形時間算法大量的實際應用證明單純形法是一種行之有效的解線性規劃問題的算法，但對于一些極端的問題，單純形法效果不好 橢球算法把解決線性規劃問題轉化為求解嚴格不等式組通過不斷縮小嚴格不等式組的解所在的橢球的體積，最終確定是否有解多項式時間算法橢球算法證明了求解線性規劃問題的多項式時間算法的存在，但在實際應用中，遠沒有單純形法好用 Karmarkar算法把解決線性規劃問題轉化求解Karmarkar標準型的問題從可行解的多面體內部一個點出發，產生一個直接穿過多面體內部的點列，從而得到所需的最優解多項式時間算法是一種行之有效的多項式時間算法，但把一般的線性規劃問題轉化為Karmarkar標準型并不容易 原仿射尺度算法可以直接求解線性規劃問題在尋找迭代點的原理上與Karmarkar算法原理相似，但在確定何時停止迭代運用了線性規劃的對偶理論在理論上還未被證明是多項式時間算法實際效果優于Karmarkar算法，在中大規模的線性規劃問題上，它們的求解效率優于單純形法

[1] 張建中，許紹吉. 線性規劃[M]. 北京: 科學出版社，1990.

[2] 姚恩瑜，何 勇，陳仕平. 數學規劃和組合優化[M]. 杭州: 浙江大學出版社，2001.

[3] Papadimitriou H C，Steiglizt K.，Combinatorial optimization algorithms and complexity[J]. Printice-Hall,1982.

[4] P.GaCs and L.Lovasz. Khachian’s algorithm for linear programming[J]. Math,Programming Study 14 (1981): 61-68.