塔影效應引起的風電機組輸出功率波動問題

張弘鯤,孟祥星

（1.華北電力大學,北京 102206;2.黑龍江省電力有限公司,黑龍江 哈爾濱 150090）

由于風電機組的輸出功率與風速的3次方成正比,而風速具有隨機變化的固有特性,因此,風電機組的功率輸出也是不穩定的,這種不穩定的功率注入電網,尤其是在大規模風電場并網的情況下,將對電網的穩定性和電能質量造成影響。對風電機組輸出功率的波動性進行研究,不論從維持系統穩定還是從保證電能質量的角度都具有實際意義。

風電機組輸出功率的波動來源于風電機組運行過程中非恒定的轉矩,該轉矩的不穩定不但與風速的變化（如陣風、漸變風等）有關,而且還受機組自身固有特性的影響（如塔影效應、偏航誤差及風剪切作用等）,嚴重時這些因素將使風電機組的轉矩偏差達到20%[1、2],并且風電機組輸出功率的波動周期與葉片旋轉周期具有對應關系[3-5]。對于3葉片風電機組來說,轉矩的波動頻率是葉片旋轉頻率的3倍,由此引起的輸出功率波動頻率也是葉片旋轉頻率的3倍。

為從理論上對由于塔影效應和風剪切引起的風電機組輸出功率波動性進行分析,建立了相應的風速模型和風電機組模型,但多數文獻對此進行描述時,僅定性說明了這些作用對風速的影響,或建立了含有一些經驗參數的極坐標下的風速模型[1],不具有普遍適用性。因此,結合其他文獻的研究成果,建立了描述塔影效應和風剪切效應的風速模型,并結合某恒速風電機組數據和相關模型,對風電機組輸出功率的波動問題進行了計算分析。

1 風速模型

風電機組是將風能轉換成電能的中間環節,對風速的準確描述是研究風電機組輸出特性的基礎工作之一。鑒于本文的研究目的,僅為說明塔影效應和風剪切等作用對風電機組功率輸出的影響問題,將機組輪轂高度處的自然風速視為已知的恒定值,而將風電機組各葉片在塔影效應和風剪切作用下的等效風速作為輸入量進行分析,等效風速用于產生風力機的機械力矩。

風力機的葉片在旋轉過程中,在不同的位置處所面對的風速是不同的,這是風速垂直梯度變化的結果。風速在垂直方向上的變化也稱為風剪切,可表示為

式中 H——風電機組的輪轂高度;

z——距離地面的高度;

v（H）、v（z）——分別表示機組輪轂處和距離地面高度z處的風速;

α——風剪切指數。

雖然可以根據地表粗糙程度對α進行數學描述,但一般都是通過實測求出其大小。實測表明指數α并非常數,而是隨時間、風速及溫度的變化而變化,有時還會出現負值[3、4],這種變化將影響風電機組輸出功率。本文模型中將α視為正的常數。

風剪切對輪轂高度處等效風速的影響可按公式（2）計算[4]：

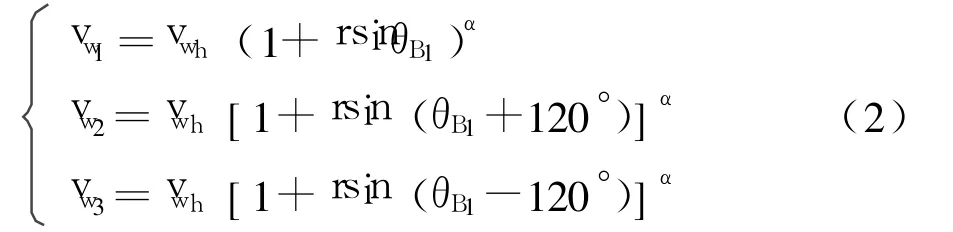
式中 vwh——輪轂高度處的風速,認為是常數;

vw1、vw2、vw3——分別為1號、2號、3號葉片風速;

θB1——1號葉片的旋轉角度,是時間的函數;

r——輪轂到葉片頂端3/4距離與輪轂高度

之比。

由于塔筒的影響,風在經過塔筒時會產生風向和風速的改變,進而造成風力機轉矩的變化,這種效應就是塔影效應。塔影效應對葉片的影響可以等效為葉片經過塔筒時風速的降低[6],其示意圖如圖1所示。其中θB表示葉片的旋轉角度,2δ為受塔影效應影響的角度范圍,Δvw為風速的降低量。考慮塔影效應后,每個葉片經過塔筒時都將產生一個降低的風速,此時等效輪轂高度處的風速表示為v′w1、v′w2和v′w3。在風力機傾角為5°時塔筒前的風速約降低30%,而隨著傾角的減小風速有所降低。受塔影效應影響的角度約在60°以內[7]。本文風速模型中將這2個量分別取為30%和60°,并假定風速的降低符合正弦規律變化。

圖1 塔影效應的等效風速示意圖

通過上述分析可以看出,風電機組3個葉片的等效風速都是葉片旋轉角的函數,隨時間而變化。輪轂高度處的等效風速可表示為

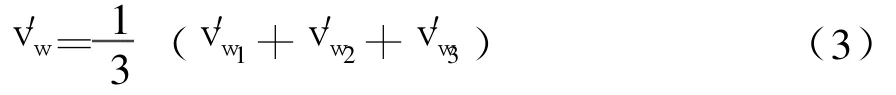
相應的轉矩可由公式（4）計算

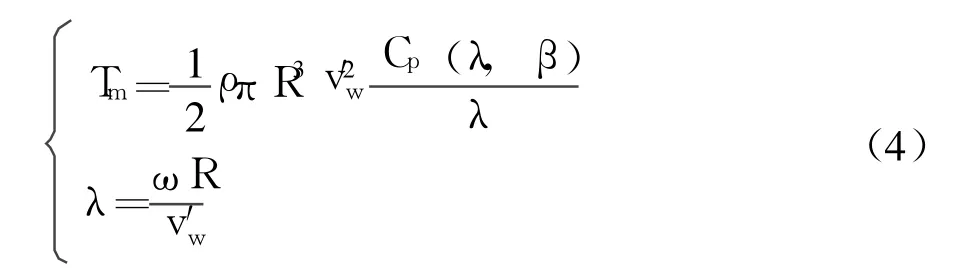
式中 ρ——空氣密度;

λ——葉尖速比;

R——葉片旋轉半徑;

ω——葉片旋轉角速度。

功率系數Cp與葉尖速比λ及槳距角β有關。

式（2）、式（3）及圖1構成了含有塔影效應和風剪切效應的風速模型,可以看出等效風速v′w隨葉片旋轉角變化而變化,因此,轉矩也是隨葉片旋轉角變化而變化。

2 算例分析

為便于對風剪切和塔影效應影響的理解,以額定容量500 kW的MADE-AE41型風電機組（恒速）為例進行分析,有關參數如表1所示。

表1 MADE-AE 41型風電機組的風力機參數

對于每個平均風速,都有一個平衡轉矩與其對應,即風電機組在該風速下的電磁轉矩和機械力矩達到平衡。MADE-AE41型風電機組的平衡轉矩與風速關系曲線如圖2所示[1]。

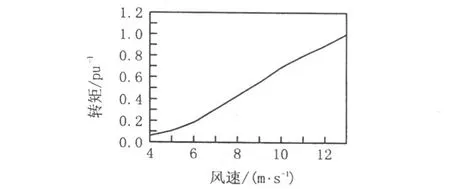
圖2 平衡轉矩與風速關系曲線

根據風速模型編制考慮塔影效應和風剪切效應的等效風速計算程序及圖2曲線的擬合函數形式,可以計算出不同效應下的風速變化規律及不同平均風速下風電機組的轉矩變化。假定風剪切指數為典型值（α=1/7）,并取輪轂高度處的自然平均風速為v=10m/s,計算得到的單葉片風速的變化曲線如圖3、圖4所示。

圖3為僅考慮風剪切后的單葉片風速變化規律,圖4為同時考慮風剪切和塔影效應后的單葉片風速變化規律。可以看出,塔影效應對作用到葉片上的風速的影響要比風剪切的作用大得多,風速的變化主要來源于塔影效應。

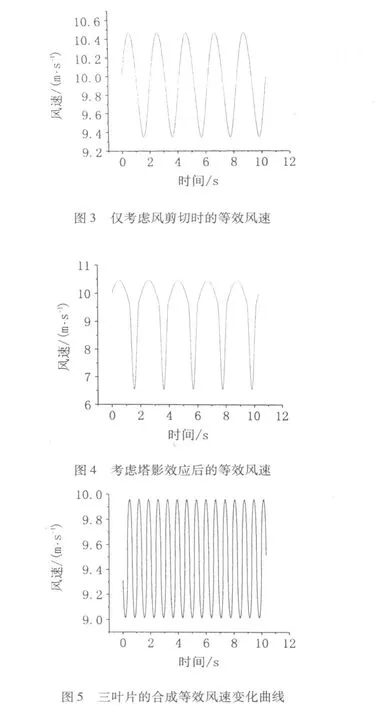
三葉片的合成風速如圖5所示,與單葉片相比三葉片合成風速的波動幅度有所降低,而波動頻率增大為原來的3倍,即達到3p頻率;同時總的等效平均風速也有所降低,約達到v=9.5 m/s。因此,風剪切和塔影效應不但使風電機組輸出功率產生波動,而且還將使總的輸出功率降低。根據圖2曲線可以看出對應v=9.5m/s時的轉矩約比v=10 m/s時降低10%,即風電機組的輸出功率也有約10%的損失。

需要指出的是,本文僅是用風電機組的平衡轉矩與平均風速的關系曲線對由于風速的變化造成的輸出功率降低進行估計,詳細的計算應該是建立風電機組的動態模型,結合本文風速模型可以得出相對精確的功率變化規律。

3 結論

a.本文考慮塔影效應和風剪切作用后的等效風速模型,可以用于風電機組輸出功率的仿真計算,計算結果準確程度與風電機組類型及其模型有關。

b.塔影效應對風電機組輸出功率的影響比風剪切作用大很多,風電機組輸出功率的波動主要來源于塔影效應。

c.風剪切和塔影效應使恒速風電機組的輸出功率產生3p頻率的波動,且在數值上降低一定幅度。

[1] H.Armaris,C.Vilar,et al.,Frequency domain analysis of flicker produced by wind energy conversions systems,Paper accepted for presentation at the 8thinternational conference on harmonics and quality of power ICHQP'98,jointly organized by IEEE/PES and NTUA,Athens,Greece,October 14-16, 1998.

[2] Carolina Vilar Moreno,Hortensia Amaris Duarte,Julio Usaola Carcia,Propagation of flicker in electric power networks due to wind energy conversions systems,IEEE Transactions on energy conversion,Vol.17,No.2,June 2002.

[3] Torbj?rn Thiringer,Jan-?ke,Dahlberg,Periodic power pulsations from a three-bladed wind turbine,www.elkraft.chalmers.se/Publikationer/EMKE.publ/Abstracts/A lsvik.pdf.

[4] Stephen B.Bayne,Michael G.Giesselmann,Effect of blade passing on a wind turbine output,Release A：Copyright 2000 by the American Institute of Aeronautics and Astronautics.

[5] M.Davidson,Interaction of a wind farm with the distribution network and itseffect on voltage quality, 1996 the institution ofelectrical engineers,Printed and published by the IEE,Savoy Place,London WC2R OBL.UK.

[6] M.P.Papadopoulos,S.A.Papathanassion,et al.Investigation of the flicker emission by connected wind turbines,Paper accepted for presentation at the 8thinternational conference on harmonics and quality of power ICHQP'98,jointly organized by IEEE/PES and NTUA,A thens,Greece,October 14-16,1998.

[7] John Olav Gi?ver Tande,Giorgos relakis et al.,Synchronisation of wind turbines,Wind power for 21stcentury,25-27 Sept.2000,Kassel,germany,Subject number：3,www. energy,sintef.no/prosjnyt/levkval/vindkrft/sync_paper01.pdf.

[8] Andres E.Feijoo,Jose Cidras,Modeling of wind farms in the load flow analysis,IEEE transactions on power systems,Vol. 15,No.1,February 2000.