基于LabVIEW的風電機組滾動軸承故障診斷系統及其仿真

徐浩凇，鄭小霞

（上海電力學院電力與自動化工程學院，上海 200090）

滾動軸承是風力發電機組的關鍵部件之一，其中最重要的齒輪箱滾動軸承和發電機滾動軸承都屬于經常發生故障的部件［1］.因此，研究滾動軸承的故障診斷對風電機組正常運行具有重要意義.

由于伴隨軸承故障的發生、發展，往往會引起信號頻率結構的變化，而根據此時的頻率可判斷軸承是否發生故障，并可以此確定故障類型.因此頻域分析是軸承故障診斷的有效方法.文獻［2］采用LabvieW設計的軟件平臺在時域和頻域內對軸承振動信號進行了故障診斷，但其頻域分析采用依賴硬件參數的共振解調方法，這使得LabvieW參數設置較為復雜.

本文采用基于特征參數的滾動軸承故障診斷方法，依據振動信號的峭度指標、峰值因數、偏態因數等參數對滾動軸承的內圈、外圈、滾動體進行故障識別，并提出了希爾伯特包絡譜分析的滾動軸承故障診斷方法，該方法在小波變換求得高頻系數的基礎上，用希爾伯特變換求取振動信號的包絡譜，從而確定軸承的故障類型.在LabVIEW 8.5環境下開發了基于特征參數和希爾伯特包絡譜分析法的風電機組滾動軸承故障診斷系統.故障診斷實驗結果表明，該系統能夠有效、快速、準確地對滾動軸承內圈、外圈、滾動體故障進行識別并報警.

1 基于特征參數滾動軸承故障診斷

對于一個有損傷的軸承，當滾動體接觸點進入缺陷區時，就會發生機械沖擊，沖擊脈沖幅度與損傷程度成正比.由于沖擊力的變動幅度很大，且帶有較大的隨機噪音，因此，用波形特征參數來表示沖擊波形幅度能有效反映軸承的故障狀態，這是軸承故障檢測中的常用方法［3］.

由于滾動軸承振動信號是隨機的，其本身不能直觀地反映系統狀態的變化，但通過統計分析，可以找到反映其統計規律的特征量.在信號的幅值上進行各種處理，即對信號的時域進行統計分析稱為幅域分析.幅域統計方法計算簡單、顯示直觀、容易理解，在簡易振動診斷中應用非常廣泛.常用的信號幅域統計參數包括有效值、峭度、峰值因數、偏態指標、峭度指標、裕度因數、脈沖因數、峰態因數等.

2 基于希爾伯特包絡譜分析的滾動軸承故障診斷

由于滾動軸承振動信號的不平穩特性，合理地選擇信號處理方法對于確保故障診斷系統的精確性很重要.不準確的信號分析會導致故障診斷系統多次錯誤報警，降低故障診斷的準確性［4］.

小波分析具有對信號的自適應性，能識別振動信號的突變成分;振動信號經希爾伯特變換后得到其包絡譜，由包絡譜獲得故障特征信息.由此可結合小波分析和希爾伯特變換二者的優點對軸承進行故障診斷.

2.1 滾動軸承特征頻率

滾動軸承的異常振動頻率由轉子的旋轉速度、損傷部位的形態，以及軸承元件的固有振動頻率所決定.轉子的旋轉速度越高、損傷越嚴重，其振動頻率就越高.滾動軸承故障的振動特征是：當發生異常時，頻譜豐富，不會只產生單一的特定頻率，各頻率分量的幅值顯著增大.由于軸承元件的固有頻率較高，通常在1×103～1×104Hz內，一旦某種元件出現異常激發該種固有頻率，頻譜中就會出現高頻成分.因此，利用軸承元件的固有頻率診斷故障是一種有效的方法［4］.

由于結構、運行特性不同，各零部件有不同的特征頻率.滾動軸承的特征頻率（即接觸激發的基頻）可以根據軸承元件之間滾動接觸的速度關系所建立的方程求得.用它計算的特征頻率值往往十分接近測量數值，因此在診斷前總是將其先計算出來，并以此作為診斷的依據.對于外圈固定的軸承，可運用下列公式計算出各元件的故障特征頻率.

內圈（外滾道）缺陷頻率為：

2.2 小波變換

對非平穩信號進行分析時，高頻信號需要采用小時間窗，而低頻信號需要采用大時間窗，即窗口大小應隨頻率變化而改變，但加窗傅立葉變換無法實現這一功能.小波分析是一種窗口大小固定但其時頻窗可以改變的時頻局部化分析方法，在低頻部分具有較高的頻率分辨率和較低的時間分辨率，在高頻部分具有較高的時間分辨率和較低的頻率分辨率.正是這種特性，使小波分析具有對信號的自適應性，能識別振動信號的突變成分［5］.

小波變換的基本思想與傅里葉變換是一致的，它也是用一族函數去表示信號或函數，這一族函數稱之為小波函數系.小波函數系是由一基本小波函數的平移和伸縮構成的.與傅里葉變換相比，小波變換是時間（空間）頻率的局部化分析，它通過伸縮平移運算對信號（函數）逐步進行多尺度細化，最終達到高頻處時間細分，低頻處頻率細分，能自動適應時頻信號分析的要求，從而可聚焦到信號的任意細節，解決了傅里葉變換中存在的難題.有人把小波變換稱為“數學顯微鏡”.

小波定義過程如下.

對于任意ψ（t）∈L2（R），即ψ（t）是平方可積函數，如果ψ（t）的傅里葉變換滿足可容許條件：

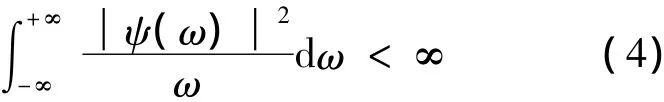
則稱ψ（t）是一個基本小波或母小波函數.

在多數情況下，要求ψ（t）連續且有一個矩為零的大整數M，也即對所有整數m＜M，有：

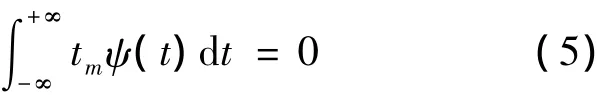
這表示母小波必須非零且均值為零.

母小波ψ（t）縮放（或稱膨脹）α倍并平移b得到：

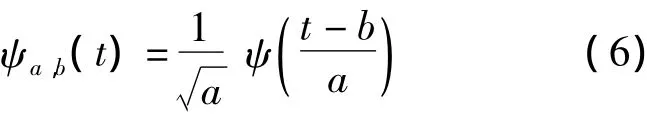
人們稱ψa，b（t）為小波基函數，也稱小波.它是由一個母小波函數經過伸縮與平移所產生的二維空間的基底，依賴于參數a和b.其中a被稱為尺度因子（參數），b被稱為時移因子（參數）.尺度參數a改變小波的形狀，時移參數b改變小波的位移.

2.3 希爾伯特包絡譜

軸承的許多故障信息是以調制的形式存在于所監測的振動信號之中，如果借助希爾伯特變換對這些信號進行解調處理，就能方便地獲得故障特征信息，以確定軸承所發生的故障類別.希爾伯特譜是信號的幅值隨時間和頻率變化的精確描述［5］.包絡分析的寬頻帶特性常引起系統固有頻率處的諧振，從而在該頻率附近形成以特征故障頻率為基頻的邊帶，此邊帶是故障信號調制的結果，因此包絡分析又稱為解調分析.通過對包絡信號進行頻率分析，能比較精確地確定故障發生的部位和層次.

希爾伯特解包絡的原理就是讓測試信號產生一個90°的相移，從而與原信號構成一個解析信號，求出的解析信號就構成了包絡.希爾伯特解包絡的原理如圖1所示.

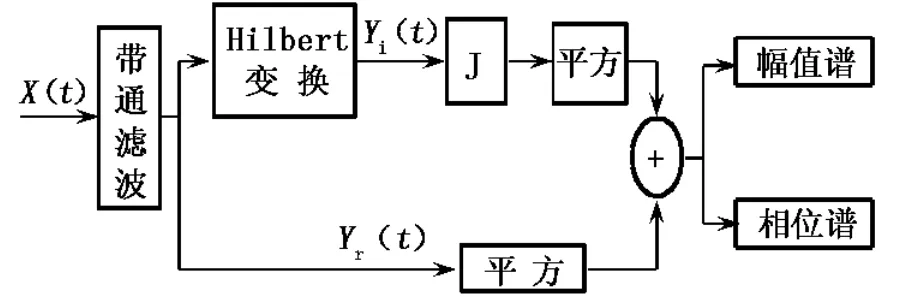
圖1 希爾伯特解包絡原理

X（t）為振動加速度信號，帶通濾波后得到信號yr（t），yr（t）經過希爾伯特變換后得到信號yi（t），二者構成解析函數式Z（t），即：

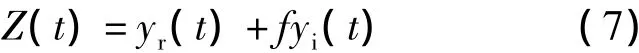
由此得到振動信號的幅值調制信號為：

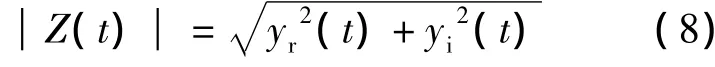
上述過程完成了對信號的解包絡分析.

3 基于LabVIEW的風電機組滾動軸承故障診斷系統的開發

LabVIEW是美國國家儀器（NI）公司推出的使用最為廣泛的虛擬儀器計算機語言.在特征參數故障診斷和希爾伯特包絡譜分析故障診斷的基礎上，利用LabVIEW平臺建立了風電機組滾動軸承故障診斷系統，主要包括振動信號的數據處理模塊、故障診斷模塊、數據存儲模塊、系統時間模塊，以及顯示面板等部分，總體結構如圖2所示.

基于LabVIEW的風電機組滾動軸承故障診斷系統的程序示意如圖3所示.

LabVIEW很重要的一個優勢就是界面編輯的所見即所得.用其構建的顯示面板形象生動，布局靈活性強.基于LabVIEW的風電機組滾動軸承故障診斷系統前面板如圖4所示.

由圖4可知，該系統實現了故障報警、波形顯示、特征參數顯示、特征頻率顯示、故障部位顯示、保存數據、系統時間顯示和希爾伯特包絡譜顯示等功能.

圖2 基于LabVIEW的風電機組滾動軸承故障診斷系統的功能模塊

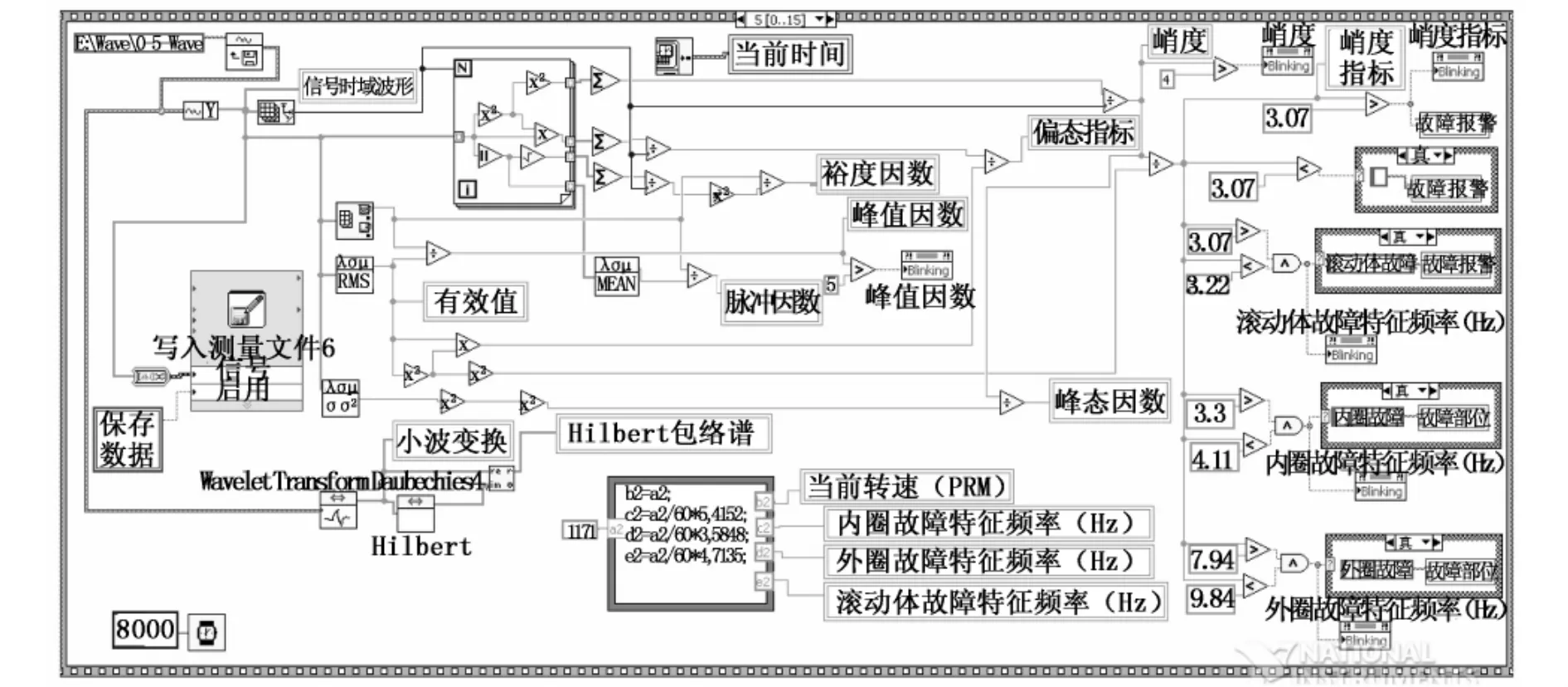
圖3 基于LabVIEW的風電機組滾動軸承故障診斷系統的程序示意

4 故障診斷系統仿真研究

故障診斷仿真實驗采用美國凱斯西儲大學（CWRU）軸承數據中心的滾動軸承故障數據（http：//www.eecs.cwru.edu/laboratory/bearing）.本次實驗數據選取滾動軸承驅動端在746 W的電機負載下，外圈故障點的方向與負載區方向垂直，軸承轉速1 771～1 797 r/min，采樣頻率為48 000 Hz，通過放電加工（Elecctric Discharge Machining，EDM）技術，在內滾道、外滾道和滾動體上人為制造的直徑0.533 4 mm，深度為0.279 4 mm的軸承故障.采樣序列數據長度為1 024點，振動信號由與磁性基座相連的加速度傳感器獲取.

由于篇幅限制，本文僅以軸承外圈故障的診斷為例.選取軸轉頻fs=29.5 Hz，采樣序列長度為1 024點的外圈故障數據.外圈故障特征頻率計算經驗公式為：fo=3.584 8×fs，將fs=29.5 Hz代入公式，得fo=105.8 Hz.

利用該故障診斷系統對滾動軸承外圈故障診斷結果如圖5所示.

從圖5中可直觀地看出，故障報警燈呈報警狀態的同時，峭度指標為8.89且閃爍提示，外圈故障特征頻率值為105.81 Hz并閃爍提示;故障部位提示區醒目顯示：外圈故障;從信號時域波形圖上可以看出此時沖擊較為強烈，小波變換所得的高頻系數呈離散狀分布，且沖擊很強，希爾伯特包絡譜最大脈沖對應頻率105 Hz和210 Hz正是軸承外圈故障特征頻率和其2倍頻，由此頻率也可推斷軸承外圈出現故障.

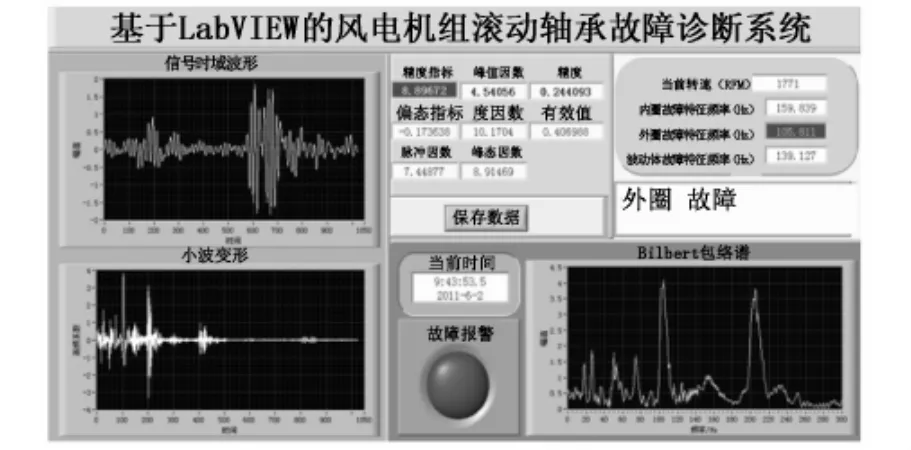
圖5 滾動軸承外圈故障診斷結果

5 結語

本文在LabVIEW 8.5環境下實現了基于振動信號特征參數和希爾伯特包絡譜分析的兩種故障診斷方法，開發了風電機組滾動軸承故障診斷系統.該系統的前面板形象生動，實現了故障自動報警、故障類型顯示、特征頻率顯示閃爍報警、希爾伯特包絡譜顯示，以及數據存儲等功能.故障診斷實驗結果表明該系統可以直觀、準確、迅速地診斷出滾動軸承外圈、內圈、滾動體的故障.

［1］任臘春，張禮達.基于模糊理論的風力機故障診斷專家系統的研究［J］.流體傳動與控制，2009（6）：10-12.

［2］蘇敏，王勇，何惜港.基于LabVIEW的滾動軸承故障診斷系統［J］.軸承，2010（9）：41-44.

［3］MCFADDEN P D，TOOZHY M M.Application of synchronous averaging to vibration monitoring of rolling element bearings［J］.Mechanical Systems and Signal Processing，2000，14 （6）：891-906.

［4］DANESHI Far D，CAPOLINO G A，HENAO H.Review of failures and condition monitoring in wind turbine generators［C］//XIX International Conference on Electrical Machines，2010，Rome，2010：1-6.

［5］趙玉菊，陳恩利，史振江.基于小波包絡分析的滾動軸承故障診斷研究［J］.石家莊鐵路職業技術學院學報，2009，8 （4）：36-41.

（編輯蘇娟）