基于小波包變換的電力系統諧波檢測

劉蓉暉

（上海電力學院電力與自動化工程學院，上海 200090）

諧波不僅使電力設備損耗增加，導致繼電保護和自動化裝置誤動作，引起電氣諧振和電機的機械振動，而且還會干擾通信線路，影響測量儀表的精度，甚至造成電網的大事故.因此，對電力系統的諧波進行有效治理，具有明顯的社會經濟效益［1］.諧波檢測是實現諧波治理的前提條件，諧波檢測已成為當前國內外電能質量檢測研究的熱點之一.

目前，電力系統中的諧波檢測方法大多是基于快速傅里葉變換（FFT）及其改進算法.傅里葉變換具有良好的頻域分析和時域無局部化特性，因此只適合穩態諧波的檢測.而小波變換方法具有良好的時頻局部化特性，很適合檢測突變信號和非平穩信號［2］.但小波變換具有對信號頻帶劃分不均勻、對高頻信號檢測精度不高，以及高頻頻帶寬、低頻頻帶窄的特點.小波包分析可以實現頻帶的均勻劃分，具有比小波變換更好的時頻特性和較高的信號檢測精度［3］.

1 小波變換

對于任意的函數x（t）∈L2（R）的連續小波變化（CWT）為：

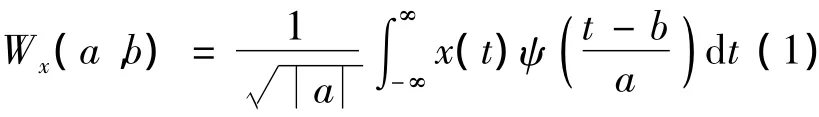
式中：ψ（t ）——基本小波（母小波）;

a，b——小波函數的尺度因子和位移參數，分別決定小波的時頻窗在頻域和時域的位置.這里的a和b是連續變化的，稱為連續小波變換.

小波變換具有對信號的自適應性.在低頻部分具有較高的頻率分辨率和較低的時間分辨率，在高頻部分具有較高的時間分辨率和較低的頻率分辨率，所以也被稱為數學顯微鏡［4］.

實際的觀測信號都是離散的，而且由于計算機處理的是離散量，所以信號處理中都采用離散小波變換（DWT）.多數情況下是將尺度因子a和位移參數b按2的冪次進行離散.最有效的計算方法是由MALLAT S于1988年提出的基于多分辨率分析的快速小波算法，又稱Mallat算法.

Mallat快速小波變換是利用正交小波基將信號分解為不同尺度下的各個分量，其實現過程相當于重復使用一組高通和低通濾波器將信號逐步分解.第一步是將信號分解為通過高通濾波器產生的高頻細節分量和通過低通濾波器產生的低頻近似分量.低頻分量和高頻分量所占頻帶寬度相等，各占信號的一半頻譜帶.第二步是對低頻分量重復上述過程進行進一步分解，從而得到下一層次上的兩個分解分量，而高頻分量不再進行分解.以下再依此類推分解.由于小波變換對信號頻帶的劃分不是均勻劃分，因此信號的低頻部分能夠得到精確分解，但在高頻段的頻率分辨率較差.

2 小波包變換

小波包變換是建立在小波變換的基礎上的，它可以實現頻帶的均勻劃分，對小波變換中沒有細分的高頻分量作進一步分解，并能夠根據被分析信號的特征，自適應地選擇相應頻帶，使之與信號頻譜相匹配，以提高時頻分辨率.

2.1 小波包基本原理

設x（t）為待分析時間信號，P（i，j）表示第i層（即尺度因子為2i）上的第j個小波包，稱為小波包系數.H和G為小波包分解低通和高通濾波器.小波包分解的快速算法為［5］：

2.2 小波包的頻帶劃分

現有的小波包分解結構，各個頻帶標記的大小與相應的頻帶頻率大小不完全對應.這樣就對諧波的頻率分析帶來困難，不能根據小波包分解的結果直接判斷諧波頻率范圍，不利于諧波檢測分析.文獻［6］提出了一種新的小波包分解結構，即將低通和高通濾波器的排列重新調整，就可以得到按頻率大小順序連續分布的均勻頻帶.若將信號中的最高頻率看作是1，進行5層小波包分解，則可將整個信號頻帶分成連續順序的32個子頻帶，每個子頻帶帶寬為1/32=0.031 25.新的小波包濾波器組結構及其頻段劃分見圖1.

待分析信號X經過第1層小波包分解，通過低通濾波器H的信號頻帶范圍為0～0.5，通過高通濾波器G的信號頻帶范圍為0.5～1;將這兩組信號進行第2層小波包分解，濾波器組排列順序依次為低通濾波器H，高通濾波器G，高通濾波器G和低通濾波器H;以此類推.按照圖1所示的濾波器排列順序，經過第5層小波包分解后的32個子頻帶的頻率范圍依次為0～0.031 25，0.031 25～0.062 5，…，0.968 75～1，因此不同頻帶的小波包系數就相當于從某個時-頻窗內提取到的原始信號信息.

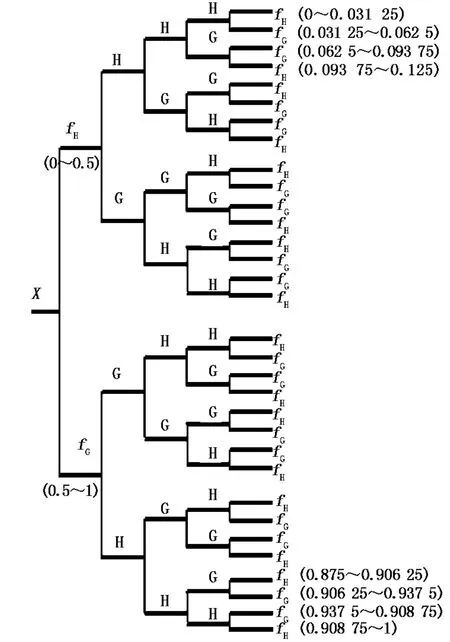
圖1 新的小波包濾波器組結構及其頻段劃分

3 仿真實例驗證

3.1 電力系統穩態諧波的檢測

以三相橋式整流電路在電感性負載時交流側的電流作為諧波信號進行檢測.該信號為正負半周各120°的近似方波，其數學表達式為：

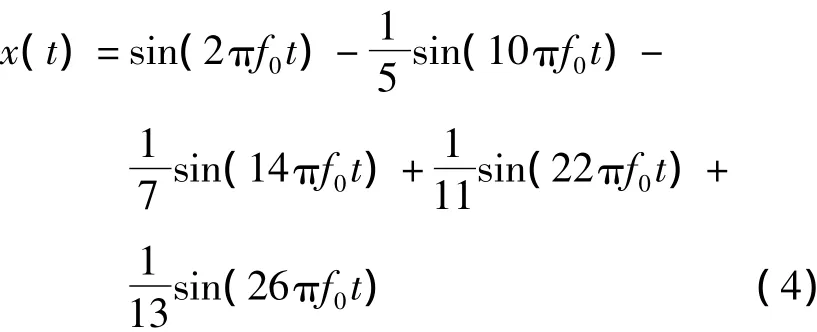
式中：f0=50 Hz，諧波的幅值采用標幺值.此諧波信號中，除了頻率為50 Hz的基波之外，還包括5次、7次、11次和13次諧波.下面用Matlab7.4軟件提供的小波分析工具箱進行仿真.

本文采用正交小波db40，因為db40小波的分解與重構信號失真度小，具有良好的計算性和時域光滑性.對原始信號x（t）進行5層小波包分解，采樣頻率為6 400 Hz;每個基波周期采樣128點，采樣時間為6個基波周期.整個頻帶分解成25=32個子頻帶，每個子頻帶寬1/32×3 200= 100 Hz.原始信號x（t）通過5層小波包分解，被分離到各個子頻帶中，計算第5層小波包分解系數的重構信號，得到第5層第j個小波包系數的重構信號，小波包分解結點為（5，0），（5，1），（5，2），（5，3），（5，4）（5，5），（5，6），（5，7）的小波包重構信號頻率范圍及諧波次數見表1.原始信號和重構信號的波形見圖2.

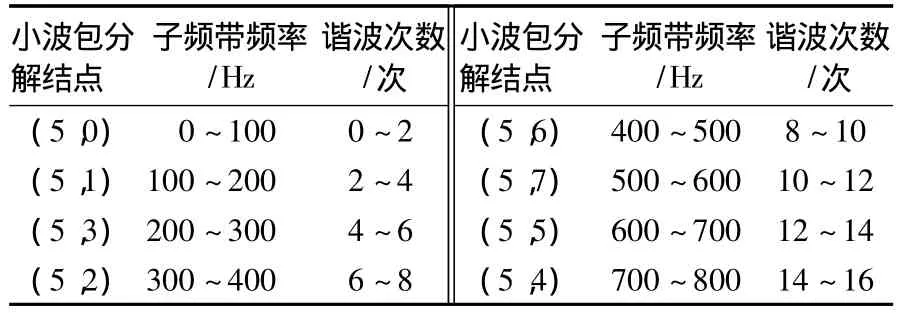
表1 小波包重構信號的頻譜范圍

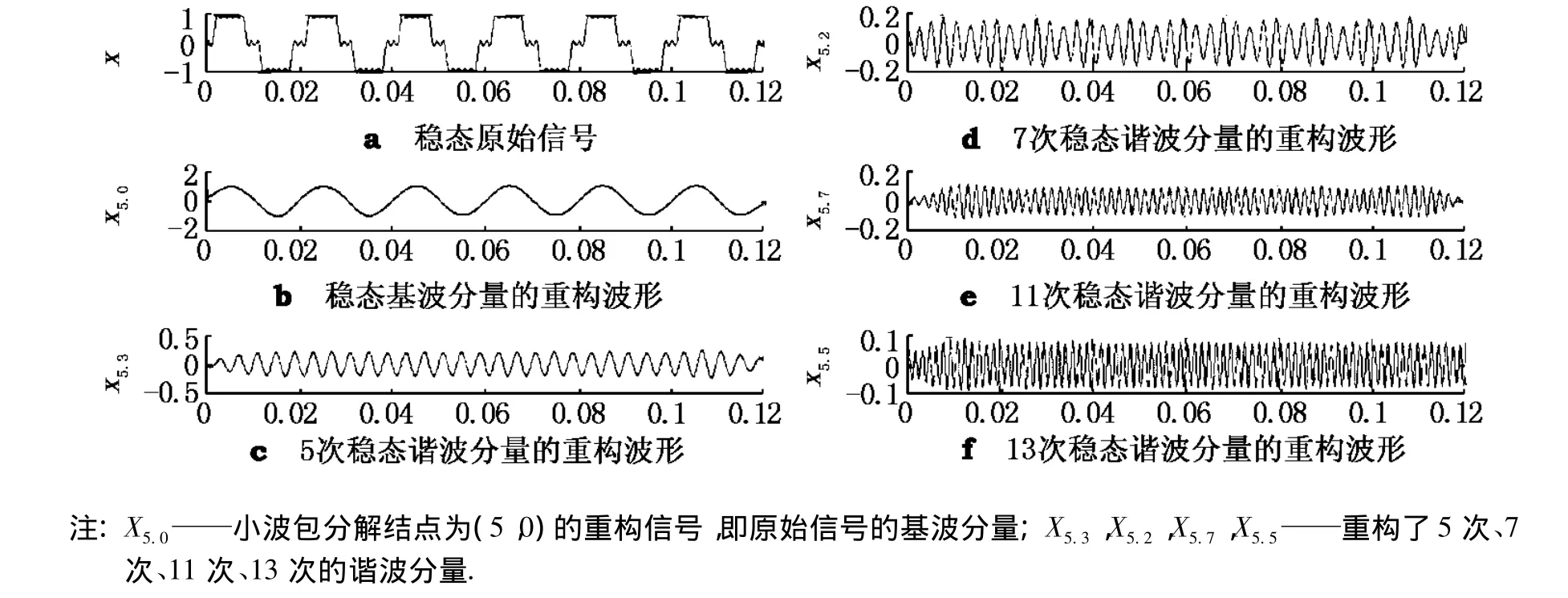
圖2 小波包變換對穩態諧波信號的重構波形

由圖2可知，所得波形與理論波形相同.由此可見，小波包重構信號可以將原始信號在各個子頻帶有效分離出來.

3.2 電力系統暫態諧波的檢測

某電力系統暫態諧波信號的數學表達式為：

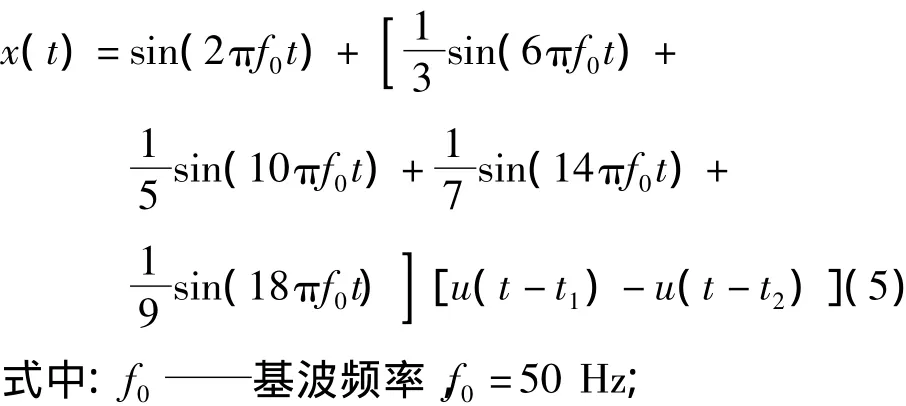
t1起始時間，t1=0.1 s;

t2結束時間，t2=0.2 s.

選用db40小波對原始信號進行5層小波包分解，采樣頻率為6 400 Hz，采樣周期12個.該信號的基波頻率為50 Hz，在采樣的第6至第10個周期出現了3次、5次、7次和9次諧波.其仿真試驗結果見圖3.

由圖3可知，X5.0完美地重構了原始信號的基波，X5.1，X5.3，X5.2，X5.6重構了原始信號的3次、5次、7次和9次暫態諧波，根據波形可以得到暫態諧波的起止時間分別為t1=0.1 s，t2=0.2 s，與理論值一致.

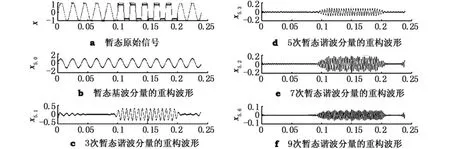
圖3 小波包變換對暫態諧波信號的重構波形

4 結論

（1）小波包變換具有良好的時頻局部化特性，對信號頻帶可以實現均勻劃分，適用于電力系統諧波的檢測.

（2）仿真試驗表明，通過小波包變換可對電網中的穩態諧波和暫態諧波進行準確分析，能為電網中諧波的研究和治理提供依據.

［1］任震.小波分析及其在電力系統中的應用［M］.北京：中國電力出版社，2003：12-36.

［2］任震，黃群古.基于多頻帶小波變換的電力系統諧波分析新方法［J］.中國電機工程學報，2000，11（2）：38-41.

［3］薛惠，楊仁剛，羅紅.利用小波包變換實現電力系統諧波分析［J］.電網技術，2004，28（5）：41-45.

［4］胡昌華，李國華，周濤.基于MATLAB 7.x的系統分析與設計小波分析［M］.西安：西安電子科技大學出版社，2008：20-69.

［5］徐劍，金之儉，傅堅，等.基于改進小波包算法的變壓器繞組變形的檢測［J］.華東電力，2010，38（3）：376-380.

［6］PHAM V L，WONG K P.Antidistortion method for wavelet transform filter banks and nonstationary power system waveform harmonic analysis［J］.IEE Proceedings Generation，Transmission and Distribution，2001，148（2）：117-122.

（編輯胡小萍）