Kalman濾波在Yule-Walker譜估計中的應用

侯杰虎

（成都理工大學信息工程學院，四川成都610000）

1.引言

功率譜估計是數字信號處理的主要內容之一，主要研究信號在頻域中的各種特征，目的是根據有限數據在頻域內提取被淹沒在噪聲中的有用信號，將其廣泛用于民用通信和軍事通信中。現代譜估計主要是針對經典譜估計的分辨率差和方差性能不好的問題而提出的。現代譜估計從方法上大致可分為參數模型譜估計和非參數模型譜估計兩種[1]，前者有AR模型、MA模型、ARMA模型、PRONY指數模型等；后者有最小方差方法、多分量的MUSIC方法等。

在信號的傳輸過程中，會不可避免地存在著各種噪聲干擾，這些噪聲將對我們的功率譜估計的分析結果產生直接的影響。目前，常用的噪聲去除方法有小波去噪、中值或均值濾波、傅里葉變換濾波等，但是上述方法都存在著一定的缺陷，如穩定性較差，去噪能力有限或者不能很好地解決尖刺問題。針對此現象，信號學家D.Evensen首次提出將kalman濾波應用到信號處理中[2]。

本文主要討論在平穩隨機過程中用自相關法估計AR模型參數，進而實現功率譜估計的Yule-Walker算法進行加入kalman濾波的改進，從而達到減小譜估計誤差，提高計算結果的穩定性。

2.Yule-Walker譜估計算法

參數不隨時間變化的系統稱為時不變系統。相當多的平穩隨機過程都可以通過用白色噪聲激勵一線性時不變系統產生[3]，而線性系統又可以用線性差分方程進行描述，這種差分模型就是自回歸－滑動平均（ARMA）模型。設平穩隨機序列x(n)(n=0，1…，N-1)的AR(p)模型為

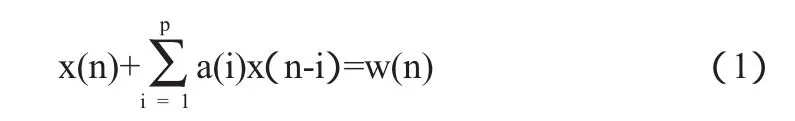
其中a(i)(i=1，2，…，p)是AR系數，w(n)是均值為零、方差σ2為的白噪聲。

Yule-Walker方程的舉證表達式如下：

其中Rxx(m)是相關系數，｛a(1),a(2),…，a(p)｝是AR(p)模型的系數，σ2是預測誤差功率[4]。

在信號序列x(n)的(p+1)個自相關函數值Rxx(0)，Rxx(1)，…，Rxx(k)已知的情況下，通過萊文森-德賓算法經過階次遞推，可依次計算出{a1(1),σ1}，{a2(1),a2(2),σ2}，…，{ap(1),ap(2)，…，ap(p)σp}其中AR模型參量都加了下標以表明階數，階數為p的最后那組參量就是方程的解，具體算法如下：

最后通過計算得到p階預測誤差濾波器的系數{a(1),a(2),…,a(p)}和相應的預測誤差σ2，再利用公式

求得x(n)的功率譜估計。如果我們已知的是x(n)的N個值{x(0)，x(1)，…，x(N-1)}，而不是x(n)的(p+1)個自相關函數值。為了用Yule-Walker方程求得AR(p)模型的系數和相應的預測誤差σ2，我們必須首先按式（9）計算x(n)的自相關函數值，最后再進行譜估計。

3.譜估計中kalman濾波器的設計

kalman濾波算法是一個從觀測變量得到最優狀態估計和狀態觀測的最優化自回歸數據處理算法，對于解決很大部分的問題，是最優、效率最高甚至是最有用的[5]。其基本思路如下：首先建立隨機動態變量隨時間變化的先驗模型，然后通過觀測得到觀測變量，利用卡爾曼方程組獲得目標狀態基于全局信息的的最優估計值。這樣估計的實際意義為：對于一輸入未知的體系，可根據觀測輸出Z(k)、體系特征和統計性質來最佳地估計輸入X(k)。正是因為kalman濾波器具有自適應特性以及預測和校正功能，使其在計算中對觀測數據和噪聲無過多具體要求，具有較強的容錯能力。

首先，引入一個離散控制過程的系統。該系統可用一個線性隨機差分方程（Linear Stochastic Difference equation）來描述：

再加上系統的測量值：

上兩式子中，X(k)是k時刻的系統狀態，U(k)是k時刻對系統的控制量。A和B是系統參數，對于多模型系統為矩陣。Z(k)是k時刻的測量值，H是測量系統的參數，對于多測量系統，H為矩陣。W(k)和V(k)分別表示過程和測量的噪聲，并假設為高斯白噪聲(White Gaussian Noise)，其協方差分別是Q，R（這里設W(k)和V(k)不隨系統狀態變化而變化且相互獨立）。

本文將通過萊文森-德賓算法得到的AR(p)模型系數作為濾波器的最初狀態值X(k)，高斯白噪聲作為觀測噪聲，并通過隨機序列x(n)和Yule-Walker方程得到的觀測值Z(k)，對式（10），（11）進行kalman濾波得到狀態預測方程：

預測狀態下的協方差方程

濾波器增益方程

狀態最優化估計方程

狀態最優化估計的協方差方程

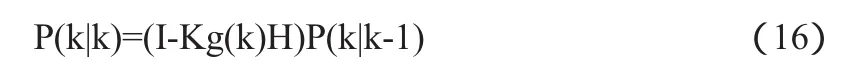
最終，本文通過上述式（10）～（16）以及已知的AR(p)模型系數、高斯白噪聲、觀測值、kalman濾波迭代運算中不斷被更新的增益值計算得到X(k)的最優估計值，以得到的最優AR模型系數來進行譜估計，達到降低由于在譜估計中平穩隨機序列數量問題而引起的誤差的目的。

4.實驗結果分析

沒有經過kalman濾波器的Yule-Walker功率譜估計結果如圖1所示，在相同條件下，在Yule-Walker功率譜估計中引入kalman濾波器的結果如圖2所示。可以看出，圖1中真實值與估計值相差較大，而在圖2中真實值與估計值的差異較圖1有所減小。為了直觀度量真實值與估計值的誤差，本文通過公式

來計算兩種方法的功率譜誤差協方差。其中Perr為系統響應的譜估計誤差，Pest為譜估計值，Ptrue為真實值，σerr為譜估計誤差Perr的協方差。

無kalman濾波器的功率譜誤差協方差σerr=1.5285，加入kalman濾波器的功率譜誤差協方差σerr=1.0059，可見加入kalman濾波器后提高了譜估計的精度和穩定性。

圖1 功率譜估計值與真實值的比較

圖2 加入kalman濾波器的功率譜估計值與真實值的比較

5.結束語

Yule-Walker功率譜估計算法之所以有一定的誤差與其平穩隨機序列x(n)中的n值和生成隨機序列時的噪聲有關，n值越大，其誤差越小，但當n值增大到一定程度后，誤差不再減小。而kalman濾波器通過其不斷的預測和修正，努力使最后的估計值達到最優化。相對受白噪聲的影響大大減小，增加了計算結果的穩定性，且kalman濾波器的自適應特性使其具有較強的容錯能力，能提高計算的精度。因此kalman濾波器在對于信號處理中的譜估計會有很好的應用前景。

[1] 李英民，董銀峰，賴明.地震動瞬時譜估計的Unscented Kalman濾波方法[J].應用數學和力學，2007:1370-1377.

[2] BUEHNER M，GAUTHIER P，LIU Z.Evalution of new estimates of background and observation error co-variances for variational assin ilation[J].Quart J Roy Meteor Soc，2006:3373-3383.

[3] 張賢達.現代信號處理(第二版)[M].清華大學出版社，2002.

[4] 吳順君.近代譜估計方法[M].西安電子科技大學出版社，1994.

[5] MOHINDER S.GREWAL，ANGUS P.ANDREWS.Kalman Filtering:Theory and Practice[M].A Wiley-Interscience Publication，2001.