一種新模板的圖像邊緣提取方法

劉煜，劉巖，呂淑靜

(1.西安國家民用航天產業基地管委會衛星應用產業促進局，陜西西安710100;2.第二炮兵工程學院電子技術教研室，陜西西安710025;3華為西安研究所網絡產品線，陜西西安710075)

提出了一種基于新模板的圖像邊緣提取算法，算法依據梯度算子模板的思路，但完全不同于梯度算子，梯度算子是通過模板在待處理圖像上按一定規則的遍歷，即卷積。首先得到圖像的灰度梯度，再設定局部、全局或是自適應閾值，對灰度梯度進行過濾、二值化，得到了圖像的邊緣。算法的基本原理是:通過設定的水平或垂直模板，與待處理圖像進行遍歷矩陣相乘，得到圖像中相鄰像素間的灰度差，接著取定閾值，當灰度差大于該閾值時，將作為灰度差中被減數的像素值賦1，當灰度差小于或等于該閾值時，將相應像素值賦0，即二值化后便得到了圖像的邊緣［1－3］。

1 縱向模板算法

由算法原理可以看出，本算法最為關鍵的就是模板的選取。現在選定一個3×3的縱向模板

設G為待處理圖像，當MZ3×3在G上遍歷相乘時有

式(2)中“?”表示遍歷相乘，注意到結果矩陣的第m－1行和第m行中各對應元素絕對值相等且互為相反數，這是因為m行是結果矩陣的最后一行，無法向下相減，便用向上相減替代之。因為圖像中相鄰元素間屬性的相似性，所以這種替代是合理的。用表示式(2)矩陣中的元素，其中1≤i≤m，時，將aij的灰度值置為，將aij的灰度值置為0，這樣就得到了采用縱向3×3模板算法時圖像G的多像素二值邊緣圖。所謂的縱向模板算法，是指MZ3×3在圖像G上遍歷矩陣相乘后，得到的是G的縱向灰度差，即相鄰行之間的灰度差。式(2)中M為選取的閾值，采用類間方差最大化閾值分割算法(Otsu)得到［4－7］。

采用Matlab語言編程、選擇某機場下視景圖像對提出的縱向3×3模板算法進行計算機仿真實驗。圖1(a)為265×351的某機場原始的下視景圖像，圖1(b)為采用該算法對邊緣提取的結果。

圖1 Prewitt算子及縱向模板算法提取邊緣的結果

從仿真結果可以看出:與Prewitt算子相比，縱向模板算法對圖像中背景和目標對比度較小的部分邊緣提取較為完整，對于圖像中的輔道邊緣，算法未能完整提取。從整體效果上講，算法對機場下視景圖像邊緣的提取要優于Prewitt梯度算子。

為提高邊緣提取的速度，可以將模板尺寸放大，有下面的5×5縱向模板和7×7縱向模板，

采用這兩個模板提取圖像邊緣的算法原理與MZ3×3相同。

接著使用Matlab語言編程，為便于對照，仍然選擇某機場下視景圖像對提出的縱向5×5模板算法和縱向7×7模板算法進行仿真實驗。圖2(a)為265×351的某機場原始圖像，為便于對比，將縱向3×3模板算法結果置放于此，如圖2(b)所示。圖2(c)為采用縱向5×5模板算法對邊緣提取的結果，圖2(d)為采用縱向7×7模板算法對邊緣提取的結果。

圖2 縱向模板算法提取邊緣的結果

從仿真結果可以看出:3種模板對機場下視景圖像邊緣的提取均較為完整，整體效果相當，只是隨著模板尺度的增加，邊緣圖像稍有模糊。

下面，對這3種算法邊緣提取的時間開銷情況予以分析。圖3(a)中分別對3種縱向模板進行了10次隨機的耗時量統計，如橫軸所示，縱軸表示對應的開銷時間。

從圖3可以看出:縱向7×7模板算法耗時最少，10次耗時均值為0.53 s;縱向5×5模板算法次之，耗時均值為0.62 s;縱向3×3模板算法花費時間最長，耗時均值為1.00 s。即隨著縱向模板尺度的增大，提取圖像邊緣的時間減小。

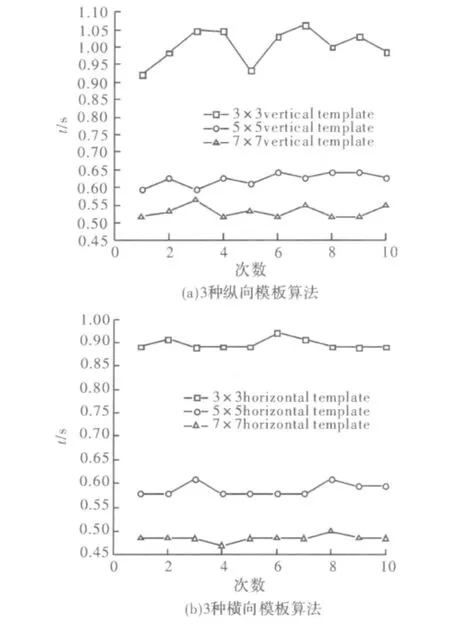
圖3 縱、橫向模板算法耗時比較

2 橫向模板算法

橫向模板算法中的“橫向”，是指模板在圖像上遍歷矩陣相乘后，得到的是圖像的橫向灰度差，即相鄰列之間的灰度差。

各種尺度的橫向模板如下所示

在縱向模板算法中，是以模板MZ左乘圖像G的，而在橫向模板算法中，Mh則是右乘圖像G的，

式(8)中“?”表示遍歷相乘，注意到結果矩陣的第n－1列和第n列中的各個對應元素絕對值相等且互為相反數，這是因為第n列是結果矩陣的最后一列，無法向后相減，便用向前相減替代之。用表示式(8)矩陣中的元素，其中1≤i≤m，時，將aij的灰度值置將aij的灰度值置為0，這樣就得到了采用橫向模板算法時圖像G的多像素二值邊緣圖。式中閾值M的選取方法與式(2)相同。

使用Matlab語言編程，對提出的橫向模板算法進行仿真實驗。為便于對比，將縱向3×3模板算法結果置放于此，如圖4(a)所示，圖4(b)為采用橫向3×3模板算法對邊緣提取的結果，圖4(c)為采用橫向5×5模板算法對邊緣提取的結果，圖4(d)為采用橫向7×7模板算法對邊緣提取的結果。

圖4 橫向模板算法提取邊緣的結果

由實驗結果可以看出:橫向3×3模板算法的邊緣提取效果優于縱向3×3模板算法。這一點可以由位于右側的斜向貫穿圖像上下的輔道看出，縱向模板算法幾乎未提取到該邊緣，而橫向模板算法對該邊緣提取得較為完整;橫向3種模板算法對機場邊緣提取效果相當，均較完整地檢測到了圖像邊緣。

下面，對這3種橫向模板算法邊緣提取的時間開銷情況進行分析。圖3(b)中分別對3種縱向模板進行了10次隨機的耗時量統計，如橫軸所示，縱軸表示對應的開銷時間。

從該圖可以看出:橫向7×7模板算法耗時最少，10次耗時均值為0.48 s;橫向5×5模板算法次之，耗時均值為0.59 s;橫向3×3模板算法花費時間最長，耗時均值為0.89 s。整體上，橫向模板算法的耗時量要小于縱向模板。這是因為該下視景機場圖像265×351的尺寸格式所致，其行數少于列數，故橫向時耗時少，縱向時耗時多。

由以上分析可知，無論是縱向模板算法還是橫向模板算法，其對下視景機場圖像邊緣的提取都要優于梯度算子，從耗時角度講，縱、橫向模板算法與Prewitt梯度算子相當。因此，對縱、橫向模板算法提出以下改進算法。

3 縱向和橫向模板算法的改進

在前述算法中，依據梯度算子模板的思路，提出了縱向和橫向模板算法的N×N，N=3，5，7模板，但注意到當采用縱向模板算法時，模板中的最后一行沒有起到算法目的，只是將原像素值再次賦給了當前像素點。同理，當采用橫向模板算法時，模板中的最后一列亦沒有起到算法目的［8］。

針對以上算法缺點，在縱向模板算法中可以將對算法沒有貢獻的最后一行去掉，這時，相應模板改變為

同理，在橫向模板算法中可以將對算法沒有貢獻的最后一列去掉，這時，相應模板改變為

對改進后算法進行仿真，結果顯示，邊緣提取效果與改進前幾乎沒有差別，所以在此不再列顯邊緣提取效果，但耗時情況有所改善，具體情況見圖5。圖5(a)是縱向模板算法改進前后的耗時情況對比，圖5(b)是橫向模板算法改進前后的耗時情況對比。

圖5 模板算法改進前后耗時比較

由圖5(a)可以看出，縱向7×7模板算法耗時最少，10次耗時均值為0.50 s;縱向5×5模板算法次之，耗時均值為0.6 s;縱向3×3模板算法花費時間最長，耗時均值為0.98 s;由圖5(b)可以看出，橫向7×7模板算法耗時最少，10次耗時均值為0.45 s;橫向5×5模板算法次之，耗時均值為0.57 s;橫向3×3模板算法花費時間最長，耗時均值為0.84 s，如表1所示。

表1 縱、橫向模板算法改進前后耗時對比

表1反映了模板算法改進前后的時間花費情況，對于縱向模板算法，改進后平均耗時減少了3.3%，橫向模板算法改進后平均耗時減少了4.6%。

4 結束語

提出了一種基于新模板提取圖像邊緣的方法，并基于該方法的實際機理，從提取圖像邊緣的耗時方面進行了有益改進。從實驗結果得到以下結論:(1)利用縱、橫模板提取圖像邊緣的方法，采用Matlab語言編程對1幅265×351大小的圖像進行邊緣提取時，效果要優于Prewitt算法，且耗時與其相當，僅為0.48～0.53 s。(2)針對邊緣提取的時間優化，對縱、橫模板提取圖像邊緣的方法進行了改進，在保證提取圖像邊緣信息幾乎不變的情況下，將縱、橫模板提取圖像邊緣的時間分別減少了3.3%和4.6%。(3)提出的縱、橫模板提取圖像邊緣的方法，具有模型簡單且實時性強等特點。對于圖像邊緣實時提取領域的開發和研究，以及利用該算法對圖像定位與匹配等領域進一步的研究，具有一定意義。

［1］ BEHZAD K P，BEHROOZ K P，AZRIEL R．Optimally isotropic laplacian operator［J］．IEEE Transactions on Image Processing，1999，8(10):1467－1472．

［2］ MEJJAOLI H，TRIMECHE K．On a mean value property associated with the dunkl laplacian operator andapplications［J］．Integral Transforms and Special Functions，2001，12(3):279－302．

［3］ 劉煜．飛行器下視景像預處理及實時匹配技術研究［D］．西安:西北工業大學，2007．

［4］ 梁光明，孫即祥，馬琦，等．Ostu算法在Canny算子中的應用［J］．國防科技大學學報，2003，25(5):36－39．

［5］ 岳振軍，邱望成，劉春林．一種自適應的多目標圖像分割方法［J］．中國圖象圖形學報:A輯，2004，9(6):674－678．

［6］ 杜健輝，呂文閣，侯夢華．基于競選算法的Otsu閾值快速確定方法［J］．機電工程技術，2007，36(3):57－58．

［7］ 任繼軍．基于灰度空間自動閾值選取的彩色舌圖像分割算法［J］．陜西科技大學學報:自然科學版，2005，23(2):73－77．

［8］ 劉煜，李言俊，張科．一種多像素圖像邊緣提取方法［J］．光子學報，2007，36(2):380－383．