基于空間信息的FCM醫(yī)學(xué)圖像高效分割

王黎明

(西安電子科技大學(xué)電子工程學(xué)院，陜西西安710071)

醫(yī)學(xué)圖像分割是醫(yī)學(xué)圖像分析和處理的關(guān)鍵技術(shù)［1－3］，它是醫(yī)學(xué)圖像處理中重要內(nèi)容之一，是實(shí)現(xiàn)圖像測(cè)量、配準(zhǔn)、融合以及三維重建的基礎(chǔ)，在臨床診斷中發(fā)揮著越來(lái)越重要的作用，分割的準(zhǔn)確性直接影響后續(xù)任務(wù)的有效性。所謂醫(yī)學(xué)圖像分割就是指將醫(yī)學(xué)圖像分解成互不相交的不同空間區(qū)域，使得每個(gè)區(qū)域的像素具有相似的特征，而不同區(qū)域內(nèi)的像素間存在特征差異，以便把感興趣的區(qū)域從復(fù)雜的背景中分離出來(lái)。

醫(yī)學(xué)圖像本質(zhì)上是模糊的，在醫(yī)學(xué)圖像中存在許多不確定性的因素，如灰度、紋理和區(qū)域的邊界等。雖然這些不確定性給圖像分割帶來(lái)了許多困難，但卻給模糊聚類分析提供了用武之地。模糊聚類是非監(jiān)督模式識(shí)別的主要技術(shù)之一［4－5］，應(yīng)用時(shí)可以減少人為干預(yù)，非常適合于灰度圖像中存在不確定性和模糊性的特點(diǎn)。在模糊聚類方法中，F(xiàn)CM(Fuzzy c－means)算法是最流行的方法，因?yàn)樗鼘?duì)模糊特征具有很強(qiáng)的魯棒性，而且相比硬分割能保留更多的信息。雖然傳統(tǒng)的FCM算法在無(wú)噪聲或噪聲很低的圖像分割中能得到較好的分割效果，但由于它只考慮了圖像像素的灰度信息，未利用圖像像素的空間信息，從而使得該算法對(duì)噪聲很敏感。

近年來(lái)很多研究者在考慮像素空間信息的前提下，通過(guò)修改標(biāo)準(zhǔn)FCM聚類算法的目標(biāo)函數(shù)或者隸屬度函數(shù)使得圖像分割的性能得到提高［6－9］。文獻(xiàn)［6］通過(guò)引入一個(gè)中值濾波圖像對(duì)標(biāo)準(zhǔn)FCM算法的目標(biāo)函數(shù)進(jìn)行修改，修改后的FCM算法，KFCM_S2，提高了在分割帶有噪聲圖像時(shí)的性能，并已成功應(yīng)用到MRI數(shù)據(jù)的分割中。文中算法mFCM(modified Fuzzy CMeans)在此基礎(chǔ)上加入模糊空間信息，即引入表征鄰域像素對(duì)當(dāng)前像素作用的先驗(yàn)概率來(lái)重新確定當(dāng)前像素的模糊隸屬度值，使圖像在噪聲下的分割性能大大提高，先驗(yàn)概率自動(dòng)取決于算法執(zhí)行中的模糊隸屬度，同時(shí)進(jìn)一步調(diào)整距離矩陣，引入距離空間信息。該算法中用一個(gè)標(biāo)準(zhǔn)FCM算法的直方圖初始化，收斂速度大大提高。試驗(yàn)結(jié)果表明，該算法相當(dāng)有效，對(duì)噪聲具有很強(qiáng)的抑制能力。

1 標(biāo)準(zhǔn)FCM

由Bezdek等人提出的標(biāo)準(zhǔn)FCM［10］聚類算法是從硬C－均值算法發(fā)展而來(lái)，其基本思想是通過(guò)迭代尋找最優(yōu)聚類中心vi和隸屬度函數(shù)uik，使得目標(biāo)函數(shù)

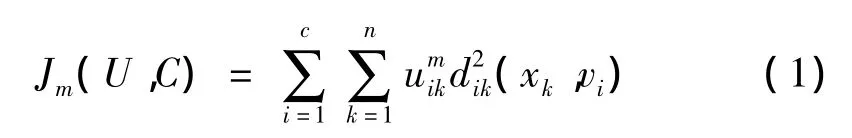
達(dá)到最小，以實(shí)現(xiàn)圖像的優(yōu)化分割。

數(shù)據(jù)集X(x1，x2，…，xn)∈Rpn為圖像灰度值的集合;p為樣本xk，k=1，2，3，…，n的維數(shù);c為預(yù)定的聚類數(shù)目;uik表示X中任意樣本xk屬于聚類i的隸屬度函數(shù);vi，i=1，2，…，c為每個(gè)聚類的聚類中心;2≤c≤n，m∈［1，∞)為聚類加權(quán)指數(shù)，它控制數(shù)據(jù)劃分過(guò)程的模糊程度，當(dāng)m=1時(shí)，模糊聚類就退化為硬C均值聚類。研究表明，m=2是比較理想的取值;d2ik(xk，vi)為第k個(gè)像素到第i類聚類中心的距離，這里取歐幾里得距離。

顯然，標(biāo)準(zhǔn)FCM只考慮了圖像的灰度信息，而沒(méi)有考慮圖像的空間信息。

2 直方圖初始化

標(biāo)準(zhǔn)FCM分割圖像時(shí)，由于圖像數(shù)據(jù)量一般比較大，因此算法收斂將花費(fèi)很長(zhǎng)時(shí)間。文中給出一種快速FCM方法，利用直方圖初始化，將圖像從像素空間映射到其灰度直方圖特征空間，從而使算法的速度大大提高。

基于模糊聚類的直方圖優(yōu)化函數(shù)如下

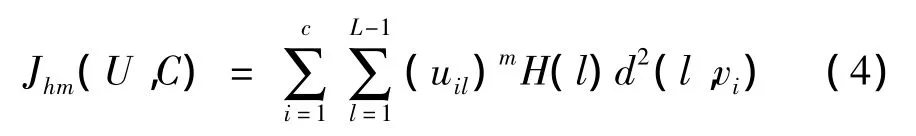
式中，H是L灰度級(jí)圖像的直方圖，H(l)為具有灰度級(jí)l的像素個(gè)數(shù)，所有像素的灰度值取值為{0，1，…，L－1}，這樣隸屬度的計(jì)算就化簡(jiǎn)為以l為灰度值的一個(gè)像素的隸屬度。

由L層灰度級(jí)隸屬函數(shù)約束條件

最小化上述目標(biāo)函數(shù)，從而得到隸屬函數(shù)uil和基于FCM直方圖的聚類中心vi

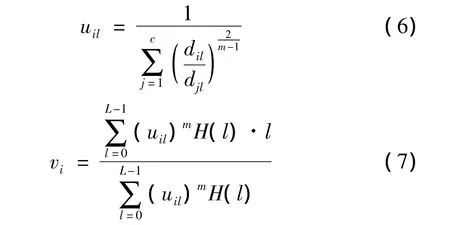
設(shè)圖像的大小為256×256，灰度級(jí)Lmax=256，則此算法速度提高256×256/256=256倍，即通過(guò)引入直方圖初始化，將所有像素的隸屬度和聚類中心的計(jì)算轉(zhuǎn)化為256個(gè)灰度值的隸屬度和聚類中心的計(jì)算，算法執(zhí)行速度大大提高。但實(shí)驗(yàn)表明，其分割的效果和標(biāo)準(zhǔn)FCM的分割效果一樣。

3 mFCM算法

根據(jù)馬爾可夫隨機(jī)場(chǎng)MRF(Markov Random Field)理論，圖像中絕大多數(shù)像素和它鄰近的像素一樣屬于同一聚類。空間信息加入到標(biāo)準(zhǔn)FCM中，使得算法對(duì)噪聲和模糊的邊緣具有很強(qiáng)的魯棒性。本文在文獻(xiàn)［6］的基礎(chǔ)上修改隸屬度函數(shù)，加入鄰域模糊空間信息，從而提高對(duì)噪聲的魯棒性。

mFCM算法的目標(biāo)函數(shù)為

其對(duì)應(yīng)的改進(jìn)模糊隸屬度和聚類中心迭代函數(shù)為

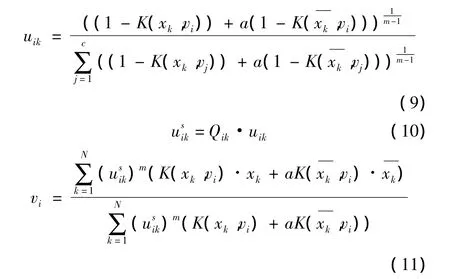
其中，Qik是先驗(yàn)概率，即第k像素屬于第i聚類的概率。文中給出一種簡(jiǎn)單且易實(shí)現(xiàn)的計(jì)算方法，即

式中，Nk是xk鄰域的像素總數(shù)目，可任意給定;是去模糊化后xk鄰域像素中屬于聚類i的像素?cái)?shù)目，初始值的確定是在直方圖初始化后，根據(jù)最大隸屬度原則將其鄰域像素歸結(jié)到隸屬度最大的一類中，統(tǒng)計(jì)出鄰域中屬于每一類的總數(shù)目。

本算法加入的模糊空間信息是式(10)中的第一項(xiàng)，表征鄰域像素對(duì)當(dāng)前像素作用的先驗(yàn)概率來(lái)重新確定當(dāng)前像素的模糊隸屬度值，先驗(yàn)概率自動(dòng)取決于算法執(zhí)行中的模糊隸屬度，因此當(dāng)某像素的鄰域像素隸屬于某聚類的數(shù)目越多時(shí)，該像素隸屬于此聚類的概率就越大。

上述算法執(zhí)行過(guò)程中對(duì)隸屬度函數(shù)的改進(jìn)，進(jìn)一步增強(qiáng)了分割圖像時(shí)對(duì)噪聲的魯棒性，為更好地消除噪聲的影響，取得更理想的分割圖像，考慮在算法的計(jì)算過(guò)程中對(duì)核距離矩陣進(jìn)行改進(jìn)。Kik的含義是像素k到第i類的核距離，接下來(lái)引入核距離空間信息，在每一次迭代過(guò)程中，都要對(duì)Kik進(jìn)行一次調(diào)整。例如對(duì)于任意像素k屬于第一類，先把K1k調(diào)整成與圖像具有相同大小的矩陣形式K1，這對(duì)于核距離矩陣K1便出現(xiàn)了鄰域信息，然后把任意元素K1k和它的鄰域元素求平均值K'1k，用K'1k來(lái)代替K1k，這樣就可以進(jìn)一步減少噪聲點(diǎn)的影響。用相同的方法對(duì)所有像素和各類所形成的核距離矩陣進(jìn)行處理，得到一個(gè)新的核距離矩陣K'ik。

算法的具體實(shí)現(xiàn)為:

(1)給定ε、c和Nk后，利用直方圖初始化對(duì)圖像進(jìn)行初始分割，根據(jù)式(6)和式(7)計(jì)算出收斂后的聚類中心做為算法的初始聚類中心，并根據(jù)收斂后的隸屬度計(jì)算出初始先驗(yàn)概率。

(2)根據(jù)式(9)～式(11)計(jì)算出新的隸屬度和聚類中心。

(3)判斷算法是否收斂，如果不收斂，則將所得的隸屬度做為初始化隸屬度，重新計(jì)算先驗(yàn)概率并轉(zhuǎn)到(2)，否則轉(zhuǎn)到(4)。

(4)根據(jù)隸屬度矩陣，利用最大隸屬度原則，將軟分割結(jié)果轉(zhuǎn)化為硬分割結(jié)果，輸出分割結(jié)果，算法結(jié)束。

由于該方法利用直方圖初始化，因此算法的收斂速度很快，且不易陷入局部最小點(diǎn)。

4 實(shí)驗(yàn)結(jié)果與分析

為驗(yàn)證本算法的高效性和對(duì)噪聲的魯棒性，用標(biāo)準(zhǔn)測(cè)試圖像Lena和MRI腦部真實(shí)醫(yī)學(xué)圖像做了實(shí)驗(yàn)，并且分別對(duì)比了傳統(tǒng)的FCM和KFCM_S2的分割效果。算法中的參數(shù)設(shè)置分別為:ε=1.0e－6，m=2，Nk=8。由于算法的開(kāi)始利用直方圖初始化，初始化后算法經(jīng)過(guò)幾次迭代就迅速收斂，具有較強(qiáng)的實(shí)時(shí)性。

實(shí)驗(yàn)1標(biāo)準(zhǔn)測(cè)試圖像Lena，分別利用傳統(tǒng)的FCM，KFCM_S2與文中mFCM算法分割進(jìn)行比較，類別數(shù)為4。從圖1～圖4可以看出，本文改進(jìn)的算法具有較強(qiáng)的抑制噪聲的能力。為定量地評(píng)估這3種方法的性能，文中采用文獻(xiàn)［11］給出的區(qū)域非一致性函數(shù)準(zhǔn)則進(jìn)行比較，該函數(shù)的表達(dá)式為

式中，NU是區(qū)域的非一致性測(cè)度;FT和BT分別代表前景和背景的像素;是指集合的基數(shù);σ2f是前景的方差;σ2是整幅圖像的方差。根據(jù)文獻(xiàn)［12］的說(shuō)明，如果越小則表示分割的結(jié)果越好，其值越大則分割的結(jié)果越差。根據(jù)這一準(zhǔn)則函數(shù)的定義，3種算法的計(jì)算結(jié)果如表1所示，由表可見(jiàn)，本文mFCM算法得到的NU小于傳統(tǒng)FCM和KFCM_S2算法，即mFCM算法相對(duì)于這兩種方法，分割效果好。

表13 種算法的NU計(jì)算

實(shí)驗(yàn)2用MRI腦部真實(shí)醫(yī)學(xué)圖像測(cè)試在不同噪聲水平下，mFCM算法的分割效果。類別數(shù)為2，椒鹽噪聲的含量分別為3%、5%、7%和9%。圖5～圖10給出了在不同噪聲水平下，本文算法的分割結(jié)果。容易看出，隨著噪聲級(jí)數(shù)的增加，mFCM算法還能有效地分割圖像，可見(jiàn)，與KFCM_S2算法相比，本文算法在克服噪聲對(duì)分割結(jié)果的影響方面表現(xiàn)出較強(qiáng)的魯棒性和優(yōu)越性。

圖7 疊加3%噪聲圖像下，KFCM_S2，mFCM算法的分割結(jié)果對(duì)比

5 結(jié)束語(yǔ)

提出在KFCM_S2的基礎(chǔ)上引入模糊空間信息，即在原隸屬度函數(shù)的基礎(chǔ)上，加入表征像素對(duì)當(dāng)前像素作用的先驗(yàn)概率重新確定當(dāng)前像素的隸屬度函數(shù)，同時(shí)修改距離矩陣，引入距離空間信息，從而合理利用了空間信息。算法的開(kāi)始對(duì)圖像直方圖初始化，使得算法的收斂速度得到提高。實(shí)驗(yàn)結(jié)果表明，該改進(jìn)算法在去除噪聲和提高分割精確度方面，有明顯改進(jìn)，是一種穩(wěn)健高效的醫(yī)學(xué)圖像分割方法。

［1］ LIN Y，TIAN J．A survey on medical image segmentation methods［J］．Pattern Recognition and Artificial Intelligence，2002，15(2):192－204．

［2］ PAL N R，PAL S K．A review on image segmentation techniques［J］．Pattern Recognition，1993，26(9):1277－1294．

［3］ PHARN D L，XU C Y，PRINCE J L．A survey of current methods in medical image segmentation［R］．Technical Report JHU/ECE99－01，Johns Hopkins University，1998．

［4］ FRANCESCO M，ANDREA S．A fuzzy clustering based segmentation system as support diagnosis in medical imaging［J］．Artif Intel in Med，1999，16(2):129－147．

［5］ 聶生東，陳瑛，顧順德，等．磁共振顱腦圖像快速模糊聚類分割算法的研究［J］．中國(guó)生物醫(yī)學(xué)工程學(xué)報(bào)，2001，20(2):104－109．

［6］ CHEN S C，ZHANG D Q．Robust image segmentation using fcm with spatial constraints based on new kernel－induced distance measure［J］．IEEE Trans．Systems Man Cybernet，B，2004，34(4):1907－1916．

［7］ AHMEND M N，YAMANY S M，MOHAMED N．A modified fuzzy c－means algorithm for bias field estimation and segmentation of MRI data［J］．IEEE Trans．on Medical Imaging，2002，(21):193－199．

［8］ CHUANG K S，TZENG H L，CHEN S W．Fuzzy C－means clustering with spatial information for image segmentation［J］．Computerized Medical Imaging and Graphic，2006(30):9－15．

［9］ Zhang D Q，Chen S C，Pan Z S．Kernel－based fuzzy clustering incorporating spatial constraints for image segmentation［C］．Proc．International Conference on Machine Learning and Cybennetics，2003(4):2189－2192．

［10］ BEZDEK J C，PAL S K．Fuzzy models for pattern recognition［M］．Piscataway，NJ，USA:IEEE Press，1999．

［11］ SEZGIN M，SANKUR B．Survey over image thresholding techniques and quantitative performance evaluation［J］．Journal of Electronic Imaging，2004，13(1):146－165．

［12］ COLLINS D L，ZIJDENBOS A P，KOLLOKIAN V．Design and construction of a realistic digital brain phantom［J］．IEEE Trans Med Imag，1998，17(3):463－468．