9自由度混聯(lián)微創(chuàng)外科機器人的正反解

張 帆 劉 達 王田苗

(北京航空航天大學 機械工程及自動化學院,北京 100191)

9自由度混聯(lián)微創(chuàng)外科機器人的正反解

張 帆 劉 達 王田苗

(北京航空航天大學 機械工程及自動化學院,北京 100191)

針對北京航空航天大學機器人研究所最新開發(fā)的用于胸腹部冷凍穿刺手術的 9自由度“5R+4T”混聯(lián)機器人,基于指數(shù)積公式,利用反變換法和逆矩陣的特性,提出了一種在單約束條件下,得到該機器人解析形式正反解的新算法.通過數(shù)值算例驗證了正反解的互推性,即算法的有效性,并經(jīng)過對算例的分析給出了修正方案,擴大了算法的適用范圍.該方法克服了因為混聯(lián)機器人自由度多、結構復雜而帶來的難以完成正反解計算的困難,為多自由度混聯(lián)機器人的運動學求解提供了一種新的思路.

微創(chuàng)外科;混聯(lián)機器人;正反解;指數(shù)積

機器人的正解與反解計算作為一對互逆的過程是機器人運動學研究中最基本的問題.諸如工作空間的計算與描述、靈活性和剛度的評價以及機器人的實時控制和軌跡規(guī)劃等研究工作都以其為基礎.常見求解方法有很多,如經(jīng)典的“D-H”法[1],基于指數(shù)積的子問題法[2]以及其他基于旋量的方法等.然而,使用上述方法的研究基本都以常規(guī)的串聯(lián)機器人或并聯(lián)機器人為對象[3-5],對于多自由度混聯(lián)機器人的整體運動學建模的相關研究報道甚少.

本文所做的工作是針對北京航空航天大學機器人研究所最新開發(fā)的用于胸腹外科冷凍穿刺手術的“5R+4T”(R指旋轉關節(jié),T指移動關節(jié))9自由度混聯(lián)機器人進行的.傳統(tǒng)的分析方法如“D-H”法,因為初始坐標系設置的復雜性,以及由此帶來的計算可行性的下降使其并不適用于混聯(lián)機器人的運動學求解.文獻[6]對該機器人做過運動學的分析,但其方法對機器人拓撲結構有較大的簡化,而且只得到了數(shù)值解.本文基于指數(shù)積公式,利用反變換法和逆矩陣的特性,得出了單約束條件下此種 9自由度混聯(lián)機器人的解析形式正反解,即封閉解,并通過正反解的互推,驗證了其正確性.研究結果為將來的全主動關節(jié)形式下,機器人的位置控制提供了必要的理論前提和基礎.

1 機器人本體介紹

如圖 1所示,混聯(lián)機器人由一個“5R”的串聯(lián)機械臂和其末端夾持的一個“4T”的并聯(lián)平臺組成.

圖 1 混聯(lián)微創(chuàng)外科穿刺機器人

其主要功能是在 CT(Computed Tomography)圖像的導引下,根據(jù)醫(yī)生的要求,實現(xiàn)穿刺針的空間定位.串聯(lián)臂的各個關節(jié)可通過一個踏板控制,經(jīng)由其內部液壓力來鎖緊或松開,其功能是在較大的范圍內進行粗定位.并聯(lián)平臺由結構完全一樣的上下兩層組成,每一層都類似于一個 x-y工作平臺,具有兩個方向相互垂直的移動自由度,能夠分別使其上的球鉸在該層所在平面內運動,從而實現(xiàn)小范圍內的精確定位.上下兩個球鉸的中心可以確定一個空間矢量,即:穿刺針的進針矢量.醫(yī)生在由兩個球鉸組成的滑道的導引下,沿著進針矢量將穿刺針推入病人體內,完成穿刺過程.

2 運動學正解

對于“5R+4T”的混聯(lián)機構,運動學正解是指:在已知全部 9個關節(jié)的關節(jié)變量的情況下,求出穿刺針針尖點的位置坐標.為解決這一問題,可將串聯(lián)部分與并聯(lián)平臺的上下兩層分別組合,組成兩個形式相同的“5R+2T”串聯(lián)分支,分別稱為上分支和下分支,如圖 2所示.

圖 2 混聯(lián)機器人結構

2個分支的前 5個關節(jié)(即串聯(lián)臂)是共用的,擁有相同的關節(jié)變量.通過各自所擁有的 7個運動副,兩個分支分別能確定一個球鉸點的空間位置.同時,設定穿刺針沿兩個球鉸所定的方向進針并完成穿刺后,其尾端與上分支的球鉸中心重合,而針尖與目標點重合,即:在機器人的最終位形下,上球鉸中心與目標點之間的距離等于穿刺針的長度.至此,整個混聯(lián)機構的正向運動學解算就集中轉化為求解上、下分支的運動學正解.

而指數(shù)積公式在求解串聯(lián)結構的正向運動學時具有很大的便利性.通過對每個關節(jié)軸定義一個單位運動旋量 ξ,可以在只設定基坐標系和末端的工具坐標系兩個坐標系的前提下,利用所有關節(jié)單位運動旋量的連乘積表示出上述兩個坐標系的相對位置關系,從而求得正解[7].

取圖 2中所示位形為初始位形,建立基坐標系和工具坐標系.上述兩圖中的工具坐標系實際分別都建立在上下分支的球鉸中心處,但因為不考慮移動副的機械結構限制,認為初始時球鉸中心能經(jīng)由兩個移動關節(jié)收回到并聯(lián)平臺的角點處,故工具坐標系位于圖 2中所示的 C點和D點.

初始位形時,上下兩個分支的工具坐標系相對于基坐標系的變換矩陣分別為

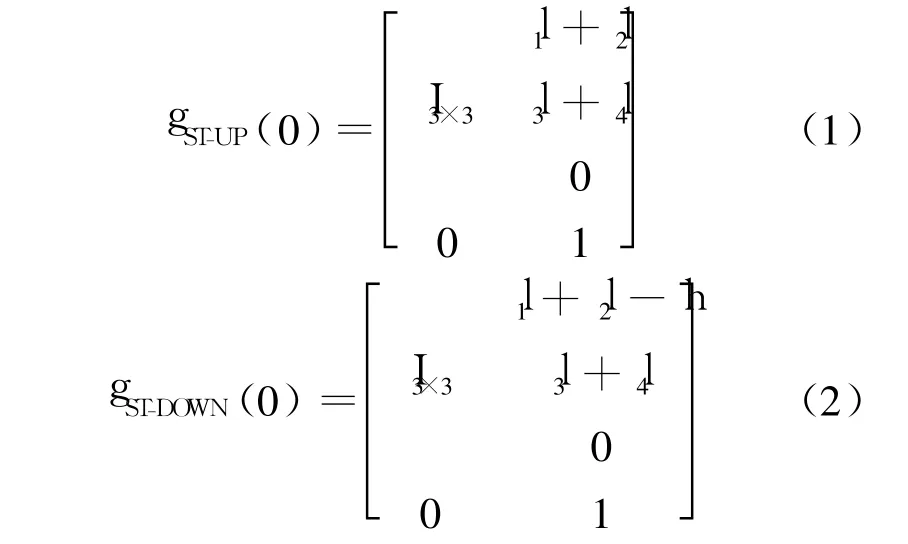
式中,I3×3表示 3階的單位矩陣;l1,l2,l3,l4和 h均為結構參數(shù).

圖 2中 9個關節(jié)的單位運動旋量 ξ1～ξ7,ξ66和 ξ77計算如下:

考慮到

則

根據(jù)指數(shù)積公式,上分支的工具坐標系相對于基坐標系的變換矩陣可以表示為

該矩陣第 4列的前 3行即為上分支球鉸中心點 S1的坐標(x1,y1,z1)T.

同理,下分支的工具坐標系相對于基坐標系的變換矩陣為

該矩陣第 4列的前 3行即為下分支球鉸中心點 S2的坐標(x2,y2,z2)T.

此時,穿刺針的方向矢量即為

令(cosα,cosβ,cosγ)為穿刺針矢量的方向余弦,則

令 L為穿刺針的長度,即平臺上平面球鉸中心點S1到穿刺針針尖點 E的距離,則E點的坐標為

通過以上正解的過程,可以看出,在對混聯(lián)機器人拓撲結構進行合理的分拆后,其正解的特點類似于傳統(tǒng)串聯(lián)機器人的正解,相對比較簡單,也能充分發(fā)揮出指數(shù)積公式初始坐標系設置簡單的優(yōu)越性.

3 單約束條件下的反解

反解的過程是首先經(jīng)由穿刺針末端點的坐標和針的長度及姿態(tài)矢量回推出上平臺球鉸中心點S1的坐標,再根據(jù)手術需要給出并聯(lián)平臺上的工具坐標系的姿態(tài)矩陣 R(θ).以這兩個條件作為反解初始條件,首先對上分支 7自由度串聯(lián)結構進行附加約束條件的解算,得到 θ1～θ7的值.再根據(jù)已求出的 θ1～θ5,利用逆矩陣的特性,解出下分支中的 θ66和 θ77,從而完成全部 9個關節(jié)的反解.

3.1 反解初始條件

已知穿刺針末端點 E(xE,yE,zE),穿刺針長度 L,穿刺針姿態(tài)(α,β,γ),以及 3階的并聯(lián)平臺姿態(tài)矩陣 R(θ),則平臺上平面球鉸中心點 S1的坐標即為

根據(jù)由點 S1的坐標和 R(θ)構成的gST-UP(θ)可以對由 7個運動副串聯(lián)而成的上分支進行運動學反解,進而得到 7個關節(jié)變量 θ1～θ7的值.

3.2 上分支反解

根據(jù)實際操作經(jīng)驗,串聯(lián)臂的第 4關節(jié)在實際手術中很少需要做大幅度轉動,經(jīng)常處于相對固定的位置.因此,本文將 θ4角固定,這樣的簡化使得在實際手術需要仍能得到滿足的前提下,算法的可解性大為改觀.此即為約束條件.

式(14)兩端的元素(3,1)對應相等,可以得到以下的關系式:

式中,±號對應于 θ1的兩個可能解.選定 θ1的解之后,再令式(14)兩端的元素(1,1)和(2,1)分別對應相等,可得只要 c4≠0,便可求出

當 c4=0時,操作臂處于奇異形位.此時,關節(jié)軸 2,3和 5平行,只能解出 θ2+θ3與 θ5的差.奇異位形可由式(18)中 arctan2的兩個變量是否都接近 0來判斷.若都接近 0,則為奇異形位,否則不是奇異形位.在奇異形位時,可任意選取θ2+θ3的值,再計算相應的 θ5值.

式(19)兩邊元素(2,2)和(3,2)分別對應相等,得

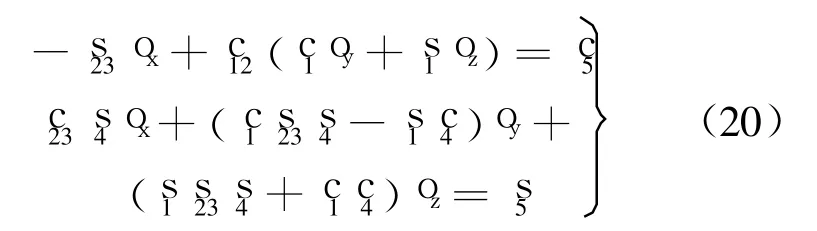
由此得到 θ5的解:

再令式(14)兩邊元素(1,4),(2,4)和(3,4)分別對應相等,可得如下方程組:

對式(22)中的已知量進行移項合并,并做代換處理,可得

通過式(23)中 3個方程彼此間的線性運算,可以將 θ6和 θ7消去.再對已知量做代換處理,進而能夠得到:

式中,A1～A9,B1～B3均為由已知量組成的代數(shù)式.

觀察式(24)的形式,與式(15)相同.所以可以采用求解 θ1的方法來求解 θ2.同樣,θ2有兩個解 ,在選定 θ2的值后,根據(jù)式 (18),θ3的解即為

上述矩陣方程兩邊元素(2,4)和(3,4)分別對應相等,可得 θ6和 θ7.因其結果一目了然,在此不再贅述.

3.3 下分支反解

如圖 3,只考慮包括前 5個旋轉關節(jié)在內的串聯(lián)部分,設置末端坐標系 T和基坐標系.初始位形時,末端坐標系相對于基座標系的變換矩陣為

因此,根據(jù)指數(shù)積公式,末端坐標系相對于基坐標系的變換矩陣為

又因為,對于

有

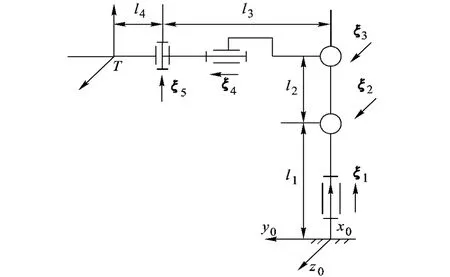
圖 3 串聯(lián)機械臂結構

根據(jù)式(30),可以求出基坐標系相對于末端坐標系的變換矩陣 g-1ST(θ),進而可以將已知的 E點和 S1點在基坐標系下的坐標表示變換為在末端坐標系 T下的表示,即

式中,E,TE,S1和TS1均為齊次坐標表示.

在末端坐標系 T下,令

則穿刺針所在直線的方程為

又,并聯(lián)平臺下層所在的平面可表示為

將式(33)和式(34)聯(lián)立,可解出下分支球鉸中心點 S2的坐標 (在末端坐標系 T下的表示),即

從而,可得到下分支兩個移動副的關節(jié)變量的值,即

至此,θ1～ θ7,θ66,θ77全部 9個關節(jié)變量均得解,運動學反解完成.

由式(16)可知,在分別取正號或負號時,θ1有兩組解,而 θ2亦如此.根據(jù)排列組合原理,在本文提出的算法下,任一個可達的末端位姿經(jīng)由反解,將對應 4組可能的關節(jié)變量值.若不考慮各關節(jié)機械結構的限制,僅從數(shù)學角度來看,這 4組解都應該是正確的.

4 數(shù)值驗證

針對以上所述的正反向運動學的求解,通過Matlab編程,進行了驗證.具體采用的是一種雖然傳統(tǒng)但卻十分有效的方法,即:先為各個運動關節(jié)任取相應的關節(jié)變量值,進行正向求解;再利用正解的結果,代入反解的算法中,求出各個關節(jié)變量;然后對一開始任取的各關節(jié)變量和經(jīng)過反解求出的各關節(jié)變量進行比較,如果二者相同,則可說明算法本身的自洽性和有效性.

考慮各個關節(jié)的最大行程,任意給定 9個關節(jié)變量的值,如表 1中的第Ⅰ組數(shù)據(jù)所示.經(jīng)過先正解再反解的運算,得到包括其本身在內的 4組反解值,見表 1.

由表 1中的運算結果可以看出,只有當 θ1和θ2的求解公式都取正號時,正反解的互推關系才能成立.

表 2中,任選了 5組關節(jié)變量值,對混聯(lián)機器人正反解算法的互推性進行驗證.經(jīng)過運算,1～3組可以很順利地完成互推,而第 4組和第 5組則代表不同于前 3組的比較特殊的一類.這兩組值在選定 θ1和 θ2求解公式的正負號后,經(jīng)解算得出的 9個值中,會出現(xiàn) θ2的異常突變,表現(xiàn)為絕對值過大,以至于接近 2π,并間接導致 θ3計算結果的錯誤.但與此同時,θ2+θ3和其余 7個關節(jié)變量的結果卻都是正確的.這主要是由 θ2求解公式本身的復雜性,及三角函數(shù)以 2π為周期的特性共同作用而導致的.對于第 4組數(shù)據(jù),會得到一個絕對值較大的負值;而第 5組數(shù)據(jù),則會得到一個絕對值較大的正值.要想解決這個問題,只需要給這兩個異常的 θ2分別加上和減去一個 2π便可以得到正確結果.因此,在實際運算時,就需要對本文提出的算法設置一個修正環(huán)節(jié).當經(jīng)過原算法計算后,若發(fā)現(xiàn) θ2的值異常偏大,就減去一個2π;反之,則加上一個 2π.

表 1 4組反解值

表 2 5組驗證用數(shù)據(jù)

5 結 論

綜上所述,本文基于指數(shù)積公式,利用反變換法和逆矩陣的特性,建立了本文中所研究的 9自由度混聯(lián)機器人的正反解算法,得到了單約束條件下的封閉解.該過程具有類似于求解串聯(lián)機器人運動學的特點,即:反解較難,正解相對簡單.通過數(shù)值算例,證明了算法的有效性,并提出了修正方案.

References)

[1]熊有倫,唐立新,丁漢,等.機器人技術基礎[M].武漢:華中科技大學出版社,1996 Xiong Youlun,Tang Lixin,Ding Han,et al.Fundamentals of robotics[M].Wuhan:Huazhong University of Science and Technology Press,1996(in Chinese)

[2]理查德·摩雷,李澤湘,夏恩卡·薩思特里.機器人操作的數(shù)學導論[M].北京:機械工業(yè)出版社,1998 Murray R M,Li Zexiang,Sastry S S.Amathematical introduction to robotic manipulation[M].Beijing:China Machine Press,1998(in Chinese)

[3]Jin Yan,Chen I-Ming,Yang Guilin.Kinematics analysis of a 6-DOF selectively actuated parallel manipulator[C]//Proceedings of the 2004 IEEE Conference on Robotics,Automation and Mechatronics.Singapore:IEEE,2004,1:231-236

[4]趙杰,劉玉斌,蔡鶴皋.一種運動旋量逆解子問題的求解及其應用[J].機器人,2005,27(2):163-167 Zhao Jie,Liu Yubin,Cai Hegao.Solution for one type of inverse kinematics sub-problem in screw theory and its application[J].Robot,2005,27(2):163-167(in Chinese)

[5]錢東海,王新峰,趙偉,等.基于旋量理論和 Paden-Kahan子問題的 6自由度機器人逆解算法[J].機械工程學報,2009,45(9):72-76 Qian Donghai,Wang Xinfeng,Zhao Wei,et al.An algorithm for the inverse kinematics calculation of 6-DOF robots based on screw theory and Paden-Kahan sub-problems[J].Journal of Mechanical Engineering,2009,45(9):72-76(in Chinese)

[6]Tang Can,Liu Da,Wang Tianmiao,et al.The kinematics modeling based on spinor theory for CT-guided hybrid robot[J].High Technology Letters,2009,15(1):20-25

[7]Brockett RW.Robotic manipulators and the product of exponentials formula[C]//Fuhrman P A.Mathematical Theory of Networks and Systems.Berlin:Springer-Verlag,1984:120-129

(編 輯:趙海容)

Forward and inverse solution of a 9-DOF hybrid robot for minimally invasive surgery

Zhang Fan Liu Da Wang Tianmiao

(School of Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Focusing on the recently developed“5R+4T” 9-DOF(degree-of-freedom)hybrid robot for thoracoabdominal percutaneous cryosurgery by the robotics institute of Beijing University of Aeronautics and Astronautics,an original single-constraint-condition algorithm was put forward to obtain analytic solutions to the forward and inverse kinematics of the robot,based on the productof exponentials(POE)formula using inverse transformationmethod and characteristics of inversematrix.Themutual derivation between the forward and the inverse solution,namely,the effectiveness of the algorithm,was demonstrated by several sets of numeric data.Amodification for the algorithm was also advanced by discussing the demonstration results,so as to expand the range of its applicability.This algorithm overcomes the difficulties in performing the forward and inverse kinematic calculations which result from the DOF redundancy and the structure complexity of the hybrid robot,bringing a new idea about solving kinematic problems of multi-DOF hybrid robots.

minimally invasive surgery;hybrid robot;forward and inverse solutions;product of exponentials(POE)

TP 242

A

1001-5965(2011)04-0446-06

2010-01-26

科技部國際合作資助項目(2006DFA 12290)

張 帆(1983-),男,河北石家莊人,碩士生,kurtgre@gmail.com.