力限振動試驗條件設計方法

莫昌瑜 袁宏杰

(北京航空航天大學 可靠性與系統工程學院,北京 100191)

力限振動試驗條件設計方法

莫昌瑜 袁宏杰

(北京航空航天大學 可靠性與系統工程學院,北京 100191)

給出了一種基于復雜二自由度模型的力限振動試驗條件設計方法.該方法應用動態子結構法計算試驗件結構和支持結構的模態有效質量和剩余質量,根據模態有效質量在頻域上的分布情況確定不同頻帶內振動系統的復雜二自由度模型參數,結合支持結構激勵條件給出試驗件與支持結構接觸面的力譜和加速度譜,在此基礎上進行包絡,得到力限振動試驗剖面.仿真結果表明,由該方法給出的力限振動試驗條件,與傳統加速度試驗條件相比,能更加真實地反應試驗件的振動環境.

復雜二自由度;力限;模態有效質量

航天器在發射的過程中要經受噪聲、振動和沖擊等力學環境的考驗,為保證航天器的安全性和可靠性,航天器在研制過程中需要進行充分的力學環境試驗.對于傳統加速度控制振動試驗而言,由于試驗條件制定得過于保守,導致振動臺難以正確地復現航天器真實的力學環境,容易造成過試驗.而采用力限振動試驗則能夠改善試驗效果,使試驗件動力學響應更加趨近真實[1].

制定試驗條件是開展力限振動試驗最重要的步驟.最理想的情況的是,根據航天器與運載火箭接觸面力實測數據制定試驗條件.但由于實際條件限制,基本沒有接觸面力實測數據可供利用,只能通過理論方法估計力試驗譜(試驗條件).目前常用的力試驗譜估計方法主要有簡單二自由度法、復雜二自由度法和半經驗法[2-4].對于結構復雜的航天器而言,簡單二自由度法和半經驗法忽略了模態因素,并不適用;復雜二自由度法采用的復雜二自由度模型考慮了復雜振動系統的模態行為[5],但該方法并未對如何計算模態有效質量這一關鍵步驟給出具有說服力的論述,理論上仍需完善.

為了能夠更加方便地制定出航天器力限振動試驗的試驗條件,本文提出了一種更加合理的力限振動試驗條件設計方法.該方法對動態子結構理論進行了研究,首次給出了振動系統模態有效質量的詳細推導過程,并依據模態有效質量的分布情況確定不同頻帶內復雜二自由度模型的具體參數,在此基礎上結合激勵條件給出力試驗譜.仿真算例表明,此方法計算結果合理,計算過程較為簡便,適合于工程應用.

1 力限振動試驗概述

1.1 力限振動試驗原理

力限振動試驗[6]是指以加速度作為輸入控制(主動控制),以力作為響應限幅控制(被動控制)的一種振動試驗方法.

在試驗過程中,當傳感器測得的輸入力信號超過了規定的力試驗規范譜值時,控制系統立即調整對振動臺的控制,迫使輸入加速度信號下凹,從而避免過試驗.控制方程如下:

1.2 力限振動試驗的優點

力限振動試驗技術能夠很好地改善試驗件在振動試驗中的動力學環境條件.傳統加速度控制振動試驗容易導致試驗件出現過試驗問題的主要原因在于錯誤地復現了試驗件在實際使用中的安裝阻抗,造成試驗件在共振頻帶上受到過高的輸入力作用.力限振動試驗通過對輸入力的監測,在反共振頻率點上對振動臺的振動量值進行下凹控制,更加真實地模擬了試驗件在實際使用中的動力學邊界條件.

此外,力限振動試驗還能對試驗件質心加速度進行測量.在振動試驗中,為了判斷試驗件承受的載荷是否超過設計極限載荷,需要測量試驗件質心處的振動加速度.但在振動試驗中應用加速度計直接測量質心加速度并不容易,有些試驗件由于質心無法到達或者質心處沒有結構,無法安裝傳感器.即使能夠在質心處安裝上傳感器,試驗件有時還會因共振響應過高而變形,導致質心位置發生變化,導致傳感器無法準確測得試驗件質心的真實響應.若采用力限振動試驗技術,只需根據牛頓第二定律,用測得試驗件與振動臺之間的接觸面力除以試驗件的質量,即可得到試驗件質心加速度.

2 力限振動試驗條件設計

圖 1是振動系統簡化示意圖,源子系統表示火箭或振動臺,負載子系統表示衛星.

圖 1 振動系統簡化示意圖

根據牛頓第二定律,得知接觸面加速度后,再求出負載子系統的動態質量(頻率響應函數),即可算出接觸面力,如下式:

2.1 動態質量的計算

對圖 1所示的負載子系統進行結構離散化,得到負載子系統的動力學平衡方程.

式中,M,K,x和 f分別為系統質量、剛度、位移和外力向量矩陣.將負載子系統的總自由度分為接觸面自由度和內部自由度,則位移向量 x可分為內部位移 xf和接觸面位移 xp兩部分,如式(4)所示.

系統運動方程可寫為分塊矩陣形式:

為了便于算出動態質量,假設負載子系統與源子系統的連接方式為單點連接,則負載子系統的接觸面位移 xp為單自由度位移,試驗件受到基礎結構的激勵形式為單點激勵.

根據模態展開定理,系統位移 x是模態位移q的線性組合[7],即

式中,qf,qp分別為主模態位移和約束模態位移;φff為主模態矩陣稱之為剛體模態矩陣,φfp=-KffKfp,Ipp為單位陣.由于剛體位移不會產生彈性力和阻尼力,所以有

將式(5)和式(6)代入式(4)并前乘 ΦTc得模態坐標半解耦方程:

其中

考慮基礎激勵的情況,有 ff=0,則式(14)可化為

將式(15)代入式(8),并進行傅里葉變換,得

對于每個內部自由度而言,式(16)可化為

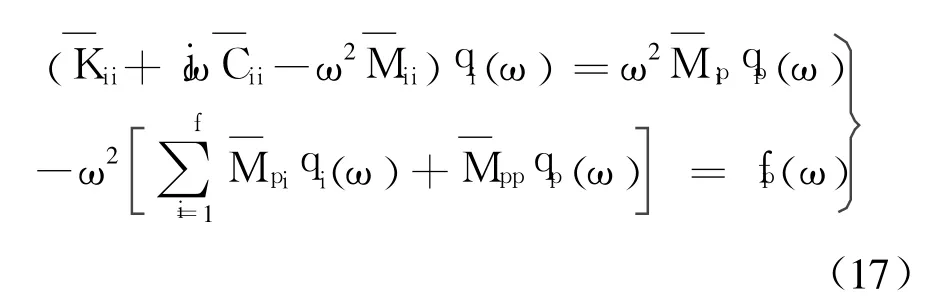
將式(17)第 1個方程代入第 2個方程,整理得

式(18)第 2項為邊界局部效應,其貢獻相對于第 1項可以忽略不計[3].式(18)可化為

其中

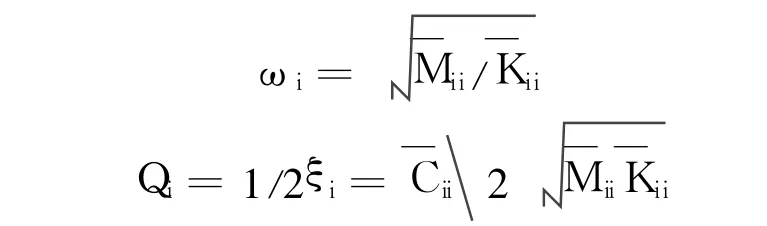
因此,負載子系統的動態質量 Mdyn(ω)為式中,為模態有效質量為模態頻響函數,如下式所示:

模態有效質量則反映了每個模態對系統響應的貢獻大小.假設激振頻率 ω恰好等于第 s階模態的固有頻率 ωs,則激勵力 fp可表示如下:

2.2 力試驗譜的估計

得知源子系統和負載子系統的模態有效質量與模態剩余質量后,在某一頻帶內,振動系統動力學模型可簡化為如圖 2所示的復雜二自由度模型[8].

圖中,m1,c1,k1,M1分別表示源子系統在某一頻帶內的模態有效質量、模態有效阻尼、模態有效剛度和模態剩余質量;m2,c2,k2,M2分別表示負載子系統在某一頻帶內的模態有效質量、模態有效阻尼、模態有效剛度和模態剩余質量;x1,xint和 x2表示源子系統模態有效質量的運動、接觸面運動和負載子系統模態有效質量的運動;F1,Fint和 F2分別表示源子系統模態有效質量上的作用力、接觸面力和負載子系統模態有效質量上的作用力.

復雜二自由度模型的自由振動方程如下:

式中

根據牛頓第二定律和式(24),接觸面力為

在兩個共振頻率處,加速度譜密度較大者為加速度條件,而力譜密度較大者為力限條件[8].計算圖 2所示復雜二自由度系統的傳遞關系,對于源子系統:

對于負載子系統:

負載子系統不受外力作用,則 F2(ω)=0,因而有

如果外力譜在共振頻帶內為恒定值,則應有

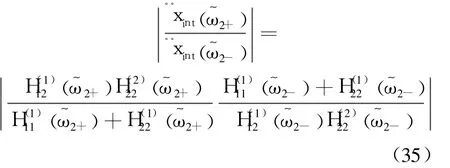
3 仿真算例

本文以某運載火箭為源子系統,某衛星為負載子系統,進行衛星力限振動試驗仿真分析.仿真步驟如下:首先,建立星箭系統的工程桿單元簡單數學模型(僅考慮軸向振動),并根據有限元理論給出源子系統(運載火箭)和負載子系統(衛星)的模型參數;其次,對星箭系統模型施加激勵條件,得到星箭系統接觸面加速度數據,并結合星箭系統模態參數,應用前文介紹的方法制定加速度振動試驗剖面和力限振動試驗剖面;最后,對衛星子系統動力學模型分別加載加速度振動試驗條件、力限振動試驗條件和系統仿真得到的激勵條件,進行振動仿真試驗,將不同激勵條件下衛星子系統動力學模型的振動響應進行比較,分析仿真試驗的效果.

3.1 算例基本信息

本文所用的仿真算例為星箭系統的工程桿單元簡化模型,即一個均勻自由截面、自由-自由邊界的圓柱殼梁.

圖 3中所示等效圓柱殼梁模型的彈性模量E=2×109Pa,質量密度 ρ=4×103kg/m3,截面積A=1×10-3m2,星箭系統全長 LT=1m,其中負載子系統長度為 Ls=0.3 m,源子系統長度 LR=0.7m.

圖 3 星箭系統動力學模型

為了便于分析,本文僅考慮星箭系統的軸向振動,因此,采用僅承受軸向力的一維桿單元進行結構離散化,如圖 4所示.

圖 4 系統單元和節點編號

圖中,負載子系統為 3個單元,源子系統為 7個單元,應用有限元理論計算出星箭系統的系統剛度矩陣(單位 N/m)、質量矩陣(單位 kg)和阻尼矩陣(單位 N·s/m).

關于阻尼陣,在此要說明一點:由于在實際工程結構中,粘滯阻尼系統 C的分布無法確定,因此,本文假設星箭系統是勻質結構,采用瑞利阻尼系統,其中,阻尼系數 α=206.8,β=9.4×10-6.

3.2 衛星子系統加速度仿真振動試驗條件

得到星箭系統工程桿模型的固有參數后,建立系統的狀態方程,即可利用 Matlab仿真模塊建立星箭系統的仿真模型,如圖 5所示.

圖 5中,Simin模塊表示來源于 Matlab工作空間的振動輸入數據文件,文件包含兩列數據,第1列是時間列,第 2列是振動量值;Discrete State-Space模塊為離散狀態方程模塊,是仿真模型的核心部分,狀態方程各個參數由系統剛度矩陣、質量矩陣和阻尼矩陣決定.

圖 5中的黑色細長方框為分路器,能夠將Discrete State-Space模塊計算后的信號按照原來的順序分解成多路信號;Scope～Scope10模塊為仿真模型的輸出模塊,將仿真計算結果輸出至Matlab的工作空間.

圖 5 星箭系統仿真模型

將激振信號文件導入 Matlab工作空間,該信號為某火箭飛行過程中的振動實測數據,如圖 6所示.

圖 6 輸入激振信號

數據導入完畢后,對星箭模型進行仿真分析,仿真結果數據自動存儲在指定路徑,后綴名為“.mat”.“x3.mat”文件為第 4節點的仿真數據,即星箭接觸面加速度.對接觸面加速度譜進行包絡處理,即可得到衛星加速度控制仿真振動試驗條件,如圖 7所示.

3.3 衛星子系統力限振動試驗條件

根據本文第 2節介紹基于復雜二自由度模型的力限振動試驗條件設計方法,編寫 Matlab算法,以仿真算例的固有參數作為輸入條件,計算衛星子系統的力限振動試驗條件,如圖 8所示.

3.4 衛星子系統仿真振動試驗分析

把振動臺簡化為一個小質量的質量-彈簧-阻尼系統,然后把衛星安裝到臺面上,分別施加加速度包絡試驗條件和力限試驗條件,計算系統的頻響特性,比較試驗效果.星臺振動系統如圖 9所示.

圖 7 衛星加速度控制仿真振動試驗條件

圖 8 衛星子系統的力限振動試驗條件

圖 9 星臺振動系統示意圖

建立星臺振動系統的 Matlab仿真模型(見圖10).圖中,Subsystem模塊為振動臺子系統,Subsystem1,Subsystem2,Subsystem3,Subsystem4分別代表衛星子系統的 4個節點;simin模塊為輸入模塊,用于輸入振動試驗條件;衛星各個節點的振動響應分別存儲在 x1.mat,x2.mat,x3.mat,x4.mat模塊中.

分別將復雜二自由度法得到的力試驗譜以及傳統加速度試驗條件輸入到仿真模型的 simin模塊中,以和第 4節點為響應觀測點,觀察星箭系統仿真試驗的試驗效果,如圖 11所示.

從衛星結構的響應曲線來看,使用由復雜二自由度法獲取的力試驗譜進行輸入力響應限幅控制,在衛星結構的共振頻帶上能夠很好地緩解傳統加速度振動試驗條件導致的過試驗現象.

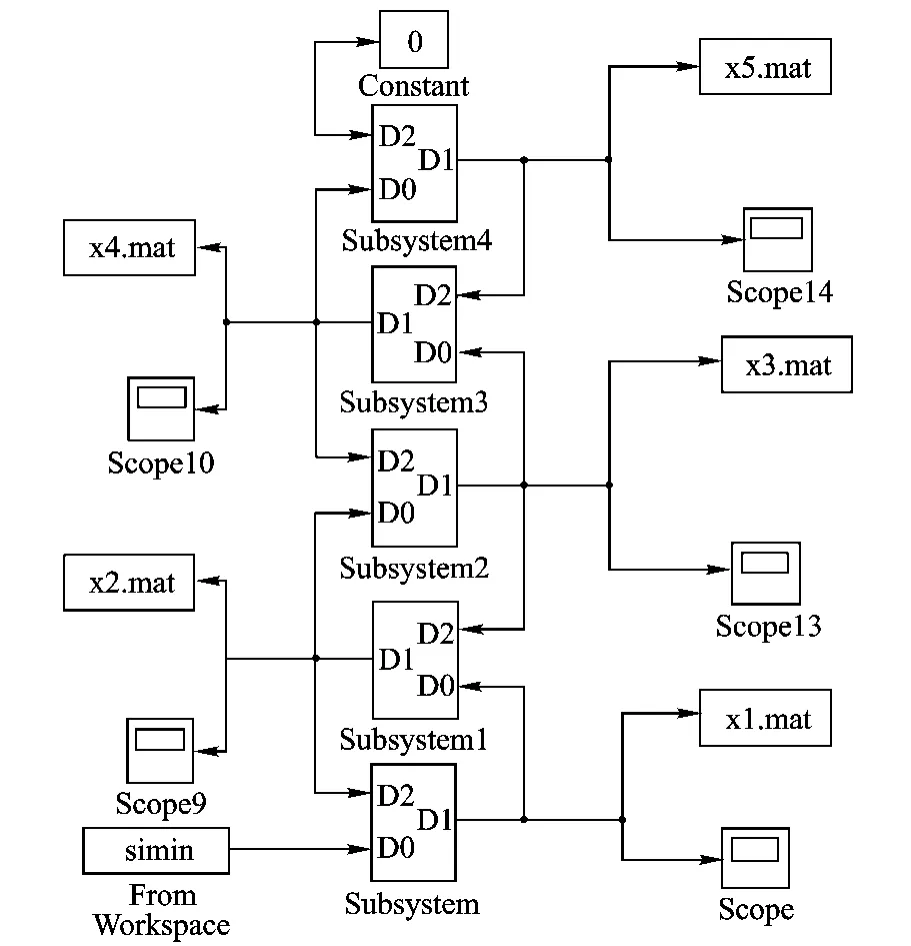
圖 10 Matlab星臺振動仿真模型

圖 11 星臺系統仿真振動試驗 4號節點響應譜

4 結 論

本文對受基礎激勵作用試驗件的力限振動試驗條件的確定方法進行了研究.根據結構動力學理論,結合工程經驗,給出了受基礎激勵作用試驗件的力限振動試驗條件設計方法.

經過本文的分析研究,形成以下幾點認識:

1)動態質量的精度依賴于試驗件離散化后的自由度,自由度越大精度越高,但計算量也會越來越大,因此應對動態質量的精度和計算效率進行權衡.

2)由于本文方法的理論假設是單點激勵,因此給出的力試驗譜略顯保守,若能擴展到多點激勵,結果會更加合理,但需要進行進一步地研究.

3)由測點振動響應譜可知,本文方法給出的力限振動試驗條件能將試驗件過試驗因子降低為傳統加速度試驗條件作用下的 0.01.

References)

[1]Dharanipathi Vijayamohan Rao.Investigation of the semi-empirical method for force lim ited vibration testing[D].Quebec:Department of Mechanical and Industrial Engineering,Concordia U-niversity,2003

[2]NASA-HDBK-7005 Dynamic environmental criter[S]

[3]Andre Cote,Ramin Sedaghati.Force limited vibration complex two degree of freedom system method[J].AIAA Journal,2004,42(6):1208-1218

[4]NASA-HDBK-7004B Force limited vibration testing[S]

[5]Soucy Y,Dharanipathi V.Investigation of force limited vibration for reduction of overtesting[J].Journal of Spacecraft and Rockets,2006,43(4):866-876

[6]Scharton T.Force limited vibration testing monograph[R].NASA Reference Publ RP-1403,1997

[7]邱吉寶,向樹紅,張正平.計算機構動力學[M].合肥:中國科學與技術大學出版社,2009 Qiu Jibao,Xiang Shuhong,Zhang Zhengping.Computational structures dynamics[M].Hefei:University of Science and Technology of China Press,2009(in chinese)

[8]Davis Gregory L.An analysis of nonlinear stiffness and damping effects in force-limited random vibration testing[D].Houston:Rice University,1998

(編 輯 :婁 嘉)

Design method for specification of force-limited vibration testing

Mo Changyu Yuan Hongjie

(School of Reliability and Systems Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

The method based on the comp lex two degrees of freedom system(TDFS)mode to design the specification of force-limited vibration testing was proposed.In the method,dynamic sub-structure was adopted to calculate modal effective mass and modal residual mass of specimen structure and supporting structure.The complex TDFSmodel parameter of vibration system in different frequency bands was defined according to the distribution of mode effective mass in frequency domain.The force spectrum and acceleration spectrum of contact surface between specimen and supporting structure was defined with the excitation condition of supporting structure.Spectrum envelope is the force-limited vibration test profile.Simulation results demonstrate that the force-limited vibration test conditions defined by this method is much more reality on vibration environment than conventional acceleration test condition.

complex TDFS;force-limited;modal effectivemass

O 32;V 1

A

1001-5965(2011)04-0439-07

2010-01-25

莫昌瑜(1985-),男,海南文昌人,碩士生,moyu_0513@163.com.