電力系統風電場節點模型研究及潮流計算

王林川，韓寶國，李會杰，姜 寧

(東北電力大學電氣工程學院，吉林吉林132012)

0 引言

風能是一種可再生的綠色能源，近年來能源結構的調整使分布式發電特別是風力發電所占的比例越來越高。由于風力所具有的間歇性和隨機性的特點，使大規模風電在并網運行時給電網帶來了一些不利影響，例如電壓閃變、諧波污染等。因此，有必要對風電場節點模型進行深入研究。含風電場的電力系統潮流計算［1］的關鍵在于異步機模型的建立。在電力系統潮流計算中，傳統節點主要分為PQ節點、PV節點及平衡節點。文獻［2-3］將風電場節點作為PQ節點，即根據給定風速和功率因數求得有功和無功功率，但是PQ節點不能從本質上反映風電的特點而限制了其應用。文獻［4］在計算潮流時考慮了節點電壓對異步機吸收無功功率的影響，模型較為精確，但是沒有考慮異步機的滑差的變化對有功輸出的影響。文獻［5］提出了RX模型，模型考慮了風力機的輸出特性，比其它模型完善，但在模型中有2個迭代過程:常規潮流迭代計算和異步機的滑差迭代計算，因此迭代次數增加，影響收斂速度。為此，提出在傳統RX模型的基礎上對其進行改進，以使之更為完善。改進的模型充分考慮了異步機的原動力和滑差之間的函數關系、無功-電壓特性。在修正方程中，引入了異步機的滑差修正量，將異步機的無功作動態變化，相應的對雅克比矩陣加以修正，與傳統RX模型相比，不僅保證了迭代過程具備牛頓-拉夫遜法的平方收斂性，而且保持計算的準確性。

1 風力機模型

風電機組主要由風力機和異步機等主要元件組成。風能的功率與風速的三次方成正比［6］，其表達式為

式中ρ為空氣密度，kg/m3;V為風速，m/s;A為風力機的掃掠面積，m2;Cp為風力機的風能利用系數，是表征風力機效率的重要參數，表明風輪機從風中獲得的有用風能的比例，根據貝茨理論最大可達到16/27。風能利用系數Cp與尖速比Ttsr(tip speedratio)有關，兩者之間函數關系由試驗得出，還可以根據已有的試驗數據用插值法［7］來計算風力機的風能利用系數Cp值。其中，尖速比Ttsr是葉輪尖的線速度與風速的比值，其表達式為

式中Ttsr為尖速比;R為葉片半徑，m;ω為風輪在風速為v時的旋轉角頻率，rad/s。

2 異步發電機數學模型

大型風電場多數采用異步機，因而以異步機為主要研究對象。風電場中風力機在超同步速下運行，此時，異步機吸收風力機提供的機械能，發出有功功率，同時吸收無功功率，提供其建立磁場所需要的勵磁電流。異步機簡化等值電路如圖1所示。

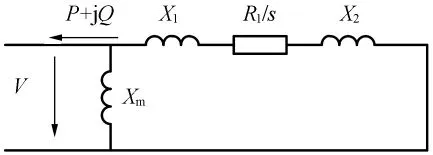
圖1 異步機簡化等值電路圖

在圖1中，R2為轉子電阻，X2為轉子電抗，X1為定子漏抗，Xm為勵磁電抗，s為滑差，忽略定子電阻R1。

由異步機等值電路圖可得到以下函數關系為

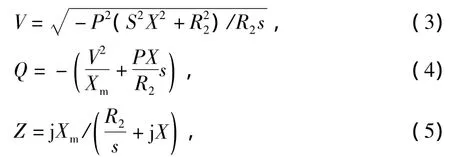
式中Z為異步機的等值阻抗，X=X1+X2。

異步機發出的有功功率為

式中R2為風力異步發電機的轉子電阻，Ω;s為異步機滑差，其計算式為s=(ns-nrkr)/ns×100%;nr為葉片的旋轉速度;k為齒輪比;ns為同步轉速，ns=60f/p;f為電網頻率;p為異步機極對數。

從表達式(6)可以看出，當滑差發生變化時，異步機發出的有功隨之變化。由能量守恒定律，異步機吸收的機械功率和發出的有功功率應該相等。在迭代過程中，當這兩個功率不相等時，應該對滑差進行修正，為此在潮流計算時引入了滑差修正量。另一方面，根據異步機等值電路圖可以得到無功-電壓特性方程，由于異步機吸收的無功功率是機端電壓的函數，因此根據式(5)得到如下關系式為

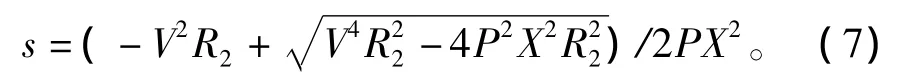
將式(7)帶入式(6)可得異步機的無功-電壓特性方程為

在潮流計算中綜合考慮異步機有功功率特性和無功—電壓特性函數可以得到以下修正方程為

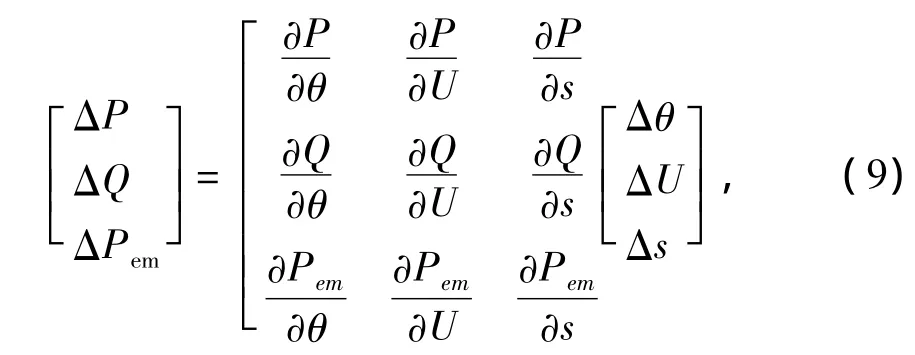
對應風電機組節點的功率為

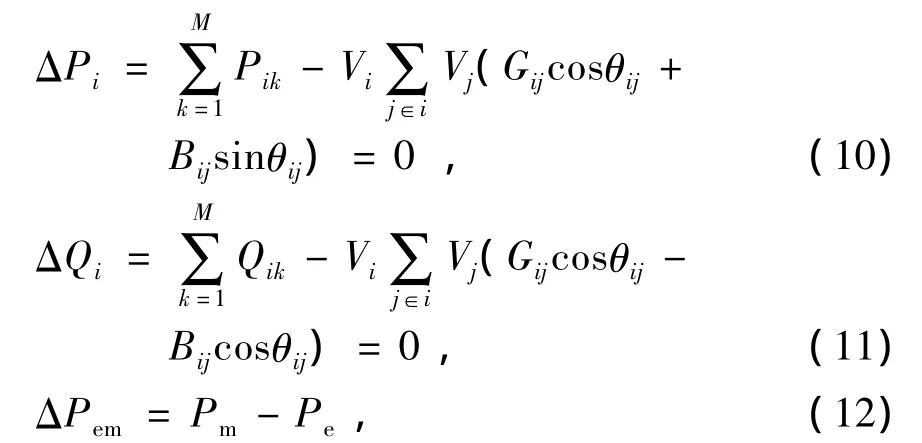
式中M為并聯運行的等值風電機組臺數;Pik和Qik為第k臺等值機組的有功和無功出力。其中Pik由風電場風速決定，Qik是機端電壓的函數，由式(8)確定。{ΔPem}為列向量，表示風電場中風力機的機械功率和電磁功率的差值，其維數為等值風力機組臺數。在模擬風電場時忽略了尾流效應［8］對異步機有功出力的影響，為了減小雅克比矩陣維數、縮短計算時間，將型號和風力狀況相同的異步機等值為1臺等值機。

當引入ΔPem后，其迭代過程的收斂判據為

式中，ε為1個給定的小正數。Δs是異步機的滑差修正量，其計算式為

運用牛頓-拉夫遜方法進行潮流計算時，只需要修改雅克比矩陣中的對應元素就可，其它元素的表達式無需變化。

3 算例分析

風電場通過變壓器和110 kV線路接入IEEE14節點標準測試系統的14號節點，如圖2所示，應用MATLAB實現算法。

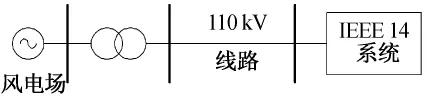
圖2 風電場接入IEEE14系統圖

風力系統參數參考文獻［9］。風電場接入系統線路參數為12.6+j 24.96 Ω。風電場容量為20× 600 kW，電場中風電機組分為2排，排間距為120 m，輪轂處的高度為50 m，假定風電場空氣密度為1.224 5 kg/m3，風力機的掃略面積為1 840 m2，風能利用系數Cp與尖速比Ttsr的函數關系如表1所示。忽略尾流效應，即風電機組的切入、切出、額定風速均相同，分別為3 m/s、20 m/s、13.5 m/s，額定電壓為690 V，異步機定子阻抗為0.004 53+j 0.050 7 Ω，轉子阻抗為0.004 86+j 0.149 1 Ω，勵磁電抗為2.205 9 Ω。

風電場分別采用RX模型、改進RX模型進行潮流計算，將不同風速下異步機的輸出功率和機端電壓進行比較，同時還比較迭代次數，數據如表2—表4所示。

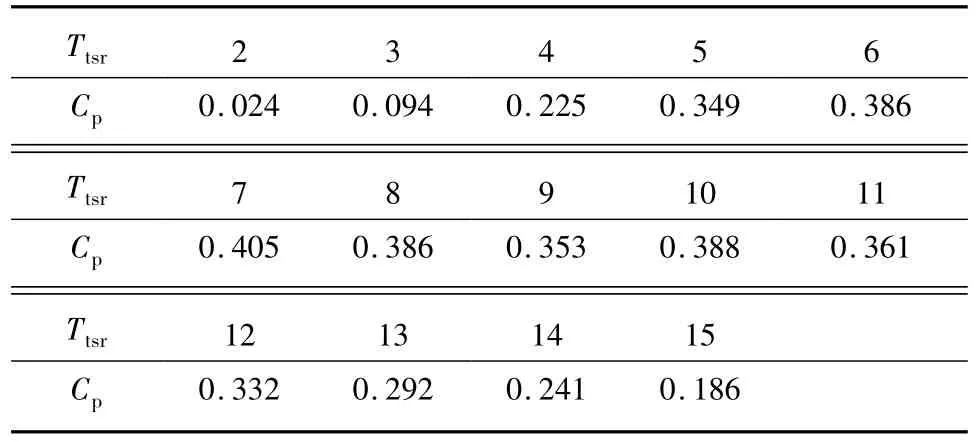
表1 風能利用系數與尖速比的關系

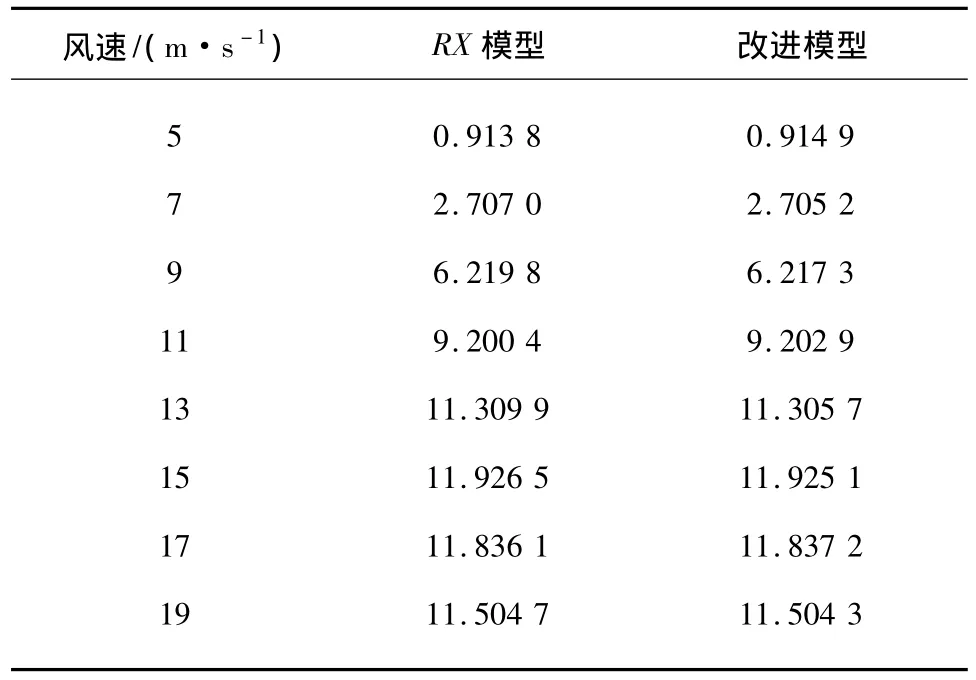
表2 異步機有功輸出結果

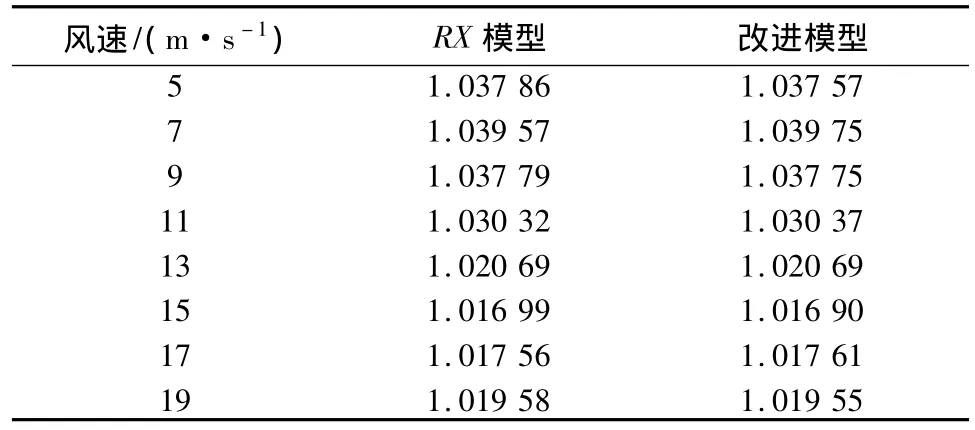
表3 風電場出口電壓對比

表4 迭代次數對比

對比以上表格中的數據可以看出，改進模型和RX模型計算結果基本一致，保證了計算的精確性，但是達到相當精確性所用的迭代次數明顯減少，縮短了計算時間。

4 結論

通過應用Matlab實現算法對比分析改進RX模型與RX模型，得出以下結論。

a.考慮了異步機的輸出功率特性和無功-電壓特性，使改進RX模型更加完善。

b.在保持潮流計算精確性的基礎上提高了收斂速度。

［1］ 雷亞洲.與風電并網相關的研究課題［J］.電力系統自動化，2003，27(8):84-89.

［2］ Chen Z，Spooner E.Grid power quality with variable speed wind turbines［J］.IEEE Trans on Energy Conversion，2001，16(2):148-154.

［3］ Saad-Saoud Z，Jenkins N.Models for predicting flicker induced by large wind turbines［J］.IEEE Transactions on Energy Conversion，1999，14(3):743-748.

［4］ 陳金富，陳海焱，段獻忠.含大型風電場的電力系統多時段動態優化潮流［J］.中國電機工程學報，2006，26(3):31-35.

［5］ Feijoo AE，Cidras J.Modeling of wind farms in the load flow analysis［J］.IEEE Trans on Power Systems，2000，15(1):110-115.

［6］ 陳樹勇，戴慧珠，白曉民，等.風電場的發電可靠性模型及其應用［J］.中國電機工程學報，2000，20(3):26-29.

［7］ 何光渝.Visual C++常用數值算法集［M］.北京:科學出版社，2002.

［8］ 申洪，王偉勝.一種評價風電場運行情況的新方法［J］.中國電機工程學報，2003，23(9):90-93.

［9］ 張伯明.高等電力系統分析［M］.北京:清華大學出版社，1996.