AZ31鎂合金早期力學(xué)性能退化非線性超聲檢測(cè)

吳 斌, 顏丙生, 何存富, 焦敬品

(北京工業(yè)大學(xué)機(jī)械工程與應(yīng)用電子技術(shù)學(xué)院,北京 100124)

金屬零部件由于承受載荷而產(chǎn)生力學(xué)性能退化,其壽命一般可分為三個(gè)階段：早期的力學(xué)性能退化(位錯(cuò)群的大量產(chǎn)生以及駐留滑移帶(Persistent slip bands,PSBs)和微裂紋的形成)、損傷的起始與積累(微裂紋的成核長大和宏觀裂紋的產(chǎn)生)以及最后的斷裂失效[1]。對(duì)于設(shè)計(jì)良好的結(jié)構(gòu)元件,第一和第二階段一般占整個(gè)壽命的 80%～90%[2],因此發(fā)展金屬材料早期力學(xué)性能退化的有效檢測(cè)和評(píng)價(jià)手段就顯的十分重要。

超聲無損檢測(cè)技術(shù)利用波的時(shí)程、聲速和衰減等物理參數(shù)已經(jīng)可以對(duì)構(gòu)件壽命的第三階段進(jìn)行有效的檢測(cè)和評(píng)估[3]。但是,上述線性物理參數(shù)對(duì)材料和結(jié)構(gòu)早期力學(xué)性能退化并不敏感[4]。近期相關(guān)實(shí)驗(yàn)研究表明金屬材料的早期力學(xué)性能退化與超聲波的非線性效應(yīng)密切相關(guān)[5-10]。在金屬材料的早期力學(xué)性能退化階段,由于位錯(cuò)和滑移帶等微觀缺陷的存在,當(dāng)單一頻率的超聲波在金屬材料內(nèi)部傳播時(shí)會(huì)使波形發(fā)生畸變,從而產(chǎn)生高次諧波。因此,通過對(duì)這些高次諧波的檢測(cè),可以對(duì)材料和結(jié)構(gòu)的早期力學(xué)性能退化做出有效的無損檢測(cè)和評(píng)估。

非線性超聲無損檢測(cè)技術(shù)一直是研究的熱點(diǎn)。Nagy PB[4]通過實(shí)驗(yàn)比較了超聲線性和非線性參數(shù)對(duì)材料疲勞失效的敏感程度。指出隨著疲勞次數(shù)的增加,非線性系數(shù)明顯增加,但是線性參數(shù)(衰減、聲速等)卻沒有發(fā)生明顯變化。Yost and Cantrell[7]從實(shí)驗(yàn)上驗(yàn)證了疲勞引起的位錯(cuò)對(duì)超聲非線性系數(shù)的影響。Kyung-Young Jhang[6]采用一維縱波模型,使用PZT探頭離線檢測(cè)了鋁合金材料的非線性系數(shù),得出了二次諧波和非線性系數(shù)都隨疲勞次數(shù)增加的結(jié)論,但實(shí)驗(yàn)結(jié)果有較大的分散性。Jin-Yeon Kim等[9]用PZT探頭對(duì)鎳基合金疲勞損傷的超聲非線性行為進(jìn)行了實(shí)驗(yàn)研究,主要是對(duì)實(shí)驗(yàn)系統(tǒng)進(jìn)行了優(yōu)化,分別離線測(cè)量了低周和高周疲勞試件的非線性系數(shù),指出高周疲勞的實(shí)驗(yàn)結(jié)果分散性更大。徐從元等[11]用壓電換能器測(cè)定了四個(gè)不同疲勞損傷程度下LY-12鋁合金棒的非線性系數(shù)、聲速和衰減。根據(jù)測(cè)量結(jié)果指出疲勞引起的聲速和衰減的變化遠(yuǎn)小于非線性系數(shù)的變化。稅國雙等[12]對(duì)非線性超聲無損檢測(cè)技術(shù)的研究現(xiàn)狀進(jìn)行了綜述,指出了非線性超聲在金屬疲勞檢測(cè)中的應(yīng)用前景。

盡管非線性超聲無損檢測(cè)技術(shù)具有廣闊的應(yīng)用前景,但仍然沒有成功地應(yīng)用于工程實(shí)際。針對(duì)鎂合金構(gòu)件在復(fù)雜工作條件下抗疲勞性能差的問題[13,14],發(fā)展了一套可靠的超聲非線性系數(shù)測(cè)試實(shí)驗(yàn)系統(tǒng),利用該系統(tǒng)進(jìn)行了鎂合金拉伸和疲勞非線性超聲檢測(cè)實(shí)驗(yàn),并對(duì)拉伸試件進(jìn)行了原位微觀觀察。

1 超聲非線性理論

由于固體介質(zhì)的材料非線性,單一頻率正弦超聲波將與固體介質(zhì)間產(chǎn)生非線性相互作用,從而產(chǎn)生高次諧波,為了有效反應(yīng)這一特點(diǎn),Cantrell,Breazeal等人[15]建立了固體介質(zhì)內(nèi)的非線性超聲波動(dòng)方程：

其中ρ0為介質(zhì)密度,K2為二階彈性常數(shù)(second-order elastic constants,SOE),且K2與縱波波速的關(guān)系有K2=ρ0c2,K3為三階彈性常數(shù)(third-order elastic constants,TOE)。若定義非線性系數(shù)為[16,17]：

并設(shè)方程(1)的初始條件為：

用逐級(jí)近似微擾法可求得方程(1)的解為[15]：

其中k=ω/c為波數(shù)。由(4)式可知,基波幅值為：

二次諧波幅值為：

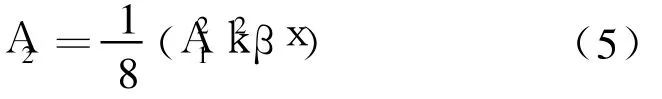
進(jìn)而可以得到材料的非線性系數(shù)為：

根據(jù)方程(6),對(duì)于給定的聲波頻率和波傳播距離,通過對(duì)基波和二次諧波幅值A(chǔ)1和 A2的測(cè)量,就可以確定材料的超聲非線性系數(shù)。

固體材料的非線性主要來自兩個(gè)方面：(1)構(gòu)成材料的原子間相互作用力(或點(diǎn)陣)的非簡諧性; (2)材料內(nèi)部的位錯(cuò)、滑移帶和微裂紋等微觀缺陷。研究表明,由位錯(cuò)等微觀缺陷引起的非線性比由原子點(diǎn)陣的非簡諧性引起的非線性大得多[2]。金屬作為一種晶體,其力學(xué)性能退化與其中位錯(cuò)的運(yùn)動(dòng)存在密切的關(guān)系,周期性疲勞載荷的作用下,金屬材料內(nèi)部的位錯(cuò)弦長、位錯(cuò)密度、位錯(cuò)組態(tài)和滑移帶等微觀結(jié)構(gòu)將發(fā)生變化,從而使超聲非線性系數(shù)有較顯著的改變[18]。因此超聲非線性系數(shù) β可以用作描述介質(zhì)非線性的量化指標(biāo),特別是對(duì)材料的早期疲勞壽命預(yù)測(cè)將具有重要的實(shí)際意義。

在本實(shí)驗(yàn)中,為了研究方便,采用 β=A2/A21來表征超聲非線性系數(shù)的變化情況。顯然,它與材料的絕對(duì)非線性系數(shù)成正比。

2 實(shí)驗(yàn)系統(tǒng)與測(cè)量方法

圖1所示為超聲非線性系數(shù)測(cè)量系統(tǒng)。系統(tǒng)主要包括信號(hào)發(fā)生器 33220A、功率放大器 AG1016, MTS810材料疲勞實(shí)驗(yàn)機(jī)、高能低通濾波器、衰減器、傳感器、示波器、計(jì)算機(jī)以被檢測(cè)試件和夾具。

圖1 實(shí)驗(yàn)系統(tǒng)示意圖Fig.1 The layoutof experimental system

整個(gè)實(shí)驗(yàn)系統(tǒng)采用透射法測(cè)量基波和二次諧波的幅值。信號(hào)發(fā)生器產(chǎn)生的單頻正弦波經(jīng)放大、濾波后,驅(qū)動(dòng)固定于被測(cè)試件一端的壓電傳感器,向試件中輸入單頻超聲波。位于試件另一端的壓電傳感器將采集傳來的包含有高頻成分的超聲波信號(hào),然后對(duì)采集到的信號(hào)進(jìn)行FFT變換,最終得到基波和二次諧波的幅值,進(jìn)而確定非線性系數(shù)的值。

采用美國RETIC公司的高能低通濾波器來濾除功率放大器射頻門產(chǎn)生的高頻干擾。衰減器把從濾波器引出的一路信號(hào)衰減后作為監(jiān)測(cè)信號(hào)輸入示波器,通過監(jiān)測(cè)信號(hào)可以控制輸入發(fā)射傳感器信號(hào)的幅值。一對(duì)中心頻率分別為5MHz和10MHz的Panametrics窄帶PZT超聲探頭作為發(fā)射和接收傳感器。由于進(jìn)行非線性測(cè)量時(shí),激勵(lì)信號(hào)幅值較大,普通耦合劑容易揮發(fā),采用比較穩(wěn)定的鋰基黃油作為耦合劑。一個(gè)特殊的夾具來保證檢測(cè)時(shí)探頭和試件之間的充分和穩(wěn)定的耦合,同時(shí)保持發(fā)射傳感器和接收傳感器在同一軸線上,以免能量損失。

圖2為試件尺寸示意圖,板厚7.5mm,材料為AZ31鎂合金。半徑為 157mm的圓弧中心處作為疲勞實(shí)驗(yàn)時(shí)的預(yù)設(shè)應(yīng)力集中區(qū)域。試件表面均經(jīng)過仔細(xì)的打磨拋光。共兩組試件,第一組共一個(gè)試件用于拉伸實(shí)驗(yàn),第二組共三個(gè)試件用于疲勞實(shí)驗(yàn)。

圖2 試件尺寸示意圖(尺寸/mm)Fig.2 Dimensions of specimen(mm)

為了減少儀器和隨機(jī)因素產(chǎn)生的諧波干擾,取試件在厚度方向所能容納的不與接收信號(hào)重疊的最大周期數(shù)作為正弦脈沖串信號(hào)周期數(shù)。根據(jù)超聲波傳播的距離和波速,確定本實(shí)驗(yàn)激勵(lì)信號(hào)周期數(shù)為7。圖 3a為接收時(shí)域信號(hào),對(duì)接收到的時(shí)域信號(hào)進(jìn)行FFT變換,在頻率為5MHz的基頻位置上可以得到基波幅值A(chǔ)1,如圖3b實(shí)線所示;在10MHz的二倍頻位置上可以得到二次諧波幅值 A2,如圖3b虛線所示。

3 實(shí)驗(yàn)結(jié)果與分析

3.1 二次諧波幅值與基波幅值平方的關(guān)系

首先利用上述實(shí)驗(yàn)方法和裝置對(duì)同一試件測(cè)量其在不同輸入電壓時(shí)的基波和二次諧波幅值,信號(hào)源電壓取值范圍為220mV到 320mV之間,間隔10mV。對(duì)測(cè)量到的實(shí)驗(yàn)數(shù)據(jù)進(jìn)行線性擬合,得到圖4所示測(cè)量 1的二次諧波幅值和基頻波幅值平方的關(guān)系曲線,最佳擬合曲線方程為：

圖3 基波和二次諧波幅值 (a)接收時(shí)域信;(b)基波和二次諧波幅值Fig.3 Amplitude of the fundamental wave and the second-harmonic wave (a)Received time domain signals; (b)Fundamentaland 2nd harmonic amplitude

圖4 二次諧波幅值與基波幅值平方的關(guān)系Fig.4 Second-harmonic amplitude versus the amp litude of the fundamental squared

線性相關(guān)系數(shù)r=0.9986。

然后將傳感器從試件拆除,完全清理耦合劑后重新安裝,進(jìn)行第二次測(cè)量。得到圖 4所示測(cè)量 2的二次諧波幅值和基頻波幅值平方的關(guān)系曲線,最佳擬合曲線方程為：

線性相關(guān)系數(shù)r=0.9984。

3.2 準(zhǔn)靜態(tài)拉伸實(shí)驗(yàn)結(jié)果

利用夾具把試件安裝在MTS810全自動(dòng)材料疲勞實(shí)驗(yàn)機(jī)上進(jìn)行準(zhǔn)靜態(tài)拉伸實(shí)驗(yàn)。首先測(cè)量未拉伸試件的非線性系數(shù) β0,然后拉伸到不同的應(yīng)力時(shí)停止加載,測(cè)量試件的非線性系數(shù) β,用 β/β0對(duì)超聲非線性系數(shù)進(jìn)行歸一化,同時(shí)測(cè)量其應(yīng)變。

圖5 歸一化后的非線性系數(shù)與拉伸應(yīng)力的關(guān)系Fig.5 Normalized nonlinearity parameter versus stress level

表1 拉伸試件的應(yīng)力和應(yīng)變Table 1 Stress and Strain ofmonotonic tensions specimen

圖5為歸一化后的超聲非線性系數(shù)與拉伸應(yīng)力之間的關(guān)系。可以分為兩個(gè)階段,在屈服前的彈性階段,超聲非線性系數(shù)沒有明顯的增長變化;在塑性階段,隨著拉伸應(yīng)力的增大,超聲非線性系數(shù)近似單調(diào)增加。表 1為試件的應(yīng)力與應(yīng)變對(duì)應(yīng)關(guān)系。

3.3 拉伸試件原位微觀觀察

為了在微觀結(jié)構(gòu)上對(duì)實(shí)驗(yàn)結(jié)果進(jìn)行驗(yàn)證,采用原位微觀觀察法對(duì)試樣表面的位錯(cuò)滑移進(jìn)行觀察。觀測(cè)儀器為KEYENCE VH-2500數(shù)字顯微鏡。試樣如圖 6所示。首先對(duì)試樣的應(yīng)力集中區(qū)表面進(jìn)行打磨、拋光、腐蝕,在光學(xué)顯微鏡下觀察試樣的原始形貌。然后將試樣在MTS810全自動(dòng)材料疲勞實(shí)驗(yàn)機(jī)上施加單調(diào)拉伸應(yīng)力。在不同應(yīng)力階段,對(duì)試樣的同一位置進(jìn)行微觀觀察。

圖6 微觀觀察試樣Fig.6 The specimen ofopticalmicrostructures

實(shí)驗(yàn)所用腐蝕液為硝酸(1%)、草酸(0.5%)、乙酸(0.5%)和水(98%)混合溶液,腐蝕時(shí)間15s。在對(duì)試樣拉伸加載的過程中,利用脫脂棉覆蓋試樣以保證觀察面的清潔。

圖7給出了拉伸試樣在不同應(yīng)力階段下的光學(xué)顯微圖。從圖中可以看出在原始和彈性階段微觀結(jié)構(gòu)基本沒有變化。進(jìn)入塑性階段后,應(yīng)力為 200MPa時(shí),沿晶界的位錯(cuò)滑移增多;應(yīng)力為227MPa時(shí)位錯(cuò)滑移大量出現(xiàn),晶界發(fā)生明顯變形。

圖7 不同應(yīng)力階段下拉伸試件的光學(xué)顯微圖Fig.7 Opticalm icrostructures ofmonotonic tensions specimen under different loading stress (a)Original;(b)80MPa;(c)200MPa;(d)227MPa

金屬材料的塑性變形主要是通過位錯(cuò)運(yùn)動(dòng)實(shí)現(xiàn)的。根據(jù)文獻(xiàn)[7],金屬材料的非線性源于晶格的非諧和以及在施加一定外載荷情況下晶體內(nèi)部出現(xiàn)的位錯(cuò)和滑移帶等微觀缺陷。在彈性階段,金屬材料內(nèi)部微結(jié)構(gòu)還沒有發(fā)生明顯變化,所以只存在由晶格的非諧和造成的金屬材料固有非線性產(chǎn)生的諧波。進(jìn)入塑性變形階段后晶體內(nèi)部位錯(cuò)密度和位錯(cuò)滑移等微觀缺陷產(chǎn)生,非線性系數(shù)也會(huì)隨之增大。因此,該實(shí)驗(yàn)結(jié)果是合理的。

宏觀力學(xué)(應(yīng)力、應(yīng)變)、非線性超聲檢測(cè)和微觀觀察實(shí)驗(yàn)結(jié)果表明材料的超聲非線性系數(shù)、應(yīng)力應(yīng)變和內(nèi)部微觀結(jié)構(gòu)存在一定的關(guān)系。非線性系數(shù)β作為宏觀和微觀的橋梁可以表征材料的力學(xué)性能退化情況。

3.4 疲勞實(shí)驗(yàn)結(jié)果

疲勞試件共有A,B和C三個(gè)。A和B分別在MTS810全自動(dòng)材料疲勞實(shí)驗(yàn)機(jī)上進(jìn)行拉壓疲勞,疲勞加載頻率10Hz,R=σmin/σmax=-1。為了觀察不同疲勞周數(shù)對(duì)實(shí)驗(yàn)結(jié)果的影響,給A試件較大的加載應(yīng)力,取屈服極限的±65%(±129MPa),A試件的疲勞壽命為66500周;給B試件加載應(yīng)力取屈服極限的±60%(±119MPa),B試件的疲勞壽命為113200周。C試件在疲勞實(shí)驗(yàn)機(jī)上進(jìn)行拉 -拉疲勞,疲勞加載頻率10Hz,R=σmin/σmax=0.1,加載應(yīng)力為18.9 MPa-189MPa,C試件的疲勞壽命為43600周。因?yàn)椴牧掀诒旧淼姆稚⑿院驮嚰膫€(gè)體差異,相同的試件在相同的實(shí)驗(yàn)條件下疲勞壽命并不一定相同。

首先測(cè)量未疲勞試件的非線性系數(shù) β0,然后每隔固定周數(shù)停止疲勞加載,測(cè)量試件的非線性系數(shù)β,用 β/β0對(duì)超聲非線性系數(shù)進(jìn)行歸一化。用疲勞壽命的百分?jǐn)?shù)即試件不同循環(huán)加載周次與疲勞壽命的比值來表示疲勞損傷的程度。

圖8給出了A,B和C試件歸一化后的非線性系數(shù)與疲勞壽命的關(guān)系曲線。從圖中可以看出,隨著疲勞周數(shù)的增加,歸一化后的相對(duì)非線性系數(shù)整體呈增長趨勢(shì),特別是疲勞早期近似于單調(diào)增加。雖然每個(gè)試件的實(shí)驗(yàn)結(jié)果存在一定差異,但曲線整體變化趨勢(shì)相似,說明該組曲線可以表征材料疲勞早期退化的某種規(guī)律。每條曲線都可以分為兩個(gè)階段,第一階段在疲勞壽命的 55%左右之前,超聲非線性系數(shù)隨疲勞周數(shù)的增加明顯單調(diào)增加。第二階段在疲勞壽命的 55%左右之后,非線性系數(shù)開始減小并出現(xiàn)較大波動(dòng)。

圖8 A,B和C試件非線性系數(shù)與疲勞壽命的關(guān)系Fig.8 Normalized non linearity parameter versus fatigue life

在疲勞壽命的早期階段,隨著疲勞周數(shù)的增加,位錯(cuò)弦長、位錯(cuò)偶間距和位錯(cuò)密度增大,晶帶滑移出現(xiàn)和增多,非線性系數(shù)也逐漸增大,當(dāng)微裂紋開始萌生時(shí)非線性系數(shù)達(dá)到峰值。從實(shí)驗(yàn)結(jié)果看,與文獻(xiàn)[9]的實(shí)驗(yàn)結(jié)果在數(shù)值和趨勢(shì)上基本一致,說明非線性超聲方法同樣適用于AZ31鎂合金。然后在疲勞壽命的晚期,位錯(cuò)密度趨于飽和,大量微裂紋開始出現(xiàn),裂紋的存在使材料的衰減系數(shù)增大。而且超聲衰減系數(shù)與頻率的平方成正比,使二次諧波幅度衰減大于基波幅度衰減,非線性系數(shù)有所下降。另外,在疲勞壽命的后期,試件變形造成探頭和試件之間耦合質(zhì)量的下降,裂紋的開閉等因素也會(huì)使非線性系數(shù)的值減小和出現(xiàn)較大波動(dòng)。

實(shí)驗(yàn)結(jié)果表明,金屬材料超聲非線性系數(shù)與疲勞壽命之間的關(guān)系可以用來表征材料的疲勞過程,如果事先對(duì)某種零部件的超聲非線性系數(shù)曲線進(jìn)行標(biāo)定,則有望利用非線性超聲無損檢測(cè)技術(shù)來預(yù)測(cè)在役零部件的疲勞壽命。

A,B和 C試件的實(shí)驗(yàn)結(jié)果沒有明顯的規(guī)律性區(qū)別,說明在低周疲勞范圍內(nèi),加載應(yīng)力的大小以及拉-拉和拉-壓疲勞模式的變化對(duì)實(shí)驗(yàn)結(jié)果沒有明顯的影響。

另外注意到,金屬材料疲勞實(shí)驗(yàn)結(jié)果相比于拉伸實(shí)驗(yàn)結(jié)果雖然整體增長趨勢(shì)相同,但具有更大的分散性,特別是在疲勞后期。這主要有兩個(gè)原因, (1)實(shí)際實(shí)驗(yàn)時(shí)金屬材料疲勞本身具有一定的分散性;(2)在疲勞壽命的后期材料內(nèi)部會(huì)有大量疲勞裂紋出現(xiàn),而疲勞裂紋的開閉使材料的非線性出現(xiàn)分散。

4 結(jié)論

研究發(fā)展了一套利用PZT壓電傳感器測(cè)量超聲非線性系數(shù)的實(shí)驗(yàn)系統(tǒng)。利用該系統(tǒng)測(cè)量了AZ31鎂合金拉伸和疲勞試件的超聲非線性系數(shù),實(shí)驗(yàn)結(jié)果表明,超聲非線性系數(shù)對(duì)材料早期力學(xué)性能退化非常敏感。宏觀力學(xué)、非線性超聲檢測(cè)和微觀觀察實(shí)驗(yàn)結(jié)果表明非線性系數(shù) β作為宏觀和微觀的橋梁可以表征材料的力學(xué)性能退化情況。

[1]稅國雙,汪越勝,JIANMIN QU,et al.利用直接激發(fā)Rayleigh表面波的方法測(cè)量材料的聲學(xué)非線性系數(shù)[J].聲學(xué)學(xué)報(bào),2008,33(4)：378-384.

[2]CANTRELL J H.Substructural organization,dislocation plasticity and harmonic generation in cyclically stressed wavy slip metals[J].Proc R Soc Lond A,2004：316-322.

[3]SZILARD J.Ultrasonic testing：non-conventional testing techniques[J].John Wiley＆Sons Ltd,1982.

[4]NAGY P B.Fatigue damage assessment by non linearu ltrasonic materials characterization[J].Ultrasonics,1998, 36：375-381.

[5]JORDAN PM.Finite amp litude acoustic traveling waves in a fluid that saturates a porous medium：Acceleration wave formation[J].Physics Letters A,2006,355(3)：216-221.

[6]JHANG Kyung-Young.Nonlinear ultrasonic techniques for nondestructive assessment ofmicro damage in material：a review.International journal of precision engineering and manufacturing,2009,10(1)：123-135.

[7]CANTRELL JH,YOSTW T.Nonlinear ultrasonic characterization of fatigue microstructures[J].Int.J.Fatigue, 2001,23：S487-S490

[8]BUCK O,ALERSG A.New techniques for detection and monitoring of fatigue damage[J].Fatigue andmicrostructure.American Society for Metals,1979：101-147.

[9]KIM JY,JACOBSL J,QU J,etal.Experimental characterization of fatigue damage in a nickel-base superalloy using nonlinear ultrasonic waves[J].Journal of the Acoustic Society of America,2006,120(3)：1266-1273.

[10]SHUIGuoshuang,KIM Jim-Yeon,QU Jianmin,et al.A-new technique for measuring the acoustic nonlinearity of materials using Rayleigh waves[J].NDT＆E International 2008,41(1)：326-329.

[11]徐從元,姜文華.疲勞金屬材料非線性聲學(xué)特性的試驗(yàn)研究[J].南京大學(xué)學(xué)報(bào),2000,36(3)：328-335.

[12]稅國雙,汪越勝,曲建民.材料力學(xué)性能退化的超聲無損檢測(cè)與評(píng)價(jià)[J].力學(xué)進(jìn)展,2005,35(1)：52-68.

[13]SOHN K Y,JONESJW,BERKMORTEL J,et al.Creep and Bolt Load Retention Behavior of Die Cast Magnesium Alloys for High Temperature App lication[C].SAE Technical Paper Series,20002-012-1120,Warrendale, PA,2000.

[14]胡艷輝,李建國,譚敦強(qiáng),等.細(xì)晶 AZ31鎂合金高溫壓縮變形行為研究[J].航空材料學(xué)報(bào) ,2010,30(1)：36 -40.

[15]BREAZEALE M A,PHILIP Jacob.Determ ination of Third order Elastic Constants from Ultrasonic Harmonic Generation Measurements[C].Physical Acoustics,Vol. 17,Academ ic Press,INC.1984.

[16]CANTRELL J H.Crystalline structure and symmetry dependence of acoustic nonlinearity parameters[J].JApp l Phys,1994,76(6)：3372-3380.

[17]Hurley D C,Fortunko C M.Determination of the non linear ultrasonic parameterβusing a Michelson interferometer [J].Meas Sci Technol,1997,8：634-642.

[18]YOST W T,CANTRELL JH.Materials characterization using acoustic nonlinearity parameters and harmonic generation.Rev.QNDE,1990;9B：1669-1676