鋼筋混凝土框架結構側向倒塌地震易損性分析

呂大剛，于曉輝，陳志恒

(哈爾濱工業大學土木工程學院，150090哈爾濱，ludagang@hit.edu.cn)

控制和預測結構在地震作用下的倒塌是結構設計和評定工作的核心目標.因此，有必要對結構在地震作用下發生倒塌這一動力失穩問題進行深入研究.由于影響結構地震倒塌的因素眾多，且涉及大量不確定性因素，因此倒塌易損性分析成為結構倒塌預測的有效手段.

結構倒塌可以分為豎向(連續)倒塌和側向(增量)倒塌2種.其中，豎向倒塌是由于結構中某一構件由于喪失承載能力退出工作，而引起的結構連續倒塌;側向倒塌則是由于結構側向塑性變形過大而引起的側向承載力喪失.結構在地震作用下的倒塌過程可視為2類倒塌的相繼發生，即:在地震作用下，結構逐漸出現較大的塑性變形，當某一構件的損傷過大，隨即退出工作，進入結構豎向倒塌過程.

側向倒塌作為結構地震倒塌過程的第一階段，是預測和控制結構發生倒塌的關鍵.作為一種動力分析方法，IDA方法可有效解決結構側向倒塌問題.IDA思想早在1977年就由Bertero［1］提出，2000年被美國聯邦緊急事務署(Federal Emergence Management Agency，FEMA)推薦條例FEMA350［2］采用，并作為結構側向倒塌能力分析的重要方法予以推薦，被廣泛應用于結構側向倒塌易損性分析.Zareian和Krawinkler［3-4］同時考慮地震動不確定性和模型不確定性，進行了地震倒塌易損性研究.Liel等［5］在地震倒塌易損性研究中，同時考慮了地震動不確定性和結構不確定性.葉列平和陸新征等［6-7］僅考慮地震動不確定性，利用結構側向倒塌易損性曲線，采用倒塌儲備系數作為評價指標，對結構抗倒塌能力及其影響因素進行了研究.

本文以一棟5層3跨鋼筋混凝土框架結構為例進行側向倒塌地震易損性分析.選擇60條地震動作為輸入，以記錄對記錄(Record-to-record，RTR)的形式考慮地震動的不確定性.基于IDA方法，分別采用FEMA準則和有限元計算失穩作為倒塌能力點的確定原則，分析得到結構側向倒塌易損性曲線.

1 側向倒塌能力點的確定準則

IDA曲線反應了地震動強度參數(Intensity Measure，IM)與結構破壞(反應)參數(Damage Measure，DM)之間的關系.在IDA分析中應保證所選用IM具有單調性，如:峰值加速度(PGA)和譜加速度(Sa)等參數;DM應能較好地表征結構的性能，如:承載力、變形以及損傷等參數.

文獻［8］提出了確定結構側向倒塌能力點的基本原則:以結構發生動力失穩處的IM或DM量值作為結構側向倒塌能力點.根據定義側向倒塌點的參數不同，結構側向倒塌有3種定義準則: DM準則、IM準則和IM-DM準則.

DM準則是以DM量值CDM定義結構側向倒塌能力點，當DM≥CDM時，結構發生倒塌，如圖1所示.我國抗震規范［9］對不同形式結構的塑性極限給出了相應的最大層間位移角限值，可視為采用DM準則進行結構側向倒塌定義.由于結構側向倒塌為動力失穩問題，其主要特征為:在微小外部激勵增長下，結構反應無限增大.因此，圖1出現了同一CDM對應IDA曲線中多個極限點的情況.

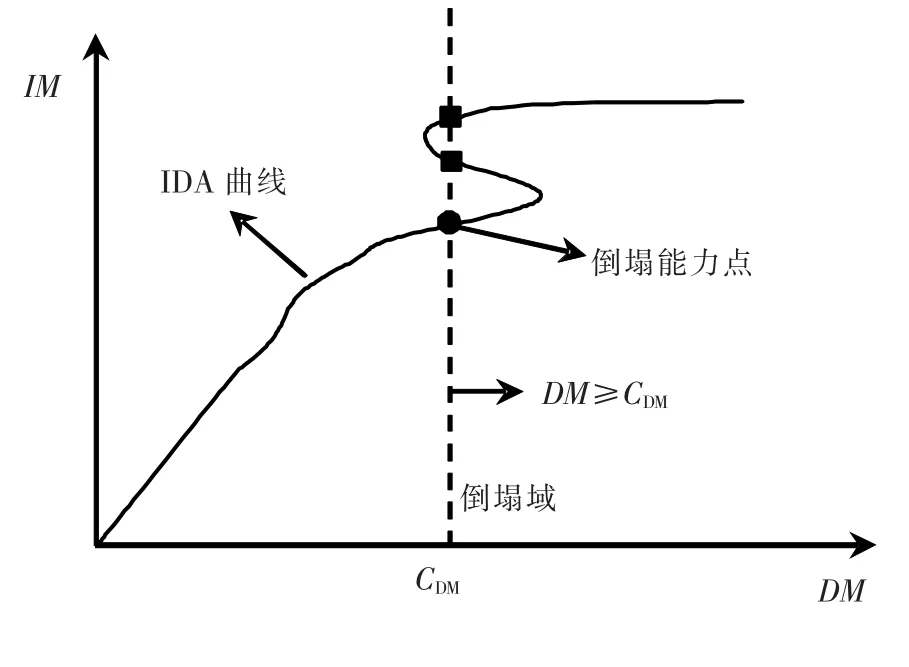
圖1 DM準則確定倒塌能力點

IM準則是用IM量值CIM作為結構側向倒塌能力點，當IM≥CIM時，結構發生倒塌，如圖2所示.IM準則更能描述結構倒塌的特點，如:可采用IDA曲線的平臺段起始點對應的IM值作為CIM.然而采用IM準則定義結構的側向倒塌會出現倒塌點處的DM過大的情況.因此，綜合考慮IM和 DM的兩種測度的IM-DM混合準則是定義結構側向倒塌點的較好方法，即:當 IM≥ CIM或DM≥CDM時，結構發生倒塌.基于IDA曲線，FEMA350［2］建議:當切線剛度退化成初始剛度的20%，或最大層間位移角超過10%時，定義為結構側向倒塌.FEMA原則實際采用的是IM-DM混合原則，如圖3所示.

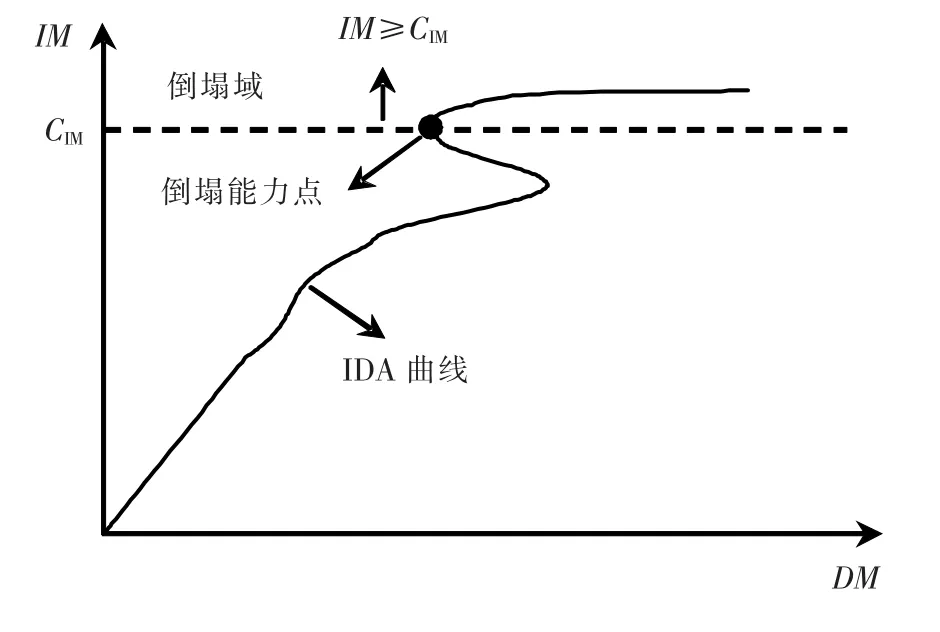
圖2 IM準則確定倒塌能力點

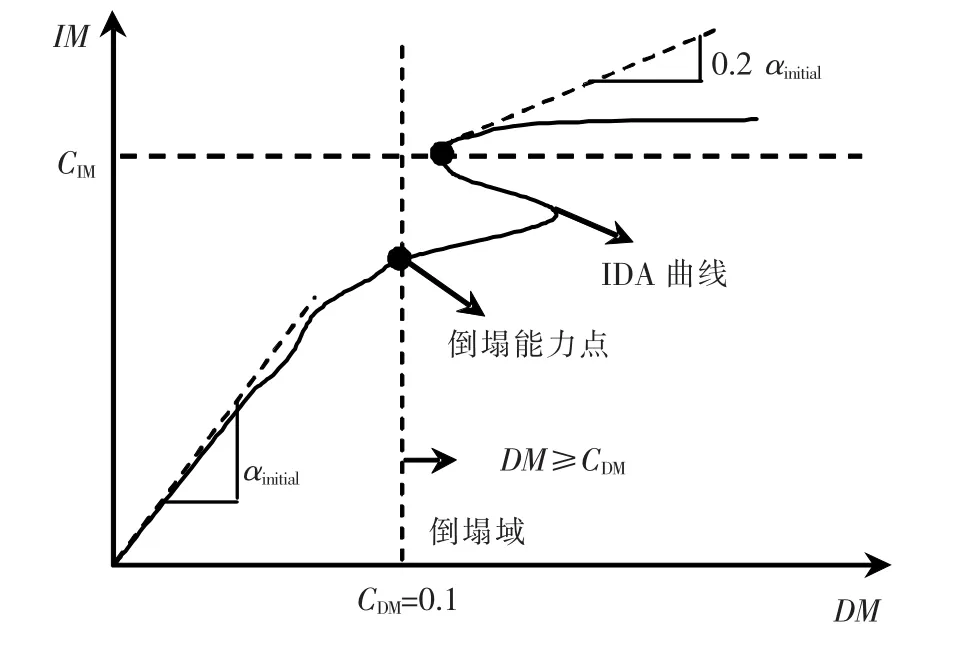
圖3 FEMA準則(IM-DM原則)確定倒塌能力點

本文基于IM原則，曾提出一種“折半取中”方法，通過逼近結構有限元計算失穩點來定義結構側向倒塌［10］.文獻［8］提出了IDA分析中確定調幅系數的Hunt＆Fill原則.其中，Hunt的過程是進行側向倒塌點的搜索階段;Fill的過程是為了保證IDA曲線的光滑，對IDA曲線中間距較大的兩點進行補充分析.本文作者基于OpenSees［11］平臺，實現了Hunt＆Fill過程，如圖4所示.為了保證搜索得到的側向倒塌點具有更高的可信度和穩定性，采用多種求解法則循環進行非線性動力方程的求解，包括:Newton法則、改進的Newton法則以及Broyden法則.若3種法則均無法使有限元分析收斂，則以當前狀態為結構動力失穩，以該點對應的IM量值作為側向倒塌能力點.為進行對比分析，本文同時采用 FEMA350采用的IM-DM原則進行側向倒塌的確定.

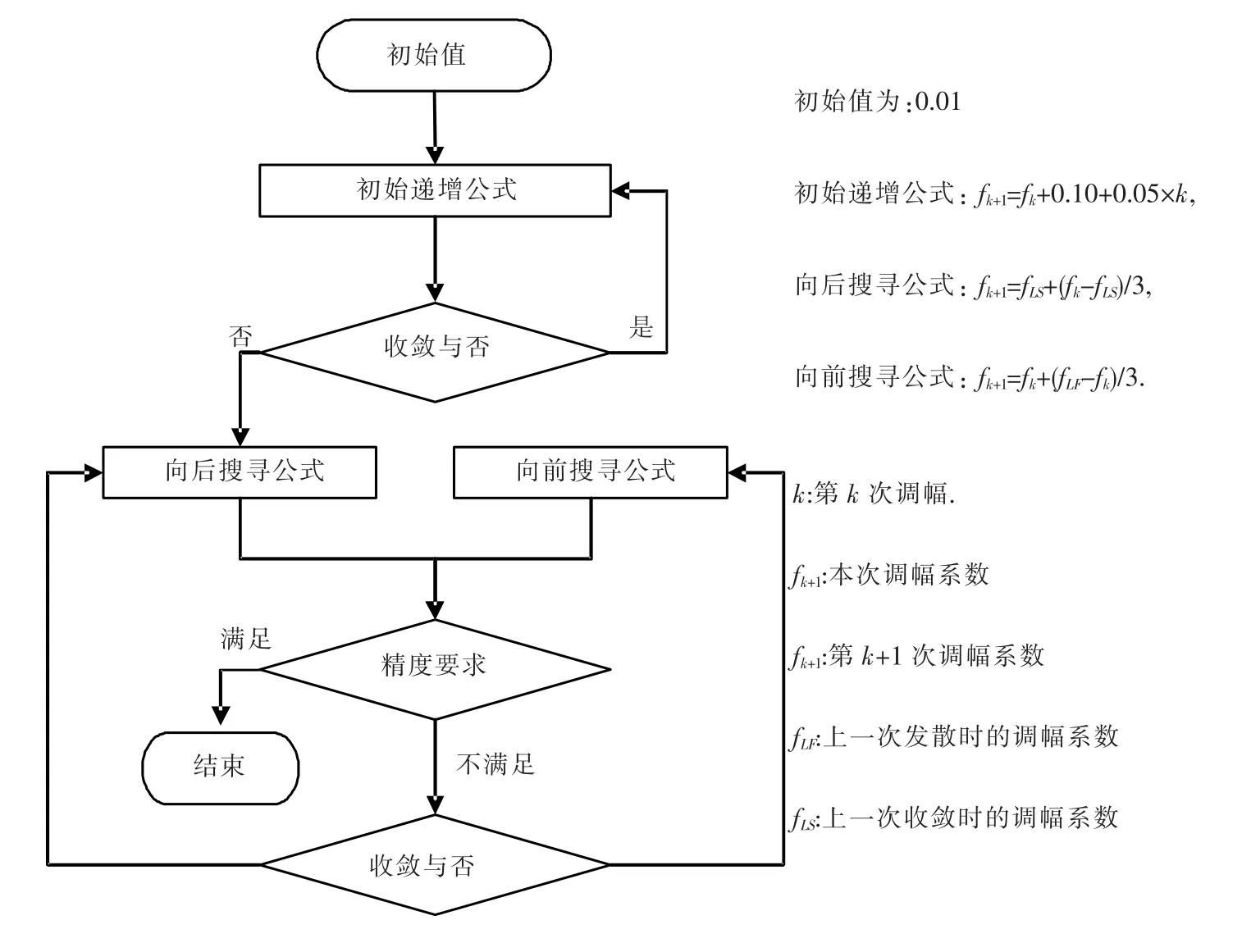
圖4 Hunt＆Fill的分析流程

2 結構側向倒塌地震易損性

地震動選擇的不同會造成結構IDA分析結果的較大差異，這體現了地震動不確定性對IDA分析結果的影響.因此，在結構側向倒塌研究中，常常考慮地震動的不確定性，采用側向倒塌易損性作為描述結構抗倒塌能力的工具.研究表明［8］:采用譜加速度Sa作為IM可以有效地刻畫結構側向倒塌，并減少地震動不確定性對IDA分析結果的影響.

結構側向倒塌易損性表征的是結構在不同地震動強度下，發生側向倒塌的失效概率: P［Collapse|Sa=x］.文獻［3-4］采用對數正態分布函數對結構側向倒塌易損性進行研究.

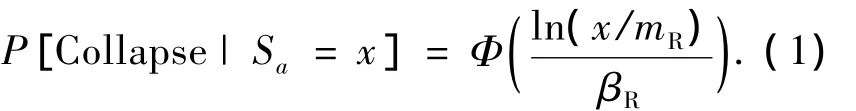
式中mR和βR為易損性函數參數.

本文采用統計的方法進行結構側向倒塌地震易損性分析.

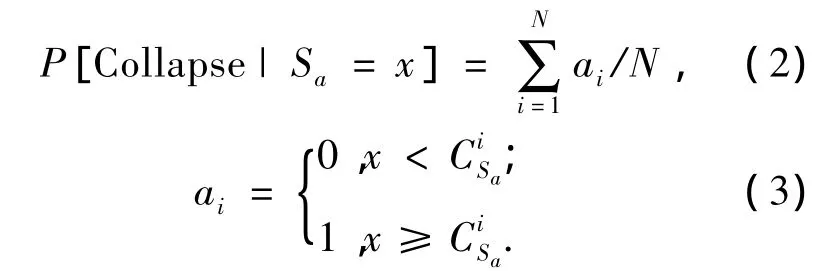
采用統計的方法進行結構側向倒塌易損性分析，可采用如下步驟:

1)從地震動記錄數據庫中(例如PEER的數據庫)選擇N條地震動記錄;

2)建立結構的非線性有限元模型;

4)按式(2)確定結構倒塌概率P［Collapse|Sa=x］;

5)在合理的范圍內增量式地遍取Sa=x，獲取結構側向倒塌概率的離散數據點;

6)利用步驟(5)中獲得的離散數據點，采用最小二乘法或極大似然法對式(1)進行擬合，并估計倒塌易損性函數參數mR和βR.

3 算例分析

5層3跨鋼筋混凝土框架結構，8度設防，設計基本加速度為0.2 g，場地土為Ⅱ類.結構平面布置、立面尺寸及典型梁柱截面配筋情況，見圖5.基于OpenSees分析平臺，梁和柱采用基于位移的非線性纖維梁-柱單元模擬.混凝土采用Concrete01材料，鋼筋采用Steel02材料.綜合考慮計算精度和效率，梁構件設置5個積分點，柱構件設置10個積分點.柱截面考慮縱向鋼筋和箍筋對核心混凝土的軸向承載能力的加強，采用Mander約束混凝土本構模型對核心混凝土進行模擬［12］.

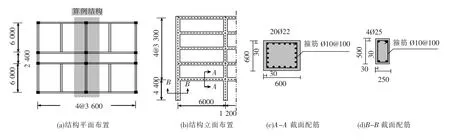
圖5 算例結構平面和立面布置及典型梁柱配筋(mm)

考慮場地類型與地震動分組，根據地震動特征周期選取了60條距離震中10 km以上的地震，地震動列表見文獻［13］.選取結構第一周期對應的譜加速度為IM，分析得到60條IDA曲線.基于FEMA原則，確定60個結構倒塌能力點，見圖6.基于Hunt＆Fill原則逼近結構有限元分析發散點，確定60個結構倒塌能力點，見圖7.

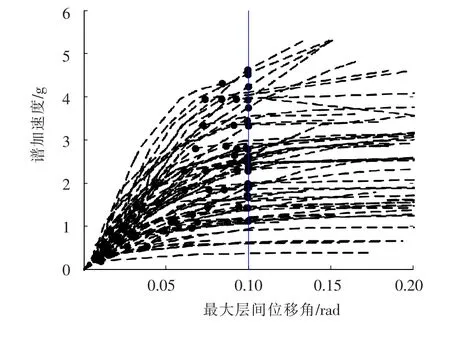
圖6 基于FEMA原則的側向倒塌能力點

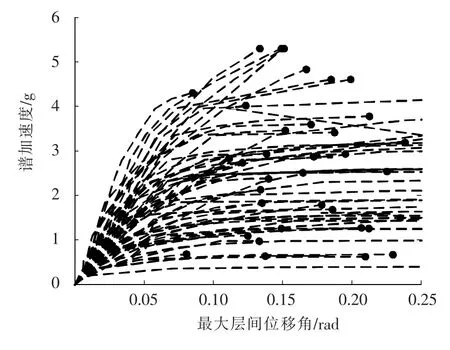
圖7 基于有限元分析失穩原則的側向倒塌能力點

從圖6可見，當鋼筋混凝土結構達到這些控制點時，IDA曲線已經呈現出較為明顯的水平段，說明采用FEMA原則進行結構側向倒塌能力點的確定，可以較好地表征結構側向倒塌的動力失穩特性.

利用式(2)得到了結構基于不同準則的倒塌易損性數據點，進一步采用最小二乘法對這些離散點進行式(1)的擬合，獲得連續的側向倒塌易損性曲線，如圖8所示.

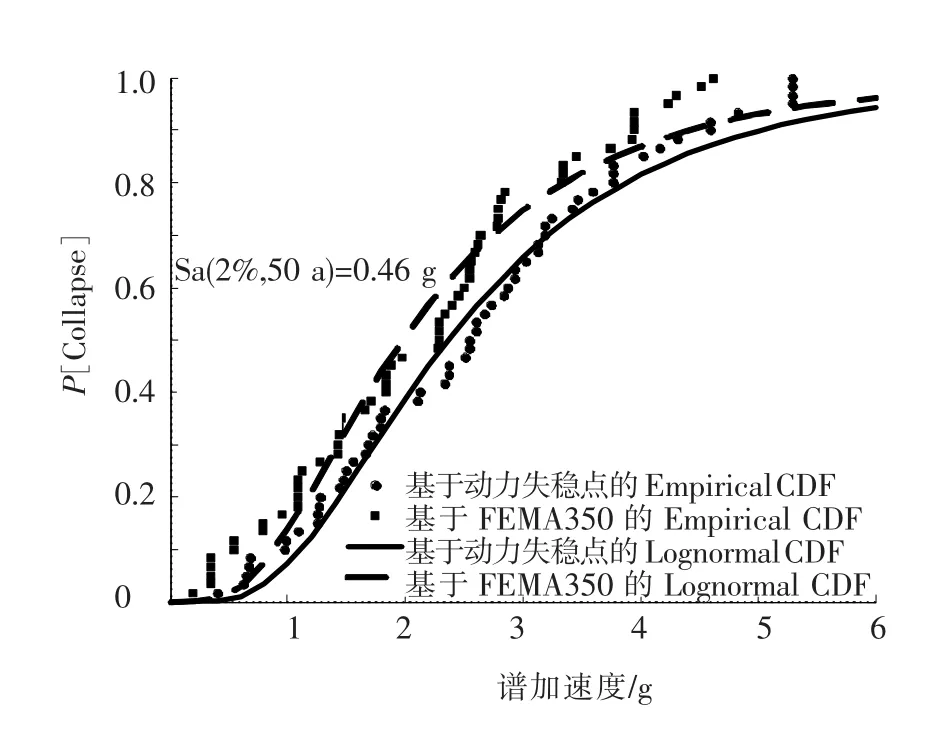
圖8 結構側向倒塌易損性曲線

由圖8可見，當結構采用FEMA原則確定倒塌能力點時，結構倒塌能力中位值mR=1.90 g，對數標準差為βR=0.64 g，結構在大震作用下(Sa (2%，50 a))發生倒塌的概率為1.32%.當采用計算發散點作為控制準則時，結構的倒塌能力中位值mR=2.32 g，對數標準差為βR=0.60 g，罕遇地震水平下結構發生倒塌的概率為0.35%.由此可知:

1)基于FEMA的確定結構側向倒塌能力點的方法相對保守，可較為有效地對結構的側向倒塌風險進行控制;

2)我國規范的大震作用下，結構發生倒塌的風險較小.按其進行結構設計，可有效地控制結構側向倒塌風險，但不能完全釋放結構抵抗倒塌的能力，會造成結構設計的浪費.

4 結語

以一棟5層3跨鋼筋混凝土框架結構為例進行側向倒塌易損性分析.選擇60條遠場II類場地的地震動作為輸入，分別采用FEMA倒塌能力點確定原則，和基于有限元計算失穩的倒塌能力點確定原則，分析得到結構的側向倒塌地震易損性曲線.研究表明:結構側向倒塌易損性可有效刻畫結構在不同強度地震動作用下，發生倒塌的危險.FEMA350和我國規范對倒塌能力點的確定原則均相對保守，可較為有效地對結構的側向倒塌風險進行控制，但無法完全釋放結構抵抗倒塌的能力.

［1］BERTERO V V.Stength and deformation capacities of buildings under extreme environments［C］//PISTER K S.Structural Engineering and Structural Mechanics. Prentice-Hall:Englewood Cliffs，1977:211-255.

［2］Federal Emergency Management Agency.Recommended seismic design criteria for new steel moment-frame buildings，FEMA350［R］.Washington，DC:Federal Emergency Management Agency，2000.

［3］ZAREIAN F.Simplified performance-based earthquake engineering［D］.San Francisco:Stanford University，2006.

［4］ZAREIAN F，KRAWINKLER H.Assessment of probability of collapse and design for collapse safety［J］. Earthquake Engineering and StructuralDynamics，2007，36(13):1901-1914.

［5］LIEL A B，HASELTON C B，DEIERLEIN G G，et al. Incorporating modeling uncertainties in the assessment of seismic collapse risk of buildings［J］.Structural Safety，2009，31(2):197-211.

［6］陸新征，葉列平.基于IDA的結構抗地震倒塌能力研究［J］.工程抗震與加固改造，2010，32(1):13-18.

［7］唐代遠，陸新征，葉列平，等.柱軸壓比對我國RC框架結構抗地震倒塌能力的影響［C］//北京市建筑設計研究院.第十二屆高層建筑抗震技術交流會論文集.北京:中國建筑學會抗震防災分會，高層建筑抗震專業委員會，2009:35-45.

［8］VAMVATSIKOS D，CORNELL C A.Incremental dynamic analysis［J］.Earthquake Engineering and Structural Dynamics，2002，31(3):491-514.

［9］GB 50011—2001建筑抗震設計規范［S］.北京:中國建筑工業出版社，2001.

［10］呂大剛，于曉輝，王光遠.基于單地震動記錄IDA方法的結構倒塌分析［J］.地震工程與工程振動，2009，29(6):33-39.

［11］MCKENNA F，FENVES G L，SCOTT M H.Open system for earthquake engineering simulation［R］.University of California at Berkeley:Pacific Earthquake Engineering Research Center，2008.

［12］MANDER J B，PRIESTLEY M J，PARK R.Theoretical stress-strain model for confined concrete［J］. ASCE/Journal of Structural Engineering，1988，114 (8):1804-1826.

［13］陳志恒.鋼筋混凝土框架結構的倒塌失效模式、風險與魯棒性分析［D］.哈爾濱:哈爾濱工業大學，2009.