非線性相關的失效數據聯合聚類分析與預測

盧 旭，王慧強，呂 曉，馮光升，林俊宇

(1.哈爾濱工程大學計算機科學與技術學院，150001哈爾濱，luxu-hrbeu@yahoo.cn; 2.海軍工程大學電子工程學院，430033武漢)

隨著高性能計算機系統應用的日益普及和對其高可用性的嚴格約束，如何預測并避免系統可能的失效成為當前一個研究熱點［1-2］.實現失效預測首先需要對系統所生成的大規模失效數據進行分析，其研究關鍵就是將具有相似失效模式的失效樣本聚集在一起，為后續失效預測與快速恢復提供決策依據.失效數據對象間的一個重要關系就是非線性相關性［3］，可用以反映特征向量之間的依賴性或者關聯關系，隨著近年高性能計算系統失效數據的對外開放［4-5］，此類失效數據分析和預測問題的研究逐漸引起了廣泛關注.

目前對系統失效數據的分析主要有:1)分析系統運行歷史記錄，計算失效平均間隔時間; 2)提取失效事件時序特征，通過辨別系統失效模式預測失效.這2類方法盡管在各自的系統上表現優異，但沒有有機融合失效特征進行綜合評判，或者對于冗余、重復數據需要人為進行篩選，難以得到推廣［6-7］.在分布式、高性能計算機系統中，失效數據往往具有稀疏、髙維等特征，且有價值的非線性相關性主要存在于維度子空間內，而此類單向聚類方法難以發現這些維度子空間內的局部相關性，增加了失效預測的不確定性.本文分析失效特征的非線性相關性，引入聯合聚類思想(Coclustering)［8］，以互信息熵損失差作為聯合聚類度量標準，提出非線性相關失效數據聯合聚類算法，實現非線性相關失效數據自動分析與預測.

1 失效預測基本模型

1.1 失效預測框架

盡管目前已經研究出多種容錯機制，致力于避免故障發生后導致系統服務中斷，但在實際應用中失效的發生總是不可避免，因此要保證系統的高可用性就必須為系統提供失效預測的能力.根據預測時間的長短，失效預測可分為長期預測和短期預測，其中:長期預測大多通過分析系統可靠性模型來獲得失效事件的季節性分布;短期失效則通過失效事件的關聯性來預見可能發生的失效，失效預測框架如圖1所示.在t時刻預測在t+Δt時間段內是否發生失效，其中:Δt為預先時間;Δtw為Δt的下限表示的失效預恢復所需時間;Δtp為預測期，描述了整個預測時間窗口的長度.顯然，預測時間窗口越長，則時間窗口內發生失效的可能性越大.

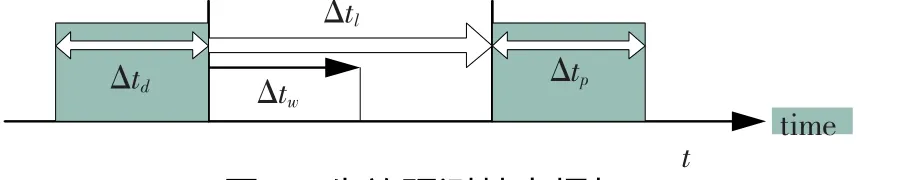
圖1 失效預測基本框架

1.2 失效特征相關性分析

對大規模失效數據集的分析首先需要從運行系統中提取出能夠反映與失效事件關聯的系統狀態特征.這些特征應當能夠表示出系統在正常執行時與失效事件發生時的差異，同時還需要捕捉到不同失效事件中間的時空關聯性.失效特征應該能夠反映系統失效與正常運行下的本質區別，同時還需要能夠反映失效事件的時空關聯性.一般而言，特征空間可分為強相關特征、弱相關特征和無關特征［9］.設F是特征集合，fi是一個特征，Si=F-{fi}，特征相關性的形式化定義為:

定義1 特征fi是強相關的當且僅當P(C|fi，Si)≠P(C|Si).

定義2 特征fi是弱相關的當且僅當P(C|fi，Si)=P(C|Si)，且存在S'i?Si，使得P(C|fi，S'i)≠P(C|S'i)強相關特征是對類的分布構成影響的特征，弱相關特征則只在一定條件下影響不同類之間的分布，以此為基礎可給出失效特征非線性相關性定義.

定義3 特征fi是非線性相關的當且僅當特征是強相關或弱相關，且ρ=0為

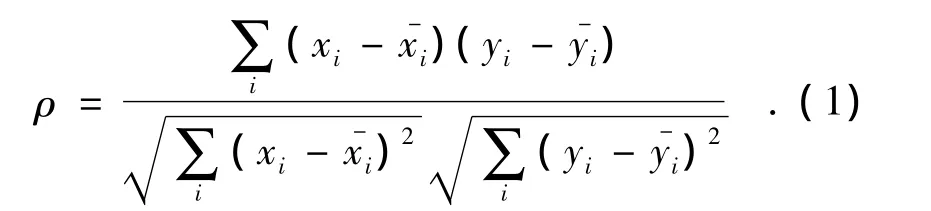
式中ρ被稱為線性相關系數且x，y∈F.

通過比對系統各部分失效發生的關聯性，給出用于失效預測特征提取的性能指標.這些指標可從系統事件日志中提取，例如處理器與存儲空間利用率，通訊與輸入輸出操作的容量等.而固定時間窗口內的失效事件數、失效類型與平均失效間隔時間等則用來構建系統失效的統計模型.

定義4 失效特征標簽由七元組給出定義: tuple(fID，time，fLoct，fType，usrUtil，pktCount，io-Count).其中:fID，time，fLoct，fType分別為失效事件編號、時間戳、失效定位和失效類型;usrUtil為系統失效時資源利用率;pktCount，ioCount分別為衡量特征提取階段的數據包與通信請求數.

2 失效數據聚類方法

基于信息論的聯合聚類算方法從數據矩陣行維與列維2個方向上聚類，在數據分析、協同過濾等研究領域有著廣泛應用［10］.假設m個待聚類失效樣本，記作{x1，x2，…，xm};若每個失效事件特征標簽用n維特征向量Y描述，記作{y1，y2，…，yn}. p(X，Y)為隨機變量X和Y的聯合概率分布，由于X和Y都是離散型隨機變量，p(X，Y)可以用一個m×n矩陣表示，矩陣中每個元素p(x，y)表示失效事件x和失效特征標簽y聯合發生的概率.

定義5 聯合聚類映射定義為

式中:隨機變量^X，^Y分別為聯合聚類后失效事件與特征標簽集合;k，l分別為聯合聚類后失效事件簇和失效特征簇的數量.

聯合聚類映射可簡寫為^X=CX(X)和^Y= CY(Y).文獻［8］引入了互信息熵(mutual information)的概念對聯合聚類問題進行量化分析，并給出了聯合聚類映射函數的最優解形式.

定義6 最優聯合聚類應滿足聚類前后的互信息熵差最小化計算為

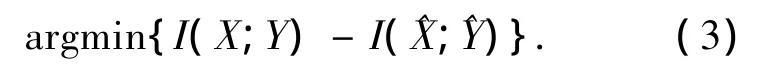
其中:互信息熵計算為

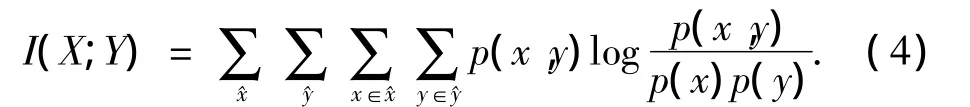
式中:D(·‖·)為KL散度，或稱為相關熵;q(x，y)=.在求解聯合聚類算法的映射函數時，KL散度度量被進一步表述為2種對稱形式，用于實現行聚類和列聚類，計算公式分別為

在上述分析基礎上，提出非線性相關的失效數據聯合聚類分析算法.算法分3個部分:1)根據已知的失效事件與特征標簽聯合分布進行初始化，并給出初始化映射函數;2)按照互信息熵差計算方法分別進行行聚類和列聚類，最終獲得新的聯合聚類子集;3)判斷聯合聚類后的數據矩陣是否滿足終止條件，如果不滿足則繼續進行聚類迭代直至滿足收斂條件為止.算法詳細步驟如圖2所示.

圖2 非線性相關失效數據聯合聚類算法

由于非線性相關的失效數據聯合聚類分析很難在可接受的時間內獲得最優的聚類結果，因此當互信息熵差小于某一給定任意小整數時，可近似認為聯合聚類達到局部最優.為確保算法能在有限事件內獲得聯合聚類結果，還需要保證失效數據聯合聚類算法能夠在有限迭代次數后收斂.

引理1 非線性相關失效數據聯合聚類算法總能在有限次迭代后收斂并達到局部最優.

證明 KL散度可通過下式進行分解，即

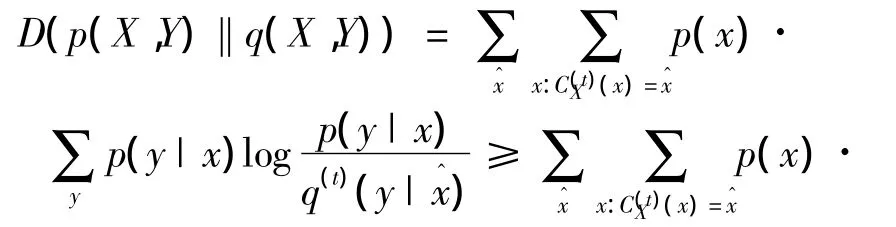
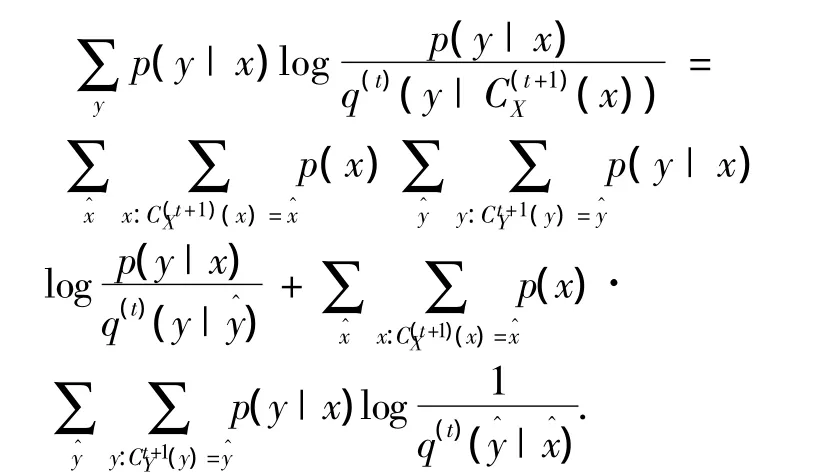
而由于

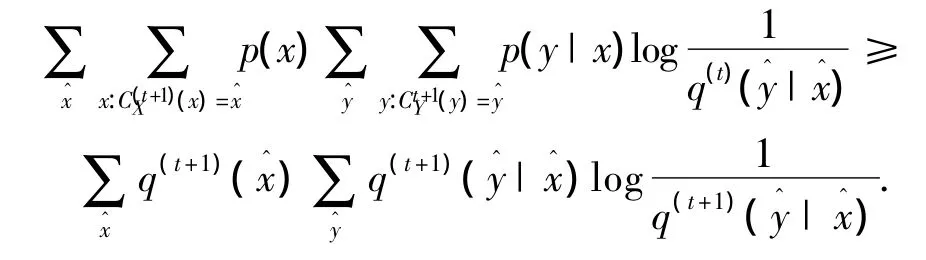
因此有

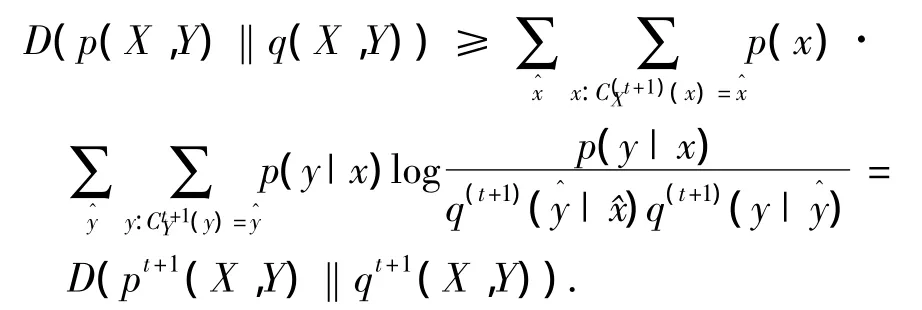
由于每次迭代后行簇與列簇的數目是有限的，且任意小整數ε確定，所以非線性相關的失效數據聯合聚類算法總能在有限次迭代后收斂且達到局部最優，證明完畢.

3 實驗結果與分析

3.1 失效特征提取

實驗采用了美國洛斯阿拉莫斯國家實驗室(Los Alamos National Laboratory，LANL)22臺高性能計算系統從1996～2005年的運行記錄作為失效數據來源［5］.LANL高性能計算系統采用獨立內存接口以及多級處理器結構，共包含4 750個節點以及24 101個處理器，LANL高性能計算機系統在規模、體系結構等方面均呈現出多樣性，大部分工作負載為3D仿真和可視化計算.圖3分別顯示了 LANL高性能計算機系統從2003年9月1日～2005年8月31日CPU失效、內存失效、應用程序失效和文件系統失效4種類型的時間分布.由圖3可知，不同的失效類型具有不同的時間分布特征，在聯合聚類分析時必須根據不同類型失效的特征分布進行區分.

3.2 聯合聚類性能測試

實驗給出了失效數據聯合聚類算法在LANL失效數據集上運行的收斂速度和聚類效果，同時引入迭代雙聚類算法(Iterative Double Clustering，IDC)［11］以及失效數據聚類的temporal和spatial算法進行比較.算法在Window XP平臺上實現，硬件環境為Intel Celeron CPU 2.4 GHz，主存1 G.實驗采用LANL實驗室高性能計算機2004年6月～2005年9月之間的失效數據作為聚類算法性能測試的數據來源.

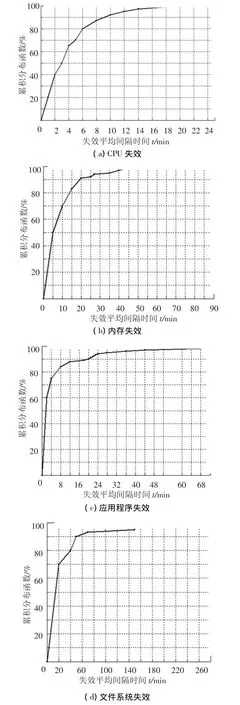
圖3 4種失效類型時間分布

實驗首先考察4類算法在不同數據規模下的運行時間.圖4為失效數據矩陣的列數固定時算法運行時間和數據行數的關系曲線，分別測試矩陣行數m分別從1 000～3 000之間變化的運行時間.圖5為失效數據矩陣的行數固定時算法運行時間與矩陣維數的關系曲線，分別測試維數從5～25的運行時間.聚類分析時間隨著失效樣本數的增加而遞增，其中temporal和spatial算法耗時最短，而迭代雙聚類以及本文所提算法耗時較長，這是因為前者屬于單維聚類方法，在聚類相似度計算時僅考慮行聚類問題，而后者則從行聚類以及列聚類2方面進行聚類計算，因此算法運行時間不可避免地延長.

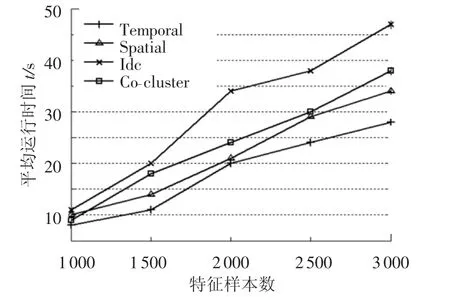
圖4 列數固定時算法運行時間與行數關系曲線

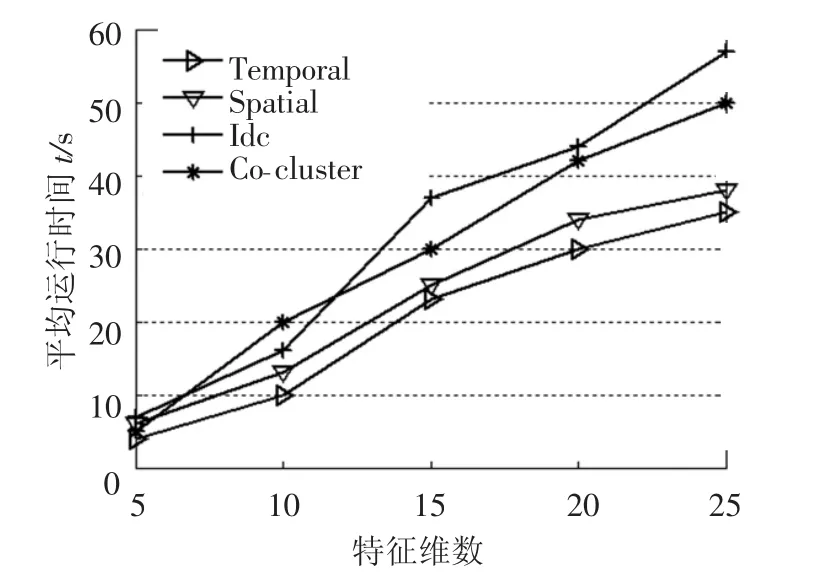
圖5 行數固定時運行時間與列數關系曲線

圖6表示在聚類過程中互信息熵差與算法運行時間的曲線關系.由圖6可知，聚類過程中互信息熵差隨著聚類算法運行時間遞減，在算法運行初始階段，2類聯合聚類算法熵差達到最大值，在聚類分析10 s后開始平滑下降.圖7為聚類過程中算法迭代次數與運行時間的曲線關系.由圖7可知，從聚類初始階段開始，當算法運行超過30 s后，迭代也超過50次/s且逐步達到最大值.

為評測聚類算法用于失效預測的有效性，根據標注的LANL實驗室失效數據真實類別計算聚類結果的查準率(precision)和查全率(recall)，如表1所示.表1的數據表明，2種聯合聚類算法的聚類結果中4類失效類型的查準率均高于65%.這是因為本文所提算法在單次行聚類或列聚類時均按照KL散度計算信息熵損失.作為對比，單維聚類算法由于僅按照時間分布或空間分布2種特征進行聚類，因此對于4種失效類型的聚類分析結果均不盡理想.對聚類過程中互信息熵差與迭代次數的考察說明，聯合聚類算法能有效考慮不同特征的關聯性，并采用關聯特征來度量失效事件間相似性，因此聯合聚類較單維聚類效果更好.

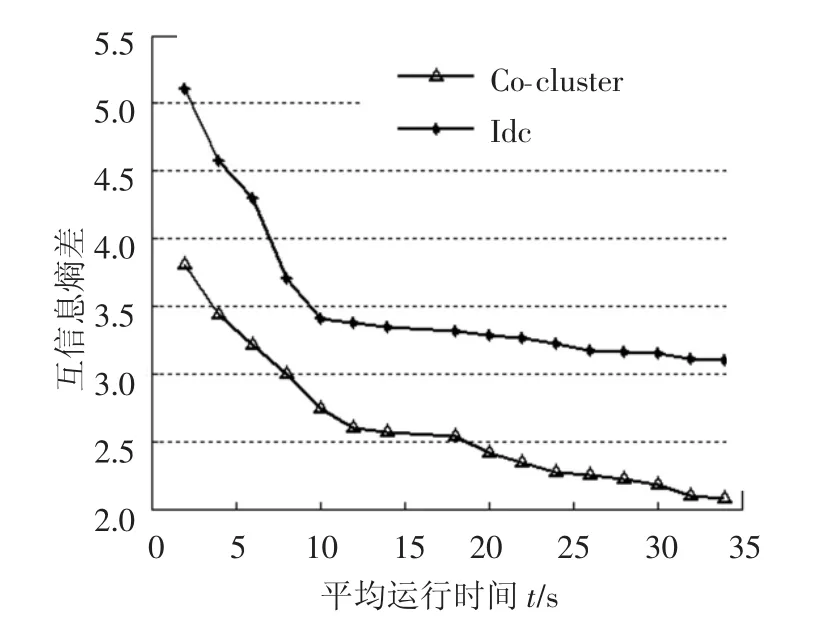
圖6 互信息熵差與運行時間的關系曲線

圖7 算法迭代次數與運行時間的關系曲線

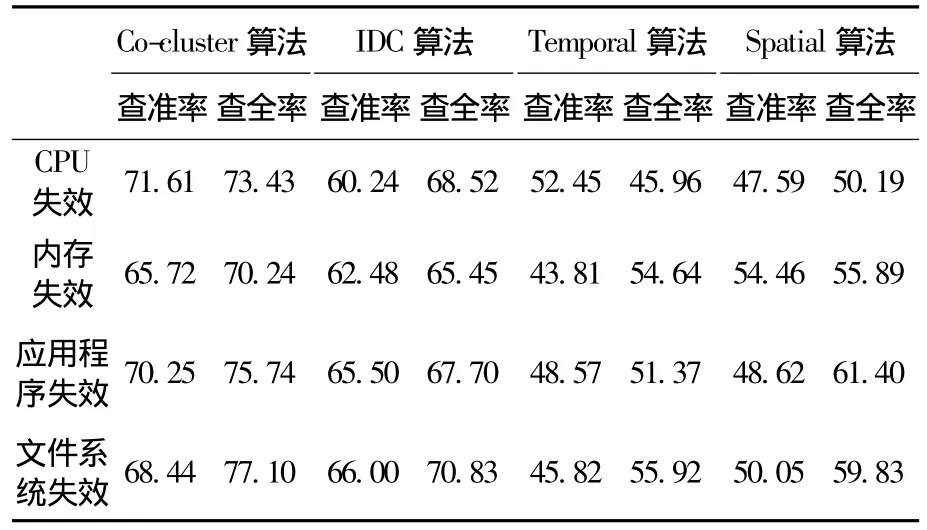
表1 聚類算法實驗結果比較 %

4 結論

1)針對高性能計算機系統非線性相關失效數據的髙維、稀疏等特征，提出非線性相關失效數據聯合聚類算法，以互信息熵損失差作為聯合聚類度量標準并闡明了算法在有限次迭代后的收斂性.

2)實驗計算了4種常見失效類型的時間分布，并比較了不同算法在失效數據集上的聚類效果和收斂速度.實驗結果表明，本文所提出的非線性相關失效數據聯合在聚類準確性、聚類計算時間耗費等方面優于單向聚類方法.

［1］KEPHART J O，CHESS D M.The vision of autonomic computing［J］.IEEE Journal of Computer，2003，36(1):41-50.

［2］SOLANO-QUINDE L D，BODE B M.Module prototype for online failure prediction for the IBM BlueGene/L［C］//IEEE International Conference on Elector/Information Technology.Ames:IEEE Computer and Communication society，2008:470-474.

［3］FU Song，XU Chengzhong.Exploring event correlation for failure prediction in coalitions of clusters［C］//Proceedings of the 2007 ACM/IEEE Conference on Supercomputing.New York，NY:ACM，2007:456-468.

［4］OLINER A，STEARLEY J.What supercomputers say: A study of five system logs［C］//Proceedings of the 37thAnnual IEEE/IFIP International Conference on Dependable Systems and Networks.Washington，DC:IEEE Computer Society，2007:575-584.

［5］SCHROEDER B，GIBSON G A.A large-scale study of failures in high-performance computing systems［C］// Proceedings of the International Conference on Dependable Systems and Networks.Washington，DC:IEEE Computer Society，2006:249-258.

［6］LIANG Y L，ZHANG Y Y，SIVASUBRAMANIAM A A，et al.BlueGene/L failure analysis and prediction models［C］//Proceedings of the International Conference on Dependable Systems and Networks.Washington，DC:IEEE Computer Society，2006:425-434.

［7］LIANG Y L，SIVASUBRAMANIAM A，MOREIRA J. Filtering failure logs for a BlueGene/L prototype［C］// Proceedings of the 2005 International Conference on Dependable Systems and Networks.Washington，DC: IEEE Computer Society，2005:476-485.

［8］DHILLON I S，GUAN Y Q.Information theoretic clustering of sparse cooccurrence data［C］//Proceedings of the Third IEEE International Conference on Data Mining.Washington，DC:IEEE Computer Society，2003: 517-520.

［9］JOHN G H，KOHAVI R，PFLEGER K.Irrelevant feature and the subset selection problem［C］//Proceedings of the 11th International Conference on Machine Learning.San Francesco:Morgan Kaufmann，1994:121-129.

［10］閆雷鳴，孫志揮，吳英杰，等.聯合聚類非線性相關的基因表達數據［J］.計算機研究與發展，2008，45(11): 1865-1873.

［11］EL-YANIV R，SOUROUJON O.Iterative double clustering forunsupervised and semi-supervised learning［C］//Proceedings of the 12thEuropean Conference on MachineLearning. London，UK:Springer-Verlag，2001:121-132.