用離散粒子群優化算法求解WTA問題

曲在濱，劉彥君，徐曉飛

(1.哈爾濱工業大學計算機科學與技術學院，150001哈爾濱，zbqu@hotmail.com; 2.哈爾濱理工大學計算機科學與技術學院，150080哈爾濱)

武器-目標分配(Weapon-target Assignment，WTA)問題是現代戰爭中一個十分重要的問題，其解空間隨武器種類數和目標總數的增加而呈指數級的增加，使其成為一個多參數、多約束NP完全問題［1-2］.對于WTA問題，國內外主流的求解方法多采用諸如神經網絡、遺傳算法、模擬退火算法和蟻群優化等求次優解方法，但它們的求解效率都還不是十分令人滿意，所以探索有效的求解方法解決WTA問題仍然十分重要.

目前，關于單一兵器火力分配問題的文獻已比較多，然而由于在現代作戰中，經常是多種類型的兵器聯合作戰，故需對多種不同類型的兵器的武器-目標分配問題進行探討.文獻［3-6］雖然解決的是多種武器類型的火力分配問題，但所建立模型還是一種簡化模型，在實際使用中一般需添加額外約束條件，如對各目標分配的武器數目限制等.本文針對多類型兵器的火力分配問題給出更實用的數學模型，并將粒子群算法求解問題的思路應用于此問題，用實例驗證了方法的可行性及有效性.

1 問題的描述

具體問題可描述為:設有n個目標;m種類型武器;Vj為目標j的威脅度;Wi為可分配給目標的i類型武器數量;pij為i類型的一個武器對目標j的殺傷概率;xij為給目標j分配i類型武器的數量，目標j最多可分配武器數量為Nj.WTA問題是要確定分配給各目標的各類武器數量以使所有目標的總期望生存值最小，這個問題可形式化為

xij≥0且為整數，i=1，2，…，m，j=1，2，…，n.式中qij=1-pij，即目標j受到一發i類型武器打擊的生存概率.

2 粒子群優化算法

粒子群優化Particle Swarm Optimization(PSO)算法是由Kennedy等［7］在1995年提出的，此算法受鳥群覓食行為的啟發，并用于解決優化問題.同遺傳算法相比，PSO算法不但具有遺傳算法的全局尋優能力，還具有較強的局部尋優能力.

算法將每個個體看作是在n維搜索空間中的一個沒有重量和體積的粒子，并在搜索空間中以一定的速度飛行.每個粒子的飛行速度根據其本身的飛行經驗和群體的飛行經驗不斷調整.每個粒子代表解空間的一個候選解，解的優劣程度由適應函數決定，而適應函數根據優化目標定義. PSO隨機初始化一群粒子，其中第i個粒子在n維解空間的位置為xi=(xi1，xi2，…，xin).粒子通過在每一次迭代中動態跟蹤2個極值來更新其速度和位置為:

1)粒子本身從初始到當前迭代搜索產生的最優解:個體極值pi=(pi1，pi2，…，pin);

2)整個粒子種群目前的最優解:全局極值pg=(pg1，pg2，…，pgn).

如果第i個粒子的速度表示為vi=(vi1，vi2，…，vin)，粒子根據式(1)，式(2)來動態調節自己的“飛行”，得到搜索問題的最優解為

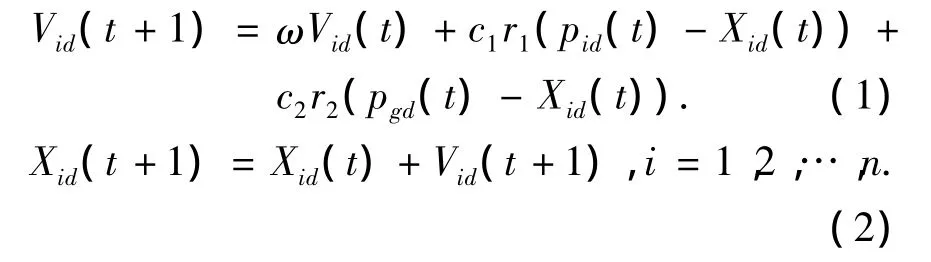
式中:t為迭代次數;c1，c2分別為正常數，稱為學習因子，一般有c1=c2=2;r1，r2分別為(0，1)之間的隨機數;ω為慣性因子.

3 離散PSO算法求解WTA問題

3.1 約束處理方法

WTA問題的解可表示為一個矩陣 X= (xij)m×n，其中xij為第i類武器分配給第j個目標的數目.在這里，每個粒子的位置便對應著武器的一種分配方案.對粒子群迭代中產生的不可行解采用修正結果值方案的方法進行修正，使其在可行解空間范圍內搜索.具體實現時利用一個可行性函數檢查新產生的解是否滿足所有約束.當不滿足時，采用啟發式策略進行調節.調節策略為:

1)如果分配方案中某一目標的武器分配總數超過約束限制，則取消對此目標殺傷概率最小的超出數目的武器分配;如果此種武器分配數少于超出數目，則需取消此種武器的全部分配.重復步驟1)，直到各目標滿足各自的武器分配總數約束.

2)如果分配方案中某種武器的分配不滿足約束，則在已分配這種武器的目標中選擇“威脅度與此種武器對此目標殺傷概率之和”最小的目標，取消超出單位數的武器分配;如果超出單位數大于分給此目標的武器數，則余下部分再從占用此種武器且滿足選擇準則的目標中取消分配.重復步驟2)，直到各種武器分配滿足約束為止.

本啟發式策略運用了貪心思想，盡可能使所做調節有利于提高武器對目標打擊的有效性，從而加速找到最優或次優的分配方案.

3.2 離散PSO算法實現

本文對粒子群算法中的速度和位置進行了重新定義.對速度進行的重新定義為

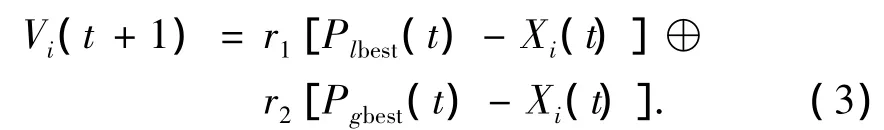
式中:r1［Plbest(t)-Xi(t)］為第i個粒子的位置Xi的任一列以概率r1與其個體極值Plbest(t)的對應列做減法運算，未做減法運算的列一律清零; r2［Pgbest(t)-Xi(t)］為第i個粒子的位置Xi的任一列以概率r2與全局極值Pgbest(t)的對應列做減法運算，未做減法運算的列一律清零;⊕為對作為操作數的2個矩陣產生1個新的矩陣，當2個操作數矩陣的對應列所有元素均為0，則結果矩陣的相應列也為全0;如果只有一列不全為0，則此列為結果矩陣的對應列;否則任選其中一列為結果矩陣的對應列.

上述定義解決了速度難于表示問題，而進行位置的更新為

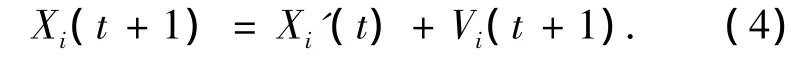
式中:Xi'(t)為將Xi(t)隨機選擇一行根據相應類型武器數目對各目標產生隨機分配而其余各行保持不變的結果，而“+”運算則為2個矩陣對應元素相加.

求解WTA問題的離散PSO算法(DPSOWTA)描述為:

1)初始化粒子群，即隨機設定各粒子的初始位置X和速度V;

2)計算每個粒子的個體適應度值(即目標函數值);

3)將每個粒子的適應度值與個體極值Plbest比較，若更好，則更新Plbest;

4)將每個粒子的適應度值與全局極值Pgbest比較，若更好，則更新Pgbest;

5)根據式(3)和式(4)更新粒子的速度和位置，并使用啟發式策略調整新位置;

6)如未達到最大的迭代次數，則返回步驟2);否則結束.

算法在對每一粒子初始化時根據各類武器的數目隨機產生分配方案，且使其滿足各約束條件.

4 算法測試

假設有6個目標，T1，T2，…，T6，各目標的威脅度如表1所示.5種武器:W1，W2，W3，W4，W5的數目為{4，3，3，2，2}，對各目標最多可使用武器數目為{1，1，2，1，1，2}，各類武器對各目標的單發殺傷概率如表2所示.

表1 各目標的威脅性系數

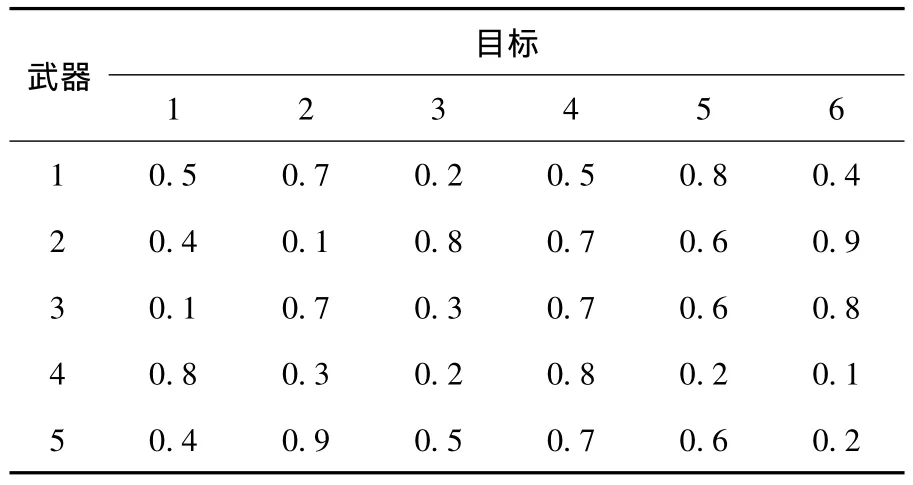
表2 武器對目標的殺傷概率表

算法具體實現時，為避免陷入局部最優，若全局極值在進化一定代數后保持不變，則只保留最優粒子，其他粒子全部重新生成.本例中的粒子數取為30，最大迭代數為100.在P4 1.7 G/512 M微機上重復執行算法50次得出的最優方案的適應度值情況如表3所示，最優分配方案的適應度函數值為0.634，與枚舉算法所得分配方案的適應度函數值相同.

表3 最優方案的適應值情況

進化過程中的適應度函數值(平均值)變化情況如圖1所示，圖1中同時也給出與遺傳算法(GA)的對比.對于此例，采用枚舉算法求解大約需1 142 s，而提出的離散粒子群算法迭代100代所需平均時間為156.9 ms，所得最佳方案的適應度平均值為0.732，與最優值相差0.098;對遺傳算法進行同樣次數獨立實驗，每次迭代100代所需平均時間為217.3 ms，所得最佳方案的適應度平均值為1.061，與最優值相差0.427，可明顯看出離散PSO算法大大優于遺傳算法，求解精度也明顯高于文獻［8］提出的粒子群優化算法.

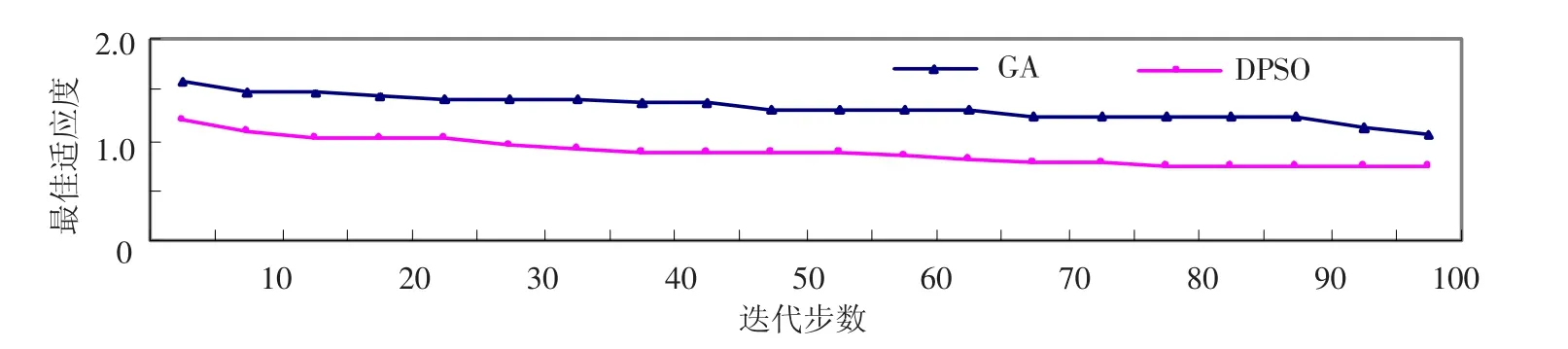
圖1 適應度函數值(平均值)變化情況

經過對大量實例的計算發現，隨著武器和目標數的增加，所提出離散粒子群算法對遺傳算法的優勢也越發明顯.圖2給出當目標數為15，武器種類數為5，且每類武器數為(4，6，5，5，4)時2種算法執行時的最佳適應度值隨時間變化情況，

此例分配方案的適應度最優值為1.404.總而言之，使用本文提出的離散粒子群優化算法能快速給出武器-目標分配問題的最優或近優解，驗證了算法的有效性.

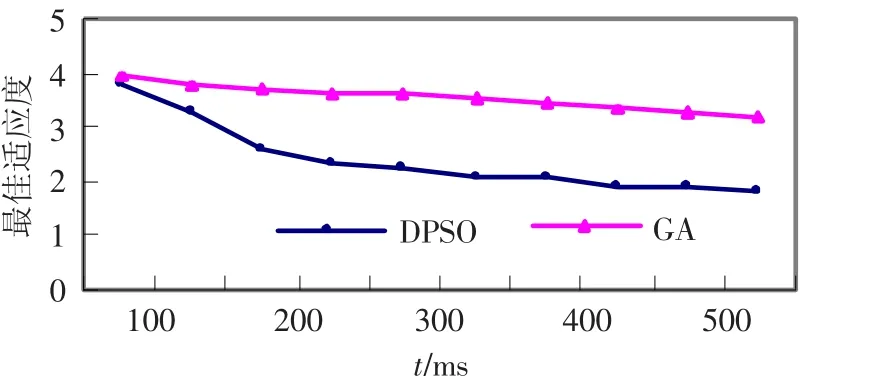
圖2 適應度函數值(平均值)隨時間變化情況

5 結論

1)采用啟發式策略對粒子群迭代過程產生的不可行解進行調節，使算法在可行解空間范圍內搜索.調節利用了貪心思想，使其有利于提高武器對目標打擊的有效性.

2)對粒子群算法中的速度和位置進行了重新定義，使粒子群算法這一主要用于連續函數優化的算法可以解決武器-目標分配問題這樣的約束組合優化問題，明顯提高了問題求解的速度和精度，拓展了粒子群優化算法在離散空間的應用.

3)提出的算法能快速給出武器-目標分配問題的最優或近優分配方案，為解決這一NP難點問題提出了新的解決途徑.

［1］AHUJA R K，KUMAR A，JHA K，et al.Exact and heuristic methods for the weapon target assignment problem［EB/OL］.(2003-06-20)［2004-04-20］http://ssrn.com/abstract=489802.

［2］ROSENBERGER J M，HWANG H S，PALLERLA R P， et al.The generalized weapon target assignment problem［C］//Proceddings of 10thInternational Command and Control Research and Technology Symposium on The Future of C2.McLean，VA:Lockheed Martin Corporation，2005:1-13.

［3］陳紹順，王穎龍，王君.多武器系統的火力分配模型［J］.火力與指揮控制，2005，30(2):45-47.

［4］鄭澤席.使用多種防空武器時目標分配的數學模型［J］.系統工程與電子技術，2000，22(5):15-16.

［5］解春明，楊傳春，李德勝.地地導彈突擊目標火力分配模型［J］.火力與指揮控制，2004，29(6):41-44.

［6］王瑋，程樹昌，張玉芝.基于遺傳算法的一類武器目標分配方法研究［J］.系統工程與電子技術，2008，30(9):1708-1711.

［7］KENNEDY J，EBERHART R C.Particle swarm optimization［C］//Proceedings of IEEE International conference on Neural Networks.Piscataway，NJ:IEEE Service Center，1995:1942-1948.

［8］高尚，楊靜宇.武器-目標分配問題的粒子群優化算法［J］.系統工程與電子技術，2005，27(7):1250-1252.