群時延內(nèi)均衡的模擬濾波器優(yōu)化設(shè)計

李 鵬,馬紅梅

(華北科技學(xué)院,北京 101601)

1 引 言

群時延是濾波器最重要的性能指標(biāo)之一,反映相位隨頻率變化的快慢,其理想狀態(tài)為一條水平直線,其值應(yīng)該是一個常數(shù)。在信號的傳輸過程中,如果群時延波動過大,會使信號產(chǎn)生畸變,對數(shù)字信號而言,因為相鄰碼元之間不同頻率分量通過群時延濾波器之后的時延不同,導(dǎo)致接收方接收到的信號會在相鄰碼元之間產(chǎn)生串?dāng)_,增加誤碼率[1]。用網(wǎng)絡(luò)綜合法設(shè)計的濾波器的群時延波動非常大,如何取得濾波器理想的帶外衰減和較小的帶內(nèi)群時延,常常是濾波器設(shè)計的難點(diǎn)[2]。一般的解決辦法是用時延均衡器來均衡。普通濾波器的群時延特性猶如鍋底狀,如果外加均衡器來“補(bǔ)平”則叫做外均衡,在濾波器內(nèi)部采用特殊措施實現(xiàn)群時延均衡的稱為內(nèi)均衡。無論是內(nèi)均衡還是外均衡,雖然能夠使群時延波動相對變小,但是時延均衡器的參數(shù)是固定的,只能被動地相對減小群時延波動,而不能從根本上解決帶內(nèi)群時延波動過大的問題。另外,加入均衡都會增加整個濾波器的元件數(shù)量,以致增大體積,加大損耗,增加成本[3]。

隨著現(xiàn)代高質(zhì)量通信系統(tǒng)的發(fā)展,不僅要求濾波器幅頻響應(yīng)滿足特定的指標(biāo),同時還要求在通帶內(nèi)具有較小的群時延特性。而相頻特性和幅頻特性之間又存在著矛盾,為使濾波器的幅頻特性和群時延特性在合理折衷的條件下各自達(dá)到最佳狀態(tài),本文提出了一種群時延內(nèi)均衡的濾波器優(yōu)化設(shè)計方法。首先根據(jù)設(shè)計指標(biāo)先對濾波器的幅頻特性進(jìn)行優(yōu)化,然后內(nèi)接時延均衡器,在通帶內(nèi)用最小二乘法擬合一條水平直線作為理想曲線的初值,然后優(yōu)化元件參數(shù),使群時延特性曲線向這條直線逼近,同時優(yōu)化整個濾波器的幅頻特性。重復(fù)上面的過程,直到獲得最佳的元件參數(shù)為止[4]。

本文中實例的幅頻特性的設(shè)計已經(jīng)發(fā)表在文獻(xiàn)[4]中,在網(wǎng)絡(luò)綜合法設(shè)計的濾波器基礎(chǔ)上,利用作者提出的極點(diǎn)放置技術(shù)和優(yōu)化技術(shù)先使濾波器的幅頻特性算術(shù)對稱[1],再內(nèi)接二階時延均衡器,最后同時優(yōu)化幅頻特性和群時延特性,降低群時延的波動。

2 時延均衡器直接耦合

利用文獻(xiàn)[4]提出的極點(diǎn)放置技術(shù)和優(yōu)化技術(shù)設(shè)計出來的濾波器雖然幅頻特性能達(dá)到算術(shù)對稱,但相頻特性很難接近線性,為解決此問題,需要在電路中加時延均衡器。一階均衡器僅有一個設(shè)計參數(shù),對群時延的均衡效果有限,所以一般都選用二階均衡器。二階均衡器有兩個設(shè)計參數(shù) Wr和Q,Wr是群時延最小值處的頻率,Q是濾波器的品質(zhì)因數(shù)。通常要根據(jù)Wr和Q來計算二階均衡器的各個元件參數(shù)。本文采用內(nèi)均衡方式直接耦合時延均衡器[5]。

3 幅頻和群時延特性模型的建立

3.1 濾波器幅頻特性目標(biāo)函數(shù)的建立

濾波器幅頻特性的數(shù)學(xué)模型在文獻(xiàn)[4]中已經(jīng)給出 ,即:

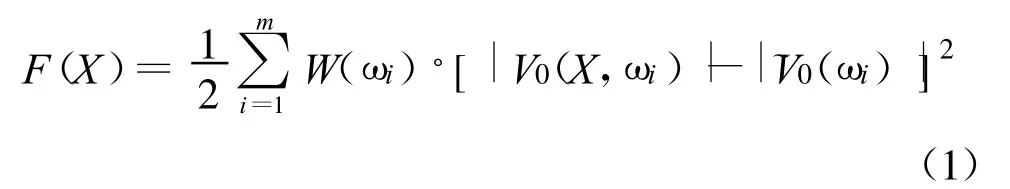
3.2 群時延特性目標(biāo)函數(shù)的建立

建立濾波器群時延特性數(shù)學(xué)模型,先在通帶內(nèi)取p個頻率點(diǎn),然后求各個頻率點(diǎn)群時延的實際值與理想值之差的平方和,目標(biāo)函數(shù)可以寫成:

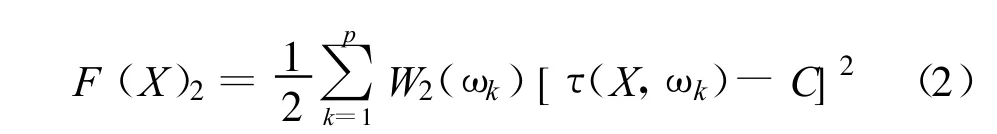
式中,W2(ωk)為各頻率點(diǎn) ω′1,ω′2,ω′k,…,ω′p上相頻特性的權(quán)重函數(shù);τ(X,ωk)為各個頻率點(diǎn)上實際的群時延值,其值可由相位求導(dǎo)得到;C為理想的群時延特性曲線,其值為一常數(shù)。

3.3 濾波器總目標(biāo)函數(shù)的建立

濾波器總的目標(biāo)函數(shù)就是幅頻特性目標(biāo)函數(shù)與群時延特性目標(biāo)函數(shù)之和,即:

4 濾波器的優(yōu)化

4.1 目標(biāo)函數(shù)的梯度

對目標(biāo)函數(shù)進(jìn)行優(yōu)化,首先要求出目標(biāo)函數(shù)的梯度。幅頻目標(biāo)函數(shù)的梯度在文獻(xiàn)[4]中已經(jīng)給出,對群時延特性的梯度,因為群時延是相位對頻率的一階導(dǎo)數(shù),為使編程方便,所以把群時延的梯度轉(zhuǎn)換為對相位的梯度,即:

式中,τp為相位延遲,φ為相位,ω為角頻率。轉(zhuǎn)換后的梯度為

4.2 優(yōu)化過程

對于群時延特性,需要將目標(biāo)函數(shù)向一個常數(shù)優(yōu)化,這個常數(shù)可以由最小二乘法求得。對總的目標(biāo)函數(shù),利用無約束最優(yōu)化方法可以使目標(biāo)最小,此時幅頻特性接近于理想狀態(tài),群時延接近于常數(shù)。

5 實例分析

以設(shè)計一個無源帶通濾波器為例,中心頻率是490MHz,3 dB帶寬為70MHz,線性坐標(biāo)下±90MHz處衰減大于55 dB,矩形系數(shù)小于2.5,群時延波動小于12 ns,兩端接電阻都是50Ψ。

6 網(wǎng)絡(luò)綜合法設(shè)計

6.1 幅頻特性設(shè)計

對濾波器幅頻特性的設(shè)計,采用六階電容耦合諧振濾波器,具體電路和參數(shù)以及幅頻特性在文獻(xiàn)[4]中已經(jīng)給出。圖1為通帶內(nèi)的群時延特性曲線。

圖1 濾波器的群時延特性Fig.1 Group-delay of the filter

6.2 時延均衡器直接耦合

從圖1可以得出,通帶內(nèi)群時延波動的最大值是35.05 ns,在峰值處的頻率為499.69 MHz,再根據(jù)二階時延均衡器的設(shè)計公式可以得出Q的大概值為[5]27.51。耦合時延均衡器后的電路如圖2所示。

圖2 時延均衡器直接耦合電路Fig.2 Filter circuit coupledwith group-delay equalizer

時延均衡器直接耦合后,幅頻特性基本保持不變,群時延特性如圖3所示。

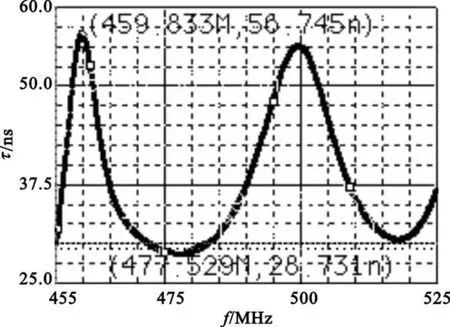
圖3 時延均衡器直接耦合后的群時延特性Fig.3 Group-delay of the filter coupled with group-delay equalizer

由仿真可以得出,在490±35 MHz處的衰減分別為10.968 dB和0.2647 dB,在 490±90MHz處的衰減分別為76.383 dB和47.698 dB,通帶內(nèi)群時延的最大波動為28.014 ns,此時濾波器的通帶偏向高頻處且不算術(shù)對稱。

7 優(yōu)化設(shè)計

7.1 幅頻特性的優(yōu)化

優(yōu)化法設(shè)計時延濾波器,首先利用極點(diǎn)放置技術(shù)對電路進(jìn)行改進(jìn),然后再對濾波器的幅頻進(jìn)行優(yōu)化。改進(jìn)后的電路及優(yōu)化后的幅頻特性參見文獻(xiàn)[4]中的圖4和圖5,群時延特性如圖4所示。

圖4 幅頻優(yōu)化后的群時延特性Fig.4 Group-delay of the filter′s amplitude-frequency optimized

7.2 時延均衡器直接耦合

從圖4可以看出,通帶內(nèi)群時延波動的最大值是23.617 ns,在峰值處的頻率為489.403MHz,再根據(jù)二階時延均衡器的設(shè)計公式可以得出 Q的大概值為18.156[5]。耦合時延均衡器后的電路和群時延特性如圖5和圖6所示,此時濾波器的幅頻特性基本不變,通帶內(nèi)群時延波動的最大值減小到16.584 ns。

圖5 改進(jìn)的時延均衡器直接耦合電路Fig.5 Improved filter circuit coupledwith group-delay equalizer

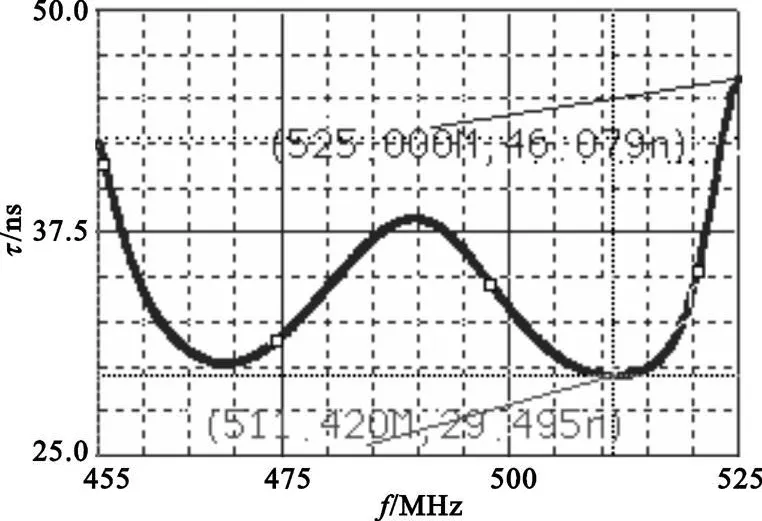
圖6 時延均衡器直接耦合后的群時延特性Fig.6 The filter′s group-delay coupled with group-delay equalizer

7.3 電路整體優(yōu)化

對整個電路的幅頻特性和群時延特性同時進(jìn)行優(yōu)化,優(yōu)化后的曲線分別如圖7和圖8所示。

圖7 優(yōu)化后的幅頻特性Fig.7 Amplitude-frequency optimized

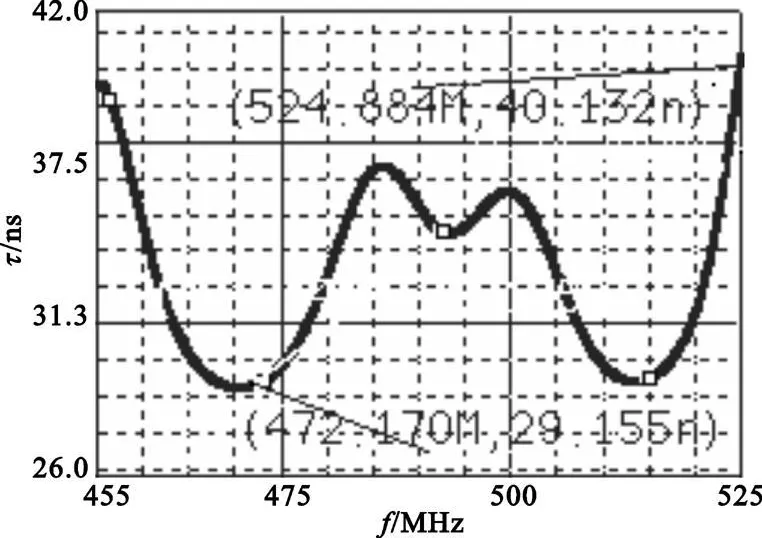
圖8 優(yōu)化后的群時延特性Fig.8 Group-delay optimized

由仿真可以得出,在490±35 MHz處的衰減分別為2.0492 dB和0.554 dB,在490±90MHz處的衰減分別為55.901 dB和60.355 dB,通帶內(nèi)群時延的最大波動為10.977 ns。

8 結(jié) 論

Pspice仿真結(jié)果表明,用網(wǎng)絡(luò)綜合法設(shè)計的內(nèi)接時延均衡器的濾波器,其通帶內(nèi)群時延最大波動為28.014 ns,幅頻特性在線性坐標(biāo)下不對稱;優(yōu)化后的幅頻特性基本上是算術(shù)對稱的,通帶內(nèi)群時延最大波動為10.977 ns,只有網(wǎng)絡(luò)綜合設(shè)計法的39.18%。設(shè)計實例表明,優(yōu)化設(shè)計方法相比于網(wǎng)絡(luò)綜合設(shè)計方法來說,不但能夠使幅頻特性和群時延特性達(dá)到合理的折衷,而且能夠解決網(wǎng)絡(luò)綜合設(shè)計方法難以實現(xiàn)的線性群時延設(shè)計問題,具有良好的工程應(yīng)用價值。

[1]王大壽,趙濤.LC濾波器的小型化制作與生產(chǎn)[J].大連海運(yùn)學(xué)院學(xué)報,1994,20(4):60-66.WANG Da-shou,ZHAO Tao.The miniaturization make of the LC filters[J].Journal of Dalian Marine College,1994,20(4):60-66.(in Chinese)

[2]江山.窄帶小群時延波動晶體濾波器設(shè)計[J].電訊技術(shù),2010,50(3):54-58.JIANG Shan.Design of Narrow band Little Ripple Group delay Crystal Filter[J].Telecommunication Engineering,2010,50(3):54-58.(in Chinese)

[3]沙海.衛(wèi)星導(dǎo)航系統(tǒng)傳輸信道的群時延測量方法研究與應(yīng)用[D].長沙:國防科技大學(xué),2009.SHA Hai.Research andApplication of the Group Delay Measurement Method in Transfer Channel of Satellite Navigation System[D].Changsha:National University of Defense Technology,2009.(in Chinese)

[4]李鵬,馬紅梅.幅頻算術(shù)對稱無源帶通濾波器的優(yōu)化設(shè)計[J].電訊技術(shù),2010,50(6):105-108.LI Peng,MA Hong-mei.Optimization Design of Amplitude-frequency Arithmetic Symmetry Passive Bandpass Filter[J].Telecommunication Engineering,2010,50(6):105-108.(in Chinese)

[5]阿瑟·B·威廉斯.電子濾波器設(shè)計手冊[M].北京:電子工業(yè)出版社,1986:201-208.Arthur B Williams.Design Handbook of Electric Filter[M].Beijing:Publishing House of Electronic Industry,1986:201-208.(in Chinese)